EXAMINAREA NEDISTRUCTIVA PRIN METODA ULTRASUNETELOR

EXAMINAREA NEDISTRUCTIVA PRIN METODA ULTRASUNETELOR

1. INTRODUCERE

Posibilitatea utilizarii undelor ultrasonice pentru testari nedistructive s-a recunooscut de abia in anii '30, in Germania de catre Mulhauser, Trost, Pohlman, iar in Rusia de catre Sokoloff, acestia folosind tehnici variate cu unde continue. Echipamentul de detectie s-a dezvoltat bazandu-se pe principiul interceptarii energiei ultrasonice de catre o discontinuitate aflata in calea fascicolului ultrasonic. Aceasta tehnica a fost cunoscuta mai tarziu sub denumirea de metoda prin transmisie. Un sistem ingenios de transmisie a fost dezvoltat de catre Pohlman. Acesta se baza pe producerea de imagini ca niste umbre ale defectelor interne. Mai tarziu s-au perfectionat cateva tipuri de astfel de detectori. In timpul perioadei de inceput examinarea cu ultrasunete era destul de limitata deoarece metoda prin transmisie necesita accesul la ambele fete ale materialului testat. Nu a fost gasita o practica mai buna pana cand Firestone a inventat aparatul ce utilizeaza trenul de pulsuri ultrasonice, obtinand reflexii de la discontinuitatile din materialul testat. Acest aparat, pe care el l-a numit "reflectoscopul ultrasonic" s-a dezvoltat rapid datorita perfectionarii instrumentatiei ultrasonice. In anii '40 acest aparat era un lider al aparatelor ultrasonice de detectie a defectelor, atat in Statele Unite ale Americii cat si in afara acestora. In aceasi perioada, echipamentul de testare ultrasonica a fost dezvoltat independent de catre Sproule, in Anglia.

Aplicatii ale acestei metode au aparut in scurt timp, in productie inspectia ultrasonica fiind aplicata in cadrul examinarii calitative in metalurgie. Cercetarile au continuat, Firestone fiind din nou cel care a adus majoritatea contributiilor importante impreuna cu asociatii sai de la Universitatea Michigan, ei preocupandu-se de investigarea mecanismului de functionare al traducatorilor, posibilitatea utilizarii undelor de forfecare, aplicatiile Rayleigh, ale undelor Lamb, metoda rezonantei pentru masuratori de grosime etc.

Deoarece metoda ultrasonica este bazata pe fenomene mecanice, in particular ea este adaptata determinarii structurii materialelor tehnice. Principalele aplicatii ale acestei metode sunt: determinarea discontinuitatilor, masurarea grosimilor, determinarea modului de elasticitate, studiul structurii metalurgice. Avantajele acestei metode sunt urmatoarele: sensibilitatea mare de detectie, putere de penetrare mare (permitand examinarea unor grosimi foarte mari), acuratete in determinarea pozitiei discontinuitatii si estimarea marimii acesteia, raspuns rapid, metoda pretandu-se la automatizare, accesul numai dintr-o singura parte a materailului testat.

Metoda ultrasonica are totusi limitari cum ar fi: geometria nefavorabila a produsului testat(marime, contur, complexitate si orientare a discontinuitatilor), structura interna nefavorabila (granulatie mare, porozitati structurale, incluziuni etc).

In zilele noastre examinarea cu ultrasunete acopera un domeniu foarte larg de investigare, cum ar fi: industria metalurgica, energetica, aeronautica, constructoare de masini, constructii transporturi etc.

2. OSCILATII SI UNDE

Oscilatiile elastice sau vibratiile elastice reprezinta variatii periodice de stare a mediului. Pentru propagarea oscilatiilor este necesara prezenta unui mediu material, adica prezenta legaturilor elastice intre particulele substantei. La trecerea undei prin mediu particulele se abat intr-un mod anumit de la pozitia de echilibru. Daca una din particule este abatuta din pozitia de echilibru, atunci actiunea fortelor elastice din partea celorlalte particule tinde s-o readuca in starea initiala: prezenta fortelor elastice conduce la faptul ca potiunile vecine se manifesta ca fiind scoase din pozitia de echilibru, iar prezenta fortelor de inertie este cauza faptului ca particulele continua sa oscileze in jurul unei pozitii medii chiar si dupa trecerea undei.

Urechea omului receptioneaza in mod normal, oscilatii elastice de frecventa joasa si anume de la 16 la 16000 oscilatii pe secunda. Cand frecventa oscilatiilor particulelor mediului se afla intre aceste limite atunci undele elastice sunt receptionate de om sub forma sunetului. Cand frecventa oscilatiilor particulelor mediului depaseste pragul superior, atunci aceste oscilatii se numesc ultrasonice sau ultrasonore. Limita superioara de frecventa a oscilatiilor ultrasonice este de aproximativ 10¹⁰ oscilatii pe secunda, frecventa ce corespunde oscilatiilor termice ale moleculelor in corpurile solide.

2.1. OSCILATIA SISTEMELOR ELASTICE. OSCILATII LIBERE

Oscilatiile elastice in toate gamele de frecventa, din punct de vedere fizic sunt echivalente intre ele. Propagarea lor se supune acelorlasi legi acustice.

Intervalul de timp intre 2 stari similare de miscare a corpului in oscilatie se numeste perioada de oscilatie T, iar numarul de oscilatii care se executa in unitatea de timp se numeste frecventa f.

Frecventa si perioada sunt legate prin relatia:

f = 1/T = w p (3.1)

Marimea w se numeste pulsatie sau frecventa circulara si reprezinta numarul de oscilatii complete care se efectueaza in 2p unitati de timp. Daca timpul se masoara in secunde, atunci unitatea de frecventa este frecventa acelei oscilatii a carei perioada este egala cu o secunda. Aceasta unitate de frecventa se numeste Hertz.

In orice moment corpul oscilant poseda o valoare bine determinata pentru deplasare, vitezaq si acceleratie. Fie momentul de timp t = 0, acel moment la care corpul a fost scos din pozitia de echilibru si a inceput sa oscileze. Atunci la momentul de timp t valoarea instantanee a deplasarii (elongatiei) va fi egala cu:

x = A sin wt = A sin 2p ft, (3.2)

unde A este amplitudinea oscilatiei.

Expresia de mai sus reprezinta ecuatia miscarii armonice oscilatorii. Viteza punctului material oscilator sau viteza de deplasare instantanee este egala cu derivata deplasarii in functie de timp adica:

n = dx/dt = A cos wt    (3.3)

Valoarea maxima a vitezei de oscilatie are loc pentru cos wt = 1

n_m wA = 2pA    (3.4)

Derivand fata de t relatia ce defineste viteza se obtine expresia pentru acceleratia punctului material oscilant:

a= d_n/dt = - A w sin wt.    (3.5)

Valoarea maxima a acceleratiei este:

a _m = A w wn_m. (3.6)

Din formulele ce contin definitia vitezei si acceleratiei punctului care executa o miscare oscilatorie armonica se observa ca acestea sunt functii periodice de timp avand aceiasi perioada T; viteza creste proportional cu frecventa iar acceleratia creste cu patratul frecventei.

Dupa cum se stie, orice miscare oscilatorie este o miscare care se desfasoara cu acceleratie. De aceea asupra corpurilor oscilante trebuie sa actioneze forte care sa le imprime aceste acceleratii. In particular, daca un corp de masa m, de exemplu o bila suspendata de un resort, este scos din pozitia de echilibru, atunci fortele de elasticitate ce actioneaza in resort vor readuce aceast corp in pozitia de echilibru si bila va incepe sa efectueze o oscilatie armonica. Conform celei de a doua legi a mecanicii asupra masei m va actiona o forta egala cu:

F = m a_m = -m w x = - kx (3.7)

Unde k m w este coeficientul de rigiditate al resortului (sistemului oscilant).

In aceste fel asa cum rezulta din expresia anterioara, pentru ca corpul sa efectueze o miscare oscilatorie armonica asupra lui trebuie sa actioneze cu o forta indreptata intotdeauna spre pozitia de echilibru, iar ca marime trebuie sa fie direct proportionala cu deplasarea din aceasta pozitie.

Ne propunem sa definim legea miscarii oscilatorii. Sa presupunem o masa oarecare m concentrata intr-un volum foarte mic care efectueaza o oscilatie armonica. Energia totala a unui astfel de sistem mecanic se compune din energia cinetica si potentiala in procesul de oscilatie, marimea lor variind periodic.

Energia cinetica a sistemului are expresia:

E_c=mn m w A²sin² wt/2.    (3.8)

Energia potentiala a sistemului asupra caruia actioneaza forta de tip F=kx este:

E_p=kx²/2= m w A² sin² wt/2.s

Energia totala va fi:

E_t = E_c + E_p = m w A²/2    (3.10)

Din expresia de mai sus rezulta ca energia totala a miscarii armonice oscilatorii este direct proportionala cu patratul amplitudinii si cu patratul frecventei circulare a oscilatiilor.

Sa examinam prin ce ecuatii diferentiale se poate descrie miscare oscilatorie armonica. Fie masa m, exemplu o bila suspendata de un resort, care efectueaza oscilatii armonice proprii. In absenta fortelor de frecare, oscilatiile armonice vor continua infinit de mult deoarece energia totala a unui sistem inchis este o constanta. Asupra bilei scoase din pozitia de echilibru actioneaza forta de sens invers - kx, cu ajutorul careia bila se va putea deplasa spre pozitia de echilibru. Insa in pozitia de echilibru bila nu se va opri intrucat asupra ei actioneaza forta de inertie egala cu md²x/dt² care provoaca abaterea bilei in sensul invers pozitiei de echilibru. Ecuatia de miscare a bilei de masa m va avea aspectul:

m(d²x/dt²) = -kx sau m(d²x/dt²) + kx = 0 (3.11)

Tinand seama de notatia lui k, expresia anterioara se va scrie:

m(d²x/dt²) + w x = 0    (3.12)

Daca sistemul oscilatoriu se afla intr-un mediu oarecare atunci energia sa se consuma prin invingerea fortelor de frecare, prin aceasta amplitudinea si viteza miscarii oscilatorii scad treptat. Astfel de oscilatii se numesc amortizate. Legea variatei amplitudinii oscilatiilor amortizate depinde de mmarimea si caracterul fortelor de rezistenta care la randul lor depind de proprietatilde mediului. In acest caz, cea de a doua lege a dinamicii pentru sisteme oscilatorii se scrie:

m(d²x/dt²) = kx - r(d²x/dt²), (3.13)

unde r este un factor de proportionalitate pentru rezistenta mecanica a mediului.

Expresia de mai sus este valabila pentru cazul oscilatiilor mici, pentru care viteza corpului este mica si forte de rezistenta este proportionala cu viteza.

Sa impartim expresia la masa corpului si sa notam:

r/m = 2d si w = (k/m)^1/2

atunci obtinem o ecuatie diferentiala pentru oscilatiile amortizate:

d²x/dt² + 2d(dx/dt) + w²x = 0    (3.14)

Solutia acestei ecuatii, in conditia cand w >d este reprezentata de expresia:

x = A_oe^-dt sin w't,

unde w w d (3.15)

Amplitudinea oscilatiilor se schimba in decursul timpului dupa o lege exponentiala:

A = A_oe^-dt (3.16)

Marimea d defineste viteza descresterii amplitudinii oscilatiilor in timp si este denumita coeficient de amortizare.

Sa calculam raportul amplitudinilor invecinate una de alta cu o perioada:

A_n/A_n+1 = A_oe^-dt/ A_oe^-d(t+T) = e^dt (3.17)

Logaritmul natural al relatiei de mai sus este denumit decrement logaritmic al amortizarii:

D = ln A_n/A_n+1 = ln e^-dt dT    (3.18)

sau:

D = (r/2m)T    (3.19)

Decrementul logaritmic al amortizarii este direct proportional cu marimea coeficientului de amortizare si invers proportional cu masa intregului sistem.

3.1.2. TIPURI DE UNDE

Undele acustice pot fi de diverse tipuri in raport cu traiectoria pe care o pot avea particulele mediului si cu natura si dimensiunea corpului prin care se propaga undele.

In cazul cand traiectoria este liniara si deplasarea particulelor se produce in directia propagarii undelor, undele se numesc longitudinale. Propagarea unei unde longitudinale printr-un mediu va produce compresii si decompresii. In general, propagarea undelor longitudinale este legata de variatii periodice locale de presiune, de densitate si de volum specific. Undele longitudinale se propaga in medii solide, lichide si gazoase.

Daca dimensiunile corpului solid nu pot considerate infinite si devin comparabile cu lungimea undei acustice, se produce o schimbare a volumului corpului prin care se propaga undele, undele numindu-se in acest caz cvasilongitudinale.

Cand traiectoria particulelor este tot liniara, insa deplasarea particulelor se face intr-o directie perpendiculara pe directia propagarii undelor, acestea se numesc transversale.

Daca corpul solid are dimensiuni finite - o bara sau o placa a caror raza, respectiv grosime, sunt comparabile cu lungimea undei - in loc de unde transversalele apar unde de incovoiere.

In cazul cand traiectoria este un cerc cu centrul in pozitia de repaus a particulei sau o elipsa continuta intr-un plan paralel cu directia de propagare a undelor, acestea se numesc unde de suprafata sau unde Rayleigh. Acest tip de unde se intalnesc in semispatii lichide sau solide la suprafata de separare a unor asemenea medii in contact cu vidul sau cu un mediu suficient de rarefiat, de exemplu, aerul. Aceste unde se propaga pe o adancime de cateva lungimi de unda si numai la suprafata corpului. Undele Rayleigh se propaga si dupa muchiile corpului investigat ceea ce le face utile in depistarea ultrasonica a fisurilor si defectelor de suprafata.

Daca traiectoria particulei este tot circulara, insa planul circular este perpendicular pe directia de propagare a undelor, acestea se numesc unde de torsiune. Acest tip de unde se intalnesc in cadrul barelor circulare sau a tuburilor supuse actiunii unor cupluri.

Existenta undelor de suprata implica o anumita grosime a corpului solid, acestea trebuind sa fie mai mari decat lungimea de unda. Sunt cazuri insa, cand grosimea unei placi este egala sau mai mica decat lungimea de unda. In aceasta situatie nu se mai produc unde de suprafata pure, ci o varianta a acestora, cunoscute sub denumirea de unde de placa. Directia de propagare a undei de placa este paralela cu suprafata placii si intreaga sectiune a placii ia parte la miscarea de oscilatie, deci la transportarea energiei.

Daca perturbatia este produsa de un punct material aflat in oscilatie (sursa punctuala), fronturile undei sunt suprafete sferice, avand centrul intr-un punct care coincide cu sursa. Acestea sunt undele sferice.

Undele Lamb sunt unde care apar atunci cand oscilatiile elastice sunt generate in placi subtiri sau in tevi cu pereti subtiri, particulele mediului efectuand in acest caz miscari eliptice intr-un plan perpendicular pe directia de propagare a frontului de unde. Undele Lamb pot fi de 2 tipuri: simetrice sau de dilatare si nesimetrice sau de incovoiere.

Undele Lamb pot fi excitate prin incidenta oblica a unei unde longitudinale pe suprafata corpului investigat. Amplitudinea va fi maxima atunci cand viteza de faza a undei longitudinale va fi egala cu viteza de faza a undei Lamb, atunci cand este satisfacuta conditia:

sin a = V_L/V_P

sau:

V_P = vl /sin a

Unde: a - unghiul de incidenta al undelor longitudinale;

v - frecventa undelor longitudinale;

l - lungimea de unda a undelor longitudinale;

V_p - viteza de faza a undei Lamb;

V_L - viteza de faza a undelor longitudinale.

Pe langa dependenta de v si l a undei longitudinale, lungimea de unda Lamb depinde si de grosimea placii in care se produce aceasta.

3.1.3. ECUATIA UNDELOR

Analizam cum are loc propagarea oscilatiilor in mediu si in ce fel se poate caracteriza analitic un proces ondulatoriu.

Fie un punct material care efectueaza o oscilatie intr-un mediu, in care toate particulele sunt legate intre ele. Oscilatia punctului material creeaza in mediul inconjurator tensiuni elastice, care la randul lor provoaca oscilatia particulelor invecinate, transmitand in continuare oscilatia mai departe (particulelor inconjuratoare) etc. Fenomenul de propagare a oscilatiilor in mediu il numim unda.

La propagarea undei nu are loc o transmisie de substanta intrucat pozitia de echilibru in jurul careia se efectueaza oscilatia particulelor mediului nu se deplaseaza.

Sa admitem ca undele se propaga in lungul axei OY, adica in sensul cresterii valorii coordonatei y.

Sa notam prin x deplasarea punctului din pozitia de echilibru. Procesul ondulatoriu va fi cunoscut daca se cunoaste deplasarea lui x in fiecare moment al timpului pentru fiecare punct al dreptei in lungul careia se propaga unda, adica, daca se stie deplasarea punctului x ca functie de timp si de coordonata a pozitiei de echilibru a punctelor.

Drept origine a coordonatei O, alegem acel punct de pe dreapta care este centrul deplasarilor si care oscileaza dupa legea:

x = A sin wt    (3.20)

Pe dreapta OY luam punctul arbitrar O' dispus la distanta y de O.Oscilatia ajunge pana la punctul O' in intervalul de timp:

t = y/c

Punctul O' incepe sa se deplaseze in timpul t' fata de punctul O (pozitia de echilibru), iar deplasarea x a punctului O' se va exprima prin:

x = A sin wt ₁,    (3.22)

unde t ₁ este timpul calculat din momentul cand punctul A a inceput sa oscileze. Deoarece t₁ = t - t' ,ecuatia anterioara capata aspectul:

x = A sin w(t - t') (3.23)

sau:

x = A sin w(t - y/c) (3.24)

Ultima ecuatie defineste deplasarea x ca o functie de timpul t si de distenta y a punctului O' fata de centrul de oscilatie O. Ea reprezinta ecuatia undei care s-a propagat in lungul dreptei OO'.

Sa admitem ca unda se propaga in sens invers adica de la punctul O' spre O, in sensul descresterii coordonatei y. Atunci in ecuatia anterioara y trebuie sa fie inlocuit cu -y, iar ecuatia unei astfel de unde se va scrie sub forma:

x = A sin w(t + y/c) (3.25)

La deducerea formulei s-a presupus ca amplitudinea de oscilatie, A, pe masura propagarii undei, nu variaza, iar viteza de propagare a fazei oscilatorii este aceeasi.

Intr-un mediu elastic sunt posibile unde de un alt tip decat cele plane, de exemplu sferice sau cilindrice.

Intr-o unda sferica amplitudinea oscilatiei se micsoreaza invers proportional cu distanta R fata de sursa de oscilatie. Ecuatia undei sferice are aspectul:

x = A/R sin w(t - R/c)    (3.26)

Suprafetele de unda (suprafetele fazelor egale) a unei astfel de unde sunt sferele.

Pentru unde cilindrice amplitudinea oscilatiilor se micsoreaza invers proportional cu (R)^1/2 ,

x = A/(R)^1/2 sin w(t - R/c)    (3.27)

Suprafetele de unda ale undei cilindrice sunt niste cilindri concentrici .

Eliminand in ecuatia (3.24) timpul, obtinem:

x = A sin (w y/c)    (3.28)

care defineste un proces periodic fata de directia de propagare y. Doua puncte separate unul de altul de o distanta egala cu l au aceasi faza de oscilatie si sunt legate prin relatia:

w(y + l)/c - w (y/c) = 2p (3.29)

De aici, luand in considerare ca w pf , gasim:

l = c sau l = c/ = cT (3.30)

Marimea l este lungimea de unde. In acest fel, folosind formula de mai sus, expresia (3.24) devine:

x = A sin[2p(ft - (y/l))] = A sin [2p l(ct - y)]    (3.31)

Propagarea procesului ondulatoriu se poate descrie printr-o ecuatie de propagare care este o ecuatie diferentiala cu derivate partiale. Pentru deducerea ecuatiei ondulatorii folosim ecuatia undei plane (3.24).

Sa derivam partial marimea oscilatorie x in raport cu timpul, y fiind constant:

n x/ t) = Aw cos(t - y/c)

(3.32)

a x/ t² = - Aw sin w(t - y/c)

Daca x inseamna deplasarea particulelor mediului in decursul osculatiilor atunci n si a vor fi viteza si acceleratia acestor particule in cazul miscarii lor oscilatorii in punctul de coordonate y.

Derivatele partiale ale lui x fata de y, pastrand t constant, vor fi egale cu:

x/ t = A(w/c)cos w(t - (y/c)) (3.33)

x/ y² = (w /c²)sin w(t - (y/c))

Comparand ultima expresie cu cea a acceleratiei obtinem:

x/ t² = c²( x/ y²)    (3.34)

Aceasta ecuatie reprezinta ecuatia diferentiala a unei unde plane care se propaga pe axa OY cu viteza c intr-un mediu liniar, izotrop, omogen, conservativ ( in alte cazuri ecuatia de propagare este cea mai complicata); aceasta ecuatie se numeste ecuatie se numeste ecuatia de propagare a undelor. Ecuatia poate fi folosita pentru determinarea vitezei sunetului in diferite medii.

3.1.4. PRESIUNEA UNDELOR

Cunoscand viteza de oscilatie si acceleratia particulelor mediului la propagarea undei, se poate determina valoarea presiuniivariabile care apare in mediu la propagarea undei acustice.

Presiunea instantanee in unda plana se obtine din ecuatia de miscare a lui Newton avand aspectul:

-d_p/d_y = - rwA sin(t - y/c)    (3.35)

Integrand aceasta expresie fata de y aflam dependenta presiunii de coordonate si timp:

p_t = p₀ + rwA cosw(t - y/c) = p₀ - p    (3.36)

In care p_t este presiunea totala iar p_o presiunea statica

Expresia:

p = rwcA cosw(t - y/c)    (3.37)

Reprezinta o presiune provocata de unda, iar:

p_m = rwcA = n_mrc    (3.38)

Este amplitudinea presiunii acustice (presiunea acustica mixta).

Perturbatia provocata de punctul material in oscilatie se propaga prin mediul elastic sub forma de compresiuni si rarefieri. Intrucat compresiunea se datoreaza unei mariri a presiunii iar rarefierea unei micsorari a presiunii, propagarea undelor acustice se asimileaza cu o variatie a presiunii, propagarea undelor acustice se asimileaza cu o variatie a presiunii in timp si spatiu. Considerand un punct anumit in campul acustic, presiunea acustica instantanee reprezinta presiunea totala la un moment dat din care se scade presiunea statica in acel punct. Cand mediul elastic de propagare a undelor este atmosfera, presiunea statica este echivalenta cu cea atmosferica.

Spre deosebire de presiunea acustica instantanee, care este o marime variabila in timp,forta exercitata asupra unei suprafete prin incidenta unui fascicul de unde cu o suprafata este constanta; aceasta se numeste presiune de radiatie acustica. Aceasta forta depinde de intensitatea undelor, de proprietatile elastice ale mediului, de orientarea suprafetei mediului fata de directia de propagare a fasciculului, precum si de aria acestei suprafete.

Valoarea presiunii de radiatie acustica se poate determina prin formula:

p_r = rn m/2    (3.39)

Sau pentru cazul particular al undelor plane:

p_r = I/c    (3.40)

Unde I este intensitatea undelor acustice.

3.1.5. MARIMI ACUSTICE

a)Impedanta acustica

Marimea definita de raportul:

Z = p/v    (3.41)

Se numeste impedanta acustica specifica.

Aceasta este o marime complexa deoarece presiunea acustica, in general, nu este in faza cu viteza particulei, Doar in cazul particular al undelor progresive, care se propaga intr-un mediu nelimitat, fara pierderi de energie, presiunea acustica si viteza particulei gasindu-se in faza, impedanta acustica specifica este o marime reala. In acest caz ea devine egala cu produsul dintre densitatea mediului si viteza de propagare a undei acustice prin acel mediu, adica:

z = rc (3.42)

Cum aceasta marime depinde de caracteristicile fizice ale mediului, produsul rc se mai numeste impedanta caracteristica a mediului

b)Energia acustica.

Energia portiunii din mediul in care se propaga unda se compune din energie cinetica E_c si energie potentiala E_p.

Notand volumul portiunii mediului cu V, masa lui cu m, viteza de deplasare a particulelor mediului cu v, energia cinetica a volumului mediului considerat este:

E_c = mv²/2    (3.43)

Avand in vedere m = rV si tinand cont de expresia acceleratiei obtinem:

E_c= 1/2rVA²w sin² w(t - (y/c))     (3.44)

Energia potentiala a portiunii mediului cu volumul V , supus deformarii relative dx/dy, este:

E_p = 1/2k(dx/dy)²V (3.45)

Unde dx este diferenta deplasarii particulelor mediului care sunt situate una fata de alta la distanta dy iar k este compresivitatea mediului.

Substituind expresia deformarii relative din formula:

x/ y²=Aw /c²sinw(t-(y/c))    (3.46)

In expresia energiei potentiale, obtinem:

E_p = 1/2k Aw /c² Vsin²(t-(y/c)) (3.47)

Din comparatie expresiilor energiilor cinetice si potentiale exprimate anterior rezulta ca energia cinetica ci cea potentiala variaza in aceasi faza, adica in acelasi timp ajung la valorile maxime si minime. In aceasta consta principala deosebire a energiei de oscilatie a unui punct material izolat valoarea energiei totale ramane constanta, in timp ce la progarea undelor in mediu, energia totala a portiunii mediului in care se propaga unda variaza odata cu transferul energiei dintr-o portiune a mediului in alta.

Adunand expresiile celor doua energii se aflaenergia totala a elementului de volum al mediului

E_t= ½((1/kc²)+r)A²w Vsin²(t-(y/c))    (3.48)

Deoarece viteza de propagare a undelor longitudinale in bare solide se defineste:

c = (E/r)^1/2= (1/kr (3.49)

Si expresia energiei totale devine:

E_t= rA²w Vsin²w(t-(y/c))    (3.50)

Intrucat valoarea medie a patratului sinusului intr-o perioada este egala cu ½, valoarea medie totala a energiei volumului mediului este:

t E/V = 1/2rA²w (3.51)

Rezulta ca densitatea de energie este proportionala cu densitatea mediului, cu patratul amplitudinii si cu patratul frecventei.

c) Intensitatea undelor acustice.

Avand in vedere ca energia nu ramane in portiunea respectiva ci se transfera in mediu, se introduce notiunea de intensitate a undelor acustice. Intensitatea acustica reprezinta fluxul de energie acustica care strabate unitatea de suprafat perpendiculara pe directia de propagare a undelor.

Intrucat energia se propaga cu viteza sunetului, intensitatea este egala cu energia cuprinsa in paralelipipedul drept a carui suprafata a bazei este egala cu viteza sunetului c,adica:

I = tc = 1/2rcA²w (3.52)

Din expresia anterioara rezulta ca valorile maxime ale amplitudinii oscilatiei deci si a vitezei de oscilatie si acceleratiei particulelor mediului in care se propaga unda, depind de intensitatea sunetului si se determina din formulele:

A= 1/2pf(2I/rc)^1/2,

n_m = (2I/rc)^1/2,    (3.53)

a = pf(2I/rc)^1/2

Intensitatea este legata direct de puterea sursei de oscilatii N' , prin care intelegem marimea energiei totale radiata de sursa in unitate de timp. Integrand intensitatea I pe suprafata inchisa care contine sursa de oscilatii se obtine puterea acustica:

N = ò IdS_i    (3.54)

Pentru fasciculul ultrasonic plan,cu o sectiune transversala S, in conditia cand intensitatea este distribuita uniform pe toata suprafata, puterea este:

N = IS_i    (3.55)

Intensitatea acustica mai poate fi determinata daca se cunoaste marimea amplitudinii presiunii acustice cu formula:

I = p²m/2rc    (3.56)

Marimea I are o anumita directie care corespunde cu directia de deplasare a undei. Pentru unde sferice care se propaga de la o sursa punctiforma, intensitatea acustica este invers proportionala cu patratul distantei de la sursa:

I = N'/4pR²    (3.57)

Acest raport este real in cazul lipsei de atenuare in mediu, adica atunci cand energia ondulatorie nu trece in alt tip de energie. In realitate, in orice mediu, din cauza frecarilor interne si a schimbului de caldura, o parte din energia miscarii ondulatorii se consuma, de aceea cantitatea totala de energie purtata de unda depinde de distanta pana la sursa; cu cat suprafata ondulatorie considerata este mai departe de sursa cu atat energia este mai mica. Intrucat energia este proportionala cu patratul amplitudinii , amplitudinea oscilatiei se micsoreaza pe masura propagarii undei.

3.2. COMPORTAREA ULTRASUNETELOR IN MEDII DIFERITE SI LA SUPRAFATA DE SEPARARE A ACESTORA

3.2.1.ABSORBTIA ENERGIEI UNDELOR ULTRASONICE

La propagarea energiei undelor ultrasonice intr-un mediu omogen, se petrece o amortizare treptata a lor, adica micsorarea energiei undelor. Micsorarea amplitudinii oscilatiilor, deci si a intensitatii lor, odata cu indepartarea de sursa de oscilatie, este provocata de prezenta frecarii interne in mediu si de conductivitatea sa termica.

Absorbtia undelor ultrasonice plane se defineste prin urmatoarea formula:

I = I₀ e^-2ay (3.58)

Avand in vedere ca intensitatea acustica este legata de amplitudinea oscilatiei prin relatia:

I = ½ rcA²w (3.59)

Impartind ambii termeni ai acestei relatii cu 1/2rcw extragand radicalul si folosind relatia absorbtiei undelor ultrasonice obtinem:

A = A₀e^-ay

Aceasta expresie se mai poate obtine daca se face ipoteza ca la traversarea unui strat de grosime dy micsorarea relativa a amplitudinii -dA/A este proportionala cu dy, adica: -dA/A = ady unde a este o marime constanta care depinde de natura mediului fiind denumita coeficient de absorbtie acustica. Astfel, expresia precedenta se mai poate scrie:

d(ln A) = - d(ay) (3.61)

Daca diferentialele a doua marimi sunt eale, atunci insasi marimile difera una de alta printr-o constanta arbitrara de marime C, de unde:

ln A = -ax + C    (3.62)

Constanta C se determina din conditia pentru care la y = 0 marimea lui A sa fie egala cu C, deci:

ln A = ln A₀ - ay    (3.63)

Dupa care:

A = A₀e^-ay (3.64)

Conform acestei expresii amplitudinea A scade pe masura ce unda se propaga in directia axei y. Din ecuatiile ce exprima intensitatea undei ultrasonice se afla usor valorile coeficientului de absorbtie:

a hw rc³) = 8p h rc³)    (3.65)

Absorbtia energiei ultrasonice depinde de asemenea de conductivitatea termica a mediului in care se propaga unda. Astfel datorita conductivitatii termice are loc un schimb de caldura intre portiunile de compresiune si destindere din unda, care conduce la micsorarea energiei undei. Kirchoff a aratat ca in acest caz coeficientul de absorbtie este:

a p rc³)((x - 1)/C_p)k_t    (3.66)

Unde c = C_p/C_v este raportul caldurilor specifice la presiunea constanta C_p si la volum constant C_v; k_t este coeficientul de conductivitate termica.

Teoria absorbtiei energiei undelor acustice a lui Stokes si Kirchoff a fost numita teria clasica; conform acestei teorii coeficientul total de absorbtie este:

a a a p rc³))(4/3h c - 1)/C_p)k_t)    (3.67)

La studierea absorbtiei undelor acustice in lichide, de obicei se neglijeaza influenta conductivitatii termice, deoarece pentru majoritatea lichidelor, absorbtia pe seama conductivitatii termice este foarte mica. In gaze absorbtia datorata conductivitatii termice, are aceasi influenta ca absorbtia datorita vascozitatii. In corpurile solide, absorbtia energiei undelor este de asemenea legata de frecarile interne si de conductivitatea termica, in plus un rol foarte important il au histerezisul, curgerea plastica si procesele elastice de relaxare.

Bergman a efectuat experiente privind determinarea absorbtiei undelor acustice in solide, lichide si gaze, rezultatele obtinute nefiind intotdeauna corespunzatoare cu calculele teoretice.

In prezent exista multe cercetari si aplicatii care confirma teoria clasica a lui Stokes - Kirchoff pentru majoritatea lichidelor, insa pentru unele lichide cum ar fi hidrocarburi aromatice, acetati etc., teorie nu este conforma cu rezultatele practice. Aceasta permite considerarea teoriei Stokes - Kirchoff ca un caz particular al unei teorii mai generale, teoria cinetico moleculara de absorbtie a undelor acustice in lichide. Aceasta teorie a primit denumirea de teorie de relaxare, la baza ei stand presupunerea aparitiei in lichide si gaze a unor procese de relaxare a caror prezenta duce la o absorbtie suplimentara de energie acustica.

3.2.2. REFLEXIA SI REFRACTIA UNDELOR PLANE SUB INCIDENTA NORMALA

Ajungand la suprafata de separare a doua medii o unda acustica sufera o reflexie si anume o parte din energia acustica incidenta este redata primului mediu si o refractie, cealalta parte din energia acustica fiind transmisa in cel de-al doilea mediu. Astfel se produce o unda reflectata si o unda transmisa (fig.3.1.)

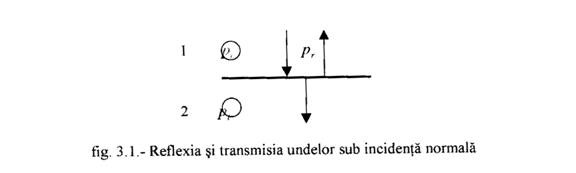
Admitand ca nu exista pierderi de energie si ca forma undelor este sinusoidala presiunea acustica este:

p_i = P_i sin(wt - k₁x)

p_r = P_r sin(wt - k₁x)    (3.68)

p_tr = P_tr sin(wt - k₂x)   

Unde k₁ si k₂ sunt numerele de unda pentru cele doua medii (k_n = 2p l

Din legea continuitatii presiunii si vitezei de oscilatie a particulelor in cele 2 medii rezulta:

p_i - p _r = p_tr    (3.69)

v_i - v_r = v_tr

In conditiile cand impedantele celor 2 medii sunt r c₁, r c₂ avem:

p_i = n_ir c₁

p_r = n_rr c₁    (3.70)

p_tr = n_trr c₂

Punand conditia x = 0 respectiv considerand ca sunt indeplinite conditiile de continuitate in punctul x = 0, relatiile presiunilor acustice devin:

P_i - P_r = P_tr (3.71)

Respectiv:

r c₂(P_i - P_r) = r c₁P_tr    (3.72)

de unde:

P_r = P_i ((r c₂ - r c₁)/ (r c₂ + r c₁))     (3.73)

Si:

P_tr = P_i ((2r c₂ )/ (r c₂ + r c₁))    (3.74)

Raportul ce exprima presiunea reflectata poate fi pozitiv sau negativ functie de calorile impedantele celor celor doua medii. Definim prin raportul P_r/P_i = R_a, factorul de reflexie acustica

R_a = (r c₂ - r c₁)/ (r c₂ + r c₁)    (3.75)

Iar prin raportul P_tr/P_i = T_a, factorul de transmisie acustica:

T_a = (2r c₂)/ (r c₂ + r c₁) (3.76)
Daca in locul presiunilor consideram intensitatile acustice cele doua relatii de mai sus devin:

K_r = I_r/I_i = ((r c₂ - r c₁)/ (r c₂ + r c₁))² (3.77)

In care K este coeficientul de reflexie acustica si:

K_tr = I_tr/I_i = (4r c₁r c₂)/ (r c₂ + r c₁)²    (3.78)

K_tr fiind coeficientul de transmisie acustica.

Asa cum se vede din expresiile celor doi coeficienti, intre ei exista relatie:

K_tr = 1 - K_r    (3.79)

In tabelul urmator de dau valorile K_r si K_tr pentru diferite medii.

De remarcat, ca in cazul unor impedante egale ale celor doua medii, factorul de reflexie cat si coeficientul de reflexie acustica devin egali cu zero, deci intreaga energie acustica trece din primul mediu in cel de-al doilea.

Tabelul 3.1. Valorile coeficientilor de reflexie si transmisie acustica pentru unele medii in contact.

3.2.3.REFLEXIA SI REFRACTIA UNDELOR SUB INCIDENTA OBLICA

In cazul cand fasciculul de unde longitudinale plane intalneste planul de separare a doua medii sub un unghi do incidenta q_{i ,} o parte din energia acustica este reflectata in directia OR sub unghiul q, iar cealalta parte este transmisa in cel de al doilea mediu in directia OT sub unghiul q_tr

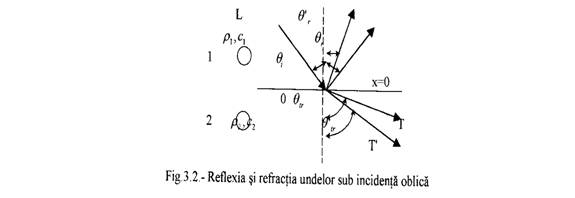
Deoarrece presiunea acustica corespunzatoare undei incidente are directie oblica fata de suprafata de separatie a celor doua medii, aceasta se descompune intr-o componenta normala pe suprafata si o alta tangentiala care actioneaza de-a lungul planului de separatie, formandu-se in final atat unde longitudinale, cat si unde transversale. Undele transversale se vor reflecta in directia OR' si se vor transmite in cel de-al doilea mediu in directia OT'.

Directiile de propagare a undelor se pot determina aplicand legea lui Snell:

q_r q_I (3.80)

si:

c₁/sinq_tr = c₁'/sinq'_tr = c₂/sinq_tr = c'₂/sinq'_tr    (3.81)

In care c₁, c₂ respectiv c₁' si c₂' sunt vitezele undelor longitudinale si transversale.

Din relatia de mai sus rezulta, cand q_tr

q_i = arcsin c₁/c₂    (3.82)

Deci unda longitudinala este reflectata total, ea fiind dirijata de-a lungul planului de separare.

Pentru unghiuri de incidenta mai mari decat cele rezultate din valoarea data de relatia anterioara, in cel de-al doilea mediu nu mai sunt transmise unde longitudinale,existand doar cele transversale.

Cand unghiul de incidenta q_i are o astfel de valoare incat unghiul de refractie corespunzator undei transversale devine egal cu 90 , respectiv q'_tr = 90 , atunci:

q_r = arcsin c₁/c'₂    (3.83)

Deci unde transversala este reflectata total, ea fiind continuta in planul de separatie a celor doua medii; pentru aceasta valoare a lui q_i in cel de-al doilea mediu neexistand decat unde de suprafata. Cele de mai sus valabile pentru c₁< c₂'.

Cunoasterea valorilor limite a unghiului de incidenta este necesara la constructia transformatoarelor de unda, in vederea transmiterii unui anumit tip de unda in corpuri solide, in special in aplicatiile tehnologice.

3.2.4. DIFRACTIA SIN DIFUZIA UNDELOR ULTRASONICE

Undele in general prezinta proprietatea de difractie(ocolire a obstacolelor) care in cazul folosirii undelor ultrasonice, pot fi: incluziuni, pori, fisuri, deci, in general, discontinuitati.

Difractia este observabila in bune conditii daca discontinuitatea are dimensiuni suficient de mici pentru a putea fi comparata cu lungimea de unda.

Fenomenul conta in micsorarea domeniului de umbra din spatele discontinuitatii, perpendicular pe directia de propagare. Unghiul de difractie, pentru fante circulare se exprima prin relatia:

sinq l D (3.84)

Unghiul q este direct proportional cu l si invers proportional cu dimensiunea reflectorului.

Fenomenul de difractiea undelor se explica pe baza principiului lui Huygens, potrivit caruia undele se propaga in afara unei suprafete inchise continand sursa de oscilatie, sunt identice cu acelea care s-ar obtine suprimand aceasta sursa si inlocuind-o prin surse elementare separate, convenabil repartizate pe toata suprafata si a caror infasuratoare constituie un nou front de unda.

Obstacolele pot produce pe langa difractie si fenomenul de difuzie a undelor, fenomen prin care o parte din energia ultrasonica este deviata de pe directia de propagare.

Pentru a se realiza o evaluare a discontinuitatilor existente in materialul in care se propaga unda ultrasonica trebuie sa comparam amplitudinea sau presiunea undelor reflectate de suprafata unor defecte artificiale de dimensiuni cunoscute.

Presiunile produse de unda incidenta si cea reflectata sunt prezentate grafic in figura, unde d_e este distanta defect - palpator emitator, iar d_r este distanta palpator receptor - defect.

3.2.5. PROPAGAREA ULTRASUNETELOR IN GAZE

Formula vitezei sunetului este usor de obtinut daca ne imaginam cum se propaga o unde de presiune intr-o conducta infinit de lunga. Fie un piston aflat in conducta a carui suprafata a sectiunii transversale este egala cu unitatea. Cand are loc variatia unitatii de volum de aer atunci pistonul se deplaseaza in conducta in conformitate cu relatia:

dV/V = dx/dy (3.85)

Considerand ecuatia transformarii adiabatice pentru gaze:

pV^g = const.    (3.86)

Si diferentiand obtinem:

dp/p = - c (dV/V) = - c (dx/dy)    (3.87)

La deplasarea pistonului in conducta presiunea variaza dupa legea:

p = p₀ - cp₀(dx/dy)    (3.88)

Caderea de presiune, adica forta care actioneaza pe unitatea de volum a gazului va fi egala cu:

- (dp/dy) = p₀c((d²x)/(dy²))    (3.89)

Dupa legea a doua a dinamicii aceasta forta reprezinta produsul dintre masa gazului din unitatea de volum si acceleratia sa:

p₀c((d²x)/(dy²)) = r(d²x)/(dt²)    (3.90)

Ecuatia precedenta se mai poate scrie:

x) t²) = (cp₀/r x y (3.91)

Aceasta ecuatie coincide cu ecuatia:

x) t²) = c² ( x y (3.92)

De unde rezulta ca viteza undelor longitudinale in gaze egala cu:

c = (cp₀/r (3.93)

3.2.6. PROPAGAREA ULTRASUNETELOR IN LICHIDE

Expresia anterioara o putem folosi pentru determinarea vitezei sunetelui in lichide.

Daca luam in considerare ca oscilatiile se produc adiabatic, adica viteza de variatie a presiunii este atat de mare incat se poate neglija schimbul de caldura dintre straturile vecine, in acest caz viteza este definita de compresivitatea adiabatica si de densitatea mediului lichid.

Astfel:

c = (1/rK (3.94)

Unde K este compresivitatea si se poate determina din expresia:

K = 1/cp    (3.95)

Compresivitatea lichidelor este cu cateva ordine de marime mai mica decat a gazelor, de aceea independent de densitatea lor mare, comparativa cu cea a gazelor, viteza sunetului in lichide este considerabil mai mare decat in mediile gazoase.

3.2.7. PROPAGAREA ULTRASUNETELOR IN MEDII SOLIDE

Viteza de propagare a undelor longitudinale intr-o bara se defineste dupa formula:

c = (E/r (3.96)

Expresia anterioara este valabila pentru unde elastice longitudinale care se propaga in bare ale caror dimensiuni sunt cu mult mai mici decat lungimea de unda. Daca undele longitudinale elastice se propaga intr-un corp solid nelimitat, viteza lor se va determina dupa formula:

c = (E(1-m r m m (3.97)

Unde m este coeficientul lui Poisson.

Din ecuatia anterioara se vede ca viteza undelor elastice longitudinale este determinata de densitate si constantele elastice ale mediului. In Tabelul 3.2. se indica pentru unele materiale solide valorile vitezei de propagare a undelor acustice, densitati si rezistente acustice specifice.

Viteza de propagare a undelor longitudinale intr-un corp solid nelimitat este mai mare decat in bare. Aceasta diferenta se explica prin aceea ca in medii nelimitate, la propagarea undelor, fiecare element de volum sufera o compresiune sau intindere laterala, suplimentara, din partea elementelor de volum vecine.

Undele transversale elastice pot fi excitate atat intr-un volum limitat al unui corp cat si intregul corp. Luand de exemplu o bara suspendata de o sfoara si aplicand o lovitura la capatul ei, perpendicular pe suprafata laterala, in locul unde s-a aplicat lovitura, un strat de particule din corpul solid se va deplasa din pozitia de echilibru, adica va executa o miscare de alunecare. Prezenta fortelor de elasticitate, dintre particulele barei, provoaca deplasarea stratului invecinat iar in bara apare o unda de alunecare care se raspandeste in lungul barei.

Viteza de propagare a undelor transversale este definita de relatia:

c_t = (G/r (3.98)

Si este de doua ori mai mica decat a undelor longitudinale(G este modulul de elasticitate transversal.)

Expresia anterioara se mai poate scrie sub forma:

c_t = ((E/r m

Unde:

E = 2G(1+m (3.100)

Unde analoage acelor unde care se propaga pe suprafata apei pot fi produse pe o suprafata libera a unui corp solid elastic prin forte de elasticitate si inertie.

Astfel de unde se amortizeaza repede, aproape ca nu patrund in volumul corpului iar traiectoria particulelor corpului solid reprezinta aproximativ cercuri a caror suprafata coincide cu directia de propagare a undei. Traiectoriile de deplasare ale particulelor undelor de suprafata au componente paralele si perpendiculare pe suprafata corpului elastic.

Viteza acestor unde (unde Rayleigh) care se propaga pe suprafata unui solid se definesc dupa formula:

c_s = (0,87+1,22m m)(G/r 0,9(G/r (3.101)

Si nu depinde de lungimea lor de unda. Aproximativ se poate considera ca viteza undelor de suprafata este egala cu 0,9 din viteza undelor transversale   

3.3. CARACTERISTICILE FASCICULULUI ULTRASONIC

3.3.1. CAMPUL ACUSTIC AL UNUI EMITATOR CIRCULAR

Din notiuni de simetrie, repartitia energeica se face circular sau inelar. De la emitator pe axa z, campul se imparte in:

camp apropiat care se intinde pana la N = D l

camp indepartat care se intinde dupa N = D l

In campul acustic indepartat presiunea se exprima prin relatia:

P = (P₀/Z)(2J₁klsinl /kDsing

Unde P_o este presiunea ultraacustica pe axa x, Z - distanta, k =2 p/2 - numarul de unda, J₁ - functia Bessel, l - lungimea de unda, D - diametrul emitatorului, g_o - unghiul pe care il face directia de propagare cu o dreapta ce uneste traducatorul cu un punct din spatiu in care se calculeaza P.

In campul acustic apropiat, expresia care da presiunea campului ultrasonic este foarte complicata. Limita campului apropiat se obtine cu relatia D l

3.3.2. DIFRACTIA FRASNEL IN CAMP APROPIAT

Se considera ca emitatorul are un numar infinit de puncte ce devin microsurse de la care pleaca undele Huygens. Acestea interfera si dau un front de unde plane care se propaga pe o directie perpendiculara fata de suprafata cristalului. In interiorul cristalului are loc o anulare reciproca a undelor produse de microsursele invecinate.

La suprafata cristalului undele emise nu se anuleaza complet, pentru ca nu exista compensatie vecina exterioara pentru undele Huygens. Astfel, se genereaza un camp ultrasonic cu o variatie de intensitate.

La distanta D l de cristalul piezoelectric,ultimul maxim al intensitatii ultrasonice imparte campul ultraacustic in doua zone (fig 3.3):

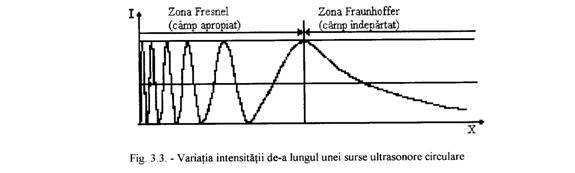
zona Fresnel, situata intre emitator si ultimul maixim, numita camp apropiat;

zona Fraunhofer, situata dupa ultimul maxim, numit camp indepartat.

In cazul zonei Fresnel(campul apropiat), pozitia maximelor si minimelor se calculeaza cu relatiile:

A_Max = D - (2ml)²/8ml ; m = 1,2,3,.    (3.102)

A_Min = D - (2(n/2)l)²/8(n/2)l , n = 1,2,3,. (3.103)

In zona Fraunhoffer, la o distanta mai mare de pozitia ultimului maxim al intensitatii ultrasonice, suprafetele de unda sunt sferice, avand centrul comun cu cel al sursei circulare. In aceasta zona intensitatea acustica scade continuu, invers proportional cu patratul distantei:

I = P/4pd² (3.104)

3.3.3. LEGEA MARIMII DEFECTULUI

In campul indepartat al unui palpator, inaltimea ecoului ultrasonic provenit de la o discontinuitate depinde de puterea impulsului, amplificarea la care este reglat aparatul, de diametrul D al palpatorului , de lungimea de unda l a ultrasunetelor, de diametrul defectului D, si de distanta d intre palpator si defect(fig.3.4)

Se disting patru zone:

zona I, unde D/l<<1/2, adica defectul presupus in forma de disc perpendicular pe fasciculul ultrasonic are un diametru mai mic decat l, nu apare ecou si el nu va putea fi detectat. In acest se recomanda utilizarea unor frecvente ridicate.

zona II, unde inaltimea de ecou ultrasonic creste cu aproximativ (D/l)², adica proportional cu suprafata defectului.

zona III, inaltimea de ecou ultrasonic creste proportional cu D/l, adica proportional cu diametrul defectului.

Limita intre regiunile III si IV depinde de distanta d de la palpator la defect si de diametrul D al palpatorului. Pana la acest punct se presupune ca defectul se afla in intregime in interiorul fasciculului ultrasonic. In zona IV inaltimea ecoului creste mai incet si se aproximeaza inaltimea maxima a ecoului atunci cand suprafata defectului este mult mai mare decat sectiunea fasciculului ultrasonic.

3.4. PRODUCEREA ULTRASUNETELOR

3.4.1. INTRODUCERE

Orice sistem mecanic capabil sa vibreze cu o frecventa cuprinsa in domeniul ultrasunetelor constituie o sursa de ultrasunete.

In general trebuie facuta o distinctie in cadrul generatoarelor de ultrasunete intre sistemele care genereaza energie si cele care primesc aceasta energie si o transfera altui sistem (mediu de propagare) sub forma frecventa inalte de vibratie mecanica. Aceste sisteme apartin categoriei traductoarelor.

Energia generata de traductoare poate fi electrica sau mecanica. Traductoarele ultrasonice pot fi impartite in doua grupuri in functie de energie folosita: electrica sau mecanica. Primului grup apartin urmatoarele traductoare, enumerate in ordinea in care ele sunt folosite: traductoare piezoelectrice, traductoare magnetostrictive, traductoare electrodinamice, traductoare electrostatice, traductoare prin scanteie. Al doilea grup include acele traductoare in care presiunea sau viteza fluidului primind energie este modulat la frecventa inalta cu ajutorul unui element mecanic fixat sau cu ajutorul unui element mecanic mobil.

Materialele utilizate ca traductori trebuie sa indeplineasca mai multe conditii ca:

a)      sa prezinte caracteristici piezoelectrice satisfacatoare pentru modurile de vibratie necesare;

b)      sa poata fi prelucrate in forma si marimea dorita;

c)      proprietatile lor sa aiba variatii mici cu temperatura;

d)      sa aiba frecari interne cat mai mici;

e)      sa fie stabile fizic si chimic;

f)        sa-si pastreze proprietatile piezoelectrice in intregul domeniu de temperaturi in care vor fi utilizate.   

In plus, pentru eficienta maxima, traductorul trebuie sa se potriveasca atat cu circuitul electric cat si cu mediul de propagare si sa nu dea nastere la vibratii parazite care pot apare atat din cuplarea diferitelor moduri de vibrare cat si din armonici apropiate de modul de vibratie fundamentala.

3.4.2. TRADUCTOARE PEZOELECTRICE

Aceasta traductoare sunt bazate pe efectul piezoelectric.

Unele materiale cristaline se polarizeaza atunci cand sunt supuse unor tensiuni mecanice. Prin inversarea directiei fortei de tensiune mecanica aplicata asupra materialului polarizarea isi schimba sensul. Pe de alta parte, daca materialul este supus actiunii unui camp electric prin aplicarea unei diferente de potential intre 2 fete opuse ale lui, materialul se deformeaza si forta de deformare isi schimba sensul cand sensul campului electric este inversat.

O placuta dintr-un material piezoelectric poate fi astfel determinat sa genereze unde elastice. Intr-adevar, daca diferenta de potential aplicata este alternativa, elementul vibreaza si vibratiile sale mecanice sunt transferate mediului inconjurator.

Cele mai importante materiale piezoelectrice aplicate in acustica sunt: cuartul (SiO₂), turmalina (cristalizata in sistem trigonal), sulfatul de litiu (Li₂SO₄+H₂O), fosfatul de amoniu dehidrogenat (NH₄H₂PO₄) (tetragonal), sarea Rochelle (NaKC₄H₄O₆+4H₂O) (rombic) si titanatul de bariu polarizat (BaTiO₃) (tetragonal).

Cuartul si titanatul de bariu sunt cele main utilizate datorita stabilitatii proprietatilor lor mecanice, chiar si atunci cand vibratia are o amplitudine considerabila. Traductorul de cuart consta dintr-o placuta taiata dintr-un cristal natural. Traductorul din titanat de bariu este o ceramica in care proprietatile piezoelectrice sunt artificial induse.

a)      Traductorul din cuart.

Cuartul cristalizeaza in sistem trigonal formand o prisma hexagonala cu 2 capete romboedrice ca in fig.3.5. Cele trei axe care unesc varful sectiunii transversale ale prismei se numesc axe piezoelectrice(x₁,x₂,x₃). Axele prismei ce trece prin centrul sectiunii se numesc axe mecanice(y₁,y₂,y₃). Axa prismei ce trece prin centrul sectiunii este axa de simetrie optica, numita si axa optica a cristalului. In lungul acestei axe lumina nu sufera fenomenul dublei refractii, dar se observa fenomenul de polarizare rotatorie a luminii.

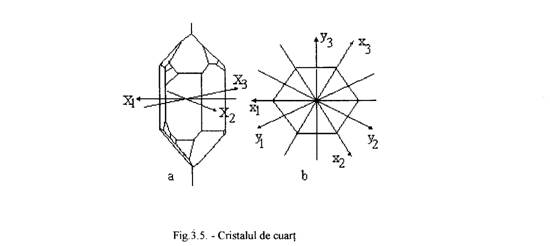
Pentru generarea undelor longitudinale placuta traductorului este taiata din cristal pe o directie perpendiculara pe una din axele piezoelectrice. Placuta astfel obtinuta este de forma dreptunghiulara sau circularasi se numeste cu taietuta x.

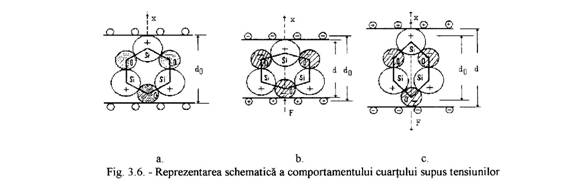
O schema simpla a unei retele cristaline nedeformate este aratata in fig.3.6.a. Se observa ca sarcinile ionice pozitive de siliciu si cele negative de oxigen se neutralizeaza astfel incat pe fetele placutei nu apare o concentrare de sarcini de un anumit tip.

Cand se aplica o forta de tensiune pe aceste suprafete in directia lui x (fig.3.6.b.) atunci ionii de siliciu sunt impinsi spre fata superioara iar ionii negativi de oxigen spre fata inferioara, corespunzator deformarii [(d-d_o)/ d_o] cauzate. Echilibrul sarcinilor electrice de pe suprafetele placutei este perturbat si aceasta conduce la o diferenta de potential V intre cele doua fete. Daca directia fortei de tensiune mecanica aplicata se inverseaza (fig.3.6.c), sensul de deformare este de asemenea inversat si, din motive similare celor expuse mai sus, distributia de sarcina de pe fetele placutelor isi va schimba semnul si diferenta de potential devine -V. Aceasta se numeste efectul piezoelectric longitudinal.

Din aplicarea unei tensiuni mecanice perpendiculare pe axa x (in directia lui y), cum este aratat in fig.3.6.c. este obtinuta o distributie de sarcina ce are ca rezultat efectul piezoelectric transversal . Invers,daca elementul este supus unui camp electric in directia lui x prin aplicarea unei diferente de potential intre fetele placutei, sarcinile ionice sunt determinate sa se miste in directia campului aplicat, dand nastere unei forte de comprimare proportionala cu grosimea placutei (efectul piezoelectric invers).

Aceste comprimari produc efecte mecanice si electrice in diferite directii ale elementului. O descriere generala a fenomenului este data de ecuatiile care stabilesc relatii corespunzatoare intre constantele piezoelectrice, elastice si dielectrice ale cuartului.

Urmand notatiile lui Voigt putem reprezenta in fiecare caz prin cateva ecuatii tensoriale comportarea unui cristal de forma paralelipipedica,taiat in directia axelor cristalului asa cum este indicat in figura 3.7.

Daca S_k este tensorul tensiunii electrice, avand componentele longitudinale: x_x, y_y, z_z iar cele transversale x_y, y_z, z_x obtinem:

S_k = åd_ikE_i    (3.106)

ⁱ

Unde d_ik reprezinta constanta de tensiune piezoelectrica (cu I=1,2,3 si h,k=1,6); E_i reprezinta cele trei componente ale vectorului camp electric. Asta inseamna ca fiecare compoonenta a campului electric contribuie la producerea tensiunii longitudinale si tangentiale de-a lungul axelor x,y,z.

In cazul unei taieturi in lungul axei x a placutei de cuart, asa cum este aratat in figura, multi coeficienti sunt zero iar altii sunt simplificati datorita simetriei. Astfel sistemul de 6 ecuatii reprezentat de relatia (3.106) este redus la urmatoarele relatii simple:

x_x = d₁₁E_x,

y _y = - d₁₁E_x ,

y_z = d₁₄E_x ,    (3.107)

z_x = - d₁₄E_y,

x_y = - 2d₁₁E_y,

Unde constantele d₁₁ si d₁₄ au urmatoarele valori numerice:

d₁₁ = 2,3 10^-12 Coul/Nt    (3.108)

d₁₄ = 5,66 10^-12 Coul/Nt

Tensiunile piezoelectrice sunt conform relatiei (1), legate de deformarile elastice prin ecuatiile tensoriale date de forma generala a legii lui Hooke:

T_k = åc_kkS_k,    (3.109)

^k

Unde T_k este tensorul deformarii elastice si are trei componente normale: X_x, Y_y, Z_z si trei componente tangentiale: X_y, Y_z, Z_x, iar c_kk reprezinta constantele elastice de rigiditate, care sunt in numar de 36.

Introducand o relatie noua intre constantele de tensiune piezoelectrica e_ik si constantele de deformare d_ik obtinem:

e_ik = åc_kkd_ik,    (3.110)

^k

Si astfel poate fi stabilita o relatie intre componentele tensiunii mecanice T_k si cele ale campului electric E_i. Din constructia placutei de cuart numarul constantelor independente e_ik este considerabil redus si sistemul de ecuatii ce rezulta din relatiile (3.109) si (3.110),prin eliminarea coeficientilor c_kk devine:

X_x = e₁₁E_x,

Y_y = - e₁₁E_x,

Y_z = e₁₄E_x,    (3.111)

Z_x = - e₁₄E_y,

X_y = - e₁₁E_y,

Traductorul este evident excitat pe unul din modurile sale mecanice. Din cauza faptului ca placuta vibreaza in directia grosimii ei, frecventa naturala a oscilatiilor elastice este aceea care determina maximul elongatiei celor 2 fete in doua directii opuse, situatie descrisa de undele elastice stationare cu deplasarea antinozilor pe ambele fete.

In cazul primului mod normal de vibratie este un singur plan nodal si grosimea lui d este egala cu ½ din lungimea de unda. In acest caz frecventa de oscilatie devine:

= c/l = 1/2d(c₁₁/r

Unde c₁₁ este modulul elastic in directia lui x si r este densitatea cuartului.

In practica valoarea masurata a lui f difera putin fata de cea calculata corespunzator marimii placutei de cuart.

In conditii standard alte oscilatii decat cele in directia lui x, interactioneaza cu oscilatiile in directia grosimii placii, modificandu-I frecventa naturala.

b)      Titanatul de bariu.

Asa numitul efect piezoelectric al titanatului de bariu poate fi tratat prin fenomenul general de electrostrictiune - o proprietate corespunzatoare materialelor dielectrice - si consta in proportionalitatea deformarii cu patratul campului electric aplicat.

Acest efect este nesemnificativ in materiale dielectrice obisnuite dar atinge valori apreciabile in ceramicile de titanat de bariu. Aceste ceramici sunt obtinute prin amestecarea titanatului de bariu in forma cristalina cu alte saruri ce poseda proprietati electrostrictive si se incalzeste amestecul la o temperatura in jur de 1300 - 1400 C. Acestea conduc la obtinerea unui material caruia daca i se aplica un camp electric de 10⁶V/m produce o tensiune de 3x10^-4V.

Elementele de orice configuratie: placi, sfere, cilindrii etc. pot fi polarizate cu succes. Pentru folosirea ceramicilor ca traductoare, acestea trebuie sa fie polarizate corespunzator. Daca este adaugata o componenta alternativa campului de polarizare, se obtine o deformare mecanica periodica care variaza liniar, in limitele stabilite,cu tensiunea electrica aplicata. Componentele continue si alternative ale campului sunt orientate in directia grosimii materialului. Pe de alta parte, daca este aplicata o forta elementului polarizat in directia orientarii campului atunci se va observa o variatie a campului electric direct proportionala cu tensiunea mecanica observata in material.

Aceste proprietati dau nastere unor efecte similare cu cele observate in materialul piezoelectric. Pentru aceste motive traductoarele de titanat de bariu sunt privite ca niste traductoare piezoelectrice.

Una din caracteristicile fundamentale ale acestor ceramici este faptul ca apare o polarizare permanenta daca aplicam un camp de curent continuu in jurul a 2000 V/cm,in lungul grosimii elementului, la o temperatura apropiata de punctul de tranzitie (120 C) si este mentinut in timpul unei raciri treptate. In acest mod nu mai este nevoie sa adaugam un camp electric direct tensiunii alternative.

Atat timp cat polarizarea reziduala depinde de tendinta domeniilor de dipoli de a ramane aliniati in directia campului indus, este necesar sa ne asiguram ca efectul termic si campul alternativ nu vor modifica apreciabil aceasta tendinta. Adaugarea de titanat serveste in acest scop prin ridicarea punctului de tranzitie.

Acest fapt impune limitarea valorilor tensiunii alternative si temperaturii. Pe de alta parte, proprietatile piezoelectrice ale titanatului de bariu sunt superioare acelora ale cuartului.

Suprafetele traductorului intre care este aplicata o tensiune electrica sunt in general acoperite cu un strat subtire de argint. Modurile de vibratie ale traductorului depind de forma, directia si prepolarizarea campului si de configuratia fetelor pe care se aplica tensiunea.

In figura sunt prezentate unele tipuri de traductoare de titanat de bariu. Frecventele obtinute cu traductoarele de titanat de bariu sunt mai joase decat ale celor de cuart, in primul rand din cauza pierderilor datorate hesterezisului dielectric si dificultatii de a obtine traductoare foarte mici. Traductoarele sub forma de placute sunt in general folosite pentru obtinerea frecventei de la cateva sute de kHz la cativa MHz.

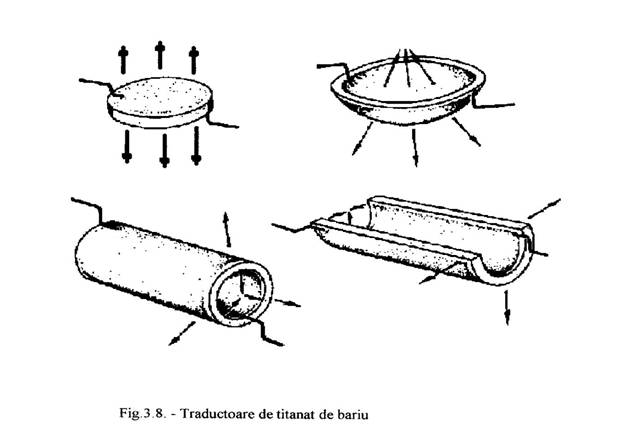
Traductoarele de titanat de bariu au o impedanta mai mica decat cele de cuart, astfel incat pentru obtinerea unei aceleiasi puteri de radiatie acustica este necesara aplicarea unei tensiuni electrice mai ridicate.

3.4.3. TRADUCTOARE MAGNETOSTRICTIVE

Daca un material feromagnetic este supus actiunii unui camp magnetic, in material apare o forta de tensiune mecanica. Invers, daca acelasi material este deformat ca rezultat al aplicarii unor forte exterioare, este observata o variatie a proprietatilor sale magnetice. In concordanta cu metodele experimentale s-au investigat variatiile diferitelor aspecte ale acestor fenomene ca: variatia in lungime observate intr-o bara cand este aplicat un camp magnetic coaxial asupra ei(efectul Joule). Efectul invers arata influenta unor forte mecanice ce actioneaza asupra materialului (efectul Villari).

Principalele materiale ce preinta efectul magnetostrictiv sunt: nichelul, cobaltul si aliajele lor in diferite combinatii. Astfel de aliaje contin de multe ori cantitati din alte metale: cupru, crom, vanadiu etc.

Intr-o bara alungirea datorata magnetostrictiunii depinde de tipul metalului si nu depinde liniar de variatia intensitatii campului magnetic.

Dupa cum este aratat in figura, in cazul nichelului,apare o scurtare a barei la orice valoare a intensitatii campului. Pe de alta parte o bara de fier se alungeste in prezenta unui camp slab si se scurteaza in prezenta unui camp mai puternic.

Efectul magnetostrictiv depinde de temperatura si devine zero in punctul Curie, unde proprietatile magnetice ale materialului dispar.

Figura arata tensiunea interna ca apare intr-o bara de nichel atunci cand este crescuta temperatura. Curbele au fost desenate pentru cateva intensitati relative ale campului magnetic.

O relatie simpla leaga alungirea relativa a materialului si inductia B din material. Aceasta relatie se pastreaza bine pentru valori mici incepand de la o inductie B_o data:

DL/L = KB₀DB    (3.113)

Coeficientul K nu este constant, el depinde de B_o . De exemplu, in cazul nichelului K=-2x10³ daca B_o= 0,5Wb/,m².

In constructia traductoarelor magnetostrictive valoarea lui B_o va fi aleasa in asa fel incat, pentru valori egale ale lui DB valoarea tensiunii mecanice devine maxima. In forma simpla, un traductor consta intr-o tija din material magnetostrictiv introdus intr-un solenoid traversat de un curent electric ce are o componenta continua necesara producerii inductiei magnetice B_o si o componenta alternativa capabila sa produca vibratii in tija astfel incat oscilatiile sa atinga o amplitudine considerabila.

Polarizarea tijei datorita componentei continue este importanta pentru a impiedica tija sa oscileze la o frecventa de doua ori mai mare decat aceea de excitare.

Intr-o substanta data efectul magnetostrictiv apare intotdeauna in aceeasi directie, chiar daca polarizarea campului magnetic isi schimba semnul. In timpul fiecarei perioade de oscilatie de excitatie de bara se contracta si dilata de doua ori in aceeasi maniera.

Nichelul pur, asa cum am vazut, are cele mai bune proprietati magnetostrictive, motiv pentru care este frecvent folosit. Punctul sau Curie este la 360 C iar rezistenta scazuta la oboseala il face sa fie mai putin recomandat pentru producerea unor puteri acustice mari.

Fierul pur prezinta un efect magnetostrictiv mai slab decat nichelul iar la o anumita valoare a campului magnetic magnetostrictiunea isi schimba semnul. De exemplu adaugarea unei cantitati mici de nichel este suficienta pentru a produce magnetostrictiunea pozitiva pentru toate valorile campului magnetic care poate fi aplicat. Aliajele de fier si cobalt comporta un efect magnetostrictiv pronuntat. Unul dintre aceste aliaje (permendur) este folosit frecvent si consta din parti egale de cobalt si fier plus 2% vanadiu care are rolul de a creste proprietatile magnetostrictive.

Partile esentiale ale generatorului magnetostrictiv sunt ilustrate in figura. Elementul magnetostrictiv (de exemplu nichelul) sub forma unei tije sau tevi este fixat in centrul unei linii nodale cu un suport rigid capabil sa-I permita oscilatia libera in modul sau fundamental de vibratie extensionala. Elementul magnetistrictiv este plasat in interiorul solenoidului L al circuitului rezonant al tijei.

Polarizarea elementului magnetostrictiv poate fi obtinuta in mai multe feluri:

a)      folosind o componenta continua a curentului anodic a tubului de vid;

b)      folosind o putere separata suplimentara, trimisa prin intermediul unei frecvente inalte, pentru obtinerea curentului necesar solenoidului L;

c)      cu ajutorul unui solenoid separat, coaxial cu L (vezi fig.3.9.);

d)      prin plasarea unui magnet permanent sau a unui magnet permanent sau a unui electromagnet in apropierea barei astfel incat fluxul magnetic rezultat de la expasiunea polara sa penetreze tija in lungul ei.

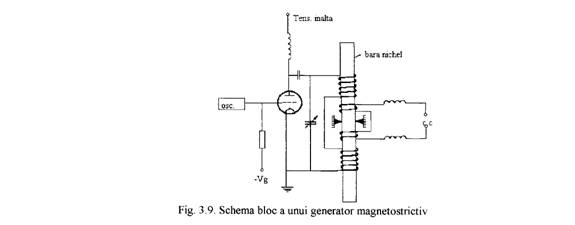
In unele generatoare ce au o constructie simpla tubul de iesire care transmite oscilatiile traductorului este autoexcitat prin intermediul unui feedback corespunzator si actioneaza ca un oscilator simplu a carui frecventa este examinata de vibratia elementului magnetostrictiv.

In reglarea generatorului trebuie acordata atentie faptului ca inductia magnetica modifica(uneori foarte putin) valoarea modulului lui Young E al elementului magnetostrictiv. Acest lucru conduce la o variatie a vitezei sunetului in metal si, ca urmare, a freventei sale de vibratie mecanica.

Frecventa maxima ce poate fi obtinuta este limitata de pierderile electrice datorate histerezisului si curentilor turbionari. Aceste pierderi sunt legate de permeabilitatea magnetica si de rezistivitate. Un sistem des folosit pentru limitarea curentilor turbionari consta in efectuarea unor taieturi in lungul barei prin care circuitul lor electric este intrerupt. Mult mai eficienta este laminarea miezului tijei in aceeasi maniera ca la transformatoare.

3.4.4. CONSTRUCTIA SI FUNCTIONAREA PALPATOARELOR

Prin palpator se intelege ansamblul format din traductorul piezoelectric cu montura sa, completat de partea electrica de conectare la aparat. Acesta trebuie realizat astfel incat zgomotul intern sa nu perturbe interpretarea indicatiilor obtinute pe ecran, la sensibilitatea de lucru aleasa. Traductorul este confectionat dintr-un material piezoelectric si reprezinta dispozitivul care transforma energia electrica in energie mecanica si invers. Dintre toate materialele piezoelectrice, in defectoscopie cel mai des utilizate sunt cuartul si materialele ceramice sintetizate. Cuartul prezinta o serie de avantaje cum ar fi: buna stabilitate chimica, electrica si termica; insolubilitate in cele mai multe lichide; tarie si rezistenta la uzura si imbatranire. De asemenea, cuartul prezinta si un mare dezavantaj prin faptul ca, dintre toate materialele piezoelectrice, acesta genereaza o energie acustica slaba, fiind nevoie de o tensiune inalta, mai mare decat cea necesara materialelor ceramice sintetizate. Aceste materiale sunt bune materiale generatoare de energie, dar fragile la temperaturi joase si solubile in apa.

Traductorul, indiferent de materialul din care este confectionat este montat intr-un ansamblu care permite aplicarea tensiunilor electrice, protectia cristalului, precum si posibilitatea de a-l prea pe suprafata piesei examinate. Ansamblul respectiv este format din traductor, pe suprafata caruia se aplica electrozi, corpuri de amortizare si sistem electric de adaptare, toate acestea montandu-se intr-o carcasa metalica pentru a se obtine o soliditate mecanica.

Daca traductorul este paralel cu suprafata piesei, undele emise sau receptionate sunt transversale iar palpatorul se numeste normal sau drept.

Dand traductorului o inclinare fata de suprafata piesei de examinat undele emise sau receptionate sunt transversale iar palpatorul se numeste unghiular sau inclinat.

In cazul uni palpator de unde longitudinale, fascicolul ultrasonic va avea doua zone distincte: zona campului apropiat si zona campului indepartat. In zona campului apropiat intensitatea fasciculului variaza neregulat in timp,deci inaltimea ecourilor variaza de o maniera complexa si nu se pot interpreta. In zona campului indepartat intensitatea descreste continuu cu distanta, ecourilor de defect fiind proportionale cu aceasta. Ca urmare atunci cand se face alegerea palpatoarelor pentru lucru, trebuie cunoscuta mai intai lungimea campului apropiat, dependent de frecventa si diametrul traductorului, pentru a putea fi evitata aceasta zona. De asemenea, trebuie determinate caracteristici cum ar fi rezolutia si sensibilitatea. Sensibilitatea se defineste ca fiind capacitatea unui palpator de a depista discontinuitati mici, deci de a transmite spre partea de receptie a aparatului un impuls mare de la un defect mic. Rezolutia se defineste ca fiind capacitatea unui palpator de a separa undele reflectate de doua discontinuitati aflate la o diferenta de adancime cat mai mica. Aceste caracteristici ale palpatorului depind de frecventa de lucru a cristalului si de marimea acestuia. Palpatoarele normale au frecventa de lucru cuprinsa intre 0,5 si 15 MHz, iar cele inclinate intre 1 si 5 MHz, de obicei 2 MHz si 4MHz. Corect spus, traductoarele lucreaza intr-o banda de frecvente. De exemplu, un palpator despre care se spune ca are frecventa de lucru de 4MHz va lucra in banda de frecvente (3 5)Mhz.

Frecventa unui palpator este dependenta si de marimea acestuia, de fapt marimea acestuia este limitata de frecventa joasa. Se stie faptul ca un cristal mare si subtire este mai fragil decat unul de dimensiuni mai mici. Daca avem de a face cu suprafete rugoase este necesara o mare putere de penetrare, se transmite de la piesa cu pierderi mari din cauza faptului ca traductorul, avand dimensiuni mari, este fragil si pericolul de spargere este mare. Ca urmare a acestui fapt, pentru a se obtine palpatoare cu dimensiuni mai mari se foloseste un mozaic de cristale, avand insa dezavantajul ca intensitatea fascicolului este foarte mica.

Palpatoarele normale ca marime au diametre de 24mm sau de 34mm pentru frecvente sub 1 MHz. De asemenea, exista palpatoare cu diametrul de 10 mm, numite miniaturale si cu diametre de 5 mm sau chiar mai mici, numite subminiaturale.

Palpatoarele pot fi prevazute cu folie de protectie, aceasta nefiind insa o cerinta obligatorie. De asemenea, exista palpatoare speciale, utilizate in cadrul metodei de examinare in imersie, si traductoare cu talpa adaptata curburii in cazul examinarii unor suprafete curbe.

In cazul palpatoarelor curbe inclinate, unghiurile de refractie in otel sunt de 35 si 90 , caz in care avem de a face cu unde de suprafata. De asemenea se construiesc si palpatoare cu unghi variabil, in acest caz palpatorul fiind umplut cu cuplant.

De o deosebita utilitate tehnica se bucura palpatoarele emisie-receptie cu dublu cristal. Cele doua unitati, de emisie si de receptie sunt similare din punct de vedere constructiv, fiecare continand cate un traductor realizat din titanat de bariu care se cupleaza cu materialul investigat prin intermediul unor blocuri de plexiglas si a cuplantului folosit. Cele doua unitati ale palpatorului sunt izolate intre ele din punct de vedere acustic prin intermediul unui strat subtire de pluta. Un asemenea tip de palpator are cea mai buna rezolutie, deoarece zona moarta este redusa intre transmisie si receptie si nu are loc fenomenul de interferenta acustica. Palpatorul emisie-receptie cu dublu cistal este folosit intr-o serie de aplicatii, cum ar fi: investigarea materialelor cu granulatie mare, ce produc o imprastiere considerabila a fasciculului ultrasonic,aici folosindu-se palpatori dublu cristal inclinati sub unghiuri convenabile; masuratori de grosimi; investigarea materialelor continand un numar mare de incluziuni.

3.4.5. CONSTRUCTIA SI FUNCTIONAREA DEFECTOSCOAPELOR

La baza unui echipament de examinare ultrasonic stau o serie de elemente comune: aparatul generator-indicator, palpatoarele, cablurile de legatura, adaptoarele, blocurile de calibrare, reglare si accesoriile specifice aparatului.

Aparatul generator-indicator produce trenuri de unda foarte scurte de cate 2, 3 oscilatii puternic amortizate. Oscilatiile sunt generate si receptionate de un singur palpator (tehnica reflexiei), sau generate de unul si receptionate de altul(tehnica transmisiei).

Metoda reflexiei presupune generarea de impulsuri scurte, introducerea lor in piesa de examinat prin intermediul palpatorului si urmarirea timpului de propagare al undelor si amplitudinii impulsurilor reflectate de orice suprafata separatoare de mediu. Impulsurile ultrasonice generate si reflectate sunt prezentate pe ecranul tubului catodic la o distanta pe axa orizontala proportionala cu distanta parcursa de unda pana la discontinuitatea de care se reflecta.

Schema bloc a unui defectoscop ultrasonic cuprinde:

- tubul catodic;

- blocul de inalta tensiune;

- blocul de baleiaj;

- blocul emitator;

- amplificator;

- monitor;

- palpator

Impulsul de inalta frecventa este ransformat de palpator intr-un tren de oscilatii mecanice. La receptie, sub actiunea undelor mecanice, cristalul piezoelectric produce un tren de oscilatii mecanice care se aplica blocului amplificator. Acesta ridica semnalul atenuator calibrat care serveste la aprecierea marimii defectului. Amplificatorul este de banda larga si zgomot mic. Emitatorul genereaza impulsuri de inalta frecventa pentru excitarea traductorului simultan cu amorsarea cursei de baleiaj pe orizontala. Timpul de emisie are o durata scurta comparativ cu durata dintre doua impulsuri pentru a se putea desfasura semnale din piesa. De asemenea, acest bloc comanda momentul generarii impulsului de emisie, viteza sa fiind reglata de sincronizator. Monitorul serveste la avertizarea automata (acustica sau optica) asupra aparitiei unor semnale de discontinuitate care depasesc un anumit nivel din inaltimea ecranului si la inregistrarea semnalelor de defect.

Pentru realizarea sincronizarii emisiei impulsurilor si receptiei semnalelor reflectate, aparatul dispune de un generator sincronizator care comanda baleiajul intre placile orizontale ale tubului catodic, formand baza de timp necesara masuratorilor. Afisarea pe ecran se realizeaza propotional cu distanta parcursa de fasciscul in urmatoarea succesiune: impulsul de emisie, impulsul reflectat de la defect, impulsul reflectat de suprafata opusa.

Baza de timp apare pe ecranul aparatului la scurt timp de la comutarea butonului de pornire, ca o linie luminoasa orizontala, si marcheaza timpul in care ultrasunetul parcurge piesa, de la suprafata de intrare la suprafata opusa acesteia si inapoi. La unele aparate exista posibilitatea reglarii focalizarii, latimii acestei linii, in acest caz fiind necesar ca acesta sa fie cat mai stralucitoare. Pe ecranul aparatului, partea din stanga se considera ca punct de intrare a ultrasunetului in piesa, ca urmare examinarea acestuia se face de la stanga la dreapta.

3.4.6. MEDIUL DE CUPLARE SI ROLUL SAU IN DEFECTOSCOPIE

Datorita rugozitatii suprafetelor materialelor care se examineaza, intre palpator si piesa apare un strat de aer care joaca rolul unui ecran ultraacustic. Acest lucru este urmarea faptului ca palpatorul nu realizeaza un contact 100% cu suprafata investigata pe de o parte, iar in aer undele longitudinale se atenueaza foarte repede si undele transversale nu se propaga. Pe de alta parte, stiindu-se ca ultrasunetele se propaga foarte bine in solide si lichide, acest neajuns poate fi eliminat prin introducerea unui strat de cuplant intre palpator si suprafata examinata. Mediul de cuplare se poate prezenta sub forma lichida, semilichida, sub forma de pasta sau chiar solida, in cazul cleiurilor de oase sau de piele.

Cel mai bun cuplant este mercurul, dar are marele dezavantaj al unei toxicitati ridicate, si, in plus, este foarte scump.

Un cuplant bun trebuie sa aiba urmatoarele caracteristici:

a)      sa adere bine la suprafata de examinare pentru a elimina aerul;

b)      sa fie omogen, fara particule solide sau bule de aer;

c)      sa nu intre in reactie chimica cu materialul examinat;

d)      continutul de halogeni si sulf sa nu depaseasca cerintele proiectantului.

Atunci cand se alege mediul de cuplare trebuie sa fie luate in considerare urmatoarele: pozitia suprafetei de examinat, rugozitatea suprafetei, compozitia materialului investigat, temperatura materialului.

Inainte de aplicarea mediului de cuplare este recomandata utilizarea aceluiasi cuplant, atat pentru operatiile de calibrare pe blocurile de referinta, cat si pentru cele de examinare.

3.5. BLOCURI DE CALIBRARE SI CALIBRAREA PALPATOARELOR

3.5.1. BLOCUL DE CALIBRARE A1

Blocul A1 este confectionat din otel carbon armat, elaborat in cuptoare Siemens-Martin sau electrice, si trebuie sa aiba o granulatie uniforma, cu marimea grauntelui 8. Forma si dimensiunile sale sunt prezentate in figura. Din punct de vedere acustic blocul de calibrare nu trebuie sa prezinte variatii locale mai mari de 1 dB, iar viteza de propagare a ultrasunetului sa fie de 5920 20m/s. Brunarea ori durificarea suprafetelor este interzisa. Calibrarile si verificarile pe blocul A1 raman valabile numai pentru examinarea unei piese din otel nealiat, unde viteza ultrasonica este egala cu cea din bloc. La oteluri inalt aliate, viteza ultrasunetului este mai mica decat cea a blocului A1, ceea ce impune calibrari pe un bloc corespunzator. Astfel, la un otel ci 13% Cr, a rezultat, la un palpator de 70 , abateri ale unghiului de refractie de 10 , fapt ce conduce la erori mari in determinarea pozitiei defectelor.

Blocul de calibrare A1 are inglobata o piesa cilindrica din plexiglas, cu diametrul de 50mm si grosimea de 23mm, care corespunde cu timpul de propagare total (dus-intors) a undelor longitudinale prin 50mm otel. Una din suprafetele cilindrului din plexiglas este acoperita cu un strat conducator de argint, ce serveste la calibrarea cu palpatoare prin contact direct al cristalului de emisie-receptie cu suprafata de examinare. Pe langa orificiul cu diametrul de 50mm, blocul mai este prevazut cu un orificiu cu diametrul 1,5mm si cu doua fante, de unde se obtin ecouri la plasarea palpatoarelor pe suprafetele plane ale blocului. Prin electrogravura ori prin atac chimic, mai sunt marcate pozitiile relative, corespunzatoare unghiurilor de refractie ale palpatoarelor inclinate si o scara gradata de unitati de lungime. Pe latura de 200 mm a blocului de calibrare sunt marcate pozitiile relative corespunzatoare unghiurilor de refractie ale palpatoarelor inclinate si o scara gradata in unitati de lungime. Pe latura de 200 mm a blocului de calibrare, sunt marcate pozitiile relative corespunzatoare palpatoarelor cu unghiuri de refractie de 35 . Pe fata opusa acestei laturi, este marcata o scara gradata cu diviziuni din 5 in 5 mm. Latura blocului cu lungimea de 300mm este prevazuta cu marcaje pentru pozitiile relative corespunzatoare unghiurilor de refractie de 60 si 76 . Pe fata opusa acestei laturi, este gradata zona din jurul pozitiei centrului sectorului circular cu raza de 100mm, prin diviziuni milimetrice in domeniul 10mm.

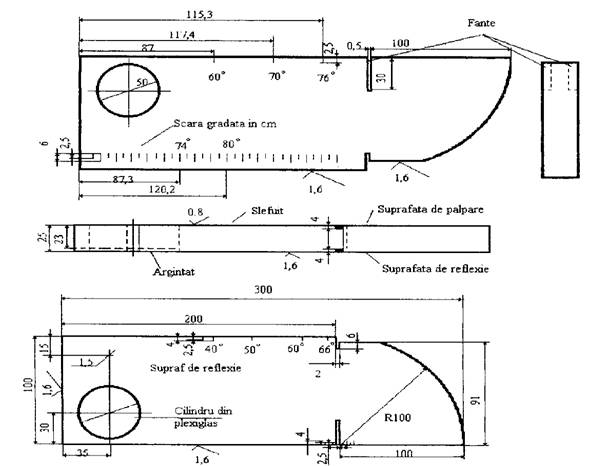
Cu acest tip de bloc se executa urmatoarele operatiuni:

a)      calibrarea scarii distantelor;

b)      corectia de zero;

c)      verificarea liniaritatii scarii de masurare a distantelor (baza de timp) si a amplificarii;

d)      calibrarea scarii distantelor, in distante proiectate si distante proiectate reduse;

e)      verificarea si reproducerea sensibilitatii aparaturii si sensibilitatii de vdetectare;

f)        verificarea zonei moarte;

g)      verificarea puterii separatoare in adancime;

h)      verificarea si determinarea punctului de incidenta al palpatoarelor inclinate;

i)        trasarea caracteristicilor de directivitate in plan orizontal si vertical pentru palpatoare inclinate;

j)        verificarea unor diferente structurale intre materialul din care este confectionat blocul A1 si alte sortimente din otel.

3.5.2. CALIBRAREA PALPATOARELOR CU AJUTORUL BLOCULUI DE CALIBRARE A1

In general calibrarea cu ajutorul blocului A1 se foloseste la palpatoare cu unde longitudinale.

Alegerea si reglarea cat mai precisa a scarii distantelor (numita si scara de profunzime) se face pentru domeniul de lucru corespunzator parcursului ultrasunetelui in piesa. In acest scop pe blocul de calibrare A1 se alege un domeniu cu o grosime de material care este foarte aproape de cea care trebuie sa fie verificata, sau un multiplu al acesteia.

De remarcat este faptul ca la o reglare corecta, ecoul initial de emisie (situat pe partea stanga a ecranului) nu se gaseste pe zero la scala aparatului, deoarece intre cristalul piezoelectric si piesa, exista cuplantul si eventual o folie din plastic pentru protectie.

Pentru grosimi de peste 50mm este recomandat a se alege cel putin doua ecouri de fund, de exemplu pentru grosimea de 80mm se fixeaza palpatorul pe blocul de calibrare A1 unde grosimea este de 100mm si se alege domeniul de lucru 0-250mm.

Din punct de vedere practic se recomanda ca la etalonarea scarii de masurare a distantelor sa se aleaga pe blocul de calibrare o anumita grosime pentru care va rezulta cel putin doua sau mai multe ecouri.

Pentru examinarea proportionalitatii distantelor se aseaza palpatorul pe blocul de calibrare A1, in zona cu grosimea de 25 mm, aparatul fiind pe domeniul de 250mm si se obtin ecouri. In cazul in care ecourile 2 si 8 ale scalei, ecourile intermediare nu trebuie sa depaseasca 1 diviziune din gradatiile scalei.

Pentru reglarea sensibilitatii se deosebesc doua cazuri. Primul caz este acela in care grosimea piesei este inferioara grosimii blocului de etalonare. Pentru acesta se fixeaza palpatorul pe blocul de calibrare si se obtine al doilea ecou cu o inaltime de h=50%. Se pune palpatorul pe piesa si se obtine al cincilea ecou cu h=50%.

Cand grosimea piesei este superioara rosimii blocului de etalonare al patrulea ecou obtinut prin fixarea palpatorului pe blocul A1 are inaltimea de 50% si corespunde cu aceasi inaltime a ecoului 2 pe piesa ce se examineaza. Trebuie mentionat ca la doua piese cu aceasi grosime ecourile nu au aceasi inaltime, datorita gradului de absorbtie a ultrasunetului, respectiv a atenuarii ultrasunetului in materialul examinat.

Puterea separatoare se poate determina si cu ajutorul blocului de calibrare A1, caz in care scala de masurare a distantelor va fi pe domeniul 0-100mm. Se fixeaza palpatorul pe suprafata etalonului cu lungimea de 300mm in zona in care se obtin ecouri de la distantele de 85,91 si 100 mm - deci ecouri ce difera ca distanta cu 6 si 9 mm. In cazul in care cele trei ecouri apar distincte pe ecran, se apreciaza ca puterea separatoare a palpatorului pentru zona 85-100mm este satisfacatoare.