Notiuni generale privind sistemele mecatronice

1. Notiuni generale privind sistemele automate

In ideea actionarii robotilor si manipulatoarelor, un rol important il ocupa optimizarea servoactionarilor pentru fiecare grad de mobilitate. In acest scop este strict necesar a se studia comportarea dinamica a servosistemelor prin prisma teoriei din automatica liniara si neliniara.

Un sistem automat reprezinta reuniunea a doua subsisteme: subsistemul tehnologic (instalatia tehnologica sau procesul de automatizat IT) si subsistemul de automatizare (dispozitivul de automatizare) care stabileste legea sau algoritmul de conducere al procesului dupa un program prestabilit.

Reprezentarea schemei bloc a unui sistem de reglare automata din figura 1, evidentiaza principalele marimi care intervin in cadrul functionarii sistemului in circuit inchis pentru cazul existentei unei singure intrari si a unei singure iesiri si anume:

i - marimea de referinta sau intrarea programatoare;

a - marimea de eroare sau de actionare;

c - marimea de comanda;

m - marimea de executie;

e - marimea de iesire;

ep - componenta marimii de iesire in absenta perturbatiei z;

ez - componenta marimii de iesire datorita perturbatiei z;

r - marimea de reactie;

z - intrarea perturbatoare sau perturbatia.

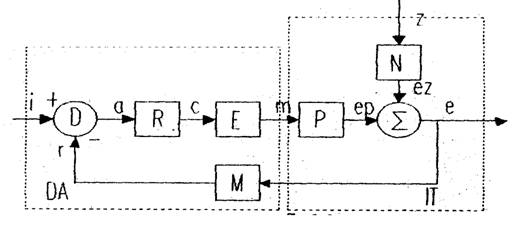
Fig. 1

Semnificatia notatiilor din figura 1 in conformitate cu STAS 6019-80, este:

D - element de comparatie, care realizeaza comparatia intre marimea de intrare si marimea de reactie;

R - regulator, care emite marimea de comanda c in functie de marimea de actionare a, de intrarea si derivarea in raport cu timpul acestuia;

E - element de executie;

P - procesul automatizat;

M - element de masurare (traductor sau adaptor);

N - ansamblul prin care perturbatia z produce marimea ez.

DA - dispozitivul de automatizare reprezinta ansamblul de aparate si legaturi care se conecteaza cu procesul in scopul realizarii operatiilor de comanda si de reglare dorite.

IT - instalatia tehnologica sau procesul automatizat reprezinta ansamblul transformarilor, caracterizat prin una sau mai multe marimi masurabile, pentru care se realizeaza o automatizare.

Comanda - este un ansamblu de operatii care se efectueaza in circuit deschis si care are ca efect, stabilirea unei dependente dupa o lege prestabilita, pentru valoarea unei marimi de iesire e dintr-un proces, in raport cu marimea de intrare i, independente de proces (comanda manuala, automata, secventiala sau cu program).

Reglarea - este un ansamblu de operatii care se efectueaza in circuit inchis, formand o bucla si care are ca efect:

fie stabilirea unei dependente dupa o lege prestabilita e=f(i);

fie reducerea influentei marilor perturbatoare de tip aditiv sau parametric asupra marimilor din proces, e=f(z).

In primul caz, sistemul automat se mai poate numi sistem de urmarire automata si are rolul de a garanta ca orice modificare i a marimii de intrare programatoare, chiar in conditiile unei transmisii nerigide, sa fie urmata de o modificare e, a carei valoare depinde exclusiv de marimea i si de structura dispozitivului de automatizare.

In cel de al doilea caz, sistemul automat se poate numi sistem de reglare automata sau de supraveghere si are rolul de a garanta ca orice modificare z a marimii de intrare perturbatoare, in acelasi conditii de nerigiditate a transmisiei, sa nu fie urmata decat de o perturbare pasagera a marimii de iesire e, dupa care, in regim stationar, variabila marimii de iesire e, sa devina nula.

Obtinerea unor modele matematice cat mai aproape de comportarea reala a modelului fizic a sistemului de reglare automata, reprezinta etapa cea mai importanta si cea mai dificila care se impune a fi rezolvata.

Calitatea analizei si sintezei servosistemelor este determinata de precizia cu care se aproximeaza functionarea modelului fizic.

Modelul matematic aferent functionarii unui servosistem reprezinta cea mai generala caracterizare a acestuia. Modelul matematic poate fi stabilit prin metode analitice sau prin metode experimentale.

In cazul modelarii analitice a servosistemelor, modelele matematice sunt obtinute pe baza unor legi generale, dintre acre mentionam:

legea de conservare a impulsului;

legea conservarii momentului cinetic ;

legea lui Kirchhoff pentru nodurile de retea electrica, hidraulica sau pneumatica ;

legea lui Kirchhoff pentru ochiurile de retea electrica, hidraulica sau pneumatica

;

legea conservarii masei ;

legea conservarii energiei ;

Modelarea servosistemelor pe baza identificarii experimentale consta in determinarea unui model matematic pe baza masurarilor variabile de intrare si iesire. Modelarea pe baza unor perechi de valori se efectueaza utilizand metode de aproximare de tipul:

polinomul de interpolare a lui Lagrange

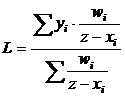(1)

polinomului de aproximare prin metoda celor mai mici patrate de forma

(2)

functiilor de interpolare cubice, de forma:

(3)

Modelele matematice aferente comportarii dinamice a unui servosistem sau element component al acestuia pot fi, sub forma de ecuatii diferentiale, functii de transfer sau caracteristici de frecventa.

2. Analiza si sinteza servosistemelor

Prin analiza unui servosistem se intelege identificarea si modelarea servosistemului, urmata de determinarea pe baza analizei parametrilor caracteristici generalizati si a performantelor caracteristice, a parametrilor constructivi- functionali, cu influenta prioritara asupra comportarii dinamice.

Analiza performantelor evidentiaza gradul de precizie cu care se realizeaza relatia dorita intre intrarea si iesirea sistemului automat, precum si influenta anumitor parametri ai sistemului asupra performantelor sale.

Prin sinteza unui servosistem se intelege, proiectarea servosistemului, functie de scopul propus, proiectare care include, stabilirea si proiectare regulatoarelor, a corectiilor, alegerea traductoarelor de reactie, alegerea parametrilor constructivi-functionali, in scopul imbunatatirii parametrilor caracteristici generalizati, precum si a performantelor servosistemului.

Sinteza unui servosistem presupune:

stabilirea criteriilor de performanta pentru sistem, pornind de la consideratiile si restrictiile impuse;

intocmirea schemei structurale a sistemului automat cu evidentierea tuturor elementelor;

alegerea corespunzatoare a sistemului automat cu evidentierea tuturor elementelor componente;

alegerea corespunzatoare a elementelor de masura si a elementelor de executie;

alegerea si acordarea optima a regulatorului automat in vederea satisfacerii criteriilor de performanta impuse aprioric;

verificarea prin analiza a performantelor realizate de modelul proiectat.

In cazul in care anumite performante ale sistemului proiectat si analizat, nu au fost realizate, se trece la reproiectarea lui sau introducerea corectiilor cu scopul imbunatatirii performantelor numai pe anumite domenii de frecventa.

Corectiile reprezinta elementele suplimentare introduse in structura unui servosistem, cu scopul imbunatatirii performantelor comportarii dinamice in anumite domenii de frecventa, conform cerintelor din tema de proiectare.

Corectia poate fi realizata fie prin modificarea unor parametri constructivi-functionali a caror influenta a fost deja determinata cu ocazia analizei efectuate, fie prin modificarea parametrilor regulatorului determinat pe baza unuia dintre criteriile impuse de performantelor dinamice cuprinse in tema de proiectare, fie prin introducerea unor elemente compensatoare alese astfel incat sa asigure obtinerea performantelor dinamice impuse.

3. Modelarea matematica a sistemelor

Modelul matematic al uni sistem automat este constituit dintr-un ansamblu de ecuatii algebrice si diferentiale, care exprima cel mai fidel variatia in timp a unei marimi de iesire, functie de o anumita marime de intrare.

Pentru obtinerea modelului matematic trebuie parcurse urmatoarele etape:

se descompune sistemul dinamic in componentele de baza sau in elemente a caror modelare este mai simplu de efectuat, incercandu-se echivalarea acestora cu elemente liniare sau liniarizabile pe portiuni;

se scriu relatiile caracteristice ale fiecaruia dintre aceste elemente dinamice, cautandu-se a se exprima matematic cat mai fidel fenomenele fizice care guverneaza comportarea dinamica a cestora;

se scriu relatiile privind conexiunile dintre elementele dinamice, care rezulta din insasi etapa anterioara. Aceste relatii sunt regula de tipul relatiilor lui Kirchhoff scrise atat pentru noduri cat si pentru ochiuri;

din ansamblul relatiilor determinate in cadrul punctelor 2 si 3, se incearca a se obtine o ecuatie unica, intre marimea de intrare si marimea de iesire, ecuatie liniara sau liniarizabila pe portiuni.

Modelul matematic exprimat sintetic sub forma unei singure ecuatii va avea forma:

(4)

4. Liniarizarea modelelor matematice neliniare

Majoritatea sistemelor dinamice reale conduc la modele matematice neliniare. Experimental, sistemele neliniare pot fi usor deosebite de cele liniare, prin determinarea raspunsului la dublarea semnalului de intrare, la excitarea cu un semnal tip treapta.

Daca amplitudinea semnalului de iesire nu se dubleaza ci capata o valoare oarecare, servosistemul este neliniar.

Liniarizarea modelului matematic cuprinde:

a)         liniarizarea modelului matematic al fiecarei componente prin dezvoltare in serie Taylor sau liniarizarea pe portiuni in jurul unor puncte de functionare cu introducerea coeficientilor de corectie;

b)         asimilarea unor modele matematice cu functii neliniare elementare des uzitate si liniarizarea acestora, functie de tipul fiecareia.

Liniarizarea modelului matematic in jurul unor puncte de functionare.

Se considera functia de doua variabile f(x,y), care trebuie liniarizata intr-un punct de functionare cunoscut x₀y₀. Se calculeaza derivata totala a functiei in punctul de functionare cunoscut:

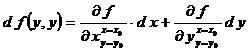(5)

Daca se renunta la diferentiala, functia liniarizata se scrie astfel:

(6)

unde, k₁ si k₂ reprezinta coeficientii de liniarizare.

In scopul realizarii corectiei functiei liniarizate, pentru a obtine aceeasi valoare in punctul de functionare atat pentru functia initiala cat si pentru cea liniarizata, se introduc coeficientii de liniarizare,

Acesti coeficienti au expresiile:

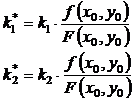(7)