PROIECTAREA MECANISMELOR DE PUTERE ALE PUNtii MOTOARE

1. Generalitati

Rotile automobilului, in functie de natura, sensul si marimea fortelor si momentelor care actioneaza asupra lor, pot fi:

-roti motoare (antrenate): sunt rotile care ruleaza sub actiunea fluxului de putere primit prin intermediul transmisiei de la motorul automobilului;

-roti libere (conduse): sunt rotile care ruleaza sub actiunea unei forte de impingere sau tragere, de acelasi sens cu sensul vitezei de deplasare a automobilului, exercitata asupra lor de cadrul sau caroseria automobilului;

-roti franate: sunt rotile care ruleaza sub actiunea unui moment de franare dezvoltat in mecanismele de franare ale rotilor (franare activa), sau de catre grupul motopropulsor in regim de mers antrenat (frana de motor).

Pentru autoturisme, prevazute cu doua punti, organizarea tractiunii se poate realiza dupa solutiile 4x2 sau 4x4, prima cifra indicand numarul rotilor, iar cea de-a doua, pe cel al rotilor motoare. Pentru organizarea tractiunii de tipul 4x2, puntea motoare poate fi dispusa in fata sau in spate, iar pentru tipul 4x4 ambele punti sunt cu roti motoare.

Puntile motoare, fata de cele nemotoare, asigura transferul fluxului de putere pentru autopropulsare, functie de modul de organizare a tractiunii, de la arborele secundar al cutiei de viteze sau de la transmisia longitudinala, la rotile motoare. De-a lungul acestui transfer, fluxul de putere sufera o serie de adaptari si anume:

• adaptare geometrica determinata de pozitia relativa dintre planul in care se roteste arborele cotit al motorului si planul in care se rotesc rotile motoare;
• adaptare cinematica determinata de asigurarea rapoartelor de transmitere necesare transmisiei automobilului;
• divizarea fluxului de putere primit in doua ramuri, cate unul transmis fiecarei din rotile motoare ale puntii.

Pentru a-si indeplinii functiile de mai inainte mecanismele fluxului de putere din puntea motoare cuprind: transmisia principala (sau angrenajul principal), diferentialul si transmisiile la rotile motoare.

In procesul autopropulsarii, din interactiunea rotilor motoare cu calea, iau nastere forte si momente de reactiune. Puntea are rolul de a prelua toate aceste forte si momente si de a le transmite elementelor elastice ale suspensiei si cadrului sau caroseriei automobilului. Preluarea fortelor si a momentelor, precum si transmiterea lor dupa directii rigide cadrului sau caroseriei automobilului, se face de un ansamblu constructiv al puntii, numit mecanismul de ghidare a rotilor. Mecanismul de ghidare defineste, in ansamblul puntii, cinematica rotii suspendate elastic prin intermediul suspensiei. Se definesc astfel punti rigide, puntile la care prin oscilatia unei roti fata de caroserie pozitia relativa dintre roti ramane nemodificata (punti cu oscilatia dependenta a rotilor), si punti articulate, puntile la care oscilatia unei roti fata de caroserie determina modificarea pozitiei relative dintre rotile puntii (punti cu roti independente).

Legatura in punte dintre mecanismele fluxului de putere si mecanismul de ghidare se face prin butucul rotii.

2.Transmisia principala

Transmisia principala cuprinde toate mecanismele din punte care realizeaza o demultiplicare a turatei motorului.

Rolul transmisiei principale este de a mari momentul motor primit de la transmisia longitudinala sau de la arborele primar al cutiei de viteze si de a-l transmite, prin intermediul diferentialului si arborilor planetari, la rotile motoare, ce se rotesc in jurul unei axe dispuse sub un unghi de 90⁰ fata de axa longitudinala a automobilului.

Amplificarea momentului motorului, cu un raport de transmitere de regula constant, numit raportul de transmitere al puntii motoare (notat i_o), reprezinta adaptarea cinematica necesara impusa de conlucrarea motor-transmisie. Pentru a realiza aceasta functie, prin constructie transmisiile principale sunt mecanisme de tipul angrenajelor. La autoturisme, la care valoarea necesara a raportului de transmitere este cuprinsa in intervalul de valori 35, transmisia principala este constituita dintr-un singur angrenaj. Astfel de transmisii principale se numesc transmisii principale simple.

Adaptarea geometrica a fluxului de putere pentru autopropulsare presupune directionarea lui de la axa in jurul careia se roteste arborele cotit al motorului la axa transversala a automobilului, in jurul careia se rotesc rotile motoare. Aceasta functie se realizeaza in transmisia principala prin tipul angrenajului utilizat si anume angrenaje cu axe ortogonale in cazul dispunerii longitudinale a motorului si angrenaje cu axe paralele la dispunerea transversala a motorului.

2.1. Constructia transmisiei principale

La automobilele la care motorul este dispus longitudinal, pentru constructia transmisiei principale se utilizeaza angrenaje de tipul cu roti dintate conice sau hipoide, iar la automobilele cu motorul dispus transversal, angrenaje cu roti dintate cilindrice.

In figura 1 este reprezentata schema cinematica de organizare a unei transmisii principale simple cu roti dintate conice.

Elementul conducator al angrenajului este pinionul de atac 2, iar elementul condus este roata dintata 3, cu care se afla permanent in angrenare. Fluxul de putere este primit de pinion prin arborele 1 si flansa 9 de la transmisia longitudinala in cazul organizarii clasice a transmisiei, sau direct de la arborele secundar al cutiei de viteze, cu care este realizat corp comun, in celelalte moduri de organizare a transmisiei. Roata condusa 3, numita si coroana diferentialului, este solidarizata prin suruburile 6 de carcasa diferentialului 7, caruia ii transmite fluxul de putere, de unde, divizat acesta este transmis mai departe prin arborii 8 spre rotile motoare. Intreg ansamblul este montat, prin lagare cu rulmenti in carterul 4, numit carterul puntii motoare.

In afara realizarii conditiilor de adaptare cinematica si geometrica a fluxului de putere, pentru asigurarea calitatilor functionale, in transmisia principala se prevad o serie de solutii constructive privind tipul danturii, rigiditatea constructiei, compensarea uzurilor si pozitionarea relativa a rotilor.

Dintre tipurile de danturi ale rotilor conice, generalizare au primit-o angrenajele conice cu dantura curba. Dantura curba, fata de celelalte tipuri de danturi, asigura:

o       la rapoarte de transmitere egale, dimensiuni de gabarit de pana la de doua ori mai mici (numarul minim de dinti ai pinionului poate fi redus la 7.9, fata de minimum 13 cat este la celelalte doua tipuri);

o       cresterea gradului de acoperire, ceea ce se traduce in functionare mai linistita si durabilitate sporita;

o       diminuarea sensibilitatii la deplasari relative ale rotilor, ca urmare a deformatiilor elastice ale ansamblului in timpul functionarii, prin posibilitatea eliminari concentratorilor de tensiune prin procedee tehnologice simple;

Dintre transmisiile principale cu dantura curba, cea mai larga raspandire o au cele cu dantura in arc de cerc, cunoscuta sub numele de dantura Gleason, aceasta bucurandu-se si de avantajul prelucrarii danturii pe masini-unelte de mare precizie. Dezavantajul principal al angrenajelor cu dantura in arc de cerc il constituie prezenta unor eforturi axiale mari, care isi schimba sensul la schimbarea sensului de deplasare al automobilului. Avand in vedere ca aceasta situatie este de scurta durata, atat sensul cat si valoarea fortelor axiale sunt acceptabile.

Angrenajele conice sunt foarte sensibile in ceea ce priveste conditiile de montaj, in sensul asigurarii angrenarii corecte. In cazul cand varfurile conurilor celor doua roti nu coincid, diferenta fiind de ordinul zecimilor de milimetri, apar concentrari de forte pe muchiile dintilor, cresc brusc tensiunile de contact si solicitarile de incovoiere, cresc zgomotul, incalzirea , uzura acestora si se mareste considerabil probabilitatea distrugerii angrenajului. Chiar si in cazul unei fabricatii si montaj corecte, calitatea angrenarii poate fi compromisa ca urmare a deformarii pieselor transmisiei si uzarii rulmentilor.

Pentru elementele angrenajului conic, valorile deformatiilor admise sunt date in figura 2. Asigurarea rigiditatii necesare este determinata de modul de montare in carterul puntii a pinionului de atac, de tipul rulmentilor utilizati si de unele masuri constructive.

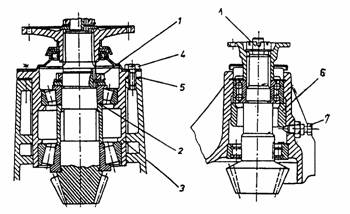
Pentru pinionului de atac se utilizeaza doua solutii de rezemare si anume intre reazeme si in consola. Cu toate ca, in cazul utilizarii unui montaj intre reazeme, rigiditatea transmisiei principale creste de peste 30 de ori decat la montajul in consola la autoturisme, determinat de constructia carterului puntii motoare, se utilizeaza rezemarea in consola. In figura 3 sunt prezentate solutii de montare a pinionului de atac. Pentru a se micsora deformatiile axiale, se utilizeaza rulmenti cu role conice cu unghi cat mai mare de deschidere a conului. Pentru marirea lungimii efective a lagarului si pentru sporirea rigiditatii radiale a pionului, rulmenti se monteaza in "0" (fig.3,a). In acelasi scop sunt indicati rulmentii radiali cu doua randuri de bile, sau rulmenti radiali cu role, deoarece au o mare rigiditate radiala(fig.3, b).

In toate cazurile, deformatiile axiale pot fi reduse printr-o strangere preliminara pe directia axiala a pieselor montate pe arborele pinionului de atac. Aceasta strangere conduce la anularea jocurilor axiale din lagare si la aparitia unor deformatii elastice ale rulmentilor. Valoarea strangerii initiale se accepta in limitele 0,005.0,07 mm si se apreciaza prin marirea momentului necesar insurubarii piulitelor de reglare (1,5.2,0 Nm la pinionul montat in consola). Valoarea definitiva a prestrangerii se stabileste in urma incercarilor experimentale pe prototipuri. Odata cu cresterea prestrangerii se micsoreaza posibilitatea de perturbare a angrenarii rotilor conice si se imbunatatesc conditiile de functionare a rulmentilor, deoarece se asigura o distributie mai uniforma a sarcinilor pe bile sau role si se reduc solicitarile dinamice provocate de schimbarea marimii si sensului fortelor din angrenajul conic. Marirea strangerii peste o valoare optima, recomandata de constructor, conduce la o sporire a uzurii lagarelor.

a) b)

Fig.3. Solutii de montare a pinionului de atac

Pentru realizarea prestrangerii (fig.3,a) se utilizeaza piulitele 1 (cu sisteme de asigurare a pozitiei) de pe arborii pinioanelor de atac. Saibele calibrate 2, dintre inelele interioare ale rulmentilor servesc la reglarea jocului acestora. La constructiile recente de autoturisme s-a renuntat la solutia de mai inainte, inlocuindu-se saibele de reglaj cu o bucsa deformabila montata intre cei doi rulmenti, sau intre rulmentul dinspre flansa pinionului si un umar al acestuia.

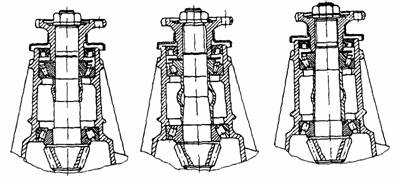
In figura 4 sunt prezentate solutiile de pretensionare cu bucsa elastica (1), utilizate de cateva firme constructoare de autoturisme de teren.

a) b) c)

Fig.4. Solutii de pretensionare a lagarelor pinionului de atac:

a-- Lada Niva; b-Suzuki Vitara; c-Ford, Mercedes, ARO

Avantajul acestei solutii consta in aceea ca pretensionarea rulmentilor se asigura de la primul montaj, facand posibila automatizarea acestuia. In plus, pretensionarea initiala este mentinuta constanta timp indelungat.

Montarea coroanei dintate a angrenajului conic in carterul puntii, prin intermediul carcasei diferentialului, se face in cele mai frecvente cazuri prin rulmenti cu role conice. Pentru reducerea lungimii efective dintre reazeme, rulmentii sunt montati in "X" (fig. 5).

In figura 6 este prezentata constructia a doua transmisii principale simple cu angrenaje de roti dintate conice. Constructia din figura 6,a, pentru un autoturism cu punte rigida, are pinionul de atac 1 montat in consola prin rulmentii 2 direct in carterul 3 al transmisiei principale. Reglarea pinionului si pozitionarea axiala a acestuia fata de coroana 16 se realizeaza prin saibele 8, piesele fiind stranse de piulita 5 prin flansa Prin flansa 6, transmisia principala primeste fluxul de putere al motorului de la transmisia longitudinala. Etansarea lagarului este asigurata de deflectoarele 7 si 9 si de inelul 4. Coroana dintata 16 se fixeaza prin prezoanele 14 de carcasa 15 a diferentialului. Ansamblul de rulmenti 11 este fixat de carter prin intermediul semilagarelor 13. Reglarea coroanei se face cu ajutorul piulitelor 10, asigurate in pozitia reglata de sigurantele basculante 12. Constructia din figura 6,b, asemanatoare constructiei de mai inainte, este destinata unui autoturism cu punte cu roti independente, cand transmisia principala impreuna cu diferentialul sunt dispuse pe masa suspendata a automobilului.

Din categoria angrenajelor conice cu dantura curba fac parte si angrenajele hipoide (angrenajele hipoide cu axe geometrice incrucisate, dispuse in planuri diferite). In raport cu alte tipuri de angrenaje, angrenajele hipoide prezinta o serie de avantaje:

- au capacitate mare de transmitere a efortului, datorita atat formei dintilor, cat si configuratiei geometrice a ansamblului, care permite constructia unor lagare rigide;

- metodele de prelucrare existente permit obtinerea unui contact liniar intre dinti, respectiv posibilitatea controlului lungimii petei de contact, ceea ce aduce un plus de crestere a capacitatii portante;

- datorita alunecarii intre dinti (in lungul dintelui), angrenajele hipoide functioneaza mai linistit decat angrenajele conice cu dinti curbi;

- tehnologia de executie a rotilor hipoide este, in principiu, aceeasi ca cea a rotilor conice cu dantura curba, prelucrarea facand-se pe aceleasi utilaje.

La folosirea angrenajelor hipoide trebuie sa se tina seama de faptul ca prezenta alunecarii intre dinti, mult mai mare ca la angrenajele conice, creeaza

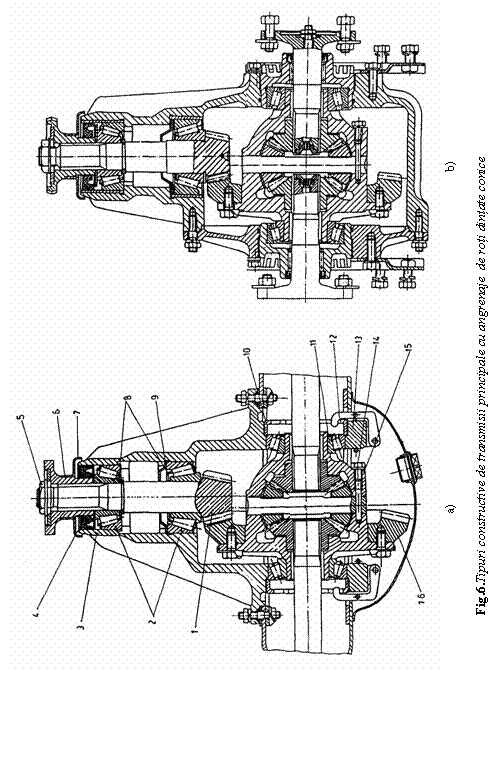
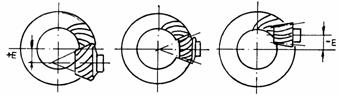
tendinta spre o uzura mai pronuntata de abraziune, decat la oboseala. Pentru aceasta sunt necesare masuri suplimentare legate de calitatea suprafetelor dintilor, care in acest caz trebuie sa aiba duritate mai mare, iar pentru ungere sa se utilizeze uleiuri corespunzatoare unor presiuni de contact mari si viteze de alunecare sporite. La angrenajele hipoide, figura 7, axa pinionului se poate gasi sub axa coroanei -deplasarea axei pinionului fiind in sensul spirei coroanei (deplasare hipoida pozitiva, (fig.7,a), sau deasupra axei pinionului - deplasarea axei pinionului fiind in contrasensul spirei coroanei (deplasare hipoida negativa - fig.7,c). In figura 7, b este prezentat angrenajul conic echivalent.

a) b) c)

Fig.7. Angrenaje hipoide:

a-deplasare hipoida pozitiva; b-angrenaj conic echivalent; c-deplasare hipoida negativa

In legatura cu pozitia reciproca pinion-coroana se precizeaza ca la deplasarea hipoida pozitiva (+E), pasul frontal al pinionului va fi mai mare decat pasul frontal al coroanei, iar la deplasarea hipoida negativa (-E), pasul va fi mai mic. Corespunzator acestor doua situatii, diametrul pinionului va rezulta mai mare sau mai mic decat al pinionului conic de referinta (echivalent). Din motive de crestere a capacitatii portante a angrenajului pentru automobile, angrenajul hipoid se foloseste in toate cazurile in forma in care deplasarea aduce o marire a diametrului pinionului.

Constructia unei transmisii principale cu angrenaj hipoid este prezentata in figura 8.

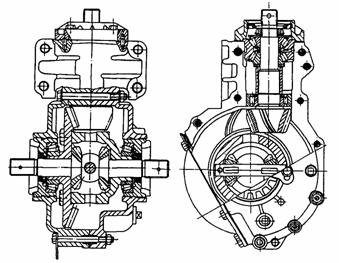
Fig.8. Constructia transmisiei principale cu angrenaj hipoid

La automobilele organizate dupa solutia "totul spate", sau "totul fata", cu motorul dispus longitudinal, transmisia principala si cutia de viteze sunt organizate intr-un carter comun (fig. 9), cu dispunerea transmisiei principale si a diferentialului intre carterul ambreiajului si cutia de viteze. La transmisia principala, compusa din pinionul 2 si coroana 3 a diferentialului, pinionul de atac 2, avand dimensiuni constructive apropiate de cele ale arborelui secundar 1 al cutiei de viteze, se executa corp comun cu acesta, in capatul arborelui.

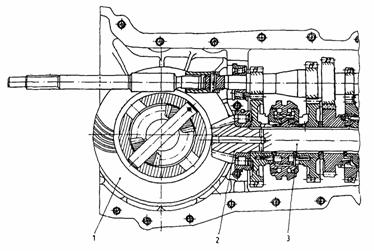
Fig. Constructia transmisiei principale la autoturismele

de tipul "totul fata" cu dispunerea longitudinala a motorului

Cand motorul este dispus transversal, transmisia principala este organizata sub forma unui angrenaj de roti cilindrice 1 si 2 cu axe fixe (fig.10). Pentru sporirea rigiditatii arborilor cutiei de viteze si pentru deplasarea carterului puntii motoare spre axa longitudinala a automobilului, pinionul 1 al transmisiei principale se executa corp comun cu arborele secundar, in capatul din consola al arborelui secundar. Coroana cilindrica 2 a diferentialului, impreuna cu diferentialul, sunt dispuse in carterul puntii, plasat in zona ambreiajului. Deoarece utilizarea angrenajului cilindric determina forte axiale mult mai mici fata de angrenajele conice sau hipoide, pentru rezemarea coroanei, prin lagarele diferentialului, se utilizeaza de regula rulmenti radiali axiali cu bile.

La transmisiile principale care au pinionul de atac solidar cu arborele secundar al cutiei de viteze, pentru descarcarea rulmentilor arborelui secundar de fortele axiale din angrenajele cu dinti inclinati ale mecanismului reductor al cutiei de viteze se adopta pentru sensul inclinarii dintilor pinionului acelasi sens ca pentru rotile dintate din cutia de viteze.

Elemente de calculul transmisiei principale

Calculul transmisiei principale cuprinde calculul de dimensionare si verificare a angrenajelor de roti dintate, de dimensionare si verificare a arborilor si a rulmentilor.

a. Determinarea momentului de calcul. Pentru automobile cu o punte motoare momentul de calcul M_c se considera momentul maxim al motorului M_M, redus la angrenajul calculat prin relatia relatia:

, (1)

in care: i_cv1 este raportul de transmitere al cutiei de viteze in prima treapta; este randamentul transmisiei de la motor la angrenajul calculat.

Pentru automobile cu mai mult de o punte motoare, cand distributia momentului motor nu este precizata, momentul de calcul se determina prin reducerea la transmisia principala a momentului capabil la roti prin aderenta cu ajutorul relatiei:

, (2)

unde: Z este reactiunea dinamica normala la puntea calculata; j_max =0,7.0,8- coeficientul de aderenta; r_d- raza dinamica a rotii motoare; i₀-raportul de transmitere al transmisiei principale; - randamentul transmisiei de la rotile motoare la angrenajul transmisiei principale calculate.

b. Indicatii privind calculul de rezistenta si dimensionare al angrenajelor de roti dintate conice. Variatia inaltimii dintilor rotilor dintate conice determina o rigiditate variabila in lungul dintilor si, de aici, o distributie neuniforma a sarcinii.

Experienta a confirmat ca in calculele de rezistenta se obtin rezultate satisfacatoare daca se considera rezistenta rotii conice egala cu rezistenta unei roti cilindrice avand urmatoarele caracteristici: diametrul cercului de rostogolire egal cu diametrul cercului de rostogolire al rotii conice in sectiunea medie a dintelui; modulul corespunzator modulului rotii conice in aceeasi sectiune; profilul dintilor corespunzator profilului dintilor rotii echivalente. Roata echivalenta se obtine prin desfasurarea conului mediu pe un plan. Numarul de dinti al rotilor echivalente ale angrenajului conic se determina cu relatiile:

; (3)

in care: z₁este numarul de dinti ai pinionului de atac; z₂- numarul de dinti ai coroanei; d₁ si d -unghiul conului de divizare al pinionului, respectiv al coroanei (tab. 1); b_m-unghiul mediu de inclinare al dintilor.

Tabelul 1

Calculul parametrilor angrenajelor conice cu dinti drepti si curbi

Rotile de inlocuire fiind elemente imaginare de calcul, se lucreaza pentru numerele de dinti ai rotilor echivalente cu numerele fractionare rezultate din calcul.

Pe baza acestor considerente, prin analogie cu relatiile de calcul stabilite pentru rotile dintate cilindrice (v. cap.2-cutii de viteze), se poate efectua calculul de dimensionare si verificare la uzura al rotilor dintate conice.

La angrenajele conice se standardizeaza modulul frontal (m_f), intre modulul frontal si modulul normal mediu determinat din asimilarea angrenajului conic cu unul cilindric existand relatia :

, (4)

in care b este latimea de lucru a danturii. Pentru latimea de lucru a danturii se recomanda b=(6.8)^.m_med.

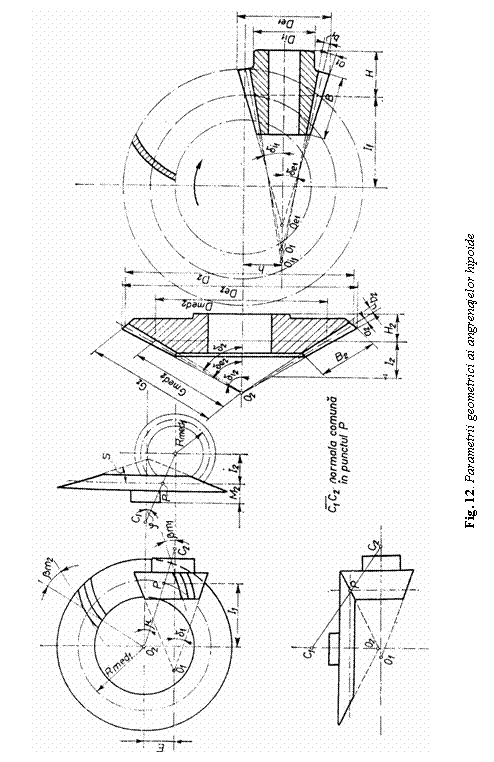
Parametrii geometrici pentru angrenajele conice cu dinti drepti sau curbi, utilizand notatiile din figura 11, sunt prezentati in tabelul 2. Determinarea dimensiunilor conform acestui tabel presupune cunoasterea unor date initiale stabilite din conditii cinematice si constructive, dupa cum urmeaza:

-numarul de dinti al pinionului si al coroanei z₁ si z_2;

-modulul frontal la diametrul mare m_f;

-unghiul de inclinare al spirei dintelui pe cercul mediu b_m

-unghiul de angrenare in sectiune normala a_n

c. Indicatii privind calculul de rezistenta si dimensionare al angrenajelor hipoide. La angrenajele hipoide, pentru aceeasi valoare a razei medii de divizare a coroanei, exista un numar mare de variante ale angrenajului hipoid. Proiectantul trebuie sa determine grupul de angrenaje care satisfac conditia constructiva (z₁, z₂, D_d2 si E), iar in final sa aleaga acel angrenaj la care raza de curbura a dintilor corespunde posibilitatilor de reglaj ale unui cap portcutite existent la masina de danturat si unei valori a unghiului Da (unghiul dintre axa cinematica si axa geometrica a danturii), corespunzatoare sculelor existente sau posibil de realizat, bineinteles cu respectarea unghiurilor medii de inclinare b_med si b_med , spre a mentine fortele ce actioneaza in lagare in jurul valorilor fortelor axiale din lagarele arborelui secundar datorate angrenajelor de roti dintate ce formeaza treptele cutiei de viteze. In aceste conditii dimensionarea rotilor componente solicita un volum mare de calcule, datorita necesitatii de a se calcula prin tatonari un numar mare de angrenaje, din care se alege unul corespunzator.

Pentru aceasta, calculul se desfasoara iterativ, dupa metode specifice dezvoltate in organe de masini. In aceste conditii, pentru predimensionarea transmisiilor principale simple cu angrenaje hipoide se prezinta o metoda simplificata de calcul, in care calculul de rezistenta al danturi hipoide se poate face dupa indicatiile de la angrenajele conice.

Deplasarea hipoida E se determina in functie de diametrul de divizare exterior al coroanei (rotii conduse a angrenajului) cu relatia:

E 0,2D_d2 (5)

Daca M_c este momentul de calcul exprimat in Nm, diametrul de divizare D_d2 se apreciaza orientativ cu relatia:

(6)

Latimea B a coroanei se determina cu relatia:

(7)

in care G₂ este lungimea maxima a generatoarei conului de divizare al rotii conduse. Valorile inferioare se aleg pentru coroane cu diametre mari, iar cele superioare pentru coroane cu diametre mici.

La angrenajele hipoide, in afara calculului indicat mai inainte, se face verificarea la incarcarea specifica pe 1 cm de latime a coroanei cu relatia:

(8)

Daca M_c s-a calculat cu relatia (1), incarcarea specifica admisibila nu trebuie sa depaseasca 1150 Mpa, iar daca M_c s-a calculat cu relatia (2), incarcarea specifica admisibila are valorile de 600-750 MPa.

Parametrii geometrici pentru angrenajele hipoide, utilizand notatiile din figura 12, sunt prezentati in tabelul 4.

Tabelul 2: Calculul parametrilor geometrici ai angrenajelor hipoide

cu dinti in arc de cerc si cu inaltime variabila

Tabelul 2 (continuare)

d. Indicatii privind calculul de dimensionare si verificare a arborilor si lagarelor. Calculul arborilor transmisiilor principale cuprinde: determinarea schemei de incarcare a arborilor, calculul reactiunilor, calculul momentului de torsiune si incovoiere, determinarea diametrului si verificarea la rigiditate.

Pentru calculul fortelor transmise la arbori de catre rotile in angrenare se considera forta normala de angrenare F_n care actioneaza la mijlocul dintilor (fig. 13) cu cele trei componente: tangentiala F_t, radiala F_r, si axiala F_a.

Forta normala si componentele ei dupa cele trei directii se calculeaza cu relatiile din tabelul 3. La danturi conice drepte, componenta radiala F_r actioneaza spre axa rotii, iar cea axiala F_a , dinspre varful conului de divizare spre roata. La danturi conice inclinate sau curbe, functie de anumiti parametri geometrici, componentele F_r si F_a pot avea si sensuri negative (tabelul 3).

Pentru deplasarea inainte a automobilului cu inclinare spre dreapta a dintelui pinionului de atac, schema de incarcare a arborilor pentru determinarea reactiunilor din lagare este prezentata in tabelul 10. Pentru calculul reactiunilor din 1agarele de montare in carterul transmisiei principale se utilizeaza relatii analoage celor stabilite la calculul reactiunilor din lagarele arborilor cutiilor de viteze.

Pentru calculul reactiunilor axiale care actioneaza asupra rulmentilor cu role conice se folosesc, functie de tipul montajului utilizat, relatiile din tabelul 4.

Coeficientii y, functie de limita raportului , au valorile y=0 pentru , si y=0,4^.ctg a, pentru , unde: F_a este forta axiala din arbore; R - rezultanta geometrica a reactiunilor Z si Y (tabelul 5); a - unghiul nominal de contact (unghiul dintre directia de actionare a sarcinii pe bile si un plan perpendicular pe axa rulmentului).

Pentru verificarea rigiditatii transmisiei principale, pe baza schemelor din tabelul 4, se procedeaza ca la arborii din cutiile de viteze. Sagetile obtinute se compara cu limitele recomandate (v. fig. 2). Avand reactiunile din lagare, se poate face calculul pentru alegerea rulmentilor dupa metoda prezentata la cutia de viteze.

Tabelul 3

Relatii pentru calculul fortelor din angrenajele ortogonale de roti dintate

Tabelul 4

Schema pentru calculul reactiunilor din lagarele transmisiei principale

Tabelul 5

Relatiile de calcul pentru fortele axiale care actioneaza asupra

rulmentilor cu role conice

3. Diferentialul

3.1. Constructia diferentialului

In constructia diferentialelor se disting mai multe solutii, grupate astfel:

. dupa caracteristicile cinematice se deosebesc diferentiale simetrice si diferentiale asimetrice;

. dupa caracteristicile dinamice, exprimate prin marimea frecarii interne, diferentialele pot fi: diferentiale simple, diferentiale blocabile si diferentiale autoblocabile;

In afara utilizarii diferentialului ca mecanism al puntii motoare, in constructia de automobile diferentialul se foloseste si ca mecanism divizor de flux la automobilele de tipul 4x4 (cap.4).

Deoarece diferentialele asimetrice si cele blocabile si autoblocabile sunt specifice autoturismelor de tipul 4x4, prezentarea acestora este facuta in cap.7.

In figura 14 se prezinta solutii constructive de diferentiale cu roti dintate conice. Carcasa 4 a diferentialului (fig.14, a), solidara de coroana dintata 2 a transmisiei principale, se roteste datorita miscarii primite de la transmisia principala. In carcasa sunt dispusi satelitii 3 si 6 care angreneaza in permanenta cu 2 roti planetare, fiecare comuna cu cate unul din arborii planetari 1 si Fixarea satelitilor in carcasa se face prin boltul 7. Pentru a asigura o centrare buna si o angrenare corecta a satelitilor cu rotile planetare, la constructia din fig.14, b suprafata frontala a satelitilor este sferica.

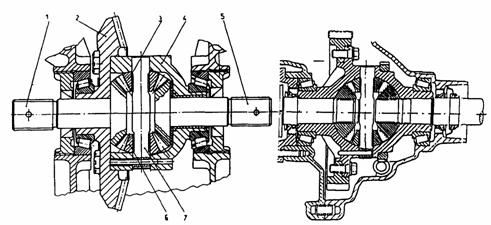a)    b)

Fig. 14. Constructia diferentialului simplu cu roti dintate conice

Constructiv, functie de tipul si de destinatia automobilului, satelitii sunt in numar de 2 sau de 4, montati echidistant pe cercul de rostogolire al pinioanelor planetare. Acest montaj asigura anularea sarcinilor radiale in pinioane si reducerea dimensiunile rotilor dintate prin marirea numarului de dinti aflati simultan in angrenare. Elementele componente ale unui diferential cu patru sateliti sunt prezentate in figura 1

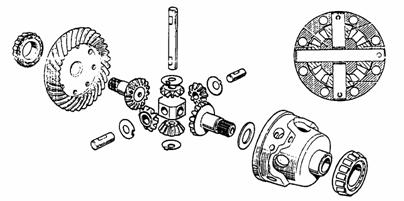
Fig. 1 Elementele componente ale diferentialului cu patru sateliti

si cu angrenaje de roti dintate conice

In figura 16 se reprezinta schema cinematica si constructia unui diferential simplu cu roti dintate cilindrice. Satelitii cilindrici 3 si 4, angrenati intre ei, sunt simultan in angrenare - primul 3 cu roata planetara 1, iar al doilea 4 cu roata planetara 2. Elementul conducator al diferentialului este carcasa 5, care este antrenata de transmisia principala. Constructiv, aceste diferentiale sunt realizate cu 4 sau cu 6 sateliti montati pereche.

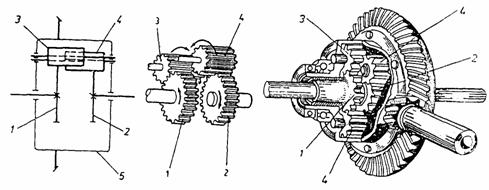
Fig. 16. Organizarea cinematica si constructia

diferentialului cu roti dintate cilindrice

3.4. Elemente de calculul diferentialului

Calculul de rezistenta al diferentialelor cuprinde calculul rotilor planetare, calculul satelitilor si al axelor satelitilor.

Pentru calculul organologic este necesar sa se stabileasca, pe baza fluxului de putere care circula prin elementele diferentialului, momentele de calcul. In figura 17 este reprezentata schema fluxului de puteri intr-un diferential simetric cu roti dintate conice, cand

Puterile corespunzatoare din diferential sunt:

P=- puterea transmisa de transmisia principala carcasei diferentialului (M_M este momentul maxim al motorului; i_cv1 - raportul de transmitere al cutiei de viteze in prima treapta de viteze; i_o - raportul de transmitere al transmisiei principale);

P - puterea de frecare transmisa de arborele in avans carcasei diferentialului;

P - puterea de frecare transmisa de carcasa arborelui planetar intarziat;

P'= - puterea transmisa de carcasa axelor satelitilor;

- puterea transmisa arborelui planetar intarziat;

- puterea transmisa arborelui planetar in avans.

Pentru diferentialele cu proprietati de blocare simetrice (), fluxul de putere care circula prin angrenajele de roti dintate este egal cu fluxul de putere primit de carcasa de la transmisia principala. Deci, momentul de calcul pentru rotile dintate este:

(9)

unde N este numarul satelitilor.

Momentul de calcul pentru imbinarea rotilor planetare cu arbori planetari si pentru arborii planetari este:

(10)

unde l este coeficientul de blocare al diferentialului.

Calculul de dimensionare si verificare al angrenajelor conice din diferential se face dupa metodologia descrisa pentru roti dintate conice cu dantura dreapta.

Calculul axului satelitilor se face sub actiunea fortelor ce actioneaza asupra satelitilor (fig. 18).

Sub actiunea fortei F=2^.F_t (F_t este forta tangentiala din angrenajul satelit-pinion planetar), axul satelitilor este solicitat la forfecare si strivire. Eforturile unitare de forfecare ce iau nastere se calculeaza cu relatia:

(11)

in care: R_m este raza medie de divizare a pinionului planetar; d - diametrul axului.

Eforturile unitare de strivire dintre axul satelitilor si satelit se calculeaza cu relatia:

(12)

Strivirea dintre axul satelitului si carcasa diferentialului se verifica cu relatia:

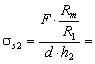
(13)

Datorita solicitarilor la care sunt supuse axele satelitilor, acestea se executa din oteluri aliate cu continut redus de carbon.

In vederea ridicarii rezistentei la uzura, uneori axele satelitilor se aramesc pe toata suprafata cu un strat de 0,01 mm, sau se acopera cu un strat de sulfura de fier.

Pentru evitarea griparii este necesara asigurarea unei ungeri corecte a axelor satelitilor.

Sub actiunea fortelor axiale rezultate din angrenarea satelitului cu rotile planetare, suprafata de contact dintre satelit si carcasa diferentialului este solicitata la strivire. Eforturile unitare de strivire ce apar pe aceasta suprafata se determina cu relatia:

(14)

Calculul asamblarii cu caneluri dintre rotile planetare si arborii planetari se face dupa metodologia prezentata la arborele ambreiajului (cap.1).

4. Transmisiile transversale

4.1. Tipuri constructive de transmisii transversale

Transmisiile transversale sunt unitati functionale independente ce fac legatura intre rotile planetare ale diferentialului si butucii rotilor motoare ale automobilului, cu rolul de a transmite fluxul de putere pentru autopropulsare.

In cazul puntilor motoare spate la care transmisia principala si diferentialul sunt montate de partea nesuspendata a maselor automobilului, cand pozitia relativa dintre rotile motoare si diferential este invariabila, se utilizeaza arbori planetari rigizi.

Cand pozitia relativa dintre rotile motoare si diferential este variabila, se utilizeaza arbori planetari articulati. Structural, arborii planetari au in componenta lor cuplaje unghiulare (C_U), cuplaje axiale (C_A) si cuplaje unghiular-axiale (C_UA). Arborii planetari articulati (fig.19), in functie de tipul mecanismului de ghidare al rotilor, pot forma:

transmisie bimobila (fig. 19, a), obtinuta dintr-un cuplaj unghiular C_U (de obicei homocinetic) ce transmite miscarea de la arborii 1 si 2 ale caror axe formeaza un unghi a, de obicei variabil;

transmisie tetramobila (fig. 19, b), obtinuta prin inserierea a doua cuplaje unghiulare de tipul C_U-C_U si care pot asigura compensari unghiulare si transversale intre arborii de legatura, dar nu si compensare axiala;

transmisie pentamobila sau transmisie universala, obtinuta din inserierea a doua cuplaje unghiulare C_U-C_U cu un cuplaj axial C_A, de tipul C_U-C_A-C_U (fig. 19, c), sau din inserierea unui cuplaj unghiular C_U cu un cuplaj unghiular axial C_UA, de tipul C_U-C_UA (fig. 21, d), facand posibile trei translatii relative (mobilitate axiala si transversala) si doua rotatii relative (mobilitate unghiulara) intre arborii 1 si 2 aflati in rotatie, a caror pozitie este variabila.

4.2. Cuplaje unghiulare

Cuplajele unghiulare ce intra in compunerea transmisiilor transversale sunt cuplaje rigide, homocinetice sau cvasihomocinetice, care, montate intre doi arbori formeaza cu acestia o transmisie bimobila.

a. Cuplaje unghiulare cu elemente articulate. Cel mai simplu cuplaj unghiular utilizat este cuplajul cardanic. Sincronismul miscarii se obtine prin inserierea a doua articulatii cardanice si prin respectarea unor conditii de montare.

Articulatia bicardanica cu cruce, cunoscuta sub numele de cuplaj HOOKE, (fig. 20) se obtine prin scurtarea elementului intermediar. Deoarece furcile exterioare 1 si 2 se pot inclina independent de furca intermediara, nu se asigura sincronismul transmiterii miscarii la unghiuri mari, motiv pentru care sunt fara utilizare actuala. Pentru inlaturarea acestui inconvenient, articulatiile bicardanice cu cruce se prevad, de obicei, cu dispozitive de centrare, care asigura o interdependenta intre cele doua unghiuri prin mentinerea furcii intermediare in planul bisector al furcilor exterioare.

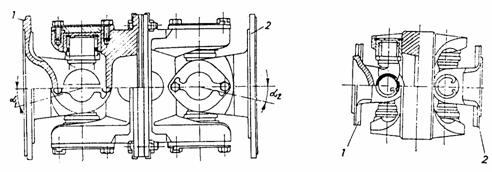
Fig. 20. Cuplaje unghiulare bicardanice fara dispozitiv de centrare

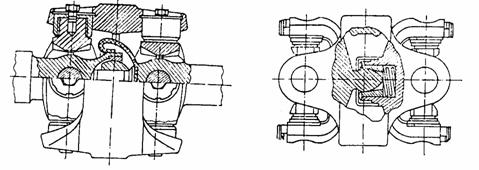
La articulatia bicardanica din figura 21, a, cunoscut sub numele de cuplaj Spicer, dispozitivul de centrare este o cupla tetramobila de tip sfera-cilindru. In cazul articulatiei bicardanice din figura 21, b, cunoscuta sub numele de cuplaj bicardanic homocinetic Borg-Warner, centrarea este asigurata de o cupla tetramobila superioara. Cuplajele unghiulare de acest tip sunt cvasihomocinetice, decalajul unghiular fiind de pana la 7` pentru un unghi de inclinare de 24^o. Aceasta particularitate a permis utilizarea lor atata timp cat vitezele unghiulare si momentele erau modeste.

a)    b)

Fig. 21. Cuplaje unghiulare bicardanice cu dispozitiv de centrare

Cuplajul Tracta (fig. 22) asigura transmiterea sincrona a miscarii de rotatie intre arborii cuplati, legatura dintre elementele cuplajului fiind realizata prin cuple de translatie. Forma si pozitia cuplelor de translatie dintre furcile 1 si 4 ale cuplajului si elementele intermediare 2 si 3 (fig. 22, a) asigura simetria constructiei si deci transmiterea sincrona a miscarii de rotatie. In figura 22, b este reprezentata varianta constructiva a cuplajului Tracta utilizat la automobile.

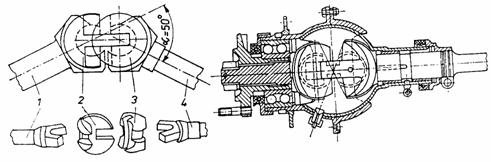
a) b)

Fig. 22. Cuplaj unghiular Tracta

Principalele avantaje ale acestor cuplaje sunt: constructie simpla si compacta; nu necesita conditii deosebite de ungere sau de intretinere; capacitate portanta mare; permit unghiuri mari intre axe (pana la 50^o). Cuplajul necesita o carcasa sferica, etansa, fixa pentru pastrarea mediului de ungere si pentru sustinerea lagarelor arborilor. Se utilizeaza in special la antrenarea rotilor motoare si a rotilor de directie ale autoturismelor cu capacitate marita de trecere, destinate sa lucreze in conditii grele.

b. Cuplajele unghiulare cu elemente de rulare. Au la baza un mecanism spatial desmodrom simetric format din doua elemente, conditia de simetrie fiind asigurata de cupla de centrare dintre elemente, care, pentru imbunatatirea conditiilor de transmitere a miscarii, este realizata cu elemente intermediare de rulare. Cuplajele unghiulare de acest tip mai des intalnite in constructia de automobile sunt cuplajele de tip Weiss si Rzeppa.

Cuplajul unghiular homocinetic Weiss (fig. 23), fabricat de firma Bendix, de unde si denumirea Weiss-Bendix, este format din furcile 1 si 2 ce fac corp comun cu arborele condus si conducator si care sunt prevazute cu canalele A sub forma unor arce de cerc, in care se introduc bilele 3. Bilele, in numar de patru, asigura transmiterea momentului, in fiecare sens, prin jumatate din numarul lor, si inclinarea relativa dintre arborii conducator si condus. Bila 4, montata in locasurile centrale B, serveste la centrarea celor doua furci si la preluarea fortelor axiale din arbori. Fixarea si asigurarea bilei 4 in capatul furcii conducatoare se face prin stifturile 5 si Etansarea cuplajului este asigurata de o carcasa sferica complexa ce sporeste gabaritul radial al acestuia.

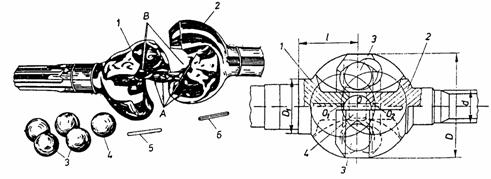
Fig. 23. Cuplaj unghiular Weiss

Cuplajele Rzeppa (fig. 24) asigura transmiterea sincrona a miscarii de rotatie intre arborele conducator 1 si condus 2 prin intermediul corpurilor de rulare 3, mentinute in acelasi plan de colivia 4. Pozitionarea coliviei impreuna cu bilele in planul bisector se face prin realizarea cailor de rulare ale elementului condus pe sfera de raza r, iar a celui conducator pe sfera de raza R, neconcentrice.

Caile de rulare ale aceluiasi element pot fi inclinate toate in acelasi sens, sau in sens opus cele conjugate, sau alternativ in sensuri opuse. Prin inclinarea cailor de rulare in ace1asi sens se realizeaza o mai precisa pozitionare a coliviei in planul bisector, dar fortele axiale, indreptate toate in acelasi sens, ating valori mari. In figura 25 este reprezentata o varianta raspandita a cuplajului Rzeppa, care are cai de rulare orientate in sensuri opuse.

Cuplajele Rzeppa sunt utilizate la turatii de pana la 1500 rot/min si unghiuri de 42.45⁰ intre arbori.

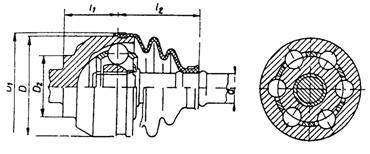
Fig. 2 Cuplaj unghiular Rzeppa cu cai de rulare

orientate in sensuri opuse

4.3. Cuplaje unghiular-axiale

Cuplajele unghiular-axiale ce intra in compunerea transmisiilor transversale sunt cuplaje rigide, homocinetice sau cvasihomocinetice, care, montate intre doi arbori, formeaza cu acestia o transmisie trimobila.

a. Cuplaje Rzeppa. Pornind de la cuplajul unghiular cu colivie autopozitionata (v. fig. 24 si 25), la care caile de rulare ale elementului condus sunt drepte, iar pozitionarea elementelor de rulare in planul de simetrie se realizeaza de catre colivia ghidata sferic in carcasa exterioara a cuplajului, se obtin cuplaje Rzeppa unghiular-axiale. Varianta tehnica a unui cuplaj unghiular-axial Rzeppa este reprezentata in figura 26. Oferta unghiulara este de 22^o iar compensarea axiala poate ajunge pana la 45 mm.

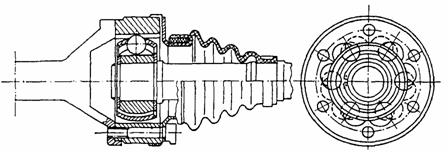
Fig. 28. Cuplaj unghiular-axial Rzeppa

Deplasarea relativa axiala la cuplajele Rzeppa poate fi realizata si prin inserierea unui cuplaj axial cu un cuplaj unghiular. La cuplajul din figura 27, deplasarea axiala se realizeaza prin imbinarea telescopica, cu caneluri, dintre arborele 1 si corpul sferic 2.

b.Cuplaje tripode. La baza cuplajelor tripode simple se gaseste cupla cinematica complexa trimobila, obtinuta prin legarea in paralel a trei cuple pentamobile (fig. 28). Denumirea de "tripod", introdusa de firma Glaenzer Spicer si acceptata, se refera la forma speciala a elementelor cinematice (trei picioare) care permit legarea in paralel a trei cuple cinematice simple. Cuplele pentamobile simple legate in paralel pot fi de tipul cilindru-cilindru (fig. 28,a), sau sfera-plan (fig. 28,b).

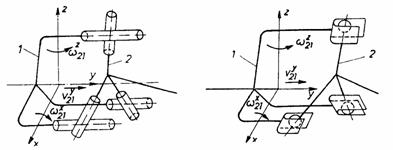
a)    b)

Fig. 28. Cuplaje unghiular-axiale tripode

Se stie ca, in cazul legarii in paralel a cuplelor cinematice, mobilitatea cuplei cinematice complexe rezultate este egala cu suma mobilitatilor comune a tuturor cuplelor componente. In cazul de mai inainte, mobilitatile comune relative sunt si , deci cuplele cinematice tripode sunt unghiular-axiale.

In figura 29 se reprezinta o varianta a cuplajului unghiular-axial tripod cu larga utilizare la autoturismele cu puntea din fata motoare.

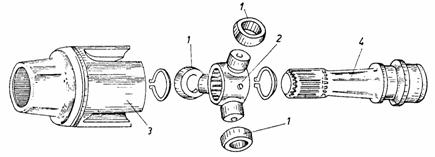
Fig. 29. Elementele constructive ale cuplajului unghiular-axial tripod

La acest cuplaj, miscarea cu alunecare (mai ales in timpul functionarii ca si cuplaj axial) este inlocuita partial prin miscarea de rulare a galetilor sferici 1 in caile de rulare ale elementului 3. Pentru reducerea pierderilor prin frecarea dintre galetii 1 si fusurile elementului tripod 2, la unele constructii se utilizeaza galeti sferici, montati pe ace, sau role.

Elementul tripod 2 este montat prin caneluri pe arborele 4. Raportul de transmitere i pentru cuplajul tripod cu galeti sferici este:

i l ^.sin3j_s

avand valorile extreme:

i_max=1+3^.l; i_min=1 -3^.l, (16)

unde l este un parametru definit de relatia:

, (17)

elementele r, l, a j₃ fiind date in figura 30 (notatiile partilor componente corespund fig. 29).

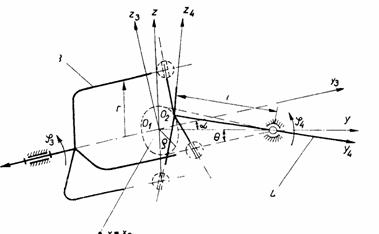
Fig. 30. Elementele cinematice ale cuplajului tripod

Din relatiile 15 si 16 rezulta ca mecanismul tripod cu galeti sferici este teoretic nehomocinetic. Decalajul unghiular maxim (j₄- j₃) si raportul de transmitere pentru valori uzuale ale unghiului a fac ca, practic, mecanismul sa inlocuiasca cu succes cuplajele homocinetice.

Datorita miscarii spatiale a unuia dintre elemente (condus sau conducator), cuplajul tripod nu se foloseste singur, ci inseriat cu un alt cuplaj unghiular. Pentru ca asincronismul sa se reduca si mai mult, este necesar ca arborele ce se interpune intre aceste cuplaje de lungime l (v. fig. 30) sa fie cat mai lung.

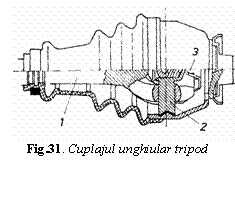
Prin limitarea deplasarii axiale, cuplajul tripod unghiular-axial devine cuplaj unghiular. Constructia unui cuplaj unghiular tripod cu galeti sferici este reprezentata in figura 31. Limitarea axiala se realizeaza prin clema 3 (element elastic), care fixeaza axial elementul tripod 2 de furca condusa l.

4.4. Transmisii universale

Transmisia universala este un lant cinematic pentamobil, destinat transmiterii f1uxului de putere prin miscare de rotatie, intre arborii a caror pozitie relativa este variabila, fiind posibile trei translatii relative (mobilitate axiala si transversala) si doua rotatii relative (mobilitate unghiulara).

Transmisiile universale (fig. 32) se obtin prin inserierea cuplajelor mobile prezentate mai inainte si reprezinta arborii planetari ai puntilor motoare la care exista miscare relativa intre roti si partea centrala a puntii.

Transmisia universala din figura 32, a, este realizata prin inserierea a doua cuplaje unghiulare de tip cardanic 2 si 4 (articulatii cardanice cu cruce) cu un cuplaj axial 3 de tip telescopic. Furca conducatoare a articulatiei 4 se monteaza prin suruburi de o flansa a pinionului planetar al diferentialului, iar furca condusa 1 a articulatiei 2, de butucul rotii.

Transmisia universala Rzeppa (fig. 32,b) se obtine prin inserierea cuplajului unghiular-axial 3 (v. fig. 28) cu cuplajul unghiular 1 (v. fig. 25) prin intermediul arborelui 2.

Transmisia tripoda dubla (fig. 32, c) se obtine prin inserierea cuplajului tripod unghiular-axial cu galetii sferici 1 (v. fig. 29) cu un cuplaj unghiular tripod 3 (v. fig. 31), legate cu arborele 2.

Transmisia universala din figura 32,d rezulta prin inserierea unui cuplaj tripod unghiular-axial 1 cu un cuplaj unghiular Rzeppa 2.

Transmisia din figura 32, e se obtine din inserierea unui cuplaj tripod unghiular-axial 1(v. fig. 29), cu un cuplaj bicardanic centrat 2 (v. fig. 21, a - cuplajul Spicer).

Transmisia din figura 32,f rezulta din inserierea unui cuplaj unghiular Weiss 1 (fig. 23), cu un cuplaj unghiular-axial Rzeppa 2 cu cai de rulare drepte.

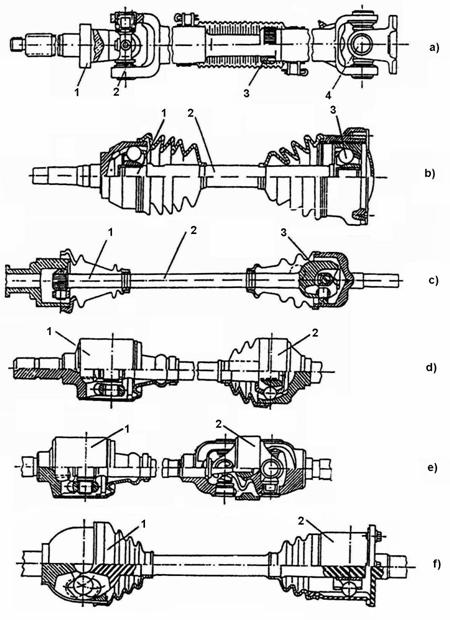
Fig. 32. Tipuri constructive de transmisii universale

Exemplu de calcul

Tema de proiect: Proiectarea mecanismelor de putere ale puntii motoare, pentru un autoturism 4x4, cu urmatorii parametrii initiali:

moment maxim, M_max = 210 Nm.

Z_m = reactiunea normala dinamica la rotile puntii motoare spate,

Z_m = m₂ G₂= 17400 N;

raportul de trausmitere al transmisiei principale, i_o

raportul de transmitere a reductorului, i_R = 1,653

raza de rulare a rotii motoare, r_r = 0,35 m.

a). Calculul transmisiei principale

Angrenajul adoptat pentru transmisia principala a puntii motoare spate pe care trebuie sa o proiectam este de tipul hipoid.

Calculul geometric al angrenajului hipoid

Date initiale:

- numarul de dinti ai pinionului z₁ = 9;

- numarul de dinti ai rotii z₂ = 38;

- raza medie a rotii r_{2 med} = 97 mm;

- deplasarea hipoida    E = 35 mm;

- unghiul conului rotii d

- coeficient de marire pinion k = 1,2.

Determinarea momentului de calcul la pinion

Pentru automobilele cu mai mult de o punte motoare, momentul de calcul se determina prin reducerea la transmisia principala a momentului capabil la roti prin aderenta prin relatia:

Mc₁ = daNm ≈ 900 daNm

Determinarea momentului de calcul la roata condusa

Mc₂ =daNm≈ 3800 daNm

Determinarea elemntelor geometrice ale angrenajului hipoid:

- raportul de transmitere:

i₀ = z₂/z₁ = 38/9 = 4,222

- raza medie a pinionului hipoid

r_1med = k r_{2 med} / i₀ = 1,2 97 / 4,222 = 32,16 mm

- unghiul dintre proiectia normalei comune si axa rotii

tg φ = E / r_{2 med} (tg d + k/i₀) 97(tg70^O+ 1,2/4,222)

se obtine astfel, φ = 6,787^O

- unghiul dintre proiectia normalei comune si axa pinionului

sin e = tg d tg φ = tg70^O tg 6,787 = 0,327

de unde rezulta e =19,08^O

unghiul conului de referinta al pinionului

sin d = cos d cose

sin d = cos70^O cos19,08^O = 0,323 d =18,85^O

- diferenta de inclinare dantura pinion si roata

sin m= sin e/cosd

sin m = sin19,08^O/cos18,85^O = 0,345 m=20,20^O

- unghiul de inclinare a spirei dintelui rotii

tgb = (cos m-1/k)/sinm

tgb = (cos 20,2 ^O-1/1,2)/sin20,2 ^O) b =16,93^O

- unghiul de inclinare a spirei dintelui pinionului

tgb = cosb /k

tgb = cos16,93 /1,2=0,797 b =37,13^O

- lungimea generatoarei medii a conului de referinta al rotii

G_2med = r_{2 med}/sind = 97/sin70^O = 103,22 mm

- lungimea generatoarei medii a conului de referinta al pinionului

G_1med = r_{1 med}/sind = 32,16/sin18,85^O = 99,5 mm

- distanta de la planul cercului de referinta mediu al rotii conduse la planul axei pinionului, masurata pe axa rotii

I₂ = r_{1 med} sind /cosd sin70 ^O /cos18,85 ^O = 31,93 mm

- distanta de la planul cercului de referinta mediu al pinionului la planul axei rotii, masurata pe axa pinionului

I₁ = r_{2 med} cose cos19,08^O = 91,67 mm

- forta tangentiala care actioneaza asupra rotii conduse:

F_t2 = Mc₂ /r_2med = 3800/ 0, 97 ≈ 3900 daN   

- forta tangentiala care actioneaza asupra pinionului

F_t1 = F_t2/k = 3900/1,2 = 3250 daN   

- forta normala pe dinte la roata si la pinion

F_n2 = F_t2 / (cosa_n cosb ) = 3900/cos20 ^O cos16,93^O = 4340 daN

F_n1 = F_t1 / (cosa_n cosb ) = 3250/cos20 ^O cos16,93^O = 3616 daN

- forta axiala pe pinion

F_a1 = F_t1 (tga_n sind + sinb cosd )/cosb =3250(tg20^O sin18,85^O+sin37,13^O cos18,85^O) / cos37,13^O = 2800 daN

- forta axiala pe coroana

F_a2 = F_t2 (tga_n sind - sinb cosd )/cosb

= 3900(tg20 ^O sin70 ^O + sin16,93 ^O cos70 ^O)/cos16,93 ^O = 988 daN

- forta radiala pe coroana

F_r2= F_t2 (tga_n cosd + sinb sind ) / cosb

= 3900(tg20 ^O cos70^O + sin16,93^O sin70^O)/cos16,93^O = 1623 daN

- latimea coroanei dintate a rotii

b₂ = 36 mm

- latimea coroanei dintate a pinionului

b = b₂ sind /(cose cosd Db = 36 sin70 /(cos19,08 cos18,85

= 42,7 mm

- modulul normal in sectiunea medie a dintelui

m_{n med} r_1med. cosb /z₁ = 2 cos27,13/9 =5,7   

- inaltimea piciorului dintelui la roata

b₂ = (f_a + j_r + c_n) m_n 5,7 = 8 mm

- inaltimea capului dintelui la roata

a₂ = (f_a - j_r) m_n 5,7 =1,42 mm

- inaltimea piciorului dintelui la pinion

b₁ = (f_a - j_r + c_n) m_n 5,7 = 2,85 mm

- inaltimea capului dintelui la pinion

a₁ = (f_a + j_r) m_n = (0,7+ 0,45) 5,7 =6,55 mm

- lungimea generatoarei exterioare la roata

G₂ = G_2med b₂ 36 = 121 mm

- lungimea generatoarei exterioare la pinion

G₁ = G_1med + 0,5 b₁ 42,7 = 120,85 mm

- diametrul exterior al rotii

D_e2 = 2(G₂ sin d + h_a2 cosd sin 70 cos70 ) = 228,3 mm

- diametrul exterior al pinionului

D_e1 = 2(G₁ sin d + h_a1 cosd sin 18,85 cos18,85

= 91,9 mm

- grosimea dintelui pe coarda constanta in punctul mediu in sectiune normala roata

S_nc2 = m_n(1,57cos²a_n - x_n sin²a_n) = 5,7(1,57cos²20 sin40

= 6,25 mm

- inaltimea la coarda constanta la dinte roata

h_c2 = a₂ - 0,5 S_nc2 tga_n tg20 = 0,45 mm

- grosimea dintelui pe coarda constanta in punctul mediu in sectiune normala pinion

S_nc1 = m_n(1,57cos²a_n + x_r sin2a_n) = 5,7(1,57cos²20 sin40

= 9,55 mm

- inaltimea la coarda constanta la dinte pinion

h_c1 =a₁ S_nc1 tga_n = 6,55 ^_ 0,5 tg20 = 4,81 mm.

Calculul de rezistenta al angrenajului hipoid

Solicitarile complexe ale angrenajului hipoid fac ca un calcul de rezistenta sa fie in general dificil de realizat exact. Din aceasta cauza se prefera metode mai simple de verificare care pot da o imagine rapida asupra solicitarii.

- puterea transmisa de angrenajul hipoid

N = 0,03 b₂ C_m C_e C_n C₀ kW

unde:

b₂ = 38 mm, latimea danturii;

C_m =1,33 coeficient corespunzator materialului (pentru pinion si coroana executate din oteluri cementate);

C_e coeficientul gradului de acoperire;

C_n = 50 coeficient care depinde de marimea si turatia pinionului;

C₀ = 1

N = 0,03 kW

- calculul efortului de incovoiere la baza dintilor.

MPa

MPa

s_ai = 285 MPa

- calculul solicitarii de contact pe flancul dintilor

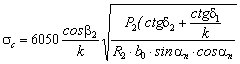
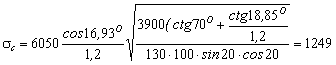MPa

s_c < s_ac = 1870 MPa

Calculul de dimensionare si verificare al arborilor si al lagarelor

Pentru calculul preliminar al arborelui, momentul de calcul se majoreaza cu 1,5 pentru a tine seama si de momentul de incovoiere.

M_ca = Mc

M_ca 1,5 = 1350 Nm.

Diametrul necesar al arborelui va fi in acest caz

mm

Schema de incarcare a arborilor este prezentata in figura 8.2 unde fortele de incarcare axiale, tangentiale si radiale din angrenaj au fost calculate la calculul geometric al angrenajului hipoid (fortele sunt calculate pentru sarcina dinamica maxima

Fortele in angrenaj daN

Folosind metodologia de calcul indicata la calculul lagarelor cutiei de viteze, pentru aceiasi coeficienti de utilizare a treptelor obtinem urmatoarele rezultate:

Fortele in lagare kN

Numarul de cicluri pe care il efectueaza fiecare rulment in fiecare treapta a cutiei de viteze este:

Numarul de cicluri 10⁶ cicluri

Adoptam constructiv urmatoarele tipuri de rulmenti:

Sarcina dinamica echivalenta si durabilitatea rulmentilor adoptati pentru un coeficient de utilizare a momentului motor d = 0,6 sunt urmatoarele:

b).Constructia si calculul diferentialului

Constructia si schema cinematica ale unui diferential simplu, simetric, cu roti dintate conice, sunt reprezentate in figura 33.

Calculul de rezistenta al diferentialelor cuprinde calculul rotilor planetare, calculul satelitilor si al axelor satelitilor.

Pentru calculul organologic este necesar sa se stabileasca pe baza fluxului de putere care circula prin elementele diferentialului momentele de calcul.

- momentul pentru calculul axei satelitilor:

MPa

=950 MPa

- momentul pentru calculul angrenajului pinion planetar-satelit:

=475 MPa

-momentul de calcul pentru arborii planetari:

=1900 MPa

Calculul de dimensionare si verificare al angrenajelor conice

Calculul de dimensionare si verificare al angrenajelor conice din diferential se face dupa metodologia pentru roti dintate cu dantura dreapta:

-momentul de calcul M_c = 475 Nm;

-modulul normal m_n = 3,75;

-numarul de dinti ai satelitului z₁ = 11;

-numarul de dinti ai rotii planetare z₂ = 17;

-unghiul de inclinare al dintelui b = 0^O;

-unghiul de angrenare a =20^O.

- unghiul conului de divizare al satelitului

d = arctg z₁/z₂ = arctg11/17 = 32,9^O;

- unghiul conului de divizare al planetarei

d = arctg z₂/z₁ = arctg17/11 = 57,09^O;

- diametrul de divizare al satelitului

d₁ = m₁ z₁ = 11 = 41,25 mm

- diametrul de divizare al planetarei

d₂= m₂ z₂ = 17 = 63,75 mm

inaltimea capului de divizarea al dintelui

h_{a 1,2} = m_n h₀ 1 = 3,75 mm

inaltimea piciorului de divizare al dintelui

h_{f 1,2} = m_n (h₀+c₀) (1+0,25) = 4,69 mm

- diametrul de cap

d_{a 1,2} = d_1,2 +2 h_{a 1,2} cosd

d_{a 1} cos32,9 = 47,54 mm

d_{a 2}= 63,75+2 cos57,09 = 68,52 mm

- numarul de dinti ai rotii echivalente

z_{1,2 ech} = z_1,2/cosd z_{1 ech} =11/cos 32,9 = 14 dinti

z_{2 ech} = 17/cos 57,6 = 32 dinti.

Calculul axului satelitilor

Calculul axului sateIitilor se face sub actiunea fortelor ce actioneaza asupra satelitilor (figura 34).

Sub actiunea fortei F=2F_t (F_t este forta tangentiala din angrenajul satelit-pinion planetar), axul satelitilor este solicitat la forfecare si strivire.

=2968 daN

Eforturile unitare de forfecare ce iau nastere se calculeaza cu relatia:

= 94 MPa

t_f < t_af = 100 Mpa

Eforturile unitare de strivire dintre axul satelitului si satelit se calculeaza cu relatia :

MPa

s_s1 < s_as1 = 100 MPa

Strivirea dintre axul satelitului si carcasa diferentialului se verifica cu relatia:

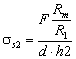
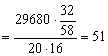MPa

s_s2 < s_as2 = 60 Mpa

c). Calculul arborilor planetari

Transmiterea fluxului de putere al motorului de la diferential la rotile motoare ale automobilului se face prin arborii planetari. Pentru aceasta, arborii planetari sunt solidarizati la rotatie atat cu rotile planetare ale diferentialului cat si cu butucul rotii motoare.

Arborii planetari sunt solicitati la torsiune (de momentul motor transmis de diferential) si incovoiere, functie de modul de montare al butucului rotii.

Deoarece fortele care actioneaza asupra rotii motoare sunt dependente de regimul de deplasare al automobilului, calculul arborilor planetari se face pentru patru regimuri caracteristice de miscare: regimul tractiunii maxime, regimul franarii, regimul deraparii si regimul trecerii peste obstacole.

Schema fortelor si momentele care actioneaza asupra puntii motoare din spate pentru cele patru regimuri este reprezentata in figura 3

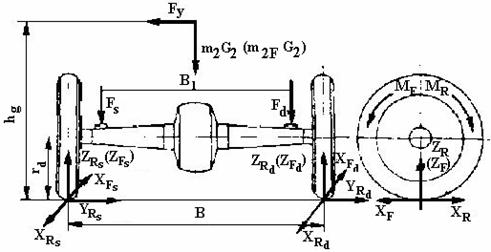
Figura 35

Regimul tractiunii maxime

Regimul tractiunii este caracterizat de actiunea fortei m₂G₂ din partea cadrului sau caroseriei si a fortelor Z_Rs, Z_Rd si X_Rs, X_Rd din partea caii de rulare.

Reactiunile normale Z_Rs si Z_Rd in acest regim, sunt egale si se determina cu relatia :

Z_{R s}= Z_Rd = m₂ G₂/2

in care:

G₂ = 1320 daN - sarcina statica pe cale orizontala la puntea din spate;

m₂ - coeficienrtul de incarcare dinamica a puntii motoare la demaraj.

Pentru automobilele 4x4:

N

unde:

G_a =24 000 N - greutatea automobilului;

a = 1,450 m si b = 1,200 m - coordonatele longitudinale ale centrului de greutate;

L =2,650 m - ampatamentul automobilului;

h_g = 0,65 m - inaltimea centrului de greutate al automabilului;

j = 0,7 - coeficientul de aderenta;

a = 0 - unghiul de inclinare al caii de rulare.

In cazul automobilelor cu mai mult de o punte motoare, cand repartizarea momentului pe punti nu este precis determinata, reactiunile tangentiale se calculeaza pornind de la aderenta rotilor cu calea, folosind reiatia:

X_Rs = X_Rd =Z_Rs j

unde: Z_Rs = Z_Rd - reactiunea normala dinamica

Regimul franarii

Regimul franarii este caracterizat de actiunea fortei m_2FG₂ din par tea cadrului sau caroseriei si a fortelor Z_Fs, Z_Fd si X_Fs, X_Fd din partea caii de rulare.

Reactiunile narmale la frinare sunt egale si se determina din relatia:

Z_Fs=Z_Fd= m_2F G₂/

in care m_2F este coeficientul de incarcare dinamica a puntii din spate la franare; pentru automobile 4x2 si 4x4 cu ambele punti franate.

Reactiunile tangentiale la franare X_Fs, X_Fd se considera egale si limitate la aderenta dintre roti si cale:

X_Fs=X_Fd=Z_Fs j

Regimul deraparii

Regimul deraparii (sau regimul deplasasarii cu reactiuni laterale maxime). In acest caz, asupra puntii actioneaza din partea cadrului sau caroseriei componenta statica a greutatii automobilului ce revine puntii din spate G₂ si componenta fortei laterale F_g, iar din partea caii reactiunile normale Z_Rs, Z_Rd si laterale Y_Rs, Y_Rd.

Din conditia de echilibru a puntii se obtin pentru reactiunile normale expresiile:

Valoarea maxima a reactiunilor laterale este limitata de aderenta rotilor cu calea, deci:

Y_Rs =Z_Rs j si Y_Rd = Z_Rd j

Dar F_y=Y_Rs+Y_Rd=(Z_Rs+Z_Rd) j=G₂ j

Inlocuind expresia fortei se obtin pentru reactiunile normale ale caii expresiile:

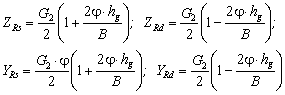
unde: B - ecartamentul puntii.

Regimul trecerii peste obstacole

Regimul trecerii peste obstacole este un regim caracteristic deplasarii pe drumuri cu neregularitati, cand asupra puntii actioneaza sarcini dinamice verticale de valori importante. Marimea acestor sarcini dinamice (care depinde de inaltimea obstacolului, viteza de deplasare, calitatile suspensiei) se apreciaza printr-un coeficient d, definit de relatia :

sau

Valorile reactiunilor pentru cele patru regimuri sunt prezentate in tabelul urmator:

Reactiuni daN

Calculul arborilor planetari

Solutia adoptata pentru arborii planetari este aceea cu arbori planetari total descarcati de momente incovoietoare.

Pentru acest caz de montare, arborii planetari sunt solicitati in regimul tractiunii, la rasucire de momentul :

M_R=X_R r_d = daN m,

unde, d = 32 mm este diametrul arborelui planetar.

Efortul unitar de torsiune este dat de relatia :

MPa;

t_t < t_at