Posibilitati de simulare a sistemelor de reglare automata utilizand programe specifice pentru simularea sistemelor dinamice

1. Scopul lucrarii.

Se prezinta etapele semnificative pentru simularea sistemelor dinamice in SIMULINK, posibilitatile de manipulare a blocurilor si de constructie a modelelor, modul de utilizare a instrumentelor de analiza oferite de SIMULINK. Sunt expuse detalii privind constructia si simularea unor modele simple de sisteme de reglare automata, sunt interpretate raspunsuri indiciale in raport cu comportarea regulatorului si in raport cu parametrii si structura partii fixate.

2. Prezentarea proramului SIMULINK

2.1. Notiuni introductive

SIMULINK este un program pentru simularea sistemelor dinamice. Ca si extensie a programului MATLAB, SIMULINK adauga multe trasaturi specifice sistemelor dinamice pastrand toate functionalitatile generale ale MATLAB-ului.

Dupa instalarea programului SIMULINK directorul MATLAB va contine urmatoarele subdirectoare adaugate, de regula, in subdirectorul TOOLBOXSIMULINK :

SIMULINK - grupul de instrumente sub forma fisierelor cu extensia M ;

BLOKS - grupul de instrumente bloc, blocuri folosind functii S, exemple de mascare, exemple si modele de functii S ;

SIMDEMOS - demonstratii sub forma unor fisiere cu extensia M .

SIMULINK are doua etape succesive de utilizare: definirea sau constructia modelului si analiza acestuia. O sesiune tipica de lucru incepe prin defininirea unui model sau incarcarea unuia definit anterior, dupa care se poate trece la analiza acestuia. In practica acesti doi pasi sunt adesea executati iterativ pe masura ce proiectantul defineste si modifica modelul pentru a obtine comportamentul dorit.

Pentru a usura definirea modelului, SIMULINK adauga o noua clasa de ferestre denumite scheme bloc. In aceste ferestre modelele sunt create si modificate utilizand aproape in totalitate mouse-ul. Performantele obtinute in utilizarea SIMULINK-ului depind in parte de familiarizarea cu metodele de manipulare a componentelor din aceste ferestre.

Dupa ce se defineste un model, acesta poate fi analizat fie prin folosirea optiunilor oferite de meniurile SIMULINK-ului, fie prin introducerea de comenzi in fereastra MATLAB-ului. Instrumentele oferite de program cuprind cateva variante de algoritmi de simulare, linmod, un instrument pentru extragerea modelului liniar al sistemelor, si trim un instrument pentru gasirea punctelor de echilibru.

O simulare poate fi urmarita in timp ce se desfasoara, la sfarsitul acesteia rezultatele finale fiind disponibile in spatiul de lucru al MATLAB-ului.

Pentru simularea sistemelor dinamice in SIMULINK este necesara parcurgerea unor etape prezentate pe scurt in continuare:

1. Se introduce comanda simulink la prompterul MATLAB pentru a deschide biblioteca bloc principala ;

2. Se selecteaza New din meniul File pentru a deschide o fereastra goala, in care se poate construi un model de sistem. Noua fereastra este denumita Untitled si va putea fi redenumita cand se salveaza ca fisier;

3. Se deschid una sau mai multe biblioteci si cu ajutorul mouse-ului se trag blocurile necesare in fereastra activa ;

4. Dupa ce blocurile au fost pozitionate se vor trage linii pentru a le conecta pozitionand cursorul mouse-ului pe portul unui bloc si tinand apasat butonul din stanga al acestuia;

5. Fiecare bloc poate fi deschis prin dublu clic pentru a modifica parametrii interni. Ca parametri pot fi introduse orice expresii permise in MATLAB ;

6. Se salveaza modelul sistemului selectand optiunea Save din meniul File ;

7. Simularea poate fi declansata selectand optiunea Start din meniul Simulation. In timpul simularii optiunea Start se transforma in Stop. Daca se selecteaza Stop meniul va afisa din nou Start ;

8. Parametrii simularii pot fi ajustati selectand optiunea Parameters din meniul Simulation, ceea ce va avea ca rezultat afisarea unei casute de dialog numita Simulation Parameters care permite modificarea lor ;

9. Se poate monitoriza comportarea sistemului modelat folosind un bloc Scope (osciloscop), un bloc Grafic (reprezentare grafica) sau un bloc To Workspace (spre spatiul de lucru) pentru a trimite date in spatiul de lucru MATLAB, unde se pot aplica ulterior functii specifice acestuia asupra rezultatelor simularii.

Ferestrele SIMULINK au fost dimensionate in asa fel incat sa corespunda celor mai des intalnite rezolutii. Totusi, daca monitorul are o rezolutie exceptional de mare sau de mica, dimensiunea ferestrelor s-ar putea sa fie nepotrivita.

Cand se d eschide o biblioteca bloc sau se ruleaza un program demonstrativ pentru prima data, daca dimensiunea implicita nu este corecta, se poate redimensiona fereastra tragand cu mouse-ul de margini. Pot fi apoi salvate noile dimensiuni selectand optiunea Save din meniul File. Data viitoare cand se deschide biblioteca bloc sau se ruleaza programul demonstrativ, fereastra va avea noua dimensiune.

2.2. Posibilitati de constructie a modelelor

Pentru a stapani SIMULINK este necesar sa se cunoasca posibilitatile de manipulare a blocurilor si de constructie a noi modele. Este necesara de asemenea o familiarizare cu tipurile de blocuri disponibile. In sfarsit, trebuie invatat cum se utilizeaza instrumentele de analiza oferite de SIMULINK . Constructia si simularea unui model simplu, descrise in urmatorul capitol, poate constitui o introducere in aceste concepte.

2.2.1. Copierea blocurilor in fereastra de lucru

SIMULINK foloseste reprezentarea sistemelor prin diagrame bloc. Definirea unui sistem este asemanatoare desenarii unei diagrame bloc. Nu se deseneaza insa fiecare bloc individual, ci acestea se pot copia din bibliotecile standard de blocuri furnizate de SIMULINK sau din bibliotecile construite de utilizator. O biblioteca nu este altceva decat un model care include anumite blocuri si subsisteme.

Biblioteca standard de blocuri este organizata in cateva subsisteme, grupand blocurile in functie de comportarea lor. Blocurile pot fi copiate in schema bloc (fereastra de lucru) din aceste subsisteme sau din orice alte biblioteci sau modele. Plasand blocurile care se folosesc cel mai des intr-un astfel de subsistem si setand preferintele personale ca valori implicite, pot fi construite biblioteci personale de blocuri. Acestea vor fi de un real folos in constructia viitoarelor modele.

Biblioteca de blocuri a SIMULINK-ului se deschide tastand comanda: simulink. Aceasta comanda va afisa o fereastra continand iconurile subsistemelor de blocuri care alcatuiesc biblioteca standard (fig. 1.1). Aceste subsisteme pot fi deschise (prin dublu clic) pentru a afisa blocurile pe care le contin si care pot fi copiate in schema bloc.

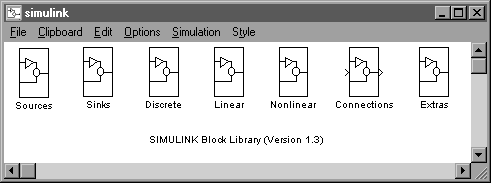
Figura 1.1

Biblioteca Sources, de exemplu, contine blocuri capabile sa genereze semnale. Se poate deschide subsistemul Sources executand un dublu clic pe iconul Sources. Acesta va afisa o noua fereastra continand toate blocurile care produc semnale de iesire dar nu au intrari (fig. 1.2).

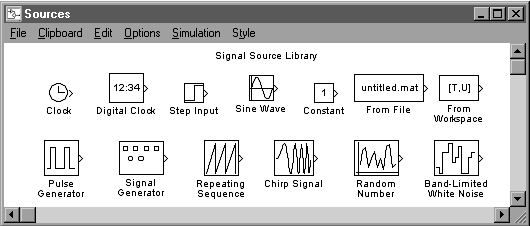
Figura 1.2

Selectand optiunea NewY din meniul File se va deschide o fereastra goala in care se poate incepe constructia modelului. Fereastra se va deschide intr-o pozitie prestabilita, dar poate fi mutata intr-o pozitie mai convenabila, marita sau micsorata.

Blocurile pot fi copiate dintr-o pozitie in alta tragandu-le cu mouse-ul din pozitia originala pana in noua fereastra. Tragand spre exemplu blocul Signal Generator (generator de semnal) din fereastra Sources (surse) in noua, inca nedenumita fereastra, se poate observa ca este deplasata de fapt doar o copie a sa; exista in continuare un bloc Signal Generator in fereastra Sources.

Pentru a observa evolutia semnalului in timpul simularii poate fi folosit blocul Scope. Se deschide biblioteca Sinks si se trage o copie a blocului Scope in fereastra de lucru, in care se vor gasi acum cele doua blocuri (fig. 1.3).

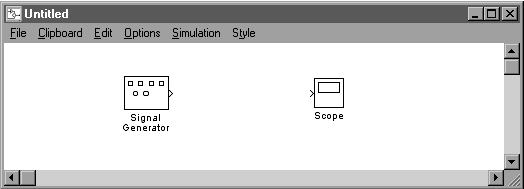
Figura 1.3

Blocurile copiate au parametrii identici cu cei ai blocurilor originale. Majoritatea blocurilor isi expun parametrii in ferestre separate. Aceste ferestre permit controlarea comportamentului blocului prin modificarea valorii parametrilor sai.

Se poate deschide blocul Signal Generator executand un dublu clic pe iconul sau. Aceasta actiune va avea ca rezultat afisarea unei ferestre de dialog continand parametrii de control ai formei de unda, amplitudinii si frecventei generate de bloc (fig. 1.4.).

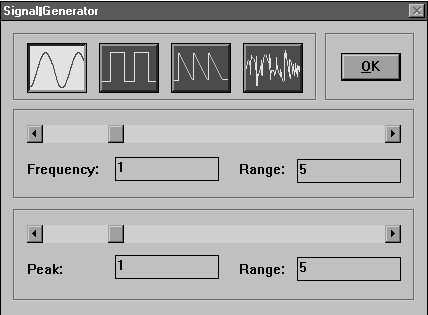
Figura 1.4

Pentru a fixa valoarea frecventei semnalului generat se selecteaza casuta text numita Frequency pozitionand cursorul pe ea si se introduce valoarea dorita. Daca se executa un dublu clic intreaga casuta va fi evidentiata si ceea ce se tasteaza va inlocui valorile anterioare. In aceste cazuri, de introducere explicita a valorii frecventei, variabila Range nu este luata in considerare. Valoarea frecventei poate fi stabilita intre 0 si valoarea introdusa pentru variabila Range prin pozitionarea corespunzatoare a cursorului baretei situata deasupra casutei Frequency. Amplitudinea semnalului generat se stabileste asemanator cu cea pentru frecventa, actionand in casuta Peak. Pentru a inchide aceasta fereastra se executa un clic pe butonul OK sau se tasteaza Enter.

La deschiderea blocului Scope se obtine o fereastra care contine o reprezentare grafica a unui osciloscop. Se plaseaza aceasta fereastra intr-o pozitie convenabila. Folosind cursorul pot fi selectate rubricile corspunzatoare pentru a schimba limitele implicite ale axelor orizontala si verticala introducand noile valori.

2.2.2. Conectarea blocurilor

Semnul ( > ) orientat spre exteriorul iconului blocului Signal Generator reprezinta portul sau de iesire, iar semnul ( < ) orientat spre interiorul iconului blocului Scope reprezinta portul sau de intrare. Pentru a conecta aceste doua blocuri se apsa butonul din stanga al mouse-ului cand cursorul se afla deasupra unui port si se trage o linie de conectare intre cele doua porturi, dupa care se elibereaza butonul.

Cand blocurile sunt conectate corect semnele > , < dispar fiind inlocuite de o sageata care indica sensul deplasarii datelor (fig.1.5.).

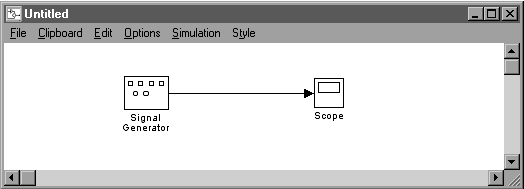
Figura 1.5

Pe masura ce se deseneaza linia ea poate sari in unghiuri care sunt multipli de 45E iar capatul liniei nu va ramane neaparat sub cursor. Linia poate fi desenata sub orice unghi tinand apasate ambele butoane ale mouse-ului (stang si drept in acelasi timp) in timp ce se trage cursorul miscand mouse-ul.

Capatul liniei sare de asemenea pentru a se conecta la orice port de tipul corect ( intrare sau iesire ), daca este tras cursorul destul de aproape de acesta sau deasupra iconului blocului. Daca butoanele mouse-ului sunt eliberate inainte ca blocurile sa fie conectate linia se va termina cu un semn indicand sensul deplasarii datelor ( < sau > ). Pentru a adauga un alt segment se executa un clic pe capatul liniei si se trage in orice directie ; linia va respecta regulile descrise mai sus in ceea ce priveste unghiurile.

In felul acesta pot fi trasate linii de conectare ocolind alte blocuri. Nu exista limite privind numarul sau lungimea liniilor. Pentru a realiza legatura intre generatorul de semnal si osciloscop se procedeaza conform indicatiilor de mai sus. Legatura va determina blocul Scope sa afiseze semnalul generat de blocul Signal Generator. In felul acesta se poate testa daca setarile parametrilor fiecarui bloc in parte au fost corecte.

In cazul in care se considera ca o linie este trasata incorect, linia respectiva se poate sterge sau edita. Se selecteaza linia executand un clic oriunde pe ea. Toate colturile liniei vor fi evidentiate prin mici dreptunghiuri negre numite manere. Odata linia selectata se apasa tasta Delete sau se selecteaza optiunea Cut sau Clear din meniul Edit, pentru a sterge linia din model.

2.2.3. Simularea sistemului

Cand modelul este finalizat, se poate incepe simularea. Pentru a alege metoda de integrare si parametrii care vor fi folositi in timpul simularii, se selecteaza optiunea Parameters din meniul Simulation.

Ca rezultat se va deschide o fereastra, numita Control Panel, care afiseaza toti parametrii simularii care pot fi modificati (fig. 1.6.).

In fereastra sunt afisati parametrii impliciti. Acestia pot fi schimbati acum pentru a putea imbunatati simularea. Selectand casuta text numita Maximum Step Size, se poate schimba valoarea maxima a pasului de integrare, dupa care se executa un clic pe butonul OK pentru a inchide fereastra de dialog. Simularea se decanseaza selectand optiunea Start din meniul Simulation.

Daca fereastra blocului Scope nu este deschisa, se va executa un dublu clic pe bloc; el se va deschide chiar daca simularea a inceput deja. Blocul Signal Generator genereaza functia selectata pentru fiecare pas al timpului iar blocul Scope va afisa graficul acestei functii.

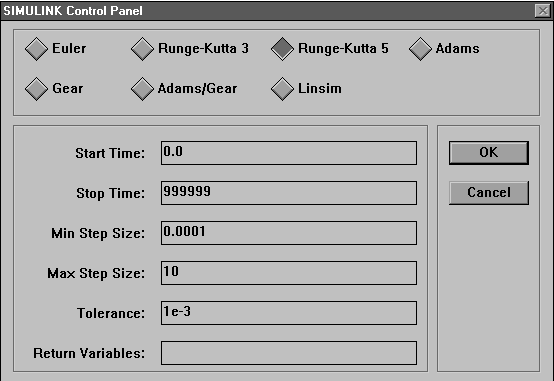
Figura 1.6

Cu valorile implicite ale parametrilor celor doua blocuri, care nu sunt corelate, graficul afisat este cel din figura 1.7.

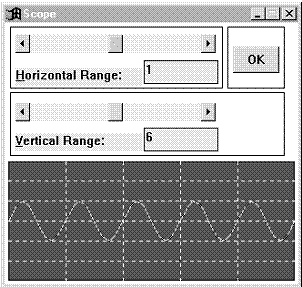
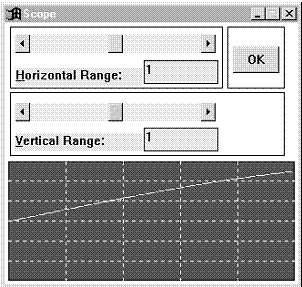
Figura 1.7 Figura 1.8

Pentru a obtine graficul din figura 1.8., se va introduce pentru frecventa generatorului valoarea 2@3.14@5 = 31.4, iar pentru amplitudine valoarea 2 (amplitudinea varf la varf a semnalului va fi 2V). Trebuie remarcat aici ca valoarea introdusa pentru frecventa reprezinta de fapt valoarea pulsatiei (ω = 2πf = 31.4 corespunzatoare unei frecvente f = 5 Hz). Parametrii osciloscopului vor fi setati la valorile: Horizontal Range = 1 ( capatul de scala pe axa timpului 1 sec.) si Vertical Range = 6 ( 1 V / diviziune ).

Parametrii de control ai blocurilor Scope si Signal Generator sunt accesibili in orice moment al simularii. Se poate selecta o forma de unda diferita in blocul Signal Generator si se va observa imediat in fereastra Scope.

Schimband si valorile altor parametrii ai blocurilor Scope si Signal Generator se poate observa modul in care se modifica graficul afisat. Simularea se va opri cand valoarea parametrului Stop Time din fereastra Control Panel este atinsa. Simularea poate fi oprita oricand selectand optiunea Stop din meniul Simulation.

2.2.4. Salvarea modelului

In acest moment exista in fereastra de lucru un model functional care poate fi salvat pe disc ca fisier MATLAB cu extensia M. Un fisier de acest tip contine toate comenzile necesare pentru a descrie modelul astfel incat acesta sa poata fi simulat sau modificat ulterior. Se alege optiunea Save sau Save As din meniul File pentru a afisa o fereastra de dialog in care se poate introduce numele si directorul in care modelul curent va fi salvat.

Se introduce numele modelului, de exemplu model1 si se actioneaza butonul OK pentru a salva modelul in directorul curent. Extensia M va fi adaugata implicit chiar daca nu este introdusa de la tastatura. Se poate schimba directorul in care va fi salvat modelul introducand calea (directorul) in fata numelui fisierului sau executand un clic pe numele directorului dorit si apoi actionand butonul OK. Pentru a selecta un fisier existent, se executa un dublu clic pe numele respectivului fisier sau un clic pe numele fisierului si apoi un clic pe butonul OK. Vor fi vizibile si numele altor fisiere mutand bara de derulare in sus sau in jos.

Dupa ce se salveaza un model intr-un fisier, numele ferestrei in care este afisat modelul va fi identic cu numele fisierului respectiv. Fereastra modelului se poate inchide selectand optiunea Close din meniul File.

Acum exista deja un model salvat pe disc si poate fi deschis acum introducand la prompterul MATLAB comanda :

model1

Modelul va fi afisat intr-o fereastra SIMULINK in aceeasi stare in care era cand a fost salvat. De remarcat ca in acelasi fel am deschis biblioteca de blocuri standard la inceputul sesiunii de lucru anterioare, prin executia din MATLAB a comenzii:

simulink

2.2.5. Manipularea blocurilor in fereastra de lucru

Blocurile pot fi mutate oriunde in fereastra. Chiar daca un bloc este mutat conexiunile acestuia se pastreaza. Daca sunt mutate mai multe blocuri odata isi vor pastra pozitia relativa, liniile de conectare mutandu-se impreuna cu ele. Blocurile Scope, Signal Generator si linia de conectare dintre ele se pot selecta apasand butonul din stanga al mouse-ului cand cursorul se afla deasupra si in stanga obiectelor si tragandu-l pana intr-o pozitie aflata sub si in dreapta obiectelor.

Vor apare mai multe manere in colturile iconurilor blocurilor selectate. Tragand unul dintre blocurile selectate se va observa ca tot grupul se misca simultan cu obiectul selectat.

Pentru a face loc si altor blocuri se muta blocurile in partea de sus a ferestrei. Se aduce apoi o copie a blocului Gain din subsistemul Linear apartinand bibliotecii de blocuri standard.

Se deschide acest bloc executand un dublu clic pe iconul sau. In fereastra de dialog afisata la deschiderea blocului se va schimba valoarea parametrului Gain la 2 si apoi se inchide fereastra. Blocul Gain este un bloc care-si afiseaza valoarea parametrului intern ; valoarea introdusa ca parametru al blocului Gain, in cazul nostru 2, este afisata in interiorul iconului blocului.

Este necesara acum conectarea blocului Signal Generator la blocul Gain. Nici un port de iesire nu este vizibil pe blocul Signal Generator, din moment ce acesta este deja conectat la un bloc, asa ca se va incepe noua linie din punctul in care este conectata linia deja existenta. Se trage cursorul spre blocul Gain conectand linia de acesta. Linia poate fi desenata direct spre portul de intrare al blocului Gain sau poate fi desenata din segmente la diferite unghiuri, de preferinta la unghiuri drepte.

Pentru a muta punctul de intalnire a doua segmente de linie, se executa un clic pe punctul respectiv si se trage cursorul. Cele doua segmente care se intalnesc in acel punct sunt intinse pe masura ce cursorul se misca ; cand butonul mouse-ului este eliberat liniile vor ramane in pozitia la care se afla in acel moment.

Se poate de asemenea muta un segment de linie executand un clic in mijlocul sau si tragandu-l in noua pozitie. Cele doua segmente conectate la capetele segmentului mutat se vor intinde pentru a-si mentine conexiunile. Panta si lungimea segmentului mutat raman aceleasi.

Pentru a introduce un cot suplimentar intr-un segment de dreapta se tin apasate ambele butoane ale mouse-ului tragand cursorul. Segmentul se va frange, punctul de ruptura urmarind cursorul pana cand butoanele vor fi eliberate (fig. 1.9.).

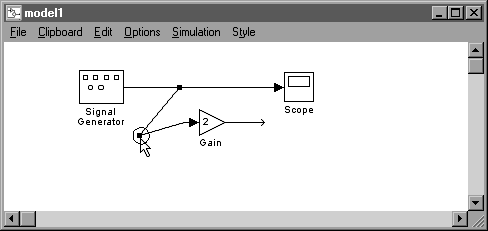
Figura 1.9

2.2.6. Vizualizarea rezultatelor

Odata legat de blocul Signal Generator, blocul Gain va primi in timpul simularii acelasi semnal ca si blocul Scope.

Pentru a adauga un alt bloc Scope in model, nu este necesar sa fie copiat din biblioteca de blocuri. Se poate face o copie a blocului deja existent in sistem tinand apasat butonul din dreapta si tragand blocul intr-o alta pozitie aflata in aceeasi fereastra. Noua copie a blocului Scope va avea aceleasi valori ale parametrilor ca si originalul. SIMULINK-ul adauga automat un numar numelui blocului ( noul bloc se va numi Scope 1 ) atunci cand acesta va fi copiat in aceeasi fereastra. Acest lucru se intampla deoarece numele blocurilor trebuie sa fie unice in interiorul unei ferestre. Se poate, desigur, redenumi un bloc selectand numele acestuia si introducand un nume nou.

Se conecteaza blocul Gain cu noul bloc Scope. Se deschid ambele blocuri Scope si se starteaza simularea. Blocul Gain amplifica semnalul primit de la blocul Signal Generator, in al doilea bloc Scope fiind afisata deci o sinusoida cu amplitudine dubla.

In cazul in care trebuie indepartat un bloc sau o linie dintr-un model se selecteaza obiectul respectiv si apasand tasta Delete sau selectand optiunile Cut sau Clear din meniul Edit, obiectul este sters.

Se selecteaza al doilea bloc Scope ; dupa aceea tinand apasata tasta Shift, se selecteaza linia care il conecteaza cu blocul Gain si linia care conecteaza blocul Signal Generator si primul bloc Scope. Se poate face aceasta executand cate un clic pe fiecare obiect folosind butonul din stanga al mouse-ului. Se indeparteaza obiectele din model selectand optiunea Cut din meniul Edit. Se trage in fereastra modelului un bloc Mux din biblioteca de blocuri Connections.

Se deschide blocul Mux si se schimba valoarea parametrului Number of Inputs la 2, dupa care se inchide fereastra de dialog. Ca rezultat blocul Mux va avea acum doua porturi de intrare. Se conecteaza iesirile blocurilor Signal Generator si Gain la cate unul din aceste porturi de intrare si portul de iesire al blocului Mux la portul de intrare al blocului Scope.

Blocul Mux isi va multiplexa cele doua intrari intr-un singur vector de iesire. Linia de conectare dintre blocurile Scope si Mux este o linie multivariabila care transmite mai multe valori odata.

Se trage acum o copie a blocului To Workspace din biblioteca Sinks in fereastra modelului. Valoarea parametrului Variable Name este afisata in interiorul iconului blocului ; valoarea implicita este yout. Se poatei schimba aceasta valoare introducand un nou nume in casuta text Variable name situata in fereastra de dialog a blocului. Blocul To Workspace ia un vector de orice lungime la intrare si il transmite zonei de lucru MATLAB sub forma unei matrici. Matricea va avea cate o linie pentru fiecare pas al simularii, numarul maxim de linii fiind specificat prin valoarea unuia din parametrii blocului, si cate o coloana pentru fiecare element al vectorului de intrare.

Pentru a schimba numele variabilei MATLAB produse de simulare in ymatr se deschide blocul To Workspace si se introduce noul nume in casuta text Variable name (valoarea implicita maxima a numarului de linii, 1000, este suficienta pentru acest exemplu). Se inchide fereastra de dialog si se va vedea noul nume afisat in iconul blocului (fig. 1.10.).

O alta modalitate de a conecta iesirea uni bloc la intrarea unuia sau mai multor altor blocuri este de a folosi o linie deja existenta. Se pozitioneaza cursorul pe linia care leaga blocurile Mux si Scope, se apasa butonul din dreapta al mouse-ului tragand cursorul spre blocul To Workspace. Se poate observa ca SIMULINK-ul pune un mic cerculet la intersectia celor doua linii pentru a arata ca iesirea blocului Mux va fi transmisa si prin aceasta linie. Se conecteaza linia la blocul To Workspace.

Se starteaza simularea modelului. Se poate observa ca blocul Scope va afisa doua grafice suprapuse datorita faptului ca blocul sau de intrare are doua elemente.

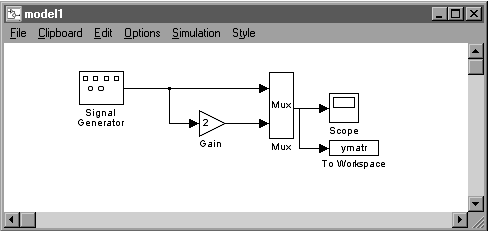
Figura 1.10

La sfarsitul simularii se salveaza modelul selectand optiunea Save din meniul File; versiunea actuala a modelului va fi salvata peste versiunea ramasa de la prima constructie. Pentru a salva modelul curent sub un alt nume se selecteaza optiunea Save As din meniul File si se introduce noul nume.

Daca se selecteaza fereastra de lucru MATLAB si se introduc comanda whos, se va afisa :

Name Size Elements Bytes Density Complex

ymatr 1000 by 2 2000 16000 Full No

Grand total is 2000 elements using 16000 bytes.

Numele variabilei ymatr poate apare afisat impreuna cu alte variabile MATLAB.

Acest exercitiu are rolul de a demonstra ca iesirea oricarui bloc poate fi analizata mai departe folosind intreaga putere a MATLAB-ului. Daca se introduce comanda plot(ymatr) aceasta va avea ca efect afisarea datelor achizitionate in timpul simularii. Graficul va arata ca cel afisat de blocul Scope. Rezultatele simularii pot fi salvate intr-un fisier MATLAB folosind comanda save. Un vector de valori in timp poate fi obtinut conectand un bloc Clock la blocul To Workspace sau introducand un nume de variabila (ex. t ) in campul Return Variables din fereastra Simulation Parameters. Acest vector este necesar deoarece, cu exceptia situatiei in care pasul minim in timp este setat egal cu pasul maxim, simularea se desfasoara in pasi inegali.

2.3. Posibilitati de analiza a modelelor

S-au folosit pana acum uneltele de baza oferite de SIMULINK pentru constructia modelelor. Acest capitol prezinta instrumentele ce permit analiza modelelor SIMULINK. Instrumentele contin functii pentru simulare, liniarizare si determinarea punctului de echilibru (optimizare).

2.3.1. Controlul simularii

Exista trei moduri diferite de a utiliza SIMULINK. Cel mai interactiv mod presupune controlul simularii cu ajutorul meniurilor si urmarirea rezultatelor folosind blocuri Scope sau Graph. Aceasta metoda e usor de folosit si de invatat si poate furniza rapid rezultate. Acest mod de utilizare este deosebit de eficient atunci cand se creaza si verifica un sistem pentru prima data.

Al doilea mod presupune folosirea modelelor predefinite furnizate de SIMULINK si lansarea functiilor de analiza din linia de comanda. Aceasta metoda nu este la fel de interactiva ca prima dar ofera o flexibilitate mai mare. Transmiterea rezultatelor in zona de lucru MATLAB permite analiza si vizualizarea ulterioara a datelor folosind functii grafice specifice acestuia.

Cel mai complex si flexibil mod de utilizare necesita accesul direct al functiilor S ale modelului. Orice model SIMULINK este disponibil in MATLAB sub forma unei functii S care contine comportamentul dinamic al sistemului. Fiecare functie S are un nume identic cu cel al modelului corespunzator. O functie S poate fi apelata in mai multe moduri pentru a furniza informatii despre modelul pe care il reprezinta. Se pot obtine informatii despre numarul de intrari, iesiri si stari ale modelului (continue sau discrete). Se pot obtine deasemenea iesirile si derivatele acestora. Toate instrumentele de analiza furnizate de SIMULINK interactioneaza cu modelele prin intermediul functiilor S. Fisierele de tip M, linmod si trim, sunt exemple care folosesc aceste functii. (Pentru mai multe informatii despre functiile S se poate consulta Gidul utilizator SIMULINK.)

Cele trei moduri de utilizare nu se exclud reciproc si nu se pot delimita exact. Ele pot fi folosite succesiv sau simultan de-a lungul diferitelor etape de dezvoltare a modelului.

Simularea modelelor SIMULINK implica integrarea numerica a unor sisteme de ecuatii diferentiale. SIMULINK furnizeaza o serie de algoritmi de integrare pentru simularea unor astfel de ecuatii. Din pacate, datorita diversitatii comportamentelor dinamice ale unui sistem, nici una dintre aceste metode nu garanteaza simularea eficienta si exacta a oricarui tip de model. Alegerea potrivita a metodei de integrare si setarea cu atentie a parametrilor simularii, sunt conditii necesare pentru obtinerea unor rezultate exacte.

O simulare poate fi pornita fie din linia de comanda, fie din meniul Simulation.

Daca se porneste simularea selectand optiunea Start din meniul Simulation este necesara setarea parametrilor simularii in fereastra de dialog Control Panel care apare selectand optiunea Parameters din meniul Simulation.

Fereastra Control Panel are campuri in care se pot introduce numere sau orice expresii MATLAB corecte, de exemplu, variabilele: tfinal, pasmin, pasmax si err introduse in ordinea campurilor,si care sunt definite in spatiul de lucru MATLAB.

Variabilele [ t, x, y ], introduse la rubrica Return Variables, sunt utilizate pentru transmiterea timpului (intotdeauna), starii (daca exista) si traiectoriilor de iesire (daca sunt utilizate porturi de iesire - biblioteca Sinks) in spatiul de lucru MATLAB. Timpii de start si stop sunt setati in variabilele tstart si respectiv tfinal. Parametrii de integrare err, pasmin si pasmax, controleaza eroarea relativa locala, latimea minima si respectiv latimea maxima a pasului de timp al simularii.

Pornirea unei simulari din meniu permite executarea anumitor operatii interactiv in timpul simularii :

- Schimbarea parametrilor unui bloc, cu conditia ca aceasta sa nu modifice numarul de stari, intrari sau iesiri ale blocului respectiv;

- Schimbarea parametrilor simularii, cu exceptia valorilor introduse la rubricile Return Variables si Start Time.

- Schimbarea algoritmului de integrare.

- Pentru blocurile discrete, schimbarea timpului de esantionare.

- Simularea unui alt sistem in acelasi timp.

- Executand un clic pe o linie de conectare se poate vedea iesirea sa intr-un bloc Scope flotant. Un bloc Scope neconectat se numeste flotant. El va afisa iesirea oricarei linii pe care se executa un clic in timpul simularii.

Adaugarea sau stergerea liniilor sau blocurilor in timpul simularii produce oprirea acesteia. Selectarea optiunii Restart din meniul Simulation va produce reluarea simularii si afisarea rezultatelor modificarilor.

Orice simulare pornita din meniu poate fi pornita si din linia de comanda. De exemplu, pentru a configura o simulare cu aceiasi parametrii ca cei introdusi anterior in fereastra Control Panel, se poate folosi comanda :

[ t, x, y ] = linsim ( Nmodel1N , [ tstart, tfinal ], x0, [ err, pasmin, pasmax ] ) ;

unde model1 este numele diagramei bloc a sistemului.

Comanda linsim('system',tf) integreaza sistemul descris de modelul SIMULINK (sau o alta functie de tip S‑function) >system= de la 0 la TF (timpul final). Fara argumentele din membrul stang rezultatele sunt afisate sub forma grafica. Daca modelul system include porturi de iesire, linsim va reprezenta grafic traiectoriile iesirii in raport cu timpul (altfel sunt reprezentate grafic traiectoriile de stare). Utilizata cu argumentele din membrul stang [ t, x, y ] = linsim('system',tf), comanda linsim returneaza, fara reprezentare grafica, vectorul t ce cuprinde succesiunea momentelor de integrare, traiectoriile iesirilor y si traiectoriile de stare x.

O alta forma a comenzii [ t, x, y ] = linsim('system',tf,xo)', permite definirea conditiilor initiale x0, altele decat cele definite in system.

[ t, x, y ] = linsim('system',tf,xo, options) permite utilizare unor parametrii optionali definiti mai jos:

options(1) - eroarea relativa (default 1e‑3).

options(2) - pasul minim de integrare (default tf/2000).

options(3) - pasul maxim de integrare (default tf/50).

options(4) - neutilizat (default 0).

options(5) - afiseaza parametri de alarma (default 0).

options(6) - valideaza reprezentarea (default -validare daca nu sunt argumentele

grafica a parametrilor din membrul stang, alfel invalidare) (1 validare, 2 invalidare)

Conditiile initiale, care nu pot fi setate in meniu, sunt definite in vectorul x0. Aceste conditii vor inlocui conditiile initiale inscrise in blocuri cu exceptia situatiei in care x0 este o matrice goala.

Pornirea simularii din linia de comanda prezinta urmatoarele avantaje :

- Conditiile initiale din blocuri pot fi suprascrise;

- Daca nu se specifica nici un argument in partea stanga a expresiei, graficele iesirilor vor fi automat afisate sau, cand sistemul nu are iesiri, se vor afisa traiectoriile de stare;

- O simulare poate fi rulata dintr-un fisier de tip M ceea ce permite schimbarea iterativa a parametrilor blocurilor;

- Pentru modele mici, simularea ruleaza ceva mai repede.

Toti algoritmii de integrare au sintaxe de lansare identice asa ca metode diferite pot fi selectate schimband doar numele functiei :

[ t, x, y ] = euler ( NsystemN , tfinal ) ;

[ t, x, y ] = rk23 (NsystemN , tfinal) ;

[ t, x, y ] = rk45 (NsystemN , tfinal) ;

[ t, x, y ] = adams (NsystemN , tfinal) ;

[ t, x, y ] = gear (NsystemN , tfinal).

Performantele simularilor, in termeni de viteza si precizie difera in functie de model si conditii initiale. Sunt prezentate in continuare cateva recomandari privind modul de alegere a metodei de integrare:

linsim - metoda de integrare pentru modele dinamice liniare - se recomanda utilizarea ei in special pentru modele liniare. Aceste modele au de regula in componenta lor blocuri de tipul Transfer Function, State-Space, Zero-Pole-Gain, Sum, si Gain.

Metoda lucreza bine si daca sistemul contine un numar mic de blocuri neliniare. Rezultatele sunt bune, comparate cu alte metode, daca in componenta modelului intra atat blocuri liniare cu dinamica rapida cat si lenta (sisteme dificile).

rk23, rk45 - metode Runge-Kutta de ordinul 3, respectiv de ordinul 5 - asigura rezultate mai bune decat celelalte metode in cazul sistemelor ce contin neliniaritati puternice si discontinuitati. Asigura de asemenea bune performante in simularea sistemelor mixte, ce contin atat blocuri continue cat si discrete. Aceste metode nu dau rezultate satisfacatoare daca in componenta modelului intra atat blocuri cu dinamica rapida cat si lenta. In acest caz se recomanda metodele linsim sau gear.

gear - se utilizeaza in simularea sistemelor neliniare fara discontinuitati. Metoda este destinata simularii sistemelor ce contin atat blocuri cu dinamica rapida cat si lenta. Posibil sa nu lucreze bine pentru sisteme cu singularitati sau daca sistemul este perturbat prin schimbari rapide ale intrarilor.

adams - se utilizeaza in simularea sistemelor neliniare fara discontinuitati si fara constante de timp cu variatii mari.

euler - se utilizeaza numai pentru verificarea rezultatelor obtinute prin celelalte metode.

2.3.2. Vizulalizarea traiectoriilor iesirilor

Traiectoriile iesirilor din SIMULINK pot fi afisate folosind una din metodele urmatoare:

- blocuri Scope sau Graph;

- variabilele returnate si comenzile de afisare MATLAB;

- blocuri To Workspace si comenzile de afisare MATLAB.

Daca se folosesc blocuri Scope sau Graph simularea poate fi pornita din meniu sau din linia de comanda. Afisajul blocului Scope este foarte simplu; nu exista nici o indicatie de scala pe axe, exista doar posibilitatea specificarii capetelor de scala prin variabilele Range. Afisajul blocului Graph gradeaza axele in functie de valorile introduse la setarea parametrilor.

Returnand variabilele in zona de lucru MATLAB se pot folosi comenzile grafice ale acestuia pentru afisarea unor grafice mai explicite.

Blocul etichetat Outport 1 este un port de iesire luat din lista conexiunilor blocurilor (biblioteca Connections) (fig.1.11.).

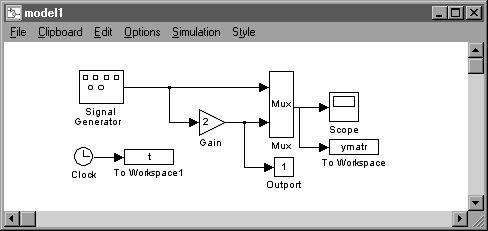
Figura 1.11

Traiectoriile iesirilor se obtin in vectorul de iesire y returnat de functia de integrare ; de exemplu, daca avem un sistem numit model1 comanda :

[ t, x, y ] = linsim ( Nmodel1N , 2 ) ;

va furniza istoria evolutiei in timp a sistemului pan la tfinal=2, care poate fi afisata cu comanda:

plot ( t, y )

Blocul To Workspace poate fi de asemenea folosit pentru a obtine traiectoriile iesirilor. Variabilele sunt disponibile in spatiul de lucru MATLAB dupa ce simularea este completa. Vectorul timp se obtine legand un bloc Clock de un bloc To Workspace (fig. 1.11.). Vectorul timp poate fi obtinut si prin returnarea lui de catre functia de integrare :

t = linsim ( Nmodel1N , 2 ) ;

Se poate observa ca blocul To Workspace poate primi intrari multiple corespunzatoare traiectoriilor stocate ca si vectori coloane ai variabilelor returnate.

2.3.3. Conditii initiale

Conditiile initiale, aplicate sistemului in momentul de timp specificat de valoarea variabilei tstart, sunt in general setate in interiorul blocurilor. Conditiile initiale din interiorul blocurilor pot fi modificate furnizand un vector suplimentar x0 :

[ t, x, y ] = linsim ( Nmodel1N , tfinal , x0) ;

Cand vectorul este vid ( [ ] ) sau nu este specificat, sunt folosite conditiile initiale definite in blocuri; altfel sunt folosite conditiile definite in vectorul x0. (Conditiile initiale nu pot fi modificate daca modelul este simulat din meniu )

Conditiile initiale posibil fixate in blocuri pot fi descoperite folosind comanda :

[ sizes, x0 ] = model1 ;

unde model1 este numele modelului.

Ordinea starilor este disponibila folosind un al treilea argument in partea stanga :

[ sizes, x0, xstr ] = model1;

unde xstr este o variabila sir de caractere care contine in linia i numele blocului si calea asociata starii I.

3. Constructia si analiza unor modele pentru sisteme simple de reglare automata

Se propune in continuare realizarea modelului SIMULINK al unui sistem simplu de reglare automata, corespunzator schemei bloc din fig. 1.12. si simularea raspunsului la un semnal de referinta de tip treapta. Se va considera ca blocul notat Proces reprezinta modelul procesului, considerat aici liniar, model reprezentat prin functia de transfer, si inglobeaza elementul de executie, procesul propriuzis, traductorul si adaptorul de masura. Se va considera de asemenea un regulator continuu de tip PID.

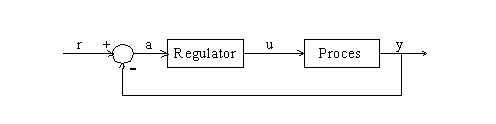
Figura 1.12

Pentru realizarea modelului simulink al acestui sistem se va selecta din nou optiunea New din meniul File si se va deschide o fereastra noua in care se poate incepe constructia modelului. Se salveaza aceasta fereastra intr-un fisier numit model2. In aceasta fereastra se vor copia urmatoarele blocuri:

- generatorul de semnal treapta, blocul Step input din biblioteca Sources;

- sumator de semnale, blocul Sum si modelul procesului, blocul Transfer Fcn din biblioteca Linear;

- regulator PID, blocul PID Controler din biblioteca Extras, grupul de modele intitulat PID Controlers;

- pentru vizualizarea evolutiei iesirii, blocul Graph din biblioteca Sinks.

- pentru a vizualiza si evolutia comenzii, blocul Mux din biblioteca de blocuri Connections.

Denumirile implicite ale blocurilor pot fi redenumite intr-o maniera mai sugestiva. Un bloc se poate redenumi selectand numele acestuia si introducand un nume nou.

Conform celor prezentate la modul de conectare a blocurilor SIMULINK, se vor trasa liniile ce conecteaza blocurile copiate in fereastra de lucru (fig. 1.13.).

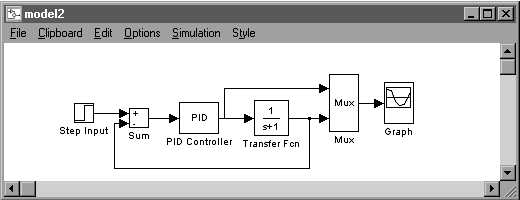
Figura 1.13

Pentru a fixa parametrii semnalului de referinta se deschide blocul Step input si se introduce 0 pentru parametrul Step time, 0 pentru Initial value si 1 pentru Final value. Astfel, acest bloc va genera o treapta unitara (cu salt de la 0 la 1) in momentul declansarii simularii.

Se deschide apoi blocul Sum si se fixeaza semnele cu care intra semnalele in acest bloc, respectiv in ordinea +- (referinta cu + si reactia cu -).

Se va considera un proces simplu, caracterizat printr-o functie de transfer de ordinul I, respectiv:

Pentru a fixa parametrii procesului se deschide blocul Transfer Fcn si se introduce [kp] (vectorul corespunzator coeficientilor numaratorului functiei de transfer) pentru Numerator si [Tp 1] (vectorul corespunzator coeficientilor numitorului functiei de transfer) pentru Denominator.

Se deschide in continuare blocul PID Controler. Se observa ca functia de transfer implementata de acest bloc este de forma:

Pentru termenii proportional, integral si derivativ, respectiv P, I, D se accepta si introducerea unor expresii matematice.

Vor fi luate in considerare modificari de tip treapta ale referintei.

Acordarea regulatorului se va face prin impunerea unui raspuns al sistemului in bucla inchisa (metoda analitica de acordarea regulatorului), respectiv prin impunerea timpului de stabilire T_s sau timpul de raspuns. Comportarea sistemului in bucla inchisa va fi data de :

unde, constanta de timp corespunzatoare sistemului in bucla inchisa, T₀ poate fi calculata in functie de timpul de raspuns: T₀ = T_s / 2.3 daca se considera ca timp de raspuns intervalul de timp dupa care iesirea atinge 90% din valoarea de regim stationar, T₀ = T_c /3 pentru un procent de 95% si respectiv T₀ = T_c /3.9 pentru un procent de 98%. Aceste relatii sunt valabile numai pentru sisteme de ordinul I in care iesirea evolueaza exponential la modificari de tip treapta ale intrarii.

Functia de transfer a sistemului in bucla inchisa data de relatia:

de unde:

A rezultat deci un regulator cu structura PI (D=0). In consecinta, dupa deschiderea blocului PID Controler se introduce pentru parametrul P expresia Tp/(kpT0), pentru parametrul I expresia 1/(kpT0) si 0 pentru parametrul D.

Blocul Graph este folosit pentru vizualizarea evolutiei iesirii procesului. Se deschide si acest bloc si se introduce pentru parametrul Time range valoarea corespunzatoare capatului de scala pentru axa timpului (in cazul nostru 100) , iar pentru parametrii y-min si y-max valoarea

minima si respectiv cea maxima pentru reprezentarea pe ordonata ( valori rezonabile pot fi y‑min=0 si y-max=2). Ultima casuta de text se refera la culoarea reprezentarii grafice respectiv y‑ (yellow) linie continua de culoare galbena pentru primul semnal, g-- (green) linie intrerupta de culoare verde pentru al doilea semnal etc. Nu se modifica parametrii din aceasta rubrica.

In acest moment modelul este finalizat si se poate incepe simularea. Pentru a alege metoda de integrare si parametrii care vor fi folositi in timpul simularii, se selecteaza optiunea Parameters din meniul Simulation. Ca rezultat se va deschide o fereastra Control Panel, afisand valorile implicite ale parametrilor simularii dintre care se va modifica doar parametrul Stop Time pentru care se va introduce valoarea 100. Pasul de integrare se alege automat astfel incat eroarea sa fie mai mica decat valoarea corespunzatoare a parametrului err. Se salveaza din nou modelul.

Se decanseaza simularea selectand optiunea Start din meniul Simulation. Programul afiseaza insa un mesaj de eroare deforma prezentata in fig.1.14.

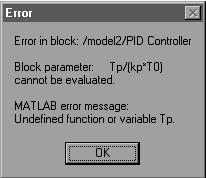
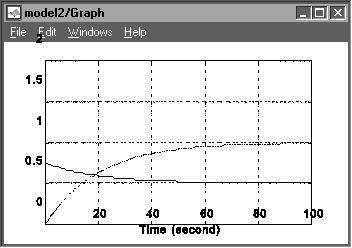
Figura 1.14 Figura 1.15

Pentru a rezolva aceasta problema se trece in fereastra MATLAB si se initializeaza urmatorii parametri:

- kp = 2, Tp= 30, -functia de transfer a procesului;

- T0 = 20, performantele impuse sistemului.

Daca se declanseaza din nou simularea, rezultatele vor fi afisate sub forma graficului prezentat in figura 1.15, unde cu linie continua este reprezentata evolutia comenzii iar cu linie intrerupta cea a iesirii. Se poate observa ca timpul de raspuns al sistemului este de cca 60 secunde. In continuare se pot modifica atat parametrii modelului procesului (kp si Tp), cat si performantele impuse (T0), vizualizandu-se si interpretandu-se rezultatele de fiecare data.

SIMULINK are posibilitatea de a simula si sisteme discrete (sisteme cu esantionare). Modelele pot fi de tip multirate aceasta insemnand ca pot contine blocuri care lucreaza cu perioade de esantionare diferite. Modelele pot fi construite numai din blocuri discrete sau pot fi mixte, continand combinatii de blocuri discrete si continue. Pentru simularea modelelor mixte metodele de integrare Runge-Kutta cu pas variabil sunt superioare celorlalte metode in ceea ce priveste viteza si precizia.

Majoritatea blocurilor discrete sunt incluse in biblioteca de blocuri Discrete. Fiecare dintre aceste blocuri are incorporat un element de esantionare pe intrari si un extrapolator de ordinul zero pe iesiri. Intrarile si iesirile blocurilor discrete sunt actualizate numai la momente de timp ce corespund multiplilor perioadei de esantionare. Perioada de esantionare a unui bloc discret se poate seta in casuta corespunzatoare (Sample Time) din fereastra de dialog afisata la selectia blocului.

Ca o aplicatie imediata a utilizarii blocurilor discrete se va inlocui regulatorul continu PID din modelul precedent printr-un regulator discret. Una dintre posibilitati consta in inlocuirea blocului PID Controller cu blocul Discrete Transfer Fcn din biblioteca de blocuri Discrete. Pentru aceasta se salveaza modelul intr-un nou fisier sub numele model3, se sterge blocul PID Controller si se copiaza blocul Discrete Transfer Fcn. Functia de transfer in s a regulatorului PI utilizat in exemplul precedent este de forma:

Se trece acum in fereastra MATLAB si se discretizeaza functia de transfer continua a regulatorului, cu o perioada de esantionare de 1 sec. (mica in raport cu constantele de timp). Se poate realiza aceasta cu comanda:

[numz,denz]=c2dm([P I], [1 0],1).

Se revine acum in fereastra model3, se selecteaza blocul Discrete Transfer Fcn introduce pentru parametrul Numerator expresia numz, pentru Denominator expresia denz iar pentru Sample time valoarea 1. Rezultatele simularii vor fi identice cu cele obtinute in cazul regulatorului continuu. Se pot face mai multe simulari pentru valori diferite ale perioadei de esantionare. De fiecare data insa, este necesara discretizarea regulatorului continuu pentru valoarea respectiva a perioadei de esantionare, utilizand functia c2dm.

Un model mai eficient se poate realiza utilizand pentru regulatorul discret blocul S‑Domain to Z‑Domain din biblioteca Extras, grupul de blocuri Controllers. Acest bloc are ca parametri de intrare numaratorul si numitorul unei functii de transfer in s si perioada de esantionare. El discretizeaza automat functia de transfer continua corespunzator perioadei de esantionare introdusa si simuleaza modelul discret. Se va incerca aceasta ca tema.

4.Continutul referatului

- prezentarea rezumativa a etapelor semnificative pentru simularea sistemelor dinamice in SIMULINK;

- prezentarea rezumativa a continutului bibliotecilor standard;

- prezentarea sumara a unei metode de acordare a regulatorului, alta decat cea prezentata in lucrare, simularea comportarii sistemului obtinut si interpretarea performantelor de reglare pentru diverse valori ale parametrilor partii fixate.

5. Teme suplimentare

- crearea unei functii S pentru implementarea unui algoritm de reglare sau a unui algoritm de estimare de tipul celor mai mici patrate, asocierea unei diagrame bloc si utilizarea mecanismului de mascare pentru redefinirea ferestrelor de dialog ale acestui bloc.

Bibliografie

[Mat93] *** , SIMULINK, Dynamic System Simulation Software, User=s Guide, The MathWorks Inc., 1993