| CATEGORII DOCUMENTE |
| Aeronautica | Comunicatii | Electronica electricitate | Merceologie | Tehnica mecanica |
Sisteme de reglare automata
1. Proprietati ale sistemelor automate
In cadrul acestui capitol se vor studia trei dintre cele mai importante proprietati, indispensabile asigurarii functionarii sistemelor automate. Prezentarea este orientata pe domeniul sistemelor liniare, conceptele fiind insa generale. Ele se intalnesc si in alte domenii sau pot fi extrapolate si pentru alte domenii.
Pentru ca un sistem sa fie functional se cere ca el sa fie neaparat stabil, adica sa fie capabil sa ajunga intr-un regim de echilibru. Pe de alta parte, este necesar ca un sistem sa poata fi adus in diverse puncte de functionare, iar aceasta operatie sa poata fi efectuata intr-un interval de timp finit. Aceasta a doua cerinta este asigurata prin proprietatea de controlabilitate. In al treilea rand, pentru a asigura diverse strategii de conducere este necesar sa se cunoasca starea sistemului la un moment dat, in particular starea unui sistem condus. Operatia trebuie sa se poata efectua automat pe baza masurarii marimilor de iesireale procesului condus. Proprietatea de a putea asigura aceasta cerinta este numita observabilitate.
Pe de alta parte, datorita faptului ca sunt posibile numeroase regimuri de functionare si datorita faptului ca pentru diverse regimuri parametrii procesului condus variaza in mod notabil, se cere ca proprietatile enumerate (stabilitate, controlabilitate, observabilitate) sa fie robuste. In acest context vorbim despre robustetea sistemelor.
Stabilitatea sistemelor
Conceptul de stabilitate
Evolutia in timp a unui sistem poate fi urmarita in spatiul starilor prin MM-ISI sau prin intermediul marimilor de iesire folosind MM-II. Din punctul de vedere al stabilitatii, in primul caz vorbim despre stabilitate interna, (evidentiata prin marimi de stare), iar in cel de-al doilea caz de stabilitate externa, (evidentiata prin marimi de iesire).
Teorema fundamentala a stabilitatii
Se considera un STC liniar dat prin MM-ISI de forma:
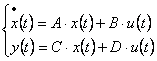 , cu x(0) = 0 (1)
, cu x(0) = 0 (1)
respectiv un STD liniar dat prin MM-ISI de forma:
![]() , cu x(0 = 0. (2)
, cu x(0 = 0. (2)
Se noteaza cu:
![]() (3)
(3)
spectrul matricei A a sistemului (1), respectiv cu:
![]() (4)
(4)
spectrul matricei F a sistemului (2).
Se noteaza cu:
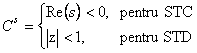 ,
,
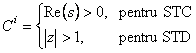 ,
,
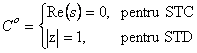 .
.
Teorema fundamentala a stabilitatii se enunta astfel:
Un sistem liniar este asimptotic stabil daca si numai daca spectrul sistemului s(A)ICs.
Un sistem liniar este stabil daca si numai daca spectrul sistemului are componentele in Cs si pe frontiera Co are doar elemente cu ordinul de multiplicitate 1.
Un sistem liniar este instabil daca spectrul
sistemului ![]() si/sau
spectrul sistemului are pe frontiera Co
elemente cu ordinul de multiplicitate mai mare decat 1.
si/sau
spectrul sistemului are pe frontiera Co
elemente cu ordinul de multiplicitate mai mare decat 1.
Teorema fundamentala a stabilitatii se poate aplica numai in cazul sistemelor liniare fara timp mort, caz in care expresiile P(s), respectiv m(z) sunt polinomiale, motiv pentru care se numesc polinoame caracteristice. Polinomul caracteristic se poate obtine pornind de la MM-ISI dupa urmatoarea formula de calcul:
![]() in cazul STC, respectiv:
in cazul STC, respectiv:
![]() in cazul STD.
in cazul STD.
Aplicarea teoremei fundamentale a stabilitatii se mai numeste si criteriul radacinilor, deoarece presupune rezolvarea ecuatiei P(s)=0 (STC), respectiv m(z)=0 (STD) si apoi verificarea conditiilor impuse de teorema. Datorita faptului ca in prezent exista medii de programare care rezolva numeric ecuatii de ordin oricat de mare, aceasta metoda se preteaza la studiul stabilitatii sistemelor liniare de orice ordin.
Metoda a doua a lui Lyapunov
Metoda de analiza a stabilitatii cunoscuta sub acest nume este foarte utila, inclusiv pentru sistemele neliniare.
Primul pas este gasirea unei functii Lyapunov V(x) a unui sistem de forma (1) sau (2), functie care trebuie sa indeplineasca urmatoarele conditii:
V(x) este continua in x si V(0)=0;
V(x) este pozitiv definita;
DV(x) = V(f(x))-V(x) este negativ definita.
In continuare se defineste teorema de stabilitate a lui Lyapunov.
Solutia unui sistem de forma (1) sau (2) este asimptotic stabila daca exista o functie Lyapunov pentru sistem si daca este indeplinita conditia:
![]() ,
,
unde ![]() cand
cand ![]() .
.
Aplicarea teoremei de stabilitate a lui Lyapunov este uneori dificila datorita faptului ca este destul de greu de gasit o functie Lyapunov adecvata. Din acest motiv s-a dezvoltat urmatorul procedeu: daca exista o matrice pozitiv definita P care satisface ecuatia:
![]() , (5)
, (5)
(relatie care poarta numele de ecuatie Lyapunov) unde Q este de asemenea o matrice pozitiv definita, atunci functia Lyapunov poate fi aleasa astfel incat:
![]() (6)
(6)
Astfel determinarea unei functii Lyapunov pentru un sistem liniar se bazeaza pe alegerea unei matrici pozitiv definite Q si rezolvarea apoi a ecuatiei (5). Daca solutia P este pozitiv definita, sistemul este asimptotic stabil.
Metoda locului radacinilor
Aceasta metoda de analiza a stabilitatii sistemelor liniare se bazeaza pe trasarea cu ajutorul unor reguli geometrice a locului radacinilor (LR).
Pornind de la polinomul caracteristic parametrizat in functie de un parametru a al sistemului dat, P(s, a) in cazul STC, respectiv m(z, a) in cazul STD, se poate defini locul radacinilor. Astfel, locul radacinilor este, prin definitie, locul geometric al radacinilor (poli si zero-uri) unui sistem in planul complex "s" (pentru STC), respectiv "z" (pentru STD) cand parametrul a variaza de la zero la infinit.
Ecuatia caracteristica a sistemului este data de relatia:
![]() (7)
(7)
Radacinile ecuatiei (7), dependente de parametrul a vor descrie in planul complex traiectorii care pentru ca sistemul sa fie stabil, trebuie sa indeplineasca conditiile teoremei fundamentale a stabilitatii.
In continuare, LR se va trasa pentru o bucla de reglare cu reactie negativa unitara si cu functia de transfer a sistemului deschis:
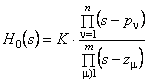 , (8)
, (8)
in cazul STC, respectiv:
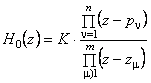 (9)
(9)
in cazul STD. Astfel, desi se utlilizeaza doar polii si zero-urile sistemului deschis, se va trasa in final LR care ne va da informatii despre sistemul inchis.
In continuare se vor prezenta cele noua reguli care ajuta la trasarea LR, pentru sistemele liniare continue. In acest caz, parametrul K poate lua doar valori pozitive.
R1 Locul radacinilor are n ramuri care pornesc din polii sistemului deschis, dintre care m sunt finite si n-m infinite. Ramurile de lungime finita incep in polii sistemului sistemului deschis si se incheie in zero-urile sistemului deschis.
R2 Daca ecuatia caracteristica (7) are coeficienti reali, atunci LR este simetric fata de axa reala.
R3 Toate punctele axei reale care au in dreapta lor un numar impar de puncte critice ale sistemului deschis, apartin locului radacinilor.
R4 Valoarea parametrului K pentru un punct care apartine locului radacinilor de determina cu relatia:
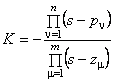 (10)
(10)
R5 Cele n-m ramuri ale LR de lungime infinita tind catre infinit dupa curbe ce admit drept asimptote drepte concurente in acelasi punct pe axa reala, punct numit centru de greutate al configurasiei poli-zero-uri a sistemului deschis si are abscisa data de relatia:
![]() (11)
(11)
R6 Unghiurile formate de asimptote cu axa reala se obtin cu relatia:
![]() , (12)
, (12)
unde x=1,2,., n-m , iar l=0,![]() (n-m)
valori.
(n-m)
valori.
R7 Unghiurile sub care se intersecteaza v ramuri convergente ale LR sunt date de relatia:
![]() , (13)
, (13)
unde v este numarul ramurilor convergente.
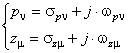
punctele critice ale sistemului deschis, abscisele punctelor de ramificatie ale LR aflate pe axa reala se gasesc printre radacinile ecuatiei:
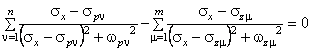 (14)
(14)
R9 Punctele de intersectie cu axa imaginara ale LR se obtin ca solutii ale ecuatiei:
![]() (15)
(15)
In cazul STD, parametrul K poate lua si valori negative. Regulile anterioare se pot aplica la fel ca si in cazul STC, cu urmatoarele exceptii:
R1 LR are n ramuri care incep pentru K ¥, m dintre ele incepand in zero-urile sistemului deschis, iar n-m in punctul de la infinit.Toate se termina pentru K = 0 in polii sistemului deschis.
R3 Toate punctele axei reale care au in dreapta lor un numar par de puncte critice ale sistemului deschi, apartin locului radacinilor.
R6 Unghiurile formate de asimptote cu axa reala se obtin cu relatia:
![]() , (16)
, (16)
unde x iar l=0,![]() (n-m)
valori.
(n-m)
valori.
R9 Punctele de intersectie cu axa imaginara ale LR se obtin ca solutii ale ecuatiei:
![]() (17)
(17)
Locul radacinilor se poate trasa atat folosind metode grafo-analitice bazate pe regulile expuse anterior, fie utilizand metode numerice, utilizand programul MATLAB.
Locul radacinilor este utilizat pentru a aprecia stabilitatea unui sistem atunci cand un parametru variaza intr-un anumit domeniu. Pe baza alurii LR se poate aprecia daca sistemul este sau nu stabil, precum si limitele in care acesta este stabil. De asemenea pe baza LR se pot face aprecieri asupra regimului tranzitoriu al sistemului, fiind utilizat si in proiectarea sistemelor de reglare automata.
Observatie: Locul radacinilor poate fi trasat si pentru alti parametri in afara de coeficientul de amplificare K, cu conditia ca forma functiei de transfer a sistemului deschis sa fie:
![]() , (18)
, (18)
unde cu a s-a notat parametrul, iar cu H' functia de transfer rationala obtinuta ca rezultat al fortarii formei (18). Observatia este velebila si pentru STD, unde variabila s se inlocuieste cu variabila z.
In ceea ce priveste caracterul aperiodic al unui sistem stabil, daca polii acestuia se gasesc in Cs doar pe semiaxa reala negativa a planului "s" sau pe semiaxa reala pozitiva a planului "z", sistemul are un caracter aperiodic.
Atunci cind polii sistemului stabil se gasesc in Cs nefiind in totalitate pe semiaxa reala negativa a planului "s" sau pe semiaxa reala pozitiva a planului "z", sistemul are un caracter oscilant amortizat.
Criterii de stabilitate
Criterii algebrice de analiza a stabilitatii sistemelor liniare
Criteriile algebrice de analiza a stabilitatii sunt de fapt corolarii ale teoremei fundamentale a stabilitatii cu ajutorul carora se poate analiza stabilitatea unui sistem fara a fi nevoiti sa calculam in mod explicit radacinile polinomului caracteristic al sistemului, lucru care uneori poate deveni dificil (d.p.d.v. analitic).
Criteriile de stabilitate algebrice difera in cazul sistemelor liniare continue, fata de sistemele liniare discrete, existind criterii specifice pentru fiecare in parte.
Ø Criterii de stabilitate algebrice pentru STC
Cele mai utilizate criterii de stabilitate algebrice pentru STC sunt criteriile Hurwitz si Routh. Aceste doua criterii sunt de fapt echivalente, difera doar modul de "prezentare".
1. Criteriul Hurwitz
Fie expresia:
![]() , cu an>0 (19)
, cu an>0 (19)
polinomul caracteristic al unui sistem liniar continuu.
Se defineste determinantul de ordinul n:
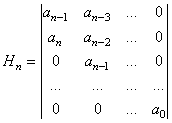 (20)
(20)
care poarta numele de determinant Hurwitz. Fie:
![]() ,
, 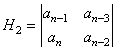 ,
, 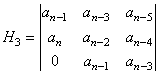 s.a.m.d.
s.a.m.d.
minorii de "N-V" ai determinantului Hurwitz. Criteriul de stabilitate Hurwitz se enunta astfel:
Sistemul de polinom caracteristic (19) este asimptotic stabil daca si numai daca este indeplinita conditia:
![]() (21)
(21)
O conditie necesara, dar nu si suficienta pentru ca un STC sa fie stabil este ca toti coeficientii polinomului caracteristic sa aiba acelasi semn. Din acest motiv, daca aceasta conditie nu este indeplinita, nu se mai aplica nici unul dintre criteriile sau metodele de analiza a STC, fiind evident ca sistemul este instabil.
Daca toti coeficientii acestuia sunt negativi, forma (19) se inmulteste cu -1 si criteriul Hurwitz este aplicat rezultatului astfel obtinut.
Criteriul Hurwitz se utilizeaza de regula pentru analiza stabilitatii sistemelor de ordin redus si pentru determinarea domeniului de stabilitate functie de unul sau mai multi parametri. Acest criteriu nu poate fi aplicat la analiza stabilitatii STC cu timp mort.
Criteriul Routh
Pentru a analiza stabilitatea unui
sistem cu ajutorul criteriului Routh se porneste de la polinomul caracteristic
de forma (19) al sistemului. Cu ajutorul coeficientilor polinomului
caracteristic se construieste un tabel cu (n+1)
linii si ![]() coloane, numit schema lui Routh. Tabelul se construieste astfel:
coloane, numit schema lui Routh. Tabelul se construieste astfel:
pe prima si a doua linie se trec coeficientii polinomului caracteristic, alternativ, in ordinea descrescatoare a puterilor lui s; prima linie incepe cu an, iar a doua cu an-1;
pe prima coloana se trec, incepand cu linia a doua, coeficientii care au expresiile:
![]() , i = 2,.,n (22)
, i = 2,.,n (22)
liniile urmatoare se completeaza cu coeficientii obtinuti conform relatiei:
![]() (23)
(23)
coloana a doua este coloana coeficientilor Routh.
Pentru o mai buna intelegere a modului in care se construieste schema lui Routh, aceasta se ilustreaza in tabelul 1.
|
|
an |
an-2 |
a |
|
|
b |
an-1 |
an-3 |
x |
|
|
b |
r |
r | ||
Tabelul 1
Semnificatia notatiei x din tabelul 1 este urmatoarea:
daca n este par, numarul coeficientilor va fi impar, si pe linia a doua, dupa ultimul coeficient se va completa cu zero;
daca n este impar, numarul coeficientilor va fi par, iar ultimul element din linia a doua va fi a0.
Criteriul lui Routh are urmatorul enunt:
Un sistem liniar continuu este asimptotic stabil daca si numai daca totii coeficientii Routh sunt strict pozitivi.
Criteriul lui Routh se preteaza pentru analiza sistemelor de ordin oricat de mare, fiind in acelasi timp usor de implementat numeric. Nici acest criteriu nu poate fi utilizat la analiza stabilitatii sistemelor cu timp mort.
Ø Criterii de stabilitate algebrice pentru STD
Un criteriu de stabilitate algebric specific sistemelor liniare in timp discret este criteriul lui Jury. Punctul de plecare in analiza stabilitatii STD cu ajutorul acestui criteriu este expresia:
![]() , cu an>0 (24)
, cu an>0 (24)
considerata ca fiind polinomul caracteristic al STD.
Cu ajutorul coeficientilor polinomului (24) se construieste un tabel numit schema lui Jury. Acest tabel se construieste astfel:
prima pereche de linii se completeaza cu coeficientii polinomului caracteristic (24), in prima linie acestia fiind trecuti in ordine crescatoare a puterilor lui z, iar in cea de-a doua linie in ordine inversa;
prima linie din a doua pereche de linii se completeaza cu coeficienti care se calculeaza dua expresia (25), iar a doua linie cu coeficientii calculati anterior, dar in ordine inversa; restul perechilor de linii se vor completa in acest mod, pana la a (n-1)-a pereche de linii;
![]() , k = 1,.,n-1 (25)
, k = 1,.,n-1 (25)
pe prima coloana a tabelului apar coeficientii lui Jury, cate unul pentru fiecare pereche de linii. Coeficientii lui Jury se calculeaza dupa urmatoarea formula:
![]()
Pentru o mai buna intelegere, se ilustreaza prin tabelul 2 modalitea de constructie a tabelului lui Jury.
|
b |
a an |
a an-1 |
an a |
|
|
b |
j j |
j j |
j3n j4n |
|
|
b2(n-1) |
j2n-3,1 j2n-2,1 |
j2n-3,2 j2n-2,2 |
j2n-3,n j2n-2,n |
Tabelul 2
Criteriul lui Jury se enunta astfel:
Un sistem liniar discret este asimptotic stabil daca si numai daca sunt indeplinite urmatoarele conditii:
![]() , (27)
, (27)
![]() , (28)
, (28)
![]()
La fel ca si criteriile algebrice pentru STC, criteriul Jury nu se poate aplica la sisteme cu timp mort. Acest criteriu se preteaza la studiul stabilitatii sistemelor discrete de ordin oricat de mare si la implementarea numerica.
Observatie: In cazul STD, analiza stabilitatii acestora se poate face si in functie de pasul de discretizare h, ca parametru.
Criterii frecventiale de analiza a stabilitatii sistemelor liniare
Criteriile frecventiale de analiza a stabilitatii sistemelor liniare se bazeaza pe studiul sistemelor in domeniul frecventa (pulsatie).
Prezentarea de fata se reduce doar la diferite forme ale criteriului frecvential de stabilitate al lui Nyquist, atat pentru STC, cat si pentru STD.
Ø Criteriul lui Nyquist pentru STC
Criteriul lui Nyquist se aplica pornind de la structura din figura III.1:
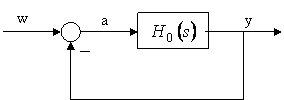
Exista doua variante ale criteriului, in functie de caracteristicile de care face uz pentru analiza stabilitatii, si anume: carecteristicile Bode, respectiv hodograful Nyquist.
In cazul in care se utilizeaza caracteristicile Bode, se defineste notiunea de rezerva de faza:
![]() , (30)
, (30)
unde wt reprezinta pulsatia de taiere a sistemului.
Enuntul criteriului lui Nyquist care se bazeaza pe caracteristicile Bode este urmatorul:
Daca pentru sistemul cu reactie unitara din figura III.1 unde functia de transfer a sistemului deschis H0(s) este de forma:
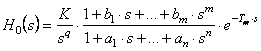 (31)
(31)
unde K>0, qIsi Tm>0, cu polinoamele ![]() si
si ![]() prime intre ele, sistemul inchis este
asimptotic stabil daca si numai daca se indeplineste conditia:
prime intre ele, sistemul inchis este
asimptotic stabil daca si numai daca se indeplineste conditia:
![]() (32)
(32)
Ø Criteriul lui Nyquist pentru STD
Fie sistemul cu reactie unitara din figura III.1, unde variabila s specifica STC se inlocuieste cu variabila z specifica STD. Criteriul de stabilitate Nyquist pentru STD bazat pe carecteristicile Bode se enunta astfel: Un sistem cu structura din figura VII.1 este asimptotic stabil daca este indeplinita conditia:
![]() , (33)
, (33)
unde n este ordinul
sistemului, iar ![]() este
numarul de poli ai sistemului deschis situati in interiorul cercului de raza
unitate sau pe conturul acestuia.
este
numarul de poli ai sistemului deschis situati in interiorul cercului de raza
unitate sau pe conturul acestuia.
Transformarea biliniara
Analiza stabilitatii STD poate fi realizata si cu ajutorul criteriilor specifice STC, utilizand transformarea biliniara data de expresia:
![]() (34)
(34)
sau transformarea biliniara modificata:
![]() (35)
(35)
Formulele de transformare inversa sunt urmatoarele:
![]() (36)
(36)
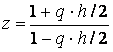 (37)
(37)
In polinomul caracteristic al STD se inlocuieste variabila complexa z cu relatiile (36), (37) de variabila r sau q si asupra polinomului astfel obtinut se aplica apoi criteriile de stabilitate valabile in cazul STC.
Accesibilitatea si controlabilitatea sistemelor
Studiul accesibilitatii, controlabilitatii, cat si a observabilitatii nu difera de la STC la STD. Vom considera un sistem in spatiul starilor dat de relatiile (38), in variabila unificata:
(38)
Prin definitie, starea x0 a unui sistem este controlabila daca exista o comanda care sa conduca sistemul, in timp finit, din starea x0 in starea de repaos.
Pentru studiul controlabilitatii sistemelor liniare s-au dezvoltat unele criterii pornind de la MM-ISI al sistemului, cum sunt criteriile Kalman, respectiv Hautus.
1.2.1. Criteriul Kalman de analiza a controlabilitatii sistemelor liniare
Pornind de la sistemul (38), criteriul Kalman se enunta astfel (atat pentru STC, cat si pentru STD): Sistemul liniar (38) este controlabil daca si numai daca, matricea:
![]() (39)
(39)
numita matrice de controlabilitate are rangul:
rang(Mc) = n , (40)
unde prin n s-a notat ordinul sistemului (38)
1.2.2. Criteriul Hausus de apreciere a controlabilitatii sistemelor liniare
Pornind de la sistemul dat de relatiile (38), criteriul Hausus se enunta astfel: Sistemul (38) este controlabil daca si numai daca, pentru orice lIs(A) este indeplinita conditia:
rang![]() , (41)
, (41)
unde prin n s-a notat ordinul sistemului (38).
Observabilitatea sistemelor
Prin definitie, o stare x0 a unui sistem este neobservabila daca pe baza functiilor u(t) si y(t) cu tI t0, tf nu putem sa determinam starea sistemului la momentul t0, x(t0) = x0.
Un sistem este observabil daca toate starile, in afara de starea de repaos x0 = 0, sunt observabile.
Pentru analiza observabilitatii sistemelor se poate utiliza de asemenea criteriul Kalman.
1.2. Criteriul Kalman de analiza a observabilitatii sistemelor
Pornind de la sistemul dat de relatiile (38), criteriul Kalman de apreciere a observabilitatii sistemelor se enunta astfel: Sistemul dat de (38) este observabil daca si numai daca matricea:
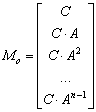 (42)
(42)
numita si matrice de observabilitate, are rangul:
rang(Mo) = n , (43)
unde prin n s-a notat ordinul sistemului (38).
Pentru aprecierea globala atat a controlabilitatii, cat si a
observabilitatii sistemelor, se poate utiliza criteriul lui Gilbert, care se enunta astfel: Fie ![]() functia de transfer a unui sistem S, de
ordinul n, adusa la o forma
ireductibila. Sistemul S este controlabil si observabil daca si numai daca:
functia de transfer a unui sistem S, de
ordinul n, adusa la o forma
ireductibila. Sistemul S este controlabil si observabil daca si numai daca:
grad(N2) = n (44)
Observatie: Daca conditia (44) nu este indeplinita, nu putem sti care dintre proprietati este incalcata. Astfel, suntem obligati sa recurgem la criteriul Kalman pentru a determina care dintre proprietati (controlabilitatea sau observabilitatea), daca nu ambele, lipseste sistemului in cauza.
Cu toate ca atat pentru sistemele in timp continuu, cat si cele in timp discret se trateaza la fel problema controlabilitatii si observabilitatii, o chestiune importanta este alegerea perioadei de esantionare h, astfel incat controlabilitatea si observabilitatea sa nu se piarda prin discretizare. Astfel, daca un STC este controlabil (observabil), conditia ca proprietatea sa se pastreze si in urma discretizarii este:
![]() (45)
(45)
pentru orice poli distincti pa si pb ai STC.
Structuri de reglare
Teoria reglarii este deseori privita ca o ramura a teoriei sistemelor, iar pentru a pune in practica teoria este nevoie de crearea unei legaturi intre lumea reala si teoria abstracta, matematica. Aceasta legatura este de fapt modelarea, proces care prezinta o importanta deosebita.
Teoria reglarii poate fi abordata din diverse directii. Prima metoda sistematica de tratare a problemei legate de reglare dateaza din anii '30 si presupune ca dominante tehnicile bazate pe functii de transfer si cele din domeniul frecventa. Aceasta abordare este considerata clasica. Incepind cu sfirsitul anilor '50 s-a introdus conceptul de variabila de stare si se lucreaza mai mult in domeniul timp. O buna perioada de timp, aceasta abordare a purtat numele de "teoria moderna a reglarii". In prezent se utilizeaza ambele abordari, fiind considerate complementare si egale ca nivel. Cea mai noua abordare este legata de functiile de transfer multivariabile, caz in care sistemele SISO devin un caz particular al acestora.
In fapt, teoria reglarii este de cele mai multe ori legata de aplicatiile fizice. Se considera sistem de reglare orice sistem care exista cu scopul reglarii sau controlului fluxului de energie, informatii, bani sau altor cantitati, de o maniera stabilita. Altfel spus, un sistem de reglare este interconectarea mai multor componente sau unitati functionale asfel incit sa se produca un rezultat dorit.
O prima clasificare a sistemelor de reglare distinge doua categorii de sisteme: sisteme de reglare in circuit deschis (sisteme de conducere figura III.2.a)) si sisteme de reglare in circuit inchis (sisteme de reglare propriu-zise figura III.2.b)).
|
|
|
|
figura III.2
Marimile care intervin au urmatoarea semnificatie:
u = marimea de comanda a procesului tehnic; u este marime de iesire pentru DA si marime de intrare pentru PT, iar din punctul de vedere al sistemului de conducere, este o marime interna. Prin intermediul ei se executa operatia de conducere automata a PT de catre DA.
z = marimea condusa sau iesirea de apreciere a procesului; z este marimea de iesire a sistemului de conducere, valorile si variatiile ei in timp reflectand performantele tehnico-economice realizate de sistemul de conducere si permitand sa se aprecieze satisfacerea dezideratelor tehnologice impuse PT.
y = marimea masurata sau iesirea de masura a procesului; y este o marime interna a SCCI prin intermediul careia se asigura in cadrul SCCI informarea DA cu privire la starea procesului, y este marimea de iesire a unui traductor, marimea masurata de acesta putand fi iesirea de apreciere z sau o alta marime a procesului tehnic. Legatura inversa dintre PT si DA, poarta numele de reactie.
w = marimea de referinta; din punct de vedere functional, w poate fi o marime interna a DA, elaborata de acesta sau o marime externa a DA, prin intermediul careia se prescrie starea dorita a procesului condus sau regimul de functionare al acestuia. Din punct de vedere informational w se considera in ambele cazuri ca marime de intrare a sistemului de conducere.
p = marimea perturbatoare a procesului; p este o marime de intrare pentru PT, modificandu-se independent de DA, p este o marime de intrare si pentru sistemul de conducere u.
Este cunoscut faptul ca sistemul din fig.III.2.b) poate asigura functionarea dorita chiar daca procesul este instabil si in prezenta perturbatiilor (acest efect=compensarea perturbatiilor), pe cand sistemul din fig.III.2a) functionaza doar daca procesul este stabil si/sau perturbatiile sunt cunoscute a priori si bine precizate.
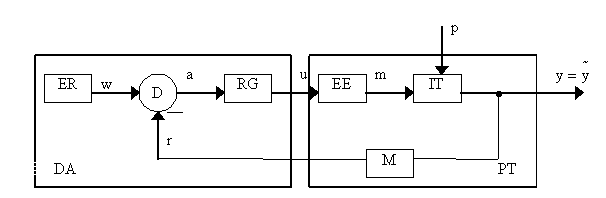 Sistemele de reglare cele mai utilizate sunt sistemele
de reglare dupa eroare, a caror structura este bine cunoscuta. Un SRA
conventional este un sistem de reglare dupa eroare care contine o singura bucla
de reglare (figura III.3).
Sistemele de reglare cele mai utilizate sunt sistemele
de reglare dupa eroare, a caror structura este bine cunoscuta. Un SRA
conventional este un sistem de reglare dupa eroare care contine o singura bucla
de reglare (figura III.3).
Figura III.3
Semnificatia blocurilor este urmatoarea :
ER - element de referinta, care furnizeaza marimea de prescriere w;
D - element de comparare;
RG - regulator;
EE - element de executie
M - blocul de masura;
PT - proces tehnic condus
DA - dispozitivul de automatizare
a - marime de actionare (asimilata cu eroarea de reglare e)s; a=w r, in functie de reactia pozitiva sau negativa existenta;
m - marime de executie, elaborata de EE.
Regulatorul RG elaboreaza marimea de comanda u pe baza algoritmului de reglare:
![]() (46)
(46)
astfel incat ![]() ,
in prezenta perturbatiilor p.
Conditia (46) expliciteaza semnificatia conducerii dupa eroare in sensul
respectarii cat mai fidele de catre marimea reglata y a programului impus prin
marimea de referinta w. Fidelitatea urmaririi de catre marimea y a programului
impus este caracterizata prin performantele uzuale impuse SRA (suprareglaj,
timp tranzitoriu, etc.).
,
in prezenta perturbatiilor p.
Conditia (46) expliciteaza semnificatia conducerii dupa eroare in sensul
respectarii cat mai fidele de catre marimea reglata y a programului impus prin
marimea de referinta w. Fidelitatea urmaririi de catre marimea y a programului
impus este caracterizata prin performantele uzuale impuse SRA (suprareglaj,
timp tranzitoriu, etc.).
Principiul reglarii dupa eroare are prin natura lui o deficienta, si anume pentru ca regulatorul sa poata interveni asupra procesului este absolut necesar sa se produca o eroare, iar interventia asupra acesteia este relativ tardiva. Pornind de la aceasta observatie s-au imaginat o serie de structuri grefate pe cea bazata pe eroare, structuri care imbunatatesc comportarea celei discutate. Avem astfel:
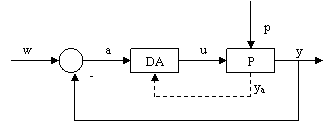
- structura de reglare cu marime masurata auxiliara (fig.III.4.a)),
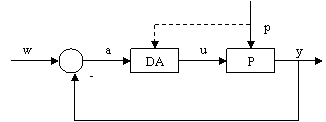
- structura de reglare cu masurarea perturbatiei (fig.III.4.b)),
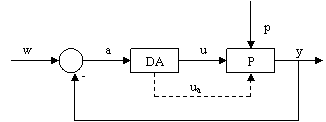
- structura de reglare cu marime de comanda auxiliara (fig.III.4.c)).
Toate cele trei structuri s-au prezentat simplificat.
a)
b)
c)
Figura III.4
a) Structura de reglare cu marime de reactie auxiliara
Cu ya s-a notat marimea de reactie auxiliara, a carei variatie in timp o anticipeaza pe cea a marimii reglate y, permitand dispozitivului de automatizare DA o actiune mai eficienta asupra procesului P si imbunatatind stabilitatea SRA. In categoria SRA cu marime de reactie suplimentara se incadreaza si SRA in cascada. Cascadele de reglare sunt caracterizate printr-un DA special care asociaza fiecarei marimi de reactie o bucla de reglare separata cu un regulator distinct, conectate in serie.
b) Structura de reglare cu compensarea perturbatiei
Aceasta categorie se SRA se utilizeaza in cazul in care marimea perturbatoare p este masurabila. Prin masurarea lui p este posibila interventia mai rapida a DA asupra procesului PT. Dispozitivul de automatizare actioneaza in mare masura pe baza modificarii perturbatiei, neasteptandu-se ca aceasta sa-si manifeste efectul asupra marimii de la iesire.
c) Structura de reglare cu marime de comanda auxiliara
Aceasta categorie de sisteme se utilizeaza in cazul in care procesul este prevazut cu cel putin doua elemente de executie. Prin marimea de comanda principala u este comandat un element de executie, iar prin marimea de comanda auxiliara ua, celalalt element. Marimea ua asigura adaptarea mai rapida a lui y la valoarea prescrisa.
O alta posibilitate de a contracara deficienta sistemelor de reglare dupa eroare consta in realizarea unei reactii dupa stare.
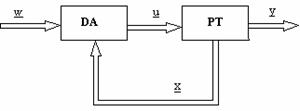
Figura III.5
Marimile care intervin sunt urmatoarele:
u = vectorul marimilor de comanda;
x = vectorul marimilor de stare;
w = vectorul marimilor de intrare;
y = vectorul marimilor de iesire.
Principial, marimea de stare x
contine toate informatiile despre proces. Practic, marimile de stare sunt de
cele mai multe ori nemasurabile in sens direct. In schimb se pot masura
marimile de intrare si de iesire din proces u
si y, si daca procesul este
observabil atunci se poate genera x.
Operatia este realizata de un bloc numit observator
de stare. Marimea furnizata de acesta nu este chiar x, ci doar o estimare a marimii de stare, notata cu ![]() .
.
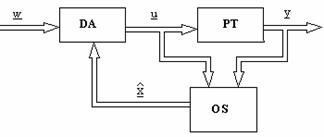
Figura III.6
Sinteza OS este bazata pe urmatorul principiu: OS contine un model al procesului condus a carei iesire se corecteaza in permanenta prin comparare cu procesul real.
Structura de reglare dupa eroare, ca si cea de reglare dupa stare se considera structuri clasice. Progresele tehnicii de calcul si ale electronicii permit procesarea foarte rapida a semnalelor si s-a ajuns astfel la obtinerea unor strategii de reglare performante bazate pe un volum mare de calcul, numite sisteme de reglare avansate (evoluate). Motivul principal al aparitiei unor astfel de structuri il reprezinta neliniaritatile procesului condus existente la marea majoritate a acestora. Aceste neliniaritati pot fi in principiu contracarate doar prin modificarea permanenta a algoritmului de reglare in functie de evolutia punctului de functionare al procesului condus. Structurile capabile de o astfel de implementare se numesc structuri adaptive. In figura III.7. sunt prezentate doua structuri adaptive care implementeaza doua principii de reglare adaptiva.
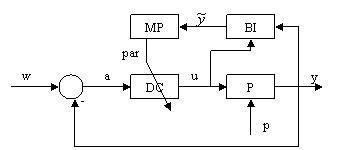
a)
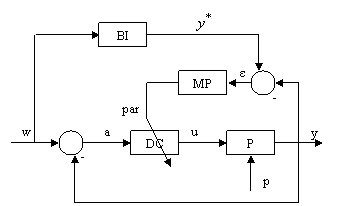
b)
Figura III.7
Algoritmul de reglare este implementat in cadrul dispozitivului de comanda DC si are parametrii par, care se modifica/se adapteaza in cursul functionarii. Schemele din figura III.7. difera prin modalitatea de modificare a parametrilor si avem astfel: structura cu autoadaptare in figura III.7.a). respectiv structura cu model de referinta in figura III.7.b).
Principiul de adaptare in cazul structurii cu autoadaptare este
urmatorul: prin intermediul blocului de identificare BI se identifica procesul
P (de fapt se determina parametrii modelului procesului). Operatia se
efectueaza in functie de u si y iar rezultatul este dat de vectorul ![]() .
In functie de acesta, blocul de modificare a parametrilor MP modifica
parametrii par ai dispozitivului de
comanda.
.
In functie de acesta, blocul de modificare a parametrilor MP modifica
parametrii par ai dispozitivului de
comanda.
In ceea ce priveste cea de a doua structura de adaptare, notiunea de
model de referinta se refera la modul in care iesirea y ar trebui sa se comporte in raport cu marimea de referinta w. Modelul acestei comportari este
implementat prin intermediul blocului ![]() .
In mod ideal, iesirea reala y ar trebui sa se modifice la fel cu
iesirea acestui bloc
.
In mod ideal, iesirea reala y ar trebui sa se modifice la fel cu
iesirea acestui bloc ![]() .
In functie de diferenta dintre cele doua marimi, eroarea
.
In functie de diferenta dintre cele doua marimi, eroarea ![]() blocul de modificare a parametrilor intervine
asupra dispozitivului de comanda.
blocul de modificare a parametrilor intervine
asupra dispozitivului de comanda.
Inafara celor prezentate anterior si care sunt considerate clasice mai exista si alte structuri adaptive bazate pe insasi modificarea algoritmului de reglare ca structura si nu doar ca parametri. Din aceasta categorie se sisteme fac parte sistemele de reglare cu structura variabila, spre exemplu reglajul modal-alunecator.
O alta categorie de sisteme adaptive se obtine prin realizarea dispozitivelor de comanda pe baza de logica fuzzy, retele neuronale sau RIP (Regelbasierte Interpolation). Aceste sisteme fac parte de asemenea si din categoria sistemelor bazate pe cunoastere/sisteme expert.
Un alt concept care intra in categoria sistemelor evoluate este conceptul de conducere optimala. Ideea care sta la baza acestor sisteme este de a genera functia de comanda u astfel incat un anumit indicator de calitate exprimabil cantitativ sa ia o valoare extrema (de regula minimala). Rezultatul aplicarii unui astfel de principiu il constituie generarea marimii de comanda dupa o anumita regula astfel incat u sa poata fi sintetizat din y, u si w. La randul lor, si strategiile de conducere adaptiva pot fi concepute ca strategii optimale prin proiectarea corespunzatoare a mecanismului de adaptare a parametrilor.
Toate structurile prezentate anterior sunt din punct de vedere principial realizabile atat in varianta analogica, cat si in varianta numerica/digitala, caz in care poarta numele de sisteme de reglare numerica . Datorita avantajelor deosebite pe care le ofera tehnica de calcul de ultima ora introdusa in sistemele de reglare, structurile de reglare numerica tind sa preia conducerea in toate domeniile de activitate, prezentand un interes deosebit in ultimii ani si in tara noastra.
In sistemele de reglare numerica, o mare importanta o are procesul de esantionare. Prin definitie esantionarea reprezinta inlocuirea unui
semnal continuu in timp cu o secventa de numere reprezentand valorile
semnalului la momente bine stabilite de timp. Fie Z multimea numerelor
intregi ![]() si
fie
si
fie ![]() o submultime a multimii numerelor reale,
numita multimea momentelor de esantionare. Varianta discretizata/esantionata a
semnalului f este secventa
o submultime a multimii numerelor reale,
numita multimea momentelor de esantionare. Varianta discretizata/esantionata a
semnalului f este secventa ![]() .
Procesul invers, de convertire a unei secvente de numere intr-un semnal
continuu in timp poarta numele de reconstructie
a semnalului.
.
Procesul invers, de convertire a unei secvente de numere intr-un semnal
continuu in timp poarta numele de reconstructie
a semnalului.
Esantionarea este o proprietate fundamentala a sistemelor digitale datorita naturii discrete a calculatoarelor digitale.
O structura de reglare numerica poate fi ilustrata in general astfel:
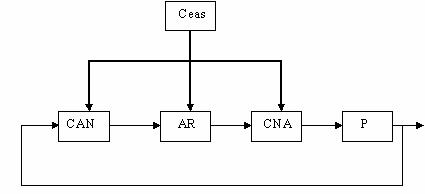
Figura III.8
Variabilele procesului y(t)
sunt esantionate de CAN care le transforma intr-o secventa de numere
care se utilizeaza la elaborarea unei comenzi de asemenea sub forma numerica ,
de catre calculator, prin intermediul unui algoritm de reglare implementat.
Secventa numerica procesata de calculator este apoi convertita de CNA intr-un
semnal continuu in timp u(t), care se
aplica procesului. Toate operatiile sunt controlate de catre ceas. Momentele de
timp la care semnalele masurate sunt convertite in forma digitala se numesc momente de esantionare. Durata,
intervalul de timp dintre doua momente de esantionare succesive se numeste perioada de esantionare, rata de
esantionare sau pas de discretizare
si se noteaza cu h sau Te. Frecventa corespunzatoare![]() (Hz) sau
(Hz) sau ![]() (rad/s) se numeste frecventa/pulsatie de esantionare. In general, momentele de esantionare
sunt egal distantate in timp (periodice), deci
(rad/s) se numeste frecventa/pulsatie de esantionare. In general, momentele de esantionare
sunt egal distantate in timp (periodice), deci ![]() .
.
Daca este cazul, pentru sisteme complexe unde fiecare subsistem component functioneaza la o rata de esantionare prprie, pot fi utilizate si scheme de esantionare mai complicate. De exemplu, se pot folosi perioade de esantionare diferite pentru bucle de reglare diferite. Aceasta strategie poarta numele de esantionare cu rata multipla si poate fi considerata ca o superpozitie a mai multor scheme de esantionare periodice.
Alegerea perioadei de esantionare este critica in sensul ca o perioada de esantionare prea mare poate duce la pierderea de infomatii, semnalul reconstruit fiind altul decat cel esantionat. Ideal ar fi de asemenea ca semnalul continuu sa fie discretizat in mod unic, putandu-i-se asocia doar un singur semnal discret. Pentru esantionare si reconstructie se pot utiliza diverse metode, cum sunt: teorema de esantionare si reconstructie a lui Shannon, elementele de esantionare si retinere (EER) de ordin zero, unu sau mai mare.
Indicatori de calitate ai SRA
1. Indicatori de calitate empirici in domeniul timp
Indicatorii de calitate mentionati se introduc pe baza exemplului unei actionari electrice avand ca marime de intrare turatia prescrisa si momentul de sarcina, iar ca iesire turatia reala. Se efectueaza urmatoarele experimente:
In prima faza consideram ca actionarea se afla in stare de echilibru, marimile mentionate avand valorile n0*, MS0, n0; in continuare se modifica in treapta n0* la valoarea n1*, in timp ce momentul de sarcina MS = MS0 ramane constant. In aceste conditii se va inregistra raspunsul n(t), dat in figura III.9:
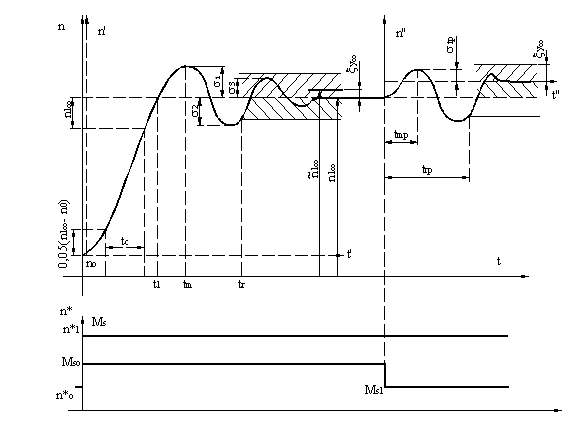
Figura III.9
Pentru aceasta prima situatie, se pot defini urmatorii indicatorii de calitate:
- t1: timpul de prima reglare (sau de prima stabilire) corespunzator intervalului de timp dupa care marimea de iesire atinge pentru prima oara valoarea stationara finala n1¥
- ![]() :
suprareglajul;
:
suprareglajul;
- tr: timpul de reglare, corespunde intervalului de timp dupa care marimea reglata intra in zona de linistire si se pastreaza in aceasta zona; in functie de aplicatie, latimea zonei de linistire este de 2% (n1¥ - n10) sau 5% (n1¥ - n10). Prin zona de linistire se intelege domeniul in interiorul caruia variatiile marimii reglate se considera nesemnificative pentru calitatea procesului de reglare;
- tm: momentul primului extrem;
- tc: timpul de crestere, el se masoara pe frontul raspunsului corespunzator variatiei marimii de iesire de la 5% la 95% din valoarea finala.
Observatie: In cresteri, indicatorii de calitate se definesc fata de sistemul de axe (t'o'n').
Toti indicatorii de calitate mentionati pot
fi masurati experimental. ![]() reprezinta valoarea stationara calculata si in
general
reprezinta valoarea stationara calculata si in
general ![]() ¹ n1¥ Prin definitie:
¹ n1¥ Prin definitie:
ey¥ = n1¥ - ![]() (47)
(47)
reprezinta eroarea de regim stationar a sistemului de reglare. Asemanator cu ey¥ pot apare diferente intre toti indicatorii de calitate masurati si cei calculati. Acest fapt se datoreaza modelarii imperfecte, perturbatiilor necontrolabile si zonelor de insensibilitate ale aparatelor ce compun sistemul de reglare.
2) Pentru cel de-al doilea experiment se pleaca din regimul stationar rezultat in urma experimentului de la punctul 1), modificandu-se in treapta momentul de sarcina MS de la valoarea MS0 la valoarea MS1 in timp ce prescrierea se pastreaza constanta. Se definesc urmatorii indicatori de calitate in raport cu perturbatia:
- trp: timpul de reglare in raport cu perturbatia
- ![]() : suprareglajul care apare la momentul tmp
: suprareglajul care apare la momentul tmp
- tmp: timpul primului extrem in raport cu perturbatia
Similar primului experiment se defineste eroarea de regim stationar in raport cu perturbatia:
eyp¥ = n2¥ - n1¥
Se mai
utilizeaza indicatori cum ar
fi: numarul de oscilatii n respectiv np pana la intrarea in zona de
linistire sau gradul de amortizare: ![]()
![]() sau
sau ![]() .
.
Raspunsurile reprezentate corespund unor procese tranzitorii oscilante; in cazul in care procesele tranzitorii sunt aperiodice nu apar decat o parte din indicatorii definiti.
In proiectare, indicatorilor de calitate empirici li se impun conditii limitative de forma:
![]() <
< ![]() impus tr
< tr impus
impus tr
< tr impus
t1 < t1 impus ![]() p <
p < ![]() p
impus
p
impus
eyp¥ £ eyp¥ impus trp < trp impus u < u impus
Asigurarea simultana a acestor conditii este imposibila. In cazurile practice se vor adopta solutii de compromis, adica se va acorda prioritate unui indicator de calitate sau altuia, dupa caz. Imposibilitatea mentionata se justifica prin caracterul contradictoriu al unor cerinte, cum ar fi:
a) eyp¥ in cazul sistemelor cu statism se datoreaza in primul rand statismului si apoi insensibilitatii aparaturii, reducerea lui eyp¥ in acord cu conditia pusa poate conduce la valori foarte mari pentru KR (coeficient de transfer), respectiv la valori foarte mici ale amortizarii si prin aceasta la o frecventa np mare.
b) reducerea timpului de reglare in mod excesiv inseamna o fortare puternica a procesului, adica punerea in miscare a unor energii relativ mari, controlul acestora fiind dificil si soldandu-se cu suprareglaje mari.
Observatii:
1) Definirea indicatorilor de calitate empirici pe baza raspunsului la semnal treapta se bazeaza pe faptul ca excitarea unui sistem cu un semnal treapta reprezinta o solicitare foarte dura: daca sistemul raspunde corespunzator la o astfel de solicitare, atunci exista garantia unei comportari corespunzatoare si la solicitarile curente.
2) In cazul sistemelor stabilizatoare, intereseaza in principiu indicatorii de calitate determinati de variatia perturbatilor; acestea sunt insa masuri necontrolate de utilizator, astfel incat controlarea unor procese tranzitorii pentru variatii in raport cu semnale treapta nu este de regula posibila; din acest motiv este important raspunsul in raport cu marimea de conducere pe care utilizatorul o stabileste. s si s1p in procente sunt:
![]()
![]()
2. Indicatori de calitate empirici in domeniul frecventa
Pentru definirea indicatorilor de calitate empirici in domeniul frecventa se utilizeaza caracteristicile de frecventa ale S.R.A.
Distingem urmatoarele probleme:
- aprecierea calitatii pe baza c.d.f. ale S.I.
- aprecierea calitatii pe baza c.d.f. ale S.D.
In fiecare caz se pot utiliza caracteristicile logaritmice(caracteristicile reale de frecventa). Se va trata doar cazul aprecierii calitatii S.R.A. pe baza caracteristicilor logaritmice de frecventa ale sistemului inchis (figurile III.10 si III.11).
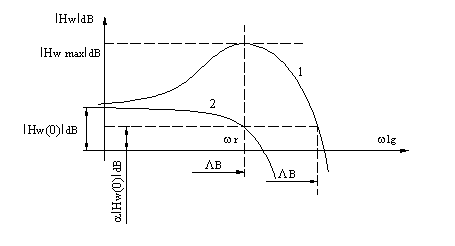
Figura III.10
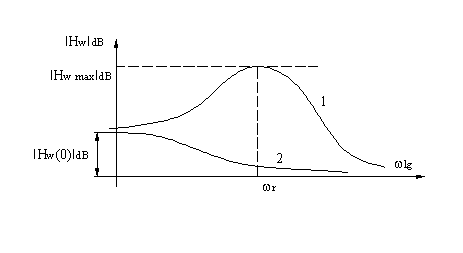
Figura III.11
Traiectoria 1 - corespunde unui sistem oscilant
Traiectoria 2 - corespunde unui sistem aperiodic.
Indicatorii de calitate care pot fi definiti in domeniul frecventa sunt:
wr: pulsatia de rezonanta;
- factorul de rezonanta
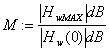
unde Hw(0) corespunde regimului stationar constant
- largimea de banda :
LB
Si in acest caz se pot defini indicatori de calitate asemanatori, in raport cu perturbatia (figura III.12):
wrp : pulsatia de rezonanta;
LBp : largimea de banda
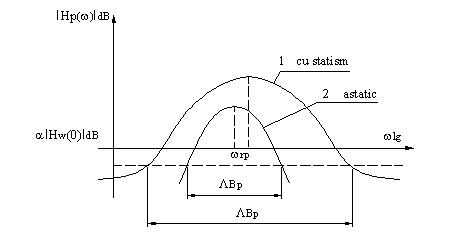
Figura III.12
Traiectoria 1 - corespunde unui SRA cu statism
Traiectoria 2 - corespunde unui SRA astatic
. Indicatori de calitate integrali
Indicatorii de calitate definiti in domeniul timp (empirici) caracterizeaza local comportarea S.R.A., adica la un moment dat sau numai un aspect, respectiv numai un regim; acesti indicatori au avantajul posibilitatii de verificare experimentala.
Atunci cand comportarea locala intereseaza mai putin, fiind important procesul tranzitoriu in ansamblu, se utilizeaza indicatori de calitate integrali.
In cazul S.R.A.c forma acestor indicatori este:
![]()
![]()
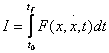 (51)
(51)
Aceasta relatie defineste o functionala pe multimea functiilor x(t) admisibile pentru marimea caracteristica x. Prin functionala intelegem o dependenta care are ca multime de definitie o multime de functii.
Marimea caracteristica x, poate fi marimea reglata y , marimea de actionare a, marimea de c-da c, sau alte marimi care prezinta interes pentru comportarea unui sistem dat dintr-un regim dat.
In functie de problema pe care o rezolva,
respectiv in functie de comportarea sistemului din problema, proiectantul
stabileste care este cea mai adecvata functie F(x,![]() ,t) ce caracterizeaza comportarea
sistemului.
,t) ce caracterizeaza comportarea
sistemului.
Regulatorul trebuie determinat astfel incat I
sa atinga un extrem; in general vorbim despre un minim in ideea ca daca I = 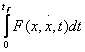 atinge un maxim, atunci
atinge un maxim, atunci
I' = -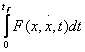 atinge un minim (52)
atinge un minim (52)
O categorie speciala de probleme corespund
cazului cu timp final infinit: tf
= ¥![]() si
si
I
= 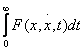 .
(53)
.
(53)
In acest caz, intervalul de integrare fiind
infinit, functia F trebuie sa fie
absolut integrabila, adica 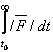 trebuie sa fie finita.
trebuie sa fie finita.
O conditie necesara dar nu si suficienta este
ca ![]() ; in astfel de situatii, avand in vedere
ca F
are termeni in x si
; in astfel de situatii, avand in vedere
ca F
are termeni in x si ![]()
![]() este
necesar ca
este
necesar ca ![]()
![]() si
si
![]() ;
ca urmare, daca pentru procesul studiat se considera o marime caracteristica,
de exemplu y(t), cu ya ¹0, in indicator se
utilizeaza ca marime caracteristica x(t) = y(t) - y¥
;
ca urmare, daca pentru procesul studiat se considera o marime caracteristica,
de exemplu y(t), cu ya ¹0, in indicator se
utilizeaza ca marime caracteristica x(t) = y(t) - y¥
Ca exemple de indicatori de calitate pentru SRAc se pot considera:
1) Indicatori de calitate ai valorilor curente cu pondere temporara:
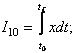
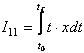 ;
; 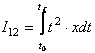 (54)
(54)
2) Indicatori de calitate integrali ai valorilor absolute cu pondere temporara:
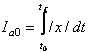 ;
; 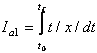 ;
; 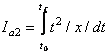 (55)
(55)
3) Indicatori de calitate patratici:
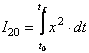 ;
; 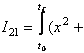
![]() ;
; 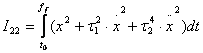 (56)
(56)
Se considera doua S.R.A., pentru care raspunsul la un semnal de intrare dat, are aspectul din figura III.13:
Traiectoria 1- raspuns aperiodic
Traiectoria 2- raspuns oscilant amortizat
valori pozitive si valori negative; in caest caz pot fi utilizati indicatori de forma Iai si I21.
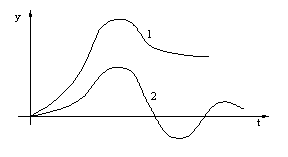
Figura III.13
Pe de alta parte, utilizarea indicatorilor de forma I20 pentru probleme de optimizare, se soldeaza de regula, cu procese puternic oscilante, motiv pentru care se prefera indicatorul I21 care ia in consideratie si derivata lui x; parametrii t sI t au dimensiunea timp si se aleg de proiectant.
Majoritatea dintre indicatorii amintiti au denumiri consacrate. Pentru procese lente este deosebit de utilizat Ia1 cunoscut sub denumirea de indicatorul ITAE.
Alegerea unui indicator de calitate adecvat pentru o problema data, se bazeaza in mare parte pe experienta de proiectare si exploatare.
In cazul sistemelor multivariabile, indicatorii de calitate integrali sunt functionale definite prin relatii de forma
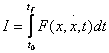 (57)
(57)
unde x este vectorul marimilor caracteristice: vector de stare, vector de c-da, vector care sa reuneasca cele 2 marimi. Foarte des se utilizeaza indicatorul de calitate patratic:
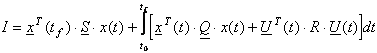 (58)
(58)
unde: x - reprezinta starea sistemului
U - reprezinta comanda
S, Q, R -reprezinta matrici de ponderare alese de proiectant.
Problemele de optimizare se pun astfel: sa se determine u(t) astfel ca I sa fie minim. Indiferent de forma indicatorilor de calitate, rezultatul unei probleme de optimizare este dependent de valoarea initiala x(t0), deci problema minimizarii are si un aspect de incertitudine, deoarece x(t0) este oarecare. Din acest motiv in prezent se urmareste definirea unor indicatori de calitate integrali, care sa nu prezinte acest dezavantaj.
Exista 2 variante:
1) indicatori independenti de x(t0)
2) indicatori pentru care x(t0) se considera ca variabila aleatoare cu o distributie data, astfel incat sa se poata determina un optim absolut.
Indicatorii de calitate patratici prezinta avantajul de a permite dezvoltarea unui numar foarte mare de metode de proiectare a SRA, care pentru un proces dat si pentru un indicator de calitate dat, sa conduca la un regulator pentru care I sa fie minim.
![]()
![]()
![]()
![]()
![]()
![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4854
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved