TENSIUNI SI DEFORMATII ELASTO - PLASTICE IN MEDIILE CU FISURI

1 Modelul analitic al lui Dugdale sI Muskhelishvili

Concentrarea tensiunilor aI deformatiilor in vecinatatea varfurilor fisurilor determina crearea de zone de plasticitate numite enclave plastice. Forma si marimea enclavelor depinde de starea de tensiune de deformatie din varful fisurii. La tensiuni mici de solicitare, enclava se propaga normal pe planul fisurii, avand acelasi aspect pe toata grosimea t a piesei, determinand un mod de deformare de forma unei articulatii plastice, figura 1.

Fig. 1

Pentru tensiuni relativ mari, enclava plastica se extinde tot normal pe planul fisurii, insa planele de alunecare se orienteaza apoi paralel cu planul fisurii, fiind dispuse in doua retele ortogonale intre ele, dar orientate la 45 fata de directia de solicitare, figura 2, iar latimea enclavei plastice este egala cu grosimea piesei. Pentru zone plastice de dimensiuni mici, calculele aferente mecanicii ruperii se bazeaza pe solutia elastica, aproximand fisura reala prin doua fisuri teoretice:

- o fisura mai mare aflata intr-un camp de tensiuni elastice, de semiaxa a₁.

Fig.2

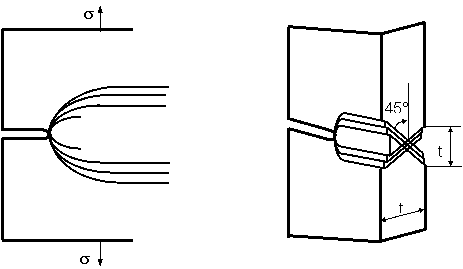
- o fisura practica de semiaxa a.

Fig. 3

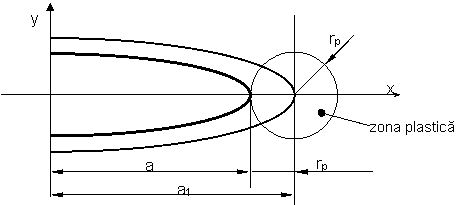
Diferenta dintre cele doua semiaxe se noteaza cu r_p si reprezinta raza zonei plastice, considerata teoretic de forma circulara, figura 3.

Acest model a fost propus de Irwin si imbunatatit de Wells. In acest caz, in intervalul (a, a+2r_p), tensiunile sunt considerate constante si egale cu s_x , iar pentru x > a+2r_p , tensiunile variaza dupa ecuatiile teoriei liniar elastice.

Pentru enclave plastice mai mari trebuie luata in considerare si curgerea extensiva a materialului. Astfel modelul Irwin - Wells a fost perfectionat de Muskhelishvili si Dugdale, purtand numele de model cu fasii de curgere sau benzi de curgere. In cadrul acestui model, formarea si extinderea fisurii satisface urmatoarele conditii :

in zona plastica de la varful fisurii, tensiunea normala ce actioneaza este egala cu limita de curgere a materialului, s_y s_c

enclava plastica de la varful fisurii are forma unei elipse plate;

lungimea zonei plastice satisface conditia ca tensiunea normala de la varful elipsei sa aiba o valoare finita.

a.    Determinarea zonei plastice

O placa infinita aflata intr-o stare de tensiune plana, solicitata monoaxial avand la infinit tensiunea omogena s, contine o fisura strapunsa, centrala, de lungime 2a. Se considera fisura prelungita si-n zona deformata plastic pe lungimea r_p , portiune pe care fisura este solicitata simetric de tensiunile uniforme s_x

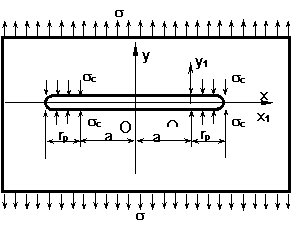
Fig. 4

Materialul din exteriorul enclavei plastice are de asemenea o comportare liniar elastica, motiv pentru care, se poate face analogia sistemului cu o fisura de lungime 2a₁, aflata intr-un camp de tensiuni elastice solicitata de tensiunile s si s_x Situatia mai complexa se defalca in doua aspecte simple:

planul elastic cu fisura de lungime 2a₁, incarcat de sistemul fortelor exterioare s caruia ii corespunde factorul de intensitate a tensiunii K_e ,

unde:

; (1)

planul elastic cu fisura 2a₁ incarcat pe intervalul simetric (a,a+r_p) cu sistemul echilibrat de tensiuni uniforme s_x, incarcare careia ii corespunde factorul de intensitate a tensiunii K_p, care se determina pornind de la metoda transformarii integrale:

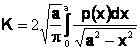(2)

pentru situatia de mai sus: a a+r_p ; p(x)=s_c, iar:

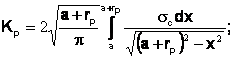(3)

Se face schimbarea de variabila (a+r_p) sin t = x si dx = (a+r_p)cos t dt , iar

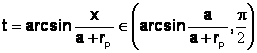
Deci:

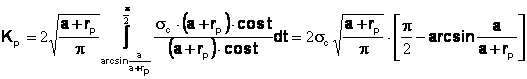, adica:

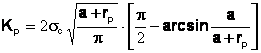(4)

intinderea zonei plastice rezulta din conditia ca tensiunea sa fie marginita la capatul zonei plastice (a+r_p), conditie realizata numai daca : K_e - K_p = 0.

inlocuind expresiile celor doi factori de intensitate a tensiunii, rezulta:

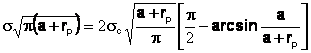, respectiv:

si aplicand functia cos se obtine:

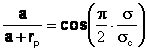
de unde:

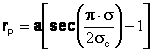(5)

Dezvoltand in serie, rezulta:

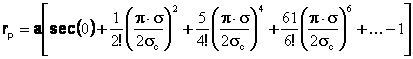(6)

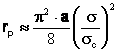(7)

Dar , de unde:

(8)

expresie valabila numai daca r_p<< a si s << s_c

b.Expresia functiei lui Westergaard

Fie o placa infinita cu o fisura centrala de lungime 2a₁ , inclusiv enclava plastica, solicitata atat de tensiunea exterioara s , figura 5 a, de sarcina concentrata S pe fisura, figura 5 b, respectiv de sarcina uniform distribuita s, figura 5 c.

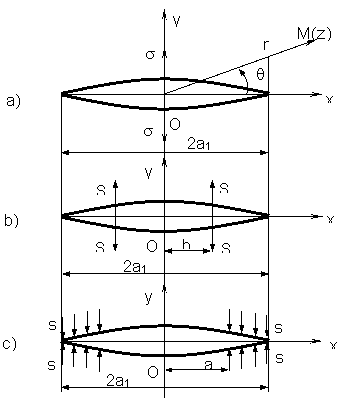
Fig. 5

Pentru cazul (a) campul de tensiuni si de deformatii este pus in evidenta de functia lui Westergaard

(9)

Pentru cazul (b) revenind la expresia functiei

(10)

iar Z*=2j(z) si punand conditiile la limita pentru incarcarea data in cazul (b), rezulta:

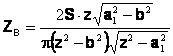(11)

Pentru cazul general, figura 5 c, cand fisura este solicitata atat de tensiunile uniform distribuite s , cat si de sarcinile uniform distribuite pe fisura s , pe lungimea a₁ - a, functia lui Westergaard se va calcula cu relatia:

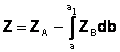(12)

Introducand expresiile pentru Z_A , Z_B , calculand integrala si efectuand notatia : , se obtine:

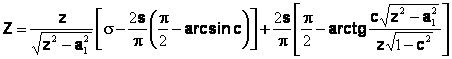(13)

Punand conditia : , primul termen se anuleaza, iar functia Z devine:

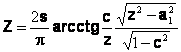(14)

c. Concluzii

Modelul analitic propus de Dugdale, figura 6, este reprezentat printr-o fisura aflata intr-un camp de tensiuni elastice, de lungime 2a asupra careia actioneaza tensiunea la infinit s. Aceasta se extinde de la valoarea 2a la valoarea 2a₁. Deplasarile suprafetelor fisurii sunt impiedicate de tensiunile interne distribuite, notate cu s, care pe unitatea de suprafata de rupere sunt egale cu limita de curgere a materialului s_c

Fig. 6

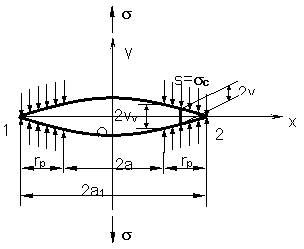
Tensiunile care inconjoara varful fisurii sunt asemanatoare cu niste rezemari locale, in zona plastica, de forma unor articulatii plastice. Fisura de lungime 2a₁ solicitata simultan de tensiunile s si s_c corespunde unei fisuri reale de lungime 2a , avand zonele plastice de forma unor pene din material in stare de curgere si au la baza grosimea 2v_v, respectiv in interiorul zonei plastice o grosime curenta 2v, figura 7. Presupunerea ca sarcina distribuita s este constanta si egala cu limita de curgere s_c este valabila numai pentru metale, unde deplasarea v_v este mica, iar cresterile deformatiei specifice sunt neglijabile.    Pentru piese cu variatii mai mari de grosime, unde deformatia plastica are loc la volum constant sau la materiale care prezinta o intarire plastica insemnata (ecruisare), tensiunile s nu mai sunt constante, variind in limite largi, astfel modelul lui Dugdale si Muskhelishvili se foloseste cu anumite corectii aduse.

Fig. 7

2 Tensiuni si deplasari in zona elasto - plastica de la varful fisurii

Tensiunile si deplasarile anumitor puncte din vecinatatea varfului fisurii se determina utilizand expresia functiei lui Westergaard :

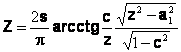(15)

care inlocuita in expresiile tensiunilor din aproximarea lui Irwin:

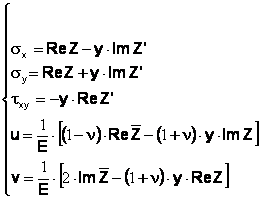(16)

pentru primul mod de propagare a fisurii, sau:   

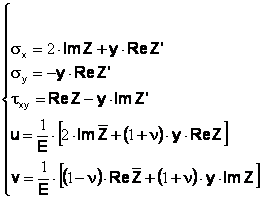(17)

pentru modul al doilea de propagare a fisurii.

Pentru un punct situat pe axa Ox, la distanta x>a₁ , tensiunea normala, s_y , perpendiculara pe directia de propagare a fisurii va avea expresia:

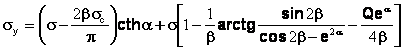(18)

unde:

La varful fisurii, pentru x=a₁, rezulta a=0, iar conform conditiei lui Dugdale, s=s_c , rezulta , iar prima paranteza se anuleaza.

Pentru si iar Q este neglijabila, tensiunea s_y devine:

(19)

Pentru , deplasarea unui punct al fisurii va fi:

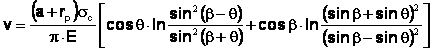(20)

in care : , iar

Pentru x=a , in varful fisurii reale, b q, iar deplasarea la varful fisurii este:

(21)

Se dezvolta in serie Mac Laurin functia sec b , iar si rezulta:

(22)

Daca raportul , din dezvoltarea in serie se retine numai primul termen, iar deplasarea va fi:

(23)

Se introduce notatia d = 2v_v, se considera corelatiile cu factorul de intensitate a tensiunii si cu tenacitatea ruperii si se va obtine:

Marimea d reprezinta deplasarea de deschidere a fisurii, fiind un parametru fundamental al mecanicii ruperii si este utilizat impreuna cu tenacitatea G si cu factorul de intensitate a tensiunii K.

Daca s s_c

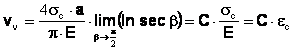(24)

iar C este o constanta. Deci, cresterea deplasarii la varful fisurii v_v este proportionala cu cresterea alungirii specifice e_c , relatia (25):

(25)