Conductia stationara prin pereti sferici

Conductia stationara prin pereti sferici

Pentru a determina fluxul de caldura prin pereti sferici consideram un volum definit de doua sfere de raze si , conform figurii 7.24:

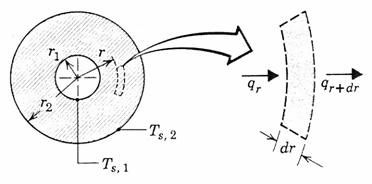
Fig. 7.24

La distanta r se defineste o suprafata sferica de grosime dr. Fluxul termic pe fata interioara a acesteia este , iar pe fata exterioara este .

Expresia fluxului termic este data de legea lui Fourier, in care suprafata A este particularizata pentru cazul unei suprafete sferice de raza

(7.67)

Pentru suprafata sferica definita mai sus, se integreaza ecuatia definita de formula (7.67). Observam ca ecuatia diferentiala se poate integra prin separarea variabilelor.

(7.68)

Integrand ecuatia (7.68), rezulta

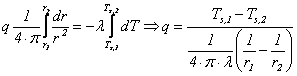(7.69)

Daca ne referim la analogia electrica, rezistenta termica conductiva asociata unui perete sferic definit de razele si este, conform relatiei (7.69), urmatoarea:

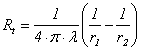(7.70)

Elemente de conductia nestationara

Ecuatia difuziei caldurii, in diverse sisteme de coordonate, este alcatuita din termeni ce contin derivatele temperaturii functie de coordonate si un termen care contine derivata temperaturii functie de timp. Pentru a obtine solutii analitice, se introduc ipoteze simplificatoare, cea mai utilizata fiind aceea prin care se considera campul de temperatura stationar, lucru ce face posibil anularea termenului ce contine derivata temporara a temperaturii.

In cazul cand se doreste obtinerea de solutii luand in considerare termenul ce contine derivata temporara a temperaturii, solutiile vor fi de forma , campul de temperatura depinde atat de coordonatele spatiale, cat si de timp. Spunem ca avem o solutie nestationara a ecuatiei difuziei caldurii, care defineste campul de temperatura in timp si in spatiu.

Datorita formei complexe a ecuatiei difuziei caldurii, solutiile analitice sunt limitate, iar acestea sunt obtinute in conditiile unor ipoteze simplificatoare. Solutii complexe, fara a introduce ipoteze simplificatoare, se pot obtine pe cale numerica.

5.1 Metoda capacitatii punctiforme

De multe ori, se pot obtine solutii simple pentru transferul nestationar de caldura prin introducerea unor ipoteze ce reflecta o comportare particulara a anumitor corpuri in timpul transferului de caldura, comportare datorata unor proprietati specifice. Astfel, pentru multe corpuri solide, in special metale, caracterizate de valori mari ale conductivitatii, gradientul de temperatura in interiorul corpului in timpul transferului de caldura este mic, lucru ce permite introducerea unei ipoteze simplificatoare prin care se considera ca temperatura corpului este uniforma. Practic, prin aceasta ipoteza dispare efectul spatial al volumului corpului, acesta putand fi considerat punctiform. Aceasta ipoteza sta la baza metodei capacitatii punctiforme.

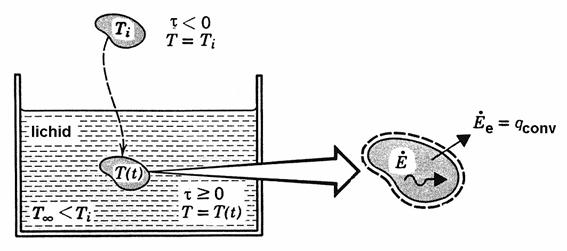
Fig. 7. 25

Pentru a explica metoda capacitatii punctiforme, consideram un bucata de metal calda, cu temperatura initiala , racita intr-un lichid cu temperatura (fig. 7.24). Ipoteza de baza a metodei presupune ca temperatura corpului metalic este uniforma in volumul acestuia, pe intreaga durata a procesului. Initial, temperatura metalului este ; dupa ce acesta este introdus in vasul cu lichid, temperatura corpului se va modifica in timp. Utilizarea ipotezei prin care temperatura corpului este uniforma in intregul volum face ca temperatura corpului sa devina o functie de o singura variabila: timpul.

Bilantul puterilor termice pe volumul de control asociat corpului (fig. 7.24) ne arata ca variatia energiei corpului este egala cu puterea termica transmisa prin convectie lichidului:

(7.71)

sau:

(7.72)

Relatia (7.72) reprezinta ecuatia diferentiala ce descrie variatia in timp a temperaturii corpului.

Se introduce notatia

(7.73)

Cu aceasta notatie, ecuatia devine

(7.74)

Prin integrare, obtinem

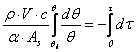unde (7.75)

Solutia este

(7.76)

sau :

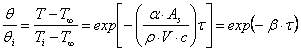(7.77)

Coeficientul timpului din ecuatia (7.77) se noteaza cu si se numeste constanta termica a timpului.

(7.78)

Din relatia de mai sus se determina constanta termica a timpului; ea este egala cu produsul dintre rezistenta termica convectiva si capacitatea termica punctiforma a solidului. Aceste marimi determina raspunsul in timp al corpului.

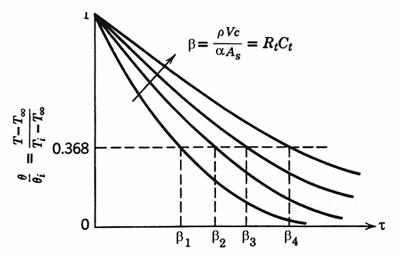
Fig. 7.26

In figura 7.25 sunt prezentate grafic cateva solutii ale ecuatiei (7.77). Se observa influenta constantei termice a timpului . practic, aceasta constanta modifica raspunsul in timp al corpului.

Fiind vorba de un fenomen dinamic, exista un circuit electric echivalent ce permite modelarea fenomenelor de transfer nestationar de caldura

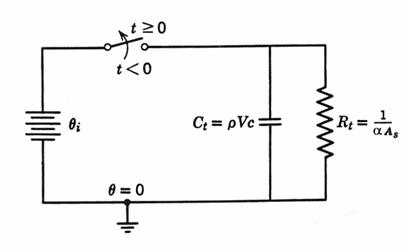
Fig. 7.27

In figura 7.26 este prezentat circuitul electric echivalent, impreuna cu echivalenta marimilor. Practic, timpul de descarcare al condensatorului prin rezistenta este similar cu timpul de raspuns al corpului racit.

Exemplul E 7.5

Un termocuplu ce poate fi asimilat unei sfere este folosit pentru masurarea temperaturii intr-un gaz. Coeficientul de convectie este 400 W/m²/K, iar proprietatile materialului sunt caldura specifica c=400 J/kg/K si densitatea r=8500 kg/m³ .

Sa se determine diametrul termocuplului, astfel incat constanta termica a timpului sa fie de 1s. Daca termocuplul, de la 25 , este introdus in curentul de gaz la 200 C, cat timp ii trebuie termocuplului sa ajunga la 199 C

Solutie

Din conditia deducem diametrul termocuplului

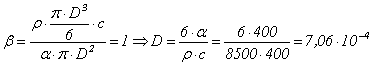m

Din ecuatia (7.77) determinam timpul

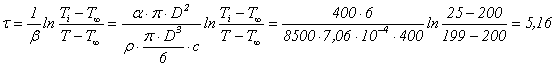s

5.2 Analiza metodei capacitatii punctiforme

Consideram un transfer de caldura stationar, printr-un perete de latime L. Una dintre suprafete este mentinuta la temperatura , iar cealalta suprafata este expusa unui curent de fluid la temperatura , astfel incat temperatura acestei fete este , cu conditia (fig. 7.27).

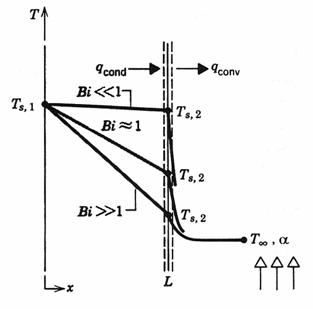
Fig. 7.28

Bilantul puterilor pe fata exterioara a peretelui este

(7.79)

Rearanjand relatia de mai sus, obtinem 

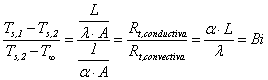(7.80)

Relatia de mai sus ne arata ca raportul rezistentelor termice conductive si convective este adimensional si poarta numele de numarul lui Biot (sau criteriul lui Biot, referitor la criterii de similitudine). Acesta joaca un rol fundamental in problemele de conductie ce au o suprafata conductiva.

Prin analiza numerica a schimbului de caldura, conform schemei din figura 7.27, rezulta ca pentru valori ale numarului lui Biot mult mai mici ca 1 (Bi << 1), rezistenta conductiva a peretelui este mai mica decat rezistenta convectiva din stratul limita al fluidului. In aceste conditii, se poate aplica metoda capacitatii punctiforme.

Din figura 7.27 se observa ca, in acest caz, variatia de temperatura in interiorul peretelui este mica.

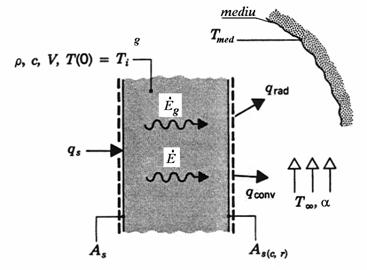
Fig. 7.29

Se considera un caz general (fig. 7.28) al unui perete, care pe o fata are impus un flux termic , iar pe cealalta fata este in contact cu un fluid, astfel incat exista un flux de caldura convectiv si unul radiant . Temperatura fluidului este , iar temperatura mediului exterior este . In interiorul peretelui se genereaza caldura de o sursa de intensitate .

Aplicand conservarea puterilor termice, obtinem urmatoarea ecuatie

(7.81)

(7.82)

Ecuatia (7.82) este o ecuatie diferentiala de ordinul unu, neomogena si neliniara, ce nu are solutie analitica. Ea poate fi integrata numeric, dar - utilizand anumite ipoteze simplificatoare - putem obtine si solutii analitice.

Daca fluxul termic impus este nul, fluxul generat in perete este nul si convectia poate fi neglijata, . acesta poate fi cazul unui perete supus unei intense radiatii (flacara); ecuatia se simplifica si ajunge la forma:

(7.83)

Separand variabilele si integrand, obtinem

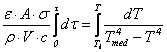(7.84)

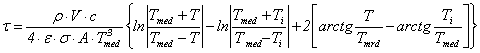(7.85)

O alta solutie exacta se poate obtine in conditiile in care fluxul termic radiant este nul. Se introduce temperatura redusa , precum si urmatoarele notatii

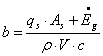; (7.86)

In aceste conditii, ecuatia (7.82) devine 

(7.87)

Solutia generala a ecuatiei (7.87) se obtine prin insumarea solutiei ecuatiei omogene si a solutiei particulare. Neomogenitatea se elimina prin introducerea transformarii:

(7.88)

Ecuatia (7.87) devine:

(7.89)

Separand variabilele si integrand intre si , rezulta solutia:

(7.90)

Revenind la variabilele initiale, obtinem 

In final, rezulta

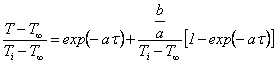(7.92)

Solutii exacte pentru ecuatia difuziei caldurii in cazul

unui corp solid, semiinfinit

Metoda capacitatii punctiforme se aplica intr-un numar limitat de cazuri, care indeplinesc ipotezele respective. Pentru determinarea spatial-temporara a campului de temperatura in interiorul unui solid, trebuie sa utilizam ecuatia difuziei caldurii. Deoarece aceasta ecuatie este complicata, solutiile analitice care se pot obtine sunt limitate.

Daca consideram ecuatia (7.25) si introducem urmatoarele ipoteze simplificatoare: conductie este monodimensionala si fara surse de caldura, obtinem urmatoarea forma:

(7.93)

Aceasta forma simpla permite obtinerea de solutii analitice daca se integreaza pe un domeniu semiinfinit, rezultand campul de temperatura sub forma unei suprafete definita de functia .

Domeniul de integrare este monodimensional omogen, pornind de la pana la . Integrarea se face de la momentul pana la momentul . Conditia initiala o reprezinta precizarea temperaturii pentru toate valorile lui x la momentul si este reprezentata de relatia .

In figura 7.29 sunt prezentate trei tipuri de conditii la limita, pentru limita din stanga a domeniului reprezentata de ecuatia , ce se pot utiliza pentru ecuatia (7.93)

prima conditie este de tip Dirichlet si se refera definirea unei temperaturi pe suprafata din stanga a domeniului, pentru orice valoare a timpului;

a doua conditie este de tip Neumann si se refera la impunerea unui flux de caldura constant , pentru toate valorile timpului

a treia conditie se refera la cazul cand suprafata din stanga domeniului este in contact cu un fluid in miscare; in acest caz conditia la limita este tot de tip Neumann, prin care derivata temperaturii in punctul , inmultita cu conductivitatea mediului, trebuie sa fie egala cu fluxul termic convectiv. Aceasta conditie la limita este variabila functie de valoarea timpului , deoarece in ecuatia respectiva apare valoarea momentana a temperaturii la limita domeniului .

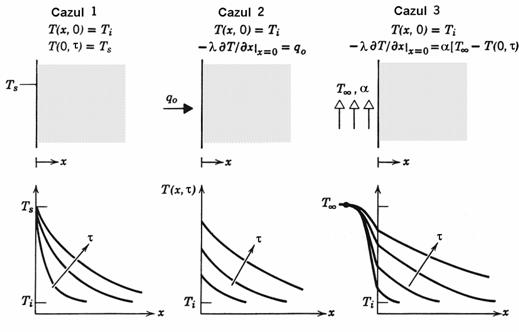
Fig. 7.30

Solutiile obtinute pentru ecuatia (7.93), pentru cele trei cazuri, sunt reprezentate grafic in figura 7.2. analitic, au urmatoarele formulari

Cazul 1

in acest caz, fluxul termic pentru este

(7.95)

Cazul 2

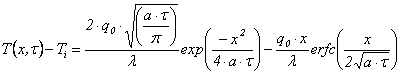
Cazul 3

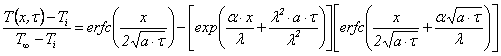
S-a notat cu erf functia erorilor a lui Gauss, care se gaseste tabelata in anexa 5, iar cu erfc functia complementara a erorilor, definita astfel

Exemplul E 7.6

Sa se determine adancimea minima la care trebuie ingropata o conducta de apa, astfel incat dupa 60 de zile sa ajunga de la o temperatura de 20 C la 0 C. Pe toata aceasta perioada, temperatura atmosferica se va considera -15 . Pentru sol se dau urmatoarele marimi

 ;  ;  ;

Solutie

In figura 7.30 este prezentata schema conductei:

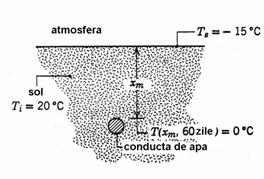
Fig. 7.31

Problema se incadreaza in cazul 1. Fie adancimea la care este ingropata conducta. Dupa 60 de zile, solul are la suprafata -15 C, iar la adancimea conductei 0 C. Suprafata solului constituie inceputul domeniului de integrare, , locul in care se pune conditia la limita , adica temperatura solului la suprafata este egala cu temperatura atmosferica.

Relatia (7.94) ne permite sa calculam temperatura la orice adancime si la orice moment de timp, deci

S-a utilizat pentru functia erorilor, , anexa 5.