| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Constructia inelului Z
1. Notiunea de grup. Grup abelian
Spunem ca o multime M este o structura algebrica, daca pe M s-au definit una sau mai multe operatii (legi de compozitie) si, eventual alte tipuri de relatii binare, care satisfac un numar de axiome, numite axiome de structura.
Definitia 1.1 Se numeste grup o pereche (G, , in care G este o multime nevida, iar " " o lege de compozitie interna pe G, si care satisface axiomele:
(x y) z=x (y z).
x e=e x=x
x x'=x' x=e
adica orice element din G este simetrizabil.
x y=y x
grupul (G, se numeste comutativ sau abelian.
Observatia 1.2: Multimea numerelor intregi Z inzestrata cu operatia de adunare, notata "+", formeaza o structura de grup abelian (Z,+), dar fata de inmultire Z nu are structura de grup, deoarece nu satisface axioma 3.
2. Notiunea de inel. Inel comutativ. Inel unitar
Pe o multime se pot introduce mai multe legi de compozitie. Un caz important il constituie acela in care o multime este inzestrata cu doua legi de compozitie, legate intre ele printr-o anumita proprietate. In acest context se inscrie conceptul (structura) de inel. In continuare vom lua in considerare ca legi de compozitie operatiile de adunare (+) si inmultire ( ), fara a uita insa ca, in general, legile de compozitie pot fi niste operatii oarecare.
Definitia 2.1 Fie I o multime nevida, inzestrata cu doua legi de compozitie pe I. Spunem ca I are o structura de inel in raport cu operatiile de adunare (+) si inmultire ( ), daca sunt satisfacute urmatoarele axiome:
x yII.
x(y+z)=xy+xz si (y+z)x=yx+zx.![]()
Inelul I va fi notat cu (I,+, , punand in evidenta in acest fel rolul diferit al celor doua operatii, prima operatie fiind intotdeauna cea fata de care multimea I are structura de grup comutativ.
Dupa cum se vede din definitia data, multimea I are o structura mai saraca cu privire la cea de-a doua operatie, cea multiplicativa, deoarece se cere sa fie satisfacuta numai proprietatea de parte stabila. Operatia multiplicativa poate avea insa si alte proprietati pe langa aceasta.
Definitia 2.2 Inelul (I,+, se numeste inel asociativ, daca legea de compozitie multiplicativa ( ) este asociativa, adica pentru orice x, y, zII, avem
(x∙y)∙z=x∙(y∙z)
Definitia 2.3 Inelul (I,+, se numeste inel comutativ, daca legea de compozitie multiplicativa este comutativa, adica pentru orice x, yII, avem
x y=y x
Definitia 2.4 Inelul (I,+, se numeste inel unitar (inel cu element unitate) daca legea de compozitie multiplicativa are element unitate, adica exista un element notat cu 1, 1II, astfel incat, pentru orice xII avem
x x
Se intelege ca un inel (I,+, poate fi inel asociativ, comutativ si cu element unitate, spre exemplu multimea numerelor intregi Z formeaza inel comutativ si cu element unitate in raport cu adunarea si inmultirea numerelor intregi.
3. Multimi echivalente. Numere naturale. Operatii cu numere naturale
3.1 Multimi echivalente
Definitia 3.1.1 Doua multimi: A compusa din elementele: a, b, c, . si B compusa din elementele: se numesc echivalente atunci cand elementele lor se pot asocia in perechi:
(a ; (b, ; (c,
astfel incat nici un element din cele doua multimi sa nu scape acestei asocieri si nici unul sa nu se gaseasca in doua perechi. O asemenea relatie intre cele doua multimi este o relatie de echivalenta si se noteaza A~B.
Din felul cum a fost definita relatia rezulta urmatoarele proprietati:
determinarea: A~B sau A B
reflexivitatea: A~A;
simetria: A~B implica B~A;
tranzitivitatea: daca A~B si B~C, atunci A~C.
Aceasta relatie de echivalenta imparte multimile in clase de echivalenta in felul urmator: doua multimi fac parte din aceeasi clasa daca sunt echivalente, in caz contrar, ele apartin la clase diferite. O clasa este caracterizata de o proprietate comuna tuturor multimilor care o compun, proprietate independenta de natura elementelor acestor multimi. Aceasta proprietate este puterea clasei, numarul cardinal, sau marimea clasei.
3.2 Numere naturale
Definitia 3.2.1 Numim numar natural o clasa de echivalenta de multimi finite (o multime se numeste finita daca nu este de aceeasi putere cu nici una din submultimile sale proprii).
Astfel, proprietatea caracteristica a tuturor multimilor compuse dintr-un singur element, care formeaza clasa de echivalenta respectiva se numeste unu si se scrie 1. Proprietatea caracteristica a clasei de echivalenta formata din multimile care contin un element si inca un element se numeste doi si se scrie 2 etc.
In felul acesta se formeaza multimea N a numerelor naturale, care este compusa din elementele:
; 2; 3; .; n; . ,
la care s-a adaugat si zero inaintea numarului 1. Zero este notat cu 0 si caracterizeaza clasa de echivalenta a multimii vide.
Multimea N satisface urmatoarele cinci axiome ale lui Peano:
3.3 Axiomele lui Peano
Zero este un numar natural.
Orice numar natural n are un succesor, pe care il notam n+.
Zero nu este succesorul nici unui numar natural.
Doua numere naturale care au acelasi succesor sunt egale.
Daca A este o submultime a lui N (AÌN), care contine pe zero (0IA) si care daca contine pe n va contine si pe succesorul n+, atunci A=N.
Intre elementele multimii N se pot stabili legi de compozitie interna (sau operatii interne). Astfel, fiecarei perechi ordonate (a,b) apartinand multimii produs N N ii putem face sa corespunda un element c, apartinand lui N, cu ajutorul unei legi de compozitie interna, numita adunare.
3.4 Operatii cu numere naturale
Definitia 3.4.1 Adunarea notata prin + este definita prin recurenta cu ajutorul urmatoarelor doua proprietati:
n+0=n
n+p+=(n+p)+
Din aceste relatii rezulta ca:
n+=n+1
Intr-adevar, avem:
n+1=n+0+=(n+0)+=n+.
Proprietatea a doua se mai poate scrie astfel:
n+(p+1)=(n+p)+1
ceea ce exprima ca, daca n+m este definita pentru m=p, ea se deduce si pentru m=p+1, rezultand ca m+n este determinata pentru orice m.
3.5 Proprietatile adunarii
Teorema 3.5.1: Au loc urmatoarele afirmatii:
Adunarea este asociativa, adica: oricare ar fi n, p, rIN
(n+p)+r=n+(p+r)
Demonstratie: Egalitatea se verifica pentru r=0:
(n+p)+0=n+p si p+0=p, deci (n+p)+0=n+(p+0)=n+p.
Sa aratam ca daca egalitatea este adevarata pentru r, va fi adevarata si pentru r+. Avem:
(n+p)+r+=[(n+p)+r]+=[n+(p+r)]+=n+(p+r)+=n+(p+r+).
Egalitatea este adevarata pentru orice rIN
Adunarea este comutativa, adica: oricare ar fi n, pIN
n+p=p+n
Demonstratie: Demonstram mai intai pentru p=0, oricare ar fi nIN Avem:
n+0=n;
sa aratam ca
+n=n.
Aceasta egalitate este verificata pentru n=0. Sa aratam ca daca este verificata pentru n este de asemenea verificata pentru n+. Avem:
+n+=(0+n)+=n+.
Prin urmare, pentru orice element nIN avem:
n+0=0+n=n.
Sa aratam acelasi lucru pentru p=1, astfel incat sa avem:
n =n+1=1+n.
Trebuie sa aratam ca egalitatea:
1+n=n+1
este adevarata, pentru orice numar natural n. Ea este adevarata pentru n=0. Presupunem ca este adevarata si pentru n, adica
1+n=n+1
si demonstram ca este adevarata si pentru n+. Din:
1+n=n+1 rezulta (1+n)+=(n+1)+,
doua numere naturale egale au acelasi succesor. Avem:
(1+n)+=1+n+ si (n+1)+=n+1+=n+(1+1)=(n+1)+1=n++1.
Deci ipoteza 1+n=n+1 implica n++1=1+n+. Egalitatea 1+n=n+1 este adevarata, pentru orice numar natural. Sa demonstram ca egalitatea
p+n=n+p
care am vazut ca este adevarata pentru orice n, daca p este egal cu 0 sau 1, este verificata de orice p numar natural. Presupunem ca este adevarata pentru p, adica:
p+n=n+p,
de unde:
(p+n)+=(n+p)+.
Avem:
(p+n)+=n+p+=p+(n+1)=p+(1+n)=(p+1)+n=p++n.
De asemenea avem:
(n+p)+=n+p+.
Prin urmare,
n+p+=p++n
Deci egalitatea
n+p=p+n
este verificata oricare ar fi numerele naturale n si p.
3.6 Inmultirea numerelor naturale
Alta operatie interna pe multimea numerelor intregi este inmultirea.
Definitia 3.6.1 Fiecarei perechi ordonate (n,p) de numere naturale ii putem face sa-i corespunda un numar natural numit produs, pe care il notam np, n p sau n p
Aceasta corespondenta este o lege de compozitie interna sau o operatie interna numita inmultire, notata cu (un punct) sau
Inmultirea este definita prin urmatoarele doua egalitati:
n
np+=np+n
Teorema 3.6.2: Au loc urmatoarele afirmatii:
Oricare ar fi nIN, avem
n 1=n
Demonstratie: Intr-adevar:
n 1=n 0+=(n 0)+n=n
Suma a p elemente toate egale cu n este egala cu pn
Demonstratie: Dupa definitia inmultirii avem:
n 1+=n 1+n=n+n=2n.
Daca suma
Sp=n1+n2+.+np
unde toti termenii sunt egali cu n este egala cu pn, atunci deducem ca:
Sp+1=Sp+n=np+n=n p+=(p+1)n.
Prin urmare oricare ar fi p avem:
Sp=np
Inmultirea este distributiva fata de adunare, adica oricare ar fi n, p, qIN este adevarata relatia:
n(p+q)=np+nq.
Este adevarata pentru q=0 oricare ar fi n si p:
n(p+0)=np+n 0=np.
O presupunem adevarata pentru q si demonstram ca este adevarata si pentru q+. Avem:
n(p+q+)=n(p+q)+=n(p+q)+n=np+nq+n=np+nq+.
Deci relatia este adevarata oricare ar fi numerele naturale n, p si q.
Inmultirea se mai bucura si de proprietatile de asociativitate si comutativitate, care pot fi dovedite cu ajutorul definitiei si a inductiei complete.
Teorema 3.6.3: Au loc urmatoarele afirmatii:
Operatiile de adunare si inmultire sunt definite pentru orice pereche de numere naturale, adica sunt definite peste tot in multimea N.
Operatia inversa adunarii, scaderea si operatia inversa inmultirii, impartirea nu sunt posibile pentru orice pereche ordonata de numere naturale.
Definitia 3.7.1: Fie doua numere naturale oarecare n si p. Spunem ca p este cel mult egal cu n sau ca n este mai mare sau egal cu p, daca exista un numar natural d, astfel incat
n=p+d
Notam aceasta relatie dintre n si p prin:
n£p sau n³p
Teorema 3.7.2: Fiind date doua numere naturale n si p are loc una si numai una dintre relatiile:
n£p sau n³p
Relatia definita prin simbolul ³ intre elementele multimii N este o relatie de ordine, deoarece este:
reflexiva: n³n
antisimetrica: daca n³p si p³n, atunci n=p;
tranzitiva: daca n³p si p³r, atunci n³r
Multimea N, in care a fost stabilita aceasta relatie, este o multime (total) ordonata.
4. Multimea numerelor intregi
4.1 Constructia multimii numerelor intregi
Vom arata in continuare ca multimea numerelor intregi Z formeaza inel asociativ, comutativ si cu element unitate, in raport cu adunarea si inmultirea numerelor intregi, notat (Z,+,
In multimea numerelor naturale N scaderea nu este intotdeauna posibila. Diferenta n p nu exista decat daca n³p sau, altfel spus, ecuatia
x+p=n
nu are solutii in N decat daca n³p
A lua o pereche de numere n si p, intr-o anumita ordine in multimea N, inseamna a lua un element din multimea produs N N Se pot determina in multimea N N doua submultimi, una P, formata din elementele =(n,p), in care n³p si n-p este un numar natural, alta P', formata din elementele (n',p'), in care n'<p'.
Fie q un numar natural.
Toate elementele multimii N N care pot fi puse sub forma:
p=[(p+q), p]
apartin submultimii P Pentru orice element al acestei submultimi avem:
(p+q) p=q
corespunzand numarului natural q.
Doua elemente ale submultimii P,
(n ,p si α2=(n ,p
care corespund aceluiasi numar natural sunt legate intre
ele printr-o relatie binara ![]() , definita in multimea P prin:
, definita in multimea P prin:
(n1 - p1)IN si (n2 - p2)IN implica a ![]() a , unde:
a , unde:
n1-p1=n2-p2
Egalitatea:
n1 p1=n2 p2
este in multimea P echivalenta cu
n +p2=n2+p1,
dar aceasta egalitate este verificata si de celelalte elemente din N N care nu apartin multimii P
Definim astfel o relatie binara ![]() in N N prin:
in N N prin:
a ![]() 'a daca si numai daca n1+p2=n2+p1.
'a daca si numai daca n1+p2=n2+p1.
Teorema 4.1.1: Relatia ![]() este o relatie de echivalenta.
este o relatie de echivalenta.
Demonstratie: Intr-adevar, relatia este:
reflexiva: a IN N implica a ![]() 'a , deoarece:
'a , deoarece:
n1+p1=n1+p1
simetrica: a ![]() 'a implica a
'a implica a ![]() 'a , deoarece:
'a , deoarece:
n1+p2=n2+p1 implica n2+p1=n1+p2;
tranzitiva: a ![]() 'a implica n1+p2=n2+p1;
'a implica n1+p2=n2+p1;
a ![]() 'a implica n2+p3=n3+p2,
de unde:
'a implica n2+p3=n3+p2,
de unde:
n1+p2=n2+p1 n2+p1=n1+p2 sau
(n1+p3)+(p2+n2)=(n3+p1)+(p2+n2)
(am folosit asociativitatea si comutativitatea adunarii numerelor naturale).
De unde
n1+p3=n3+p1 (regularitatea numerelor naturale in raport cu adunarea).
Avem deci:
a ![]() 'a
'a
Relatia ![]() fiind o relatie de echivalenta determina o partitie a
lui N N in N N/
fiind o relatie de echivalenta determina o partitie a
lui N N in N N/![]() clase de echivalenta. Multimea Z
a acestor clase de echivalenta este multimea numerelor intregi.
clase de echivalenta. Multimea Z
a acestor clase de echivalenta este multimea numerelor intregi.
Notam cu a=![]() clasa de echivalenta (sau numarul intreg) care contine
elementul a=(n,p)IN . Spunem ca a este un reprezentant a lui a.
Orice element poate reprezenta clasa de echivalenta respectiva, determinand-o.
clasa de echivalenta (sau numarul intreg) care contine
elementul a=(n,p)IN . Spunem ca a este un reprezentant a lui a.
Orice element poate reprezenta clasa de echivalenta respectiva, determinand-o.
4.2 Adunarea numerelor intregi
Definitia 4.2.1: Suma a doua elemente ale multimii N N a =(n1,p1) si a =(n2,p2) este un element a =(n3,p3) definit prin
n3=n1+n2, p3=p1+p2.
Adunarea in N N este o lege de compunere interna definita peste tot.
Teorema 4.2.2: Suma a doua elemente a =(n1,p1) si a =(n2,p2) echivalente, respectiv cu a '=(n1',p1') si a '=(n2',p2'), este echivalenta cu suma a a
Demonstratie: Avem:
a a a =(n3,p3),
a a a '=(n3',p3')
in care:
n3=n1+n2, p3=p1+p2,
n3'=n1'+n2', p3'=p1'+p2'.
Numerele a si a sunt echivalente atunci cand:
n3+ p3'=n3'+p3,
adica:
(n1+n2)+( p1'+p2')=(n1'+n2')+( p1+p2).
Primul membru se poate scrie:
(n1+p1')+(n2+p2'),
iar al doilea
(n1'+p1)+(n2'+p2).
Dar a si a sunt echivalente, deci
n1+p1'=n1'+p1,
la fel a si a ' sunt echivalente, deci
n2+p2'=n2'+p2.
Avem:
(n1+p1')+(n2+p2')=(n1'+p1)+(n2'+p2).
Prin urmare cele doua elemente a si a sunt echivalente.
Consecinta 4.2.3: Clasa de echivalenta a sumei a doua elemente din N N depinde de clasa de echivalenta a fiecaruia din aceste elemente, dar nu depinde de reprezentantul ales in fiecare din aceste clase.
Definitia 4.2.4: Se numeste suma a doua numere intregi a1 si a2, care au ca reprezentanti respectiv pe a si a , numarul intreg a3 care admite ca reprezentant (a a
4.3 Proprietatile adunarii numerelor intregi
Teorema 4.3.1: Au loc urmatoarele afirmatii:
Adunarea pe Z este o lege de compozitie interna comutativa.
Demonstratie: Fie: ![]() si
si ![]() . Atunci avem:
. Atunci avem:
![]()
![]() ,
,
deci:
a1+a2=a2+a1.
Adunarea pe Z este o lege de compozitie interna asociativa.
Demonstratie: Fie: ![]() ;
; ![]() ;
; ![]() . Atunci avem:
. Atunci avem:
![]() , unde
, unde 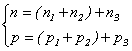 ,
,
![]() , unde
, unde 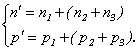
Asociativitatea numerelor naturale implica:
n=n' si p=p'
deci:
[(a1+a2)+a3]=[a1+(a2+a3)],
ca avand acelasi reprezentant.
Adunarea pe Z admite (un) element neutru.
Demonstratie: Fie elementul e![]() ; avem:
; avem:
![]() ,
,
oricare ar fi n, deoarece
n+0=0+n.
Fie ![]() ; avem:
; avem:
![]()
Deci e este element neutru pentru adunare.
Fiecare element din Z are un simetric (sau opus) fata de operatia de adunare pe Z.
Demonstratie: Oricarui element ![]() ii putem face sa-i
corespunda un element
ii putem face sa-i
corespunda un element ![]() , astfel incat:
, astfel incat:
![]()
In multimea Z in care s-a definit operatia adunarii, care este asociativa, fiecare element poseda un simetric (opus) si unul singur. Notam cu a simetricul lui a.
Teorema 4.3.2: Simetricul (opusul) sumei este egal cu suma simetricelor (opusilor).
Demonstratie: Notand cu a' si b' simetricii lui a si b, avem:
(a+b)+(a'+b')= (a+b)+a']+b'=[a+a'+b]+b'=(e+b)+b'=b+b'=e.
Teorema 4.3.3: Ecuatia
x+b=a, a, bIZ
admite in Z o singura solutie si numai una.
Demonstratie: Daca x exista, notand cu b' simetricul lui b avem:
(x+b)+b'=b'+a=x+(b+b')=x+e=x,
deci daca x exista si el este egal cu b'+a.
Dar oricare ar fi a si b avem:
(b'+a)+b=a+(b'+b)=a.
Ecuatia admite o singura radacina:
x=b'+a.
4.4 Grup abelian in raport cu adunarea
Multimea numerelor intregi Z, pe care s-a stabilit operatia de adunare, formeaza un grup, deoarece adunarea poseda urmatoarele trei proprietati:
Este asociativa;
Admite un element neutru e=(0,0);
Orice element a, al multimii Z, are un simetric a' (in cazul adunarii, un opus).
Adunarea este si comutativa, deci formeaza un grup comutativ sau abelian.
4.5 Inmultirea numerelor intregi
Definitia 4.5.1: Numim produs a doua elemente (n1,p1) si (n2,p2) elementul (n3,p3), in care:
n3=n1n2+p1p2 si p3=n1p2+n2p1.
Teorema 4.5.2: Operatia de inmultire in N N pastreaza relatia de
echivalenta ![]() .
.
Demonstratie: Pentru a demonstra aceasta este suficient sa inlocuim un element (n1,p1) sau (n2, p2) printr-un element echivalent; vom obtine un produs (n3',p3') echivalent cu (n3,p3).
Inlocuind, de exemplu, pe (n2',p2') obtinem:
![]() unde
unde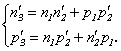
a3 si a3' sunt echivalente daca
n3+p3'=n3'+p3;
avem:
n3+p3'=n1n2+p1p2+n1p2'+n2'p2=n1n2+p2'+p1p2+n2'
n3+p3'=n1n1'+p1p2'+n2p1+n2p1=n1n1'+p2+p1p2'+n2
dar (n2,p2) si (n2',p2') sunt echivalente. Avem deci
n2+p2'=n2'+p2,
de unde
n3+p3'=n3'+p3,
deci (n3,p3) si (n3',p3') sunt echivalente apartinand aceleiasi clase de echivalenta.
Consecinta 4.5.3: Oricare ar fi reprezentantii alesi a celor doua clase de echivalenta a1 si a2, produsul acestor reprezentanti apartin unei aceleiasi clase de echivalenta a.
Aceasta clasa de echivalenta a o vom numi produsul intregilor a1 si a2 si o vom nota
a=a1a2 sau a1a2.
Avem:
![]() .
.
4.6 Proprietatile inmultirii numerelor intregi
Teorema 4.6.1: Au loc urmatoarele afirmatii:
Inmultirea numerelor intregi este o operatie comutativa.
Demonstratie: Avem:
![]() si
si
![]() ,
,
deci:
a1a2=a2a1
Inmultirea numerelor intregi este o operatie asociativa, adica:
(a1a2)a3=a1(a2a3)
ceea ce rezulta inlocuind a1,a2,a3
prin ![]() si efectuand
calculele.
si efectuand
calculele.
Elementul ![]() este element neutru
pentru inmultirea numerelor intregi.
este element neutru
pentru inmultirea numerelor intregi.
Demonstratie: Oricare ar fi ![]() , avem:
, avem:
![]()
Inmultirea numerelor interegi este o operatie distributiva in raport cu adunarea.
Demonstratie: Punand: ![]() ,
,
avem:
![]() , unde:
, unde:
n=n1[n2+n3]+p1[p2+p3]
p=n1[p2+p3]+p1[n2+n3]
Pe de alta parte avem:
![]() , unde:
, unde:
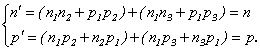
Rezulta ca:
a1(a2+a3)=a1a2+a1a3
4.7 Inelul numerelor intregi
In multimea numerelor intregi Z am stabilit doua legi de compozitie interna: una numita adunare, care satisface proprietatile unui grup abelian iar cealalta numita inmultire, care satisface urmatoarele proprietati:
asociativitate,
comutativitate,
element neutru si
distributivitate in raport cu adunarea
In acest caz spunem ca multimea numerelor intregi formeaza un inel comutativ si unitar.
BIBLIOGRAFIE
[1] Andrei, GH., Caragea, C., Cucurezeanu, I., Bordea, Gh., Probleme de algebra Editura Didactica si Pedagogica, Bucuresti, 1993.
Andrica D., Duca I. D., Pop I., Purdea I., Matematica de baza, Editura Studium, Cluj-Napoca, 2000.
[3] Beju, A. E., Beju, I., Compendiu de matematica, Editura Stiintifica si Enciclopedica, Bucuresti, 1983.
[4] Busneag, D., Boboc, Fl., Piciu, D., Elemente de aritmetica si teoria numerelor Editura Universitaria, Craiova, 1999.
[5] Popovici, C. P., Teoria numerelor, Editura Didactica si Pedagogica, Bucuresti, 1973.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1839
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved