Exercitii si probleme rezolvate - statistica

Exercitii si probleme rezolvate

Se considera un esantion de 20 de clienti, care intra intr-un magazin alimentar, pentru a cerceta frecventa X cu care clientii fac apel la serviciile magazinului de-a lungul unei saptamani si respectiv pentru cercetarea cheltuielilor lunare Y in mii lei, ale clientilor pentru procurarea de bunuri alimentare. S-au obtinut urmatoarele date de selectie pentru X si respectiv Y

X

Y

Se cere:

a)      distributiile empirice de selectie pentru fiecare din caracteristicile X si Y,

b)      mediile de selectie, momentele centrate de selectie de ordinul al doilea si dispersiile de selectie pentru caracteristicile X si Y,

c)      functiile de repartitie de selectie pentru X si Y.

Solutie. a) Se observa ca datele de selectie pentru caracteristica X au numai N = 6 valori distincte, deci distributia empirica de selectie pentru X este

.

Pentru caracteristica Y toate datele de selectie sunt distincte. Asadar, distributia empirica de selectie a lui Y este un tablou in care pe o linie sunt trecute toate aceste valori (eventual ordonate crescator), iar pe linia a doua se trec frecventele acestor valori, care sunt toate egale cu 1. Vom face o grupare a datelor de selectie corespunzatoare caracteristicii Y. Anume, prima clasa cuprinde cheltuielile lunare de la 80-89 mii lei, etc. Dupa efectuarea acestei grupari, distributia empirica de selectie a lui Y devine

.

b) Mediile de selectie pentru cele doua caracteristici sunt respectiv

,

mii lei.

Daca se folosesc datele grupate pentru caracteristica Y se obtine

mii lei .

Valorile momentelor centrate de selectie de ordinul doi pentru cele doua caracteristici sunt respectiv

,

.

Pentru simplificarea calculelor, se poate folosi formula

,

unde a este o constanta reala convenabil aleasa. Anume, daca pentru caracteristica X vom alege a = 3, atunci

.

Pentru caracteristica Y vom lua a = 105, obtinandu-se astfel

.

Se observa ca s-a calculat cu datele de selectie grupate, ceea ce conduce la o valoare putin diferita de valoarea ce s-ar obtine cand se lucreaza cu datele de selectie primare (negrupate).

Valorile dispersiilor de selectie pentru caracteristicile X si Y se calculeaza imediat, daca se cunosc momentele centrate de selectie de ordinul doi, anume

,

respectiv

.

Astfel se poate obtine si respectiv mii lei.

c) Functiile de repartitie de selectie pentru cele doua caracteristici sunt respectiv

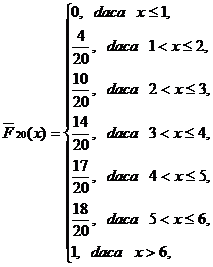
pentru caracteristica X si

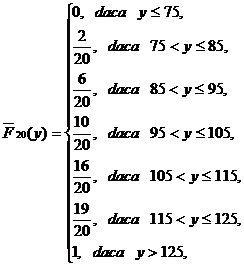
pentru caracteristica Y.

La un control de calitate se verifica diametrul pieselor prelucrate de un strung. Pentru realizarea acestui control s-a considerat o selectie de 18 piese si s-a obtinut ca diametrul X al pieselor are urmatoarele dimensiuni (in cm):

Sa se determine:

a)      o estimatie absolut corecta pentru diametrul mediu al pieselor realizate,

b)      o estimatie corecta si una absolut corecta pentru dispersia diametrelor fata de diametrul mediu.

Solutie. a) Distributia empirica de selectie a caracteristicii X este

.

Diametrul mediu este media teoretica . Dar se cunoaste ca un estimator absolut corect pentru media teoretica m este media de selectie . Prin urmare, valoarea mediei de selectie este o estimatie absolut corecta pentru media teoretica . In cazul de fata se obtine

.

b) Deoarece un estimator corect al dispersiei teoretice este momentul centrat de selectie de ordinul doi, adica , rezulta ca o estimatie corecta pentru dispersia teoretica este valoarea momentului centrat de selectie de ordinul doi, adica

,

unde constanta reala a este convenabil aleasa. Asadar, in cazul de fata, o estimatie corecta a dispersiei diametrelor fata de diametrul mediu este

.

Imediat avem o estimatie absolut corecta pentru dispersia teoretica, anume

.

Fie caracteristica X ce urmeaza legea normala N (m,s), unde m I R este cunoscut, iar s > 0 este necunoscut. Se considera o selectie repetata de volum n. Sa se arate ca functia de selectie

este o functie de estimatie absolut corecta pentru parametrul

Solutie. Vom arata ca sunt satisfacute cele doua conditii din definitia functiei de estimatie absolut corecte, adica

M(V) = s si lim D² (V) = 0

In primul rand avem ca:

Deoarece caracteristica X urmeaza legea normala N(m, s) avem ca

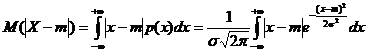
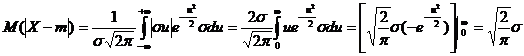
Daca se face schimbarea de variabila si se tine seama de faptul ca functia de integrat obtinuta, dupa aceea, este functie para, rezulta ca :

Prin urmare, obtinem ca M(V)= = s, deci prima conditie este satisfacuta.

Pentru verificarea celeilalte conditii putem scrie succesiv:

de unde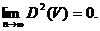

Se considera caracteristica X ce urmeaza legea binomiala, adica are distributia teoretica

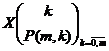, unde P(m,k)=C^k_mp^kq^m-q, q=1-p,

cu parametrul p I (0,1) necunoscut. Folosind o selectie de volum n, se cere

a)      estimatorul p* de verosimilitate maxima pentru p,

b)      sa se arate ca etimatorul p* este un estimator absolut corect pentru parametrul p

c)      sa se arate ca estimatorul p* este un estimator eficient pentru parametrul p.

Solutie. a) Functia de probabilitate pentru caracteristica X este f(x;p)= C^k_mp^x(1-p)^m-x,

Pentru a scrie ecuatia de verosimilitate maxima

avem ca ln f= (x;p)= ln C^x_m + x ln p + (m-X) ln (1-p), de unde

Asadar, ecuatia verosimilitatii maxime este

adica

unde .Ecuatia verosimilitatii maxime se mai scrie

de unde se obtine estimatorul de verosimilitate maxima

pentru parametrul p.

b) Vom arata ca estimatorul p* este un estimator absolut coret pentru parametrul p

Pentru aceasta avem, in primul rand, ca

iar apoi, pentru dispersie se poate scrie succesiv

Asadar, s-a obtinut

M(p*)=p si

deci estimatorul p* este estimator absolut corect pentru parametrul p.

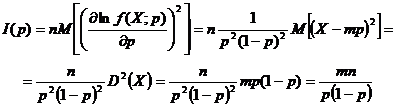
c) Cantitatea de informatie relativa la parametrul p se poate calcula dupa cum urmeaza

Pe de alta parte, am vazut ca prin urmare, are

loc egalitatea deci estimatorul p* este estimator eficient pentru parametrul p.

Relativ la populatia C se cerceteaza caracteristica X privind media teoretica M(X)=m. Stiind ca dispersia teoretica a caracteristicii X este D²(X)=0,35, sa se stabileasca un intreval de incredere pentru media teoretica m cu probabilitatea de incredere 1 - a = 0,95 , utilizand distributia empirica de selectie

Solutie. Deoarece volumul selectiei este n=35 > 30, putem considera ca statistica

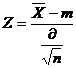
unde

urmeaza legea normala N(0,1). Asadar, intervalul de incredere pentru media teoretica m se obtine din relatia

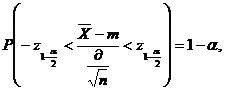
sau

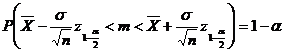
unde astfel determinat incat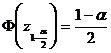

In cazul de fata, valoarea mediei de selectie este:

iar din Anexa I, pentru se gaseste

De asemenea, avem ca

Obtinem in acest fel, intervalul de incredere pentru media teoretica m=M(X)

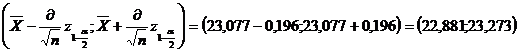
Pentru receptionarea unei marfi ambalata in cutii, se efectueaza un control, prin sondaj, privind greutatea X a unei cutii. Pentru 22 de cutii cantarite s-a obtinut distribuirea empirica de selectie, relativ la caracteristica X:

Folosind probabilitatea de incredere 0,98 sa se determine in interval de incredere pentru valoarea medie a greutatii cutiilor, presupunand ca X urmeaza legea normala N(m, s

Solutie. Deoarece abaterea standard este necunoscuta, se considera statistica

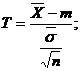
care urmeaza legea Student cu n-1 grade de libertate.

Intervalul de incredere pentru valoarea medie teoretica m= M(X) este

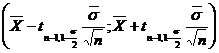
Pentru n - 1 =21 si 1 - a a = 0,02) din Anexa II se

determina

De asemenea, folosind datele de selectie, obtinem valoarea a mediei de selectie , anume:

si valoarea abaterii standard de selectie

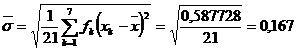
Putem scrie atunci intervalul (numeric) de incredere:

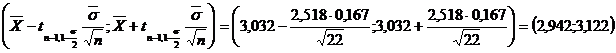
Masa de carne ambalata in pachete de 1000 de grame de masinile M₁ si M₂ este o caracteristica X′, ce urmeaza legea normala N(m′, s′) si respectiv o caracteristica X′′ ce urmeaza legea normala N(m", s

Cantarind 100 de pachete din cele produse de masina M₁ s-a obtinut valoarea medie de selectie grame iar din cantarirea a 150 de pachete de la masina M₂ s-a obtinut grame.

Folosind probabilitatea de incredere 0,98 sa se determine intervalul de incredere pentru diferenta m′-m′′, daca se stie ca abateriile standard sunt s′=3 si s

Solutie. Se foloseste statistica

care urmea

za legea normala N(0,1). Astfel, intervalul de incredere pentru diferenta m′-m′′ este:

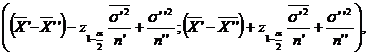
unde
se determina astfel ca 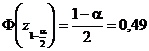Folosind Anexa I, obtinem

De asemenea, avem ca Astfel,

intervalul de incredere pentru diferenta m′ - m′′ este

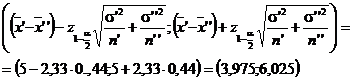
8 Fiecare caracteristica X′ ce urmeaza legea normala N(m′,s) si care reprezinta vanzarile in milioane de lei pe saptamana la magazinele alimentare in orasul A si X" vanzarile in milioane de lei la magazinele alimentare din orasul B si care urmeaza legea normala N(m", s). S-au efectuat doua sondaje, respectiv pentru X′ si X" si s-a obtinut urmatoarele date de selectie:

X′: 226,5 224,1 218,6 220,1 228,8 229,6 222,5

X": 221,5 230,2 223,3 224,3 230,8 223,8

Cu probabilitatea de incredere 0,95 sa se construiasca un interval de incredere pentru diferenta m′-m", daca s > 0 este necunoscut.

Solutie. Folosind statistica

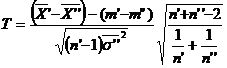
care urmeaza legea Student cu n=n′+n′′-2=7+6-2=11 grade de libertate, se va construi intervalul de incredere pentru m′-m′′. Anume, acest interval de incredere este:

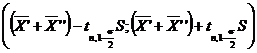
unde, s-a folosit notatia:

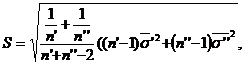
iar se determina astfel incat 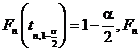fiind functia de repartitie a legii Student cu n grade de libertate, tabelata in Anexa II

Pentru a determina valoarea numerica a intervalului de incredere, se calculeaza pe rand

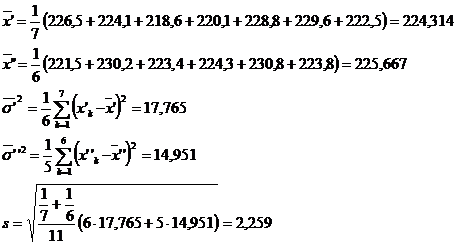
De asemenea, din Anexa II, pentru 1 - a = 0,95 si n = 11, obtinem astfel ca intervalul de incredere pentru m′ - m′′ va fi

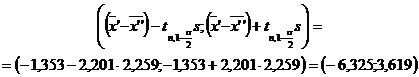
Fie X caracteristica ce reprezinta timpul de producere a unei reactii chimice, masurat in secunde. Daca X urmeaza legea normala N(m,s) si avand o selectie repetata de volum n=11, cu datele de selectie 4,21; 4,03; 3,99; 4,05; 3,89; 3,98; 4,01; 3,92; 4,23; 3,85; 4,20; sa se determine intervalul de incredere pentru dispersia si pentru abaterea standard , cu probabilitatea de incredere 0,95.

Solutie. Se va considera statistica

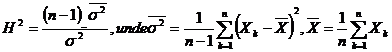
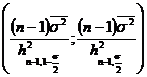
care urmeaza legea χ cu n-1 grade de libertate. Intervalul de incredere pentru s va fi:

iar pentru s

,

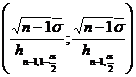unde si se calculeaza din Anexa III.

Pentru determinarea valorilor numerice ale acestor intervale de incredere, calculam:

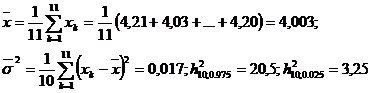
Asadar, intervalele de incredere pentru s² si s sunt

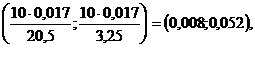
respectiv

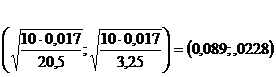
Caracteristica X reprezinta cheltuielile lunare in mii lei pentru abonamentele

la ziare si reviste ale unei familii. Sa se verifice, cu nivelul de semnificatie a=0,01, daca

stim media acestor cheltuieli lunare pentru o familie este de 16 mii lei, stiind ca abaterea standard s =3 mii lei avand o selectie repetata de volum n=40, care ne da distributia empirica de selectie

Solutie. Deoarece n=40>30 si abaterea standard s=3 este conoscuta, vom folosi testul Z pentru verificarea ipotezei nule

H₀ : m= M(X)=16, cu ipoteza alternativa H₁ : m

Pentru a=0,01, folosind Anexa I, se determina astfel incat . Anume, se obtine ca care ne da intervalul numeric (-2,58;2,58), pentru statistica notata prin

Calculam succesiv:

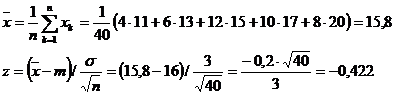
Deoarece , rezulta ca se accepta ipoteza ca cheltuielile medii lunare ale unei familii pentru abonamentele la ziare si reviste sunt de 16 mii lei, cu probabilitatea de risc 0,01.

Caracteristica X reprezinta gradul de ocupare zilnica a unei unitati hoteliere (in procente), Sa se verifice, cu nivelul de semnificatie a=0,05, ipoteza ca media de ocupare zilnica a hotelului este data prin m=80%, daca dintr-o selectie facuta in 15 zile     s-au obtinut urmatoarele date de selectie (in procente) : 60, 85, 90, 75, 84, 78, 92, 55, 77, 82, 65, 79, 83, 65, 76.

Solutie. Putem considera ca X urmeaza legea normala N(m, s ), cu m si s necunoscuti. Ipoteza nula ce se face este H₀ : m = 80, cu H₁ : m

Deoarece abaterea standard s este necunoscuta, se foloseste testul T. Pentru aceasta, considerand a=0,05, cu ajutorul Anexei II, se determina , astfel incat . Se obtine in acest fel . Prin urmare, intervalul pentru statistica T=, care urmeaza legea Student cu n-1=14 grade de libertate, este (-2,145; 2,145).

Calculam in continuare succesisv:

Deoarece ipoteza ca media de ocupare zilnica a unitatii hoteliere este de 80% se accepta

12. La o unitate de imbuteliere a laptelui exista doua masini care efectueaza aceasta operatie in sticle de un litru. Pentru a cerceta reglajul de imbuteliere la cele doua

masini s+au efectuat doua selectii relative la sticlele imbuteliate de cele doua masini si s au obtinut datele de selectie

Folosind nivelul de semnificatie , sa se verifice daca mediile de umplere a sticlelor de catre cele doua masini sunt aceleasi, in cayul in care abaterile standard sunt σ′= 6 ml si ml.

Solutie. Caracteristicile X′ si X" ce reprezinta cantitatea de lapte in ml) continuta de o sticla imbuteliata de prima masina, respectiv de a doua, se considera ca urmand legile de probabilitate normele N (m′, 6) si N (m", 7,5).

Verivicarea ipotezei nule H₀ : m′ = m" cu alternativa H₁ : m′ ≠ m", se va face cu testul Z, deoarece sunt cunoscute abaterile standard.

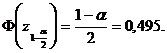Folosind nivelul de semnificatie , se determina din Anexa I valoarea astfel incat Anume, se obtine ca z = 2,58, care ne da intervalul (-2,58; 2,58) pentru statistica :

Se calculeaza succesiv:

.

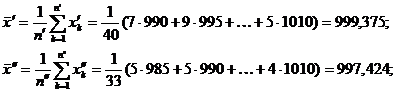
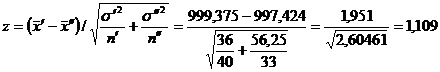Deoarece , rezulta ca mediile de umplere a sticlelor nu difera semnificativ pentru cele doua masini.

13. Se cerceteaza doua loturi de ulei pentru automobile, din punct de vedere al vascozitatii, obtinandu-se datele de selectie

Pentru primul lot:

Pentru al doilea lot:

Analizele facandu-se cu acelasi aparat, se considera ca abaterile standard sunt aceleasi. Considerand nivelul de semnificatie , sa se verifice daca mediile de vascpzitate pentru cele doua loturi nu difera semnificativ.

Solutie: Caracteristicile X′ si X", ce reprezinta vascozitatile pentru cele doua loturi de ulei, se considera ca urmeaza fiecare legea normala, respectiv N (m′, σ) si N (m", σ), cu ambaterea standard σ > 0 necunoscuta.

Verificarea ipotezei nule H₀ : m′ = m" cu alternativa H₁ : m′ ≠ m", se va face cu testul T, deoarece abaterea standard σ este necunoscuta.

Folosind nivelul de semnificatie a=0,05, se determina , din Anexa II, valoarea t_{n,1- (a} astfel incat , unde numarul gradelor de libertate este n=n′+n′′-2=8+8-2=1 Adica, se determina t_14;0;975 astfel incat obtinandu-se t_14;0;975=2,145. In acest mod , s-a obtinut intervalul

(-2,145 ) pentru statistica

,

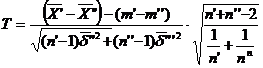care urmeaza legea Student cu n=n′+n′′-2 grade de libertate.

Se calculeaza pe rand

(3 10 +2 2,28+.+1 10,32)=10,285;

(2 10 +2 2,27+.+3 10,31)=10,289;

3,143 10^-4;

4,983 10^-4;

=

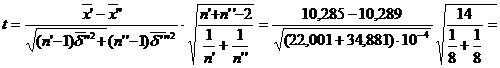
Deoarece t=-0,397 I(-2,145;2,145), rezulta ca vascozitatile medii ale celor doua loturi de ulei nu difera semnificativ.

Se efectueaza o selectie repetata de volum n=12 relativa la caracteristica X ce urmeaza legea normala N(m,d), obtinandu-se distributia empirica de selectie

Sa se verfice , cu nivelul de semnificatie a=0,05, ipoteza nula

H₀ : d =D²(X)=0,5, cu alternativa H₁: d

Solutie Deoarece caracteristica X urmeaza legea normala , pentru verificarea ipotezei nule H_o: d 0,5, se utilizeaza testul c

Pentru nivelul de semnificatie a=0,05, se determina intervalul 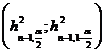, pentru statistica H²=,care urmeaza legea c cu n-1 grade de libertate.

Se utilizeaza Anexa III, pentru a determina intervalul mai inainte precizat. Astfel, deoarece n-1=12-1=11, se obtine =3,82, pentru care F₁₁(3,82)=0,025 si de asemenea =21,9. Prin urmare , intervalul pentru statistica H² este (3,82;21,9).

Se calculeaza succesiv

h²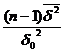⁼==11,396

Deoarece h²=11,396 I(3,82;21,9), ipoteza nula facuta relativ la dispersia teoretica este acceptata.

15 Doua strunguri produc acelasi tip de piese. Caracteristica cercetata este diametrul acestor piese.Se considera doua selectii de volume n′=7 si n′′=9, relative la diametrele pieselor produse de cele doua strunguri. Datele de selectie sunt prezentate prin distributiile empirice de selectie:

si respectiv

Considerand nivelul de semnificatie a=0,05, sa se verifice ipoteza nula H₀:d d′′, cu alternativa H₁: d d′′, daca se presupune ca X′ si X′′ urmeaza legea normala N(m′,d′) si respectiv N(m′′,d

Solutie. Pentru compararea celor doua dispersii , se utilizeaza testul F. Statistica ce se considera in acest caz este F=, care urmeaza legea Snedecor-Fisher cu (m,n)=(n′-1,n′′-1) grade de libertate.

Pentru inceput se determina intervalul (f_m,n;a f_m,n;1-a ), pentru statistica F, folosind Anexa IV.

Anume, se determina f_m,n;a astfel incat F_m,n (f_m,n;a si respectiv f_m,n;1-a astfel incat F_m,n (f_m,n;1-a

Deoarece m=n′-1=7-1=6 si n=n′′-1=9-1=8 , avem pe de o parte ca =0,18. Prin urmare, intervalul de incredere pentru F este (0,18;4,65).

Se calculeaza, apoi, succesiv:

f

Avand in vedere ca f=1,85I(0,18;4,65), rezulta ca ipoteza facuta, privind egalitatea dispersiilor , este admisa.

16. Se cerceteaza capacitatea fiolelor farmaceutice de 100 ml, care provin de la doua fabrici. In acest scop, se considera cate o selectie pentru doua loturi de fiole provenite respectiv de la cele doua fabrici. Selectiile obtinute au distributiile empirice de selectie

respectiv, pentru X":110, 101, 112, 120, 117, 105, 109, 111, 118, 113, 106, 108, 115, 113, 112, 100, 116, 112, 114, 112.

a)      Folosind nivelul de semnificatie a=0,02, sa se compare dispersiile celor doua caracteristici;

b)      Folosind acelasi nivel de semnificatie a=0,02, sa se compare mediile celor doua caracteristici;

Solutie. a ) Vom considera ca cele doua caracteristici X′ si X′′ sunt repartizate normal, respectiv N(m′;d′) si N(m′′;d′′). Se poate aplica testul F, pentru compararea dispersiilor d′² si d

Calculam pe rand:

(1 100+1 101+2 102+.+1 109)=104 ;

111 ;

5 ;

27,537.

Deoarece <, se considera statistica F=, care urmeaza legea Snedecor-Fisher cu (m,n)= (n′′-1,n′-1)=(19,24) grade de libertate.

Daca se considera ipoteza nula

H₀:d d′′², cu alternativa H₁: d d

avem ca f=

Pe de alta parte, pentru a=0,002, avem din Anexa IV, ca

f_m,n;1-a/2= =2,76;

f_m,n;a/2= ==0,3

In acest fel , am obtinut intervalul (0,34;2,76), pentru statistica F.

Deoarece f=5,31 (0,34;2,56),respingem ipoteza d d

b) Avand in vedere ca dispersiile teoretice d′² si d′′² sunt necunoscute, iar comform punctului precedent difera in mod semnificativ, folosim testul T pentru compararea mediilor m′ si m′′. Statistica ce se considera , in acest caz , este:

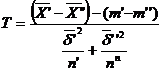
care urmeaza legea Student cu n grade de libertate, unde n se calculeaza din relatia

, cu

Astfel , pentru determinarea lui n, avem succesiv

c=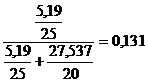 si

de unde n=25.

Folosind Anexa II, se obtine ca t_25;0,99=2,485, prin urmare intervalul pentru statistica T este (-2,485;2,485).

Pe de alta parte ,avem ca

=

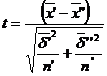Deoarece t=-5,11 (-2,485;2,485), respingem ipoteza ca mediile teoretice pentru fiolele produse de cele doua fabrici nu difera semnificativ.

17. Se considera caracteristica X ce reprezinta rezistenta, in KW, a unor tronsoane de ceramica acoperite de carbon. Sa se verfice normalitatea lui X, folosind o selectie de volum n=124, pentru care s-au obtinut datele de selectie

a) utilizand testul de concordanta c , cu nivelul de semnificatie a

c)      utilizand testul de concordanta al lui Kolomogorov, cu nivelul de semnificatie a

Solutie. Prima data se estimeaza parametrii de la legea normala N(m,d), adica media teoretica m=M(X) si abaterea standard teoretica d , folosind metoda de verosimilitate maxima. Se cunoaste ca estimatiile de verosimilitate maxima pentru m si d sunt respectiv

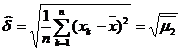
Avem distributia empirica de selectie pentru caracteristica X

de unde calculam

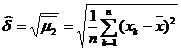
a) Se considera valoarea numerica h²=, unde N este numarul claselor (N=9 in cazul de fata), f_i este frecventa clasei i , iar este dat prin 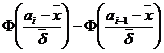, subintervalul [a_i-1,a_i ) definind clasa i. Dupa cum este cunoscut, h² este valoarea unei variabile aleatoare H², care urmeaza legea c cu k=N-s-1 grade de libertate, s fiind numarul parametrilor estimati. In cazul de fata avem ca s=2, deci k=9-2-1=6.

Se determina intervalul (0,), pentru statistica H², folosind Anexa III. Anume, se obtine ca =12,59, adica intervalul pentru statistica H² este (0;12,59).

Calculele pentru valoarea numerica h² se aranjeaza in urmatorul tabel:

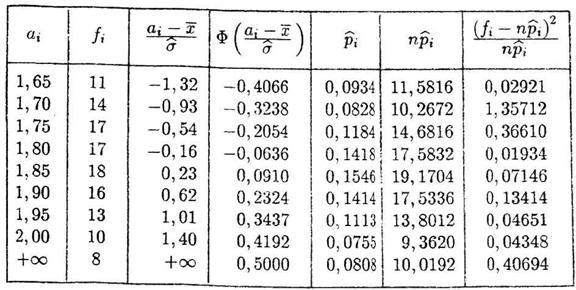
n=124    h²=2,4743

Valorile functiei lui Laplace f se iau din Anexa I si se are in vedere ca f(-x) = -f(x). De asenemea facem observatia ca :

Deoarece h² = 2,4743 I(0; 12,59), rezulta ca se accepta ipoteza normalitatii caracteristicii X.

b) Pentru a = 0.05, folosind Anexa V, se determina x_1-a = x_0.95, astfel incat K(x_1-a a. Se obtine astfel ca x_0.95 = 1,36.

Ipoteza ca X urmeaza legea normala N() , cu si calculati inainte, este acceptata daca , unde

Aici este functia de repartitie de selectie, iar F(x) este functia de repartitie pentru legea normala N

Calculele pentru determinarea lui d_n sunt aranjate in tabelul urmator:

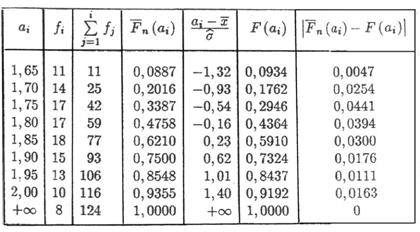
d_n=0,044

Deoarece , acceptam ipoteza ca X urmeaza legea normala N

18. Se tin sub observatie n=50 motoare electrice, pana la defectarea ultimului dintre ele. Se considera caracteristica X, ce reprezinta numarul miilor de ore de functionare pana la defectare. Rezultatele observatiilor sunt grupate in tabelul urmator :

Sa se cerceteze exponentialitatea caracteristicii X folosind:

a) testul c , cu nivelul de semnificatie a

b) testul lui Kolmogorov, cu nivelul de semnificatie a

Solutie : Legea exponentiala are functia de repartitie :

F(x;l)= , x>0 cu parametrul l>0.

Trebuie la inceput sa determinam estimatia de verosimilitate maxima pentru parametrul l. Pentru aceasta, avem ca densitatea de probabilitate corespunzatoare lui F este :

Ecuatia de verosimilitate este :

,

de unde se obtine estimatorul de verosimilitate maxima pentru parametrul l, anume 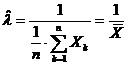. Prin urmare, estimatia de verosimilitate maxima pentru l este

Distributia empirica de selectie pentru X este

de unde obtinem:

astfel ca

a) Se considera valoarea numerica , N fiind numarul

claselor (aici N = 7), f_i este frecventa clasei [a_i-1, a_I), iar Valoarea numerica h² este valoarea unei variabile aleatoare H², care urmeaza legea X² cu k = N- s -1 grade de libertate , s fiind numarul parametrilor estimati , in cazul de fata s = 1 deci k = 7 -1- 1 = 5.

Se determina din Anexa III , astfel incat adica Se obtine astfel ca

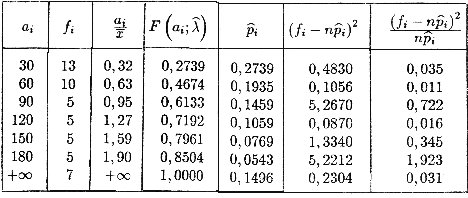
Calculele lui h² se efectueaza din tabelul urmator

n=50 h=3,083

De remarcat cazul particular :

Deoarece , rezulta ca se accepta ipoteza exponentialitatii pentru caracteristica X.

b) Din Anexa V se determina x_1+a = x_0,95 astfel incat sa aiba loc , obtinindu-se x_0,95=1,36.

Ipoteza exponentialitatii lui X este acceptata daca unde fiind functia de repartitie de selectie.

Calculul pentru determinarea lui d_n se efectueaza in tabelul urmator :

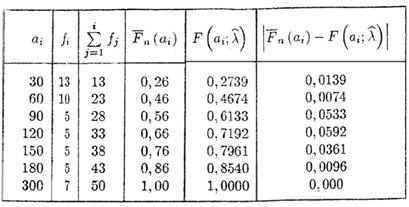
d_n=0,0592

Deoarece acceptam ipoteza ca X urmeaza legea exponentiala.