Inverting matrices

Although in practice we do not generally use matrix inverses to solve systems of linear equations, preferring instead to use more numerically stable techniques such as LUP decomposition, it is sometimes necessary to compute a matrix inverse. In this section, we show how LUP decomposition can be used to compute a matrix inverse. We also discuss the theoretically interesting question of whether the computation of a matrix inverse can be sped up using techniques such as Strassen's algorithm for matrix multiplication. Indeed, Strassen's original paper was motivated by the problem of showing that a set of a linear equations could be solved more quickly than by the usual method.

Computing a matrix inverse from an LUP decomposition

Suppose that we have an LUP decomposition of a matrix A in the form of three matrices L, U, and P such that PA = LU. Using LU-SOLVE, we can solve an equation of the form Ax = b in time (n²). Since the LUP decomposition depends on A but not b, we can solve a second set of equations of the form Ax = b' in additional time (n²). In general, once we have the LUP decomposition of A, we can solve, in time (kn²), k versions of the equation Ax = b that differ only in b.

The equation

AX = I_n

can be viewed as a set of n distinct equations of the form Ax = b. These equations define the matrix X as the inverse of A. To be precise, let X_i denote the ith column of X, and recall that the unit vector e_i is the ith column of I_n. Equation (24) can then be solved for X by using the LUP decomposition for A to solve each equation

AX_i = e_i

separately for X_i. Each of the n X_i can be found in time (n²), and so the computation of X from the LUP decomposition of A takes time (n³). Since the LUP decomposition of A can be computed in time (n³), the inverse A^-1 of a matrix A can be determined in time (n³).

Matrix multiplication and matrix inversion

We now show that the theoretical speedups obtained for matrix multiplication translate to speedups for matrix inversion. In fact, we prove something stronger: matrix inversion is equivalent to matrix multiplication, in the following sense. If M(n) denotes the time to multiply two n n matrices and I(n) denotes the time to invert a nonsingular n n matrix, then I(n) = (M(n)). We prove this result in two parts. First, we show that M(n) = O(I(n)), which is relatively easy, and then we prove that I(n) = O(M(n)).

Theorem 11

If we can invert an n n matrix in time I(n), where I(n) = (n²) and I(n) satisfies the regularity condition I(3n) = O(I(n)), then we can multiply two n n matrices in time O(I(n)).

Proof Let A and B be n n matrices whose matrix product C we wish to compute. We define the 3n 3n matrix D by

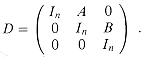
The inverse of D is

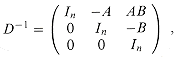
and thus we can compute the product AB by taking the upper right n n submatrix of D^-1.

We can construct matrix D in (n²) = O(I(n)) time, and we can invert D in O(I(3n)) = O(I(n)) time, by the regularity condition on I(n). We thus have

M(n) = O(I(n)).

Note that I(n) satisfies the regularity condition whenever I(n) does not have large jumps in value. For example, if I(n) = (n^c lg^d n) for any constants c > 0, d 0, then I(n) satisfies the regularity condition.

Reducing matrix inversion to matrix multiplication

The proof that matrix inversion is no harder than matrix multiplication relies on some properties of symmetric positive-definite matrices that will be proved in Section 6.

Theorem 12

If we can multiply two n n real matrices in time M(n), where M(n) = (n²) and M(n) = O(M(n + k)) for 0 k n, then we can compute the inverse of any real nonsingular n n matrix in time O(M(n)).

Proof We can assume that n is an exact power of 2, since we have

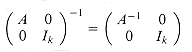
for any k > 0. Thus, by choosing k such that n + k is a power of 2, we enlarge the matrix to a size that is the next power of 2 and obtain the desired answer A^-1 from the answer to the enlarged problem. The regularity condition on M(n) ensures that this enlargement does not cause the running time to increase by more than a constant factor.

For the moment, let us assume that the n n matrix A is symmetric and positive-definite. We partition A into four n/2 n/2 submatrices:

Then, if we let

S = D - CB C^T

be the Schur complement of A with respect to B, we have

since AA^-1 = I_n, as can be verified by performing the matrix multiplication. The matrices B^-1 and S exist if A is symmetric and positive-definite, by Lemmas 13, 14, and 15 in Section 6, because both B and S are symmetric and positive-definite. By Exercise 1-3, B^-1C^T = (CB^-1)^T and B^-1C^TS = (S^-1 CB )^T. Equations (26) and (27) can therefore be used to specify a recursive algorithm involving 4 multiplications of n/2 n/2 matrices:

C B^-1,
(CB^-1) C^T,
S (CB^-1),
(CB^-1)^T (S^-1 CB^-1).

Since we can multiply n/2 n/2 matrices using an algorithm for n n matrices, matrix inversion of symmetric positive-definite matrices can be performed in time

I(n) 2I(n/2) + 4M(n) + O(n²)
= 2I(n/2) + O(M(n))
= O(M(n)).

It remains to prove that the asymptotic running time of matrix multiplication can be obtained for matrix inversion when A is invertible but not symmetric and positive-definite. The basic idea is that for any nonsingular matrix A, the matrix A^TA is symmetric (by Exercise 1-3) and positive-definite (by Theorem 6). The trick, then, is to reduce the problem of inverting A to the problem of inverting A^TA.

The reduction is based on the observation that when A is an n n nonsingular matrix, we have

A (A^TA)^-1A^T,

since ((A^TA)^-1 A^T)A = (A^TA)^-1(A^TA) = I_n and a matrix inverse is unique. Therefore, we can compute A^-1 by first multiplying A^T by A to obtain A^TA, then inverting the symmetric positive-definite matrix A^TA using the above divide-and-conquer algorithm, and finally multiplying the result by A^T. Each of these three steps takes O(M(n)) time, and thus any nonsingular matrix with real entries can be inverted in O(M(n)) time.

The proof of Theorem 12 suggests a means of solving the equation Ax = b without pivoting, so long as A is nonsingular. We multiply both sides of the equation by A^T, yielding (A^TA)x = A^Tb. This transformation doesn't affect the solution x, since A^T is invertible, so we can factor the symmetric positive-definite matrix A^TA by computing an LU decomposition. We then use forward and back substitution to solve for x with the right-hand side A^Tb. Although this method is theoretically correct, in practice the procedure LUP-DECOMPOSITION works much better. LUP decomposition requires fewer arithmetic operations by a constant factor, and it has somewhat better numerical properties.

Exercises

Let M(n) be the time to multiply n n matrices, and let S(n) denote the time required to square an n n matrix. Show that multiplying and squaring matrices have essentially the same difficulty: S(n) = (M(n)).

Let M(n) be the time to multiply n n matrices, and let L(n) be the time to compute the LUP decomposition of an n n matrix. Show that multiplying matrices and computing LUP decompositions of matrices have essentially the same difficulty: L(n) = (M(n)).

Let M(n) be the time to multiply n n matrices, and let D(n) denote the time required to find the determinant of an n n matrix. Show that finding the determinant is no harder than multiplying matrices: D(n) = O(M(n)).

Let M(n) be the time to multiply n n boolean matrices, and let T(n) be the time to find the transitive closure of n n boolean matrices. Show that M(n) = O(T(n)) and T(n) = O(M(n)lg n).

Does the matrix-inversion algorithm based on Theorem 12 work when matrix elements are drawn from the field of integers modulo 2? Explain.

Generalize the matrix-inversion algorithm of Theorem 12 to handle matrices of complex numbers, and prove that your generalization works correctly. (Hint: Instead of the transpose of A, use the conjugate transpose A*, which is obtained from the transpose of A by replacing every entry with its complex conjugate. Instead of symmetric matrices, consider Hermitian matrices, which are matrices A such that A = A*.)