| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
PREFACE 5
CHAPTER 1 7
Introduction 7
Zero-Point Energy Issues 7
Statement of the Problem 21
Purpose of the Study 24
Importance of the Study 24
Rationale of the Study 27
Definition of Terms 28
Overview of the Study 30
CHAPTER 2 32
Review of Related Literature 32
Historical Perspectives 32
Casimir Predicts a Measurable ZPE Effect 35
Ground State of Hydrogen is Sustained by ZPE 36
Lamb Shift Caused by ZPE 37
Experimental ZPE 38
ZPE Patent Review 40
ZPE and Sonoluminescence 43
Gravity and Inertia Related to ZPE 44
Heat from ZPE 45
Summary 46
CHAPTER 3 49
Methodology 49
Approach 49
What is a Feasibility Study? 50
Data Gathering Method 52
Database Selected for Analysis 52
Analysis of Data 53
Validity of Data 53
Uniqueness and Limitations of the Method 53
Summary 54
CHAPTER 4 55
Analysis 55
Introduction to Vacuum Engineering 55
Electromagnetic Energy Conversion 55
Microsphere Energy Collectors 65
Nanosphere Energy Scatterers 73
Picosphere Energy Resonators 77
Quantum Femtosphere Amplifiers 84
Deuteron Femtosphere 88
Electron Femtosphere 91
Casimir Force Electricity Generator 94
Cavity QED Controls Vacuum Fluctuations 100
Spatial Squeezing of the Vacuum 102
Focusing Vacuum Fluctuations 104
Stress Enhances Casimir Deflection 105
Casimir Force Geometry Design 107
Vibrating Cavity Photon Emission 113
Fluid Dynamics of the Quantum Vacuum 115
Quantum Coherence Accesses Single Heat Bath 120
Thermodynamic Brownian Motors 126
Transient Fluctuation Theorem 132
Power Conversion of Thermal Fluctuations 135
Rectifying Thermal Noise 137
Quantum Brownian Nonthermal Recifiers 142
Vacuum Field Amplification 146
CHAPTER 5 148
Summary, Conclusions and Recommendations 148
Summary 148
Electromagnetic Conversion 149
Mechanical Casimir Force Conversion 152
Fluid Dynamics 153
Thermodynamic Conversion 154
Conclusions 159
Recommendations 160
FIGURE CREDITS 163
REFERENCES 168
Today this country faces a destabilizing dependency on irreplaceable fossil fuels which are also rapidly dwindling. As shortages of oil and natural gas occur with more frequency, the New Energy Crisis is now heralded in the news media. However, an alternate source of energy that can replace fossil fuels has not been reliably demonstrated. A real need exists for a portable source of power that can compete with fossil fuel and its energy density. A further need exists on land, in the air, and in space, for a fuelless source of power which, by definition, does not require re-fueling. The future freedom, and quite possibly the future survival, of mankind depend on the utilization of such a source of energy, if it exists.
However, ubiquitous zero-point energy is known to exist. Yet, none of the worlds physicists or engineers are participating in any national or international energy development project beyond nuclear power. It is painfully obvious that zero-point energy does not appear to most scientists as the robust source of energy worth developing. Therefore, an aim of this study is to provide a clear understanding of the basic principles of the only known candidate for a limitless, fuelless source of power: zero-point energy. Another purpose is to look at the feasibility of various energy conversion methods that are realistically available to modern engineering, including emerging nanotechnology, for the possible use of zero-point energy.
To accomplish these proposed aims, a review of the literature is provided, which focuses on the major, scientific discoveries about the properties of zero-point energy and the quantum vacuum. Central to this approach is the discerning interpretation of primarily physics publications in the light of mechanical, nuclear, thermal, electronic and electrical engineering techniques. Applying an engineering analysis to the zero-point energy literature places more emphasis the practical potential for its energy conversion, especially in view of recent advances in nanotechnology.
With primary reference to the works of H. B. G. Casimir, Fabrizio Pinto, Frank Mead and Peter Milonni, key principles for the proposed extraction of energy for useful work are identified and analyzed. These principles fall into the thermodynamic, fluidic, mechanical, and electromagnetic areas of primary, forcelike quantities that apply to all energy systems. A search of zero-point energy literature reveals that these principles also apply to the quantum level. The most feasible modalities for the conversion of zero-point energy into useful work, such as the fluctuation-driven transport of an electron ratchet, the quantum Brownian nonthermal rectifiers, and the Photo-Carnot engine are also explored in more detail. Specific suggestions for further research in this area conclude this study with a section devoted to summary, conclusions and recommendations.
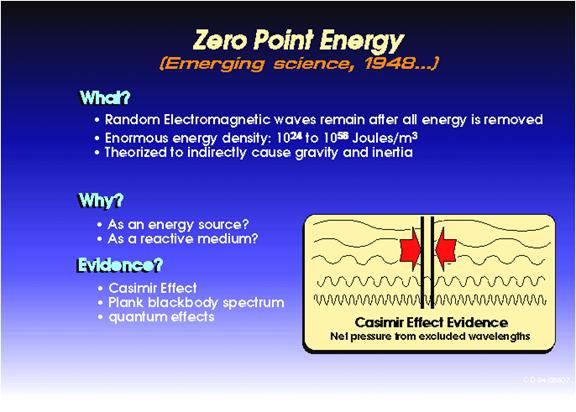
Zero-Point Energy Issues
Figure 1 NASA: www.grc.nasa.gov
Zero-point
energy (ZPE) is a universal natural phenomenon of great significance which has
evolved from the historical development of ideas about the vacuum. In the 17th century, it was thought that a
totally empty volume of space could be created by simply removing all
gases. This was the first generally
accepted concept of the vacuum. Late in
the 19th century, however, it became apparent that the evacuated region still
contained thermal radiation. To the natural philosophers of the day, it seemed
that all of the radiation might be
 eliminated by
cooling. Thus evolved the second concept
of achieving a real vacuum: cool it down to zero temperature after evacuation.
Absolute zero temperature (-273C) was far removed from the technical
possibilities of that century, so it seemed as if the problem was solved. In
the 20th century, both theory and experiment have shown that there
is a non-thermal radiation in the vacuum that persists even if the
temperature could be lowered to absolute zero. This classical concept alone explains the name of 'zero-point'
radiation .
eliminated by
cooling. Thus evolved the second concept
of achieving a real vacuum: cool it down to zero temperature after evacuation.
Absolute zero temperature (-273C) was far removed from the technical
possibilities of that century, so it seemed as if the problem was solved. In
the 20th century, both theory and experiment have shown that there
is a non-thermal radiation in the vacuum that persists even if the
temperature could be lowered to absolute zero. This classical concept alone explains the name of 'zero-point'
radiation .
In 1891, the worlds greatest electrical futurist, Nikola Tesla, stated, Throughout space there is energy. Is this energy static or kinetic? If static our hopes are in vain; if kinetic and we know it is, for certain then it is a mere question of time when men will succeed in attaching their machinery to the very wheelwork of Nature. Many generations may pass, but in time our machinery will be driven by a power obtainable at any point in the Universe.
From the papers studied the author has grown increasingly convinced as to the relevance of the ZPE in modern physics. The subject is presently being tackled with appreciable enthusiasm and it appears that there is little disagreement that the vacuum could ultimately be harnessed as an energy source. Indeed, the ability of science to provide ever more complex and subtle methods of harnessing unseen energies has a formidable reputation. Who would have ever predicted atomic energy a century ago?
A good experiment proving the existence of ZPE is accomplished by cooling helium to within microdegrees of absolute zero temperature. It will still remain a liquid. Only ZPE can account for the source of energy that is preventing helium from freezing.
Besides the classical explanation of zero-point energy referred to above, there are rigorous derivations from quantum physics that prove its existence. It is possible to get a fair estimate of the zero point energy using the uncertainty principle alone. As stated in Equation (1), Plancks constant h (6.63 x 10-34 joule-sec) offers physicists the fundamental size of the quantum. It is also the primary ingredient for the uncertainty principle. One form is found in the minimum uncertainty of position x and momentum p expressed as
Δx Δp > h/4p . (1)
Figure 2
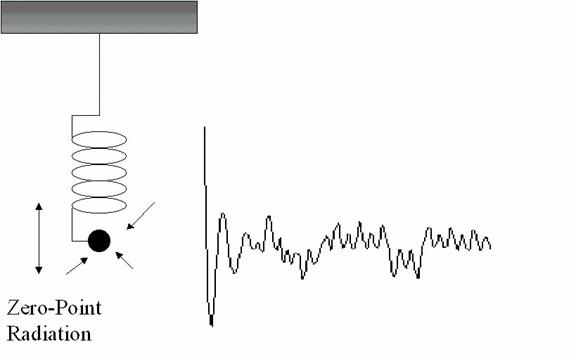
In quantum mechanics, Plancks constant also is present in the description of
particle motion. The harmonic oscillator reveals the effects of zero-point
radiation on matter. The oscillator consists of an electron attached to an
ideal, frictionless spring. When the electron is set in motion, it oscillates
about its point of equilibrium, emitting electromagnetic radiation at the
frequency of oscillation. The radiation dissipates energy, and so in the
absence of zero-point radiation and at a temperature of absolute zero the
electron eventually comes to rest. Actually, zero-point radiation continually
imparts random impulses to the electron, so that it never comes to a complete
stop [as seen in Figure 2]. Zero-point radiation gives the oscillator an
average energy equal to the frequency of oscillation multiplied by one-half of
Planck's constant.
However, a question regarding the zero-point field (ZPF) of the vacuum can be asked, such as, What is oscillating and how big is it? To answer this, a background investigation needs to be done. The derivation which follows uses well-known physics parameters. It serves to present a conceptual framework for the quantum vacuum and establish a basis for the extraordinary nature of ZPE.
In quantum electrodynamics (QED), the fundamental size of the quantum is also reflected in the parton size. In 1969 Feynman proposed the parton model of the nucleon, which is reminiscent of a model of the electron which was extant in the late 19th and early 20th centuries: The nucleon was assumed to consist of extremely small particlesthe partonswhich fill the entire space within a nucleon. All the constituents of a nucleon are identical, as are their electric charges. This is the simplest parton model.
The derivation of the parton mass gives us a theoretical idea of how small the structure of the quantum vacuum may be and, utilizing E = mc2, how large ZPE density may be. For convenience, we substitute h = hbar = h/2p for which the average ZPE = ½ hf = ½ hω, since the angular frequency ω = 2pf.
The Abraham-Lorentz radiation reaction equation contains the relevant quantity, since the radiation damping constant G for a particles self-reaction is intimately connected to the fluctuations of the vacuum. The damping constant is
G = B e2 / moc3 (2)
where mo is the particle mass. It is also known in stochastic electrodynamics (SED) that the radiation damping constant can be found from the ZPE-determined inertial mass associated with the parton oscillator. It is written as
G = p mo c2 / hωc2 (3)
Here ωc is the zero-point cut-off frequency which is regarded to be on the order of the Planck cut-off frequency (see eq. 8), given by
![]() ωc = p c5
/ hG (4)
ωc = p c5
/ hG (4)
Equating (2) and (3), substituting Equation (4) and rearranging for mo gives
![]() mo = e B
/ G
(5)
mo = e B
/ G
(5)
Therefore, the parton mass is calculated to be
mo 0.16 kg . (6)
For comparison, the proton rest mass is approximately 10-27 kg, with a mass density of 1014 g/cc. Though it might be suggested that quarks play the role of partons the quark rest mass is known to be much smaller than loosely bound protons or electrons. Therefore, Equation (6) suggests that partons are fundamentally different.
The answer to the question of how big is the oscillatory particle in the ZPF quantum vacuum comes from QED. The length at which quantum fluctuations are believed to dominate the geometry of space-time is the Planck length:
![]() Planck length = Gh/2pc3 10-35 m (7)
Planck length = Gh/2pc3 10-35 m (7)
The Planck length is therefore useful as a measure of the approximate size of a parton, as well as a spatial periodicity characteristic of the Planck cutoff frequency. Since resonant wavelength is classically determined by length or particle diameter, we can use the Planck length as the wavelength l in the standard equation relating wavelength and frequency,
c = f l = ωc l /2p (8)
and solving for ωc to find the Planck cutoff frequency ωc 1043 Hz. This value sets an upper limit on design parameters for ZPE conversion, as reviewed in the later chapters. Taking Equation (6) divided by Equation (7), the extraordinary ZPF mass density estimate of 10101 g/cc seems astonishing, though, like positrons (anti-electrons), the ZPF consists mostly of particles in negative energy states. This derived density also compares favorably with other estimates in the literature: Robert Forward calculates 1094 g/cc if ZPE was limited to particles of slightly larger size, with a ZPF energy density of 10108 J/cc. (NASA has a much smaller but still enormous estimate revealed in Figure 1.)
Another area of concern to the origin of the theoretical derivation of ZPE is a rudimentary understanding of what meaning Planck attributed to the average value of an elementary radiator. The absorption of radiation was assumed to proceed according to classical theory, whereas emission of radiation occurred discontinuously in discrete quanta of energy. Plancks second theory, published in 1912, was the first prediction of zero-point energy. Following Boltzmann, Planck looked at a distribution of harmonic oscillators as a composite model of the quantum vacuum. From thermodynamics, the partial differential of entropy with respect to potential energy is ∂S/∂U = 1/T. Max Planck used this to obtain the average energy of the radiators as
U = ½hf + hf /(e hf/ kT 1) (9)
where here the ZPE term ½hf is added to the radiation law term of his first theory. Using this equation, which marked the birth of the concept of zero-point energy, it is clear that as absolute temperature T à 0 then U à ½hf, which is the average ZPE
Interestingly, the ground state energy of a simple harmonic oscillator (SHO) model can also be used to find the average value for zero-point energy. This is a valuable exercise to show the fundamental basis for zero-point energy parton oscillators. The harmonic oscillator is used as the model for a particle with mass m in a central field (the spring in Figure 2). The uncertainty principle provides the only requisite for a derivation of the minimum energy of the simple harmonic oscillator, utilizing the equation for kinetic and potential energy,
E = p2/2m + ½ m ω2 x2 . (10)
Solving the uncertainty relation from Equation (1) for p, one can substitute it into Equation (10). Using a calculus approach, one can take the derivative with respect to x and set the result equal to zero. A solution emerges for the value of x that is at the minimum energy E for the SHO. This x value can then be placed into the minimum energy SHO equation where the potential energy is set equal to the kinetic energy. The ZPE solution yields ½hf for the minimum energy E.
This simple derivation reveals the profoundly fundamental effect of zero-point radiation on matter, even when the model in only a SHO. The oscillator consists of a particle attached to an ideal, frictionless spring. When the parton is in motion, it accelerates as it oscillates about its point of equilibrium, emitting radiation at the frequency of oscillations. The radiation dissipates energy and so in the absence of zero-point radiation and at a temperature of absolute zero the particle would eventually comes to rest. In actuality, zero-point radiation continually imparts random impulses to the particle so that it never comes to rest. This is Zitterbewegung motion. The consequence of this Zitterbewegung is the averaged energy of Equation (15) imparted to the particle, which has an associated long-range, van der Waals, radiation field which can even be identified with Newtonian gravity. Information on this discovery is reviewed in Chapter 2.
In QED, the employment of perturbation techniques amounts to treating the interaction between the electron and photon (between the electron-positron field and the electromagnetic field) as a small perturbation to the collection of the free fields. In the higher order calculations of the resulting perturbative expansion of the S-matrix (Scattering matrix), divergent or infinite integrals are encountered, which involve intermediate states of arbitrarily high energies. In standard QED, these divergencies are circumvented by redefining or renormalizing the charge and the mass of the electron. By the renormalization procedure, all reference to the divergencies are absorbed into a set of infinite bare quantities. Although this procedure has made possible some of the most precise comparisons between theory and experiment (such as the g - 2 determinations) its logical consistency and mathematical justification remain a subject for controversies. Therefore, it is valuable to briefly review how the renormalization process is related to the ZPE vacuum concept in QED.
The vacuum is defined as the ground state or the lowest energy state of the fields. This means that the QED vacuum is the state where there are no photons and no electrons or positrons. However, as we shall see in the next section, since the fields are represented by quantum mechanical operators, they do not vanish in the vacuum state but rather fluctuate. The representation of the fields by operators also leads to a vacuum energy (sometimes referred to as vacuum zero-point energy).
When interactions between the electromagnetic and the electron-positron field in the vacuum are taken into account, which amounts to consider higher order contributions to the S-matrix, the fluctuations in the energy of the fields lead to the formation of so-called virtual electron-positron pairs (since the field operators are capable of changing the number of field quanta (particles) in a system). It is the evaluation of contributions like these to the S-matrix that lead to the divergencies mentioned above and prompt the need for renormalization in standard QED.
The vacuum state contains no stable particles. The vacuum in QED is believed to be the scene of wild activity with zero-point energy and particles/anti-particles pairs constantly popping out of the vacuum only to annihilate again immediately afterwards. This affects charged particles with oppositely charged virtual particles and is referred to as vacuum polarization. Since the 1930's, for example, theorists have proposed that virtual particles cloak the electron, in effect reducing the charge and electromagnetic force observed at a distance.
Figure 3![]()
 Vacuum polarization is, however, a
relativistic effect involving electron-positron pairs, as the hole-theoretic
interpretation assumes: an electrostatic field causes a redistribution of
charge in the Dirac sea and thus polarizes the vacuum. A single
Vacuum polarization is, however, a
relativistic effect involving electron-positron pairs, as the hole-theoretic
interpretation assumes: an electrostatic field causes a redistribution of
charge in the Dirac sea and thus polarizes the vacuum. A single
charged particle, in particular, will polarize the
vacuum near it, so that its observed charge is actually smaller than its bare
charge. A proton, for instance, will attract electrons and repel positrons of
the Dirac sea, resulting in a partial screening of its bare charge and a
modification of the Coulomb potential in the hydrogen atom.
Even an atom, for instance, can be considered to be dressed by emission and
reabsorption of virtual photons from the vacuum.
This constant virtual particle flux of the ZPE is especially noticeable near
the boundaries of bigger particles, because the intense electric field gradient
causes a more prodigious decay of the vacuum.
In a notable experiment designed to penetrate the virtual particle cloud surrounding the electron, Koltick used a particle accelerator at energies of 58 GeV (gigaelectronvolts) without creating other particles. From his data, a new value of the fine structure constant was obtained (e2/hc = 1/128.5), while a smaller value of 1/137 is traditionally observed for a fully screened electron. This necessarily means that the value for a naked electron charge is actually larger than textbooks quote for a screened electron.
Often regarded as merely an artifact of a sophisticated mathematical theory, some experimental verification of these features of the vacuum has already been obtained, such as with the Casimir pressure effect (see Figure 6). An important reason for investigating the Casimir effect is its manifestation before interactions between the electromagnetic field and the electron/positron fields are taken into consideration. In the language of QED, this means that the Casimir effect appears already in the zeroth order of the perturbative expansion. In this sense the Casimir effect is the most evident feature of the vacuum. On the experimental side, the Casimir effect has been tested very accurately.
Some argue that there are two ways of looking at the Casimir effect:
1) The boundary plates modify an already existing QED vacuum. That is, the introduction of the boundaries (e.g. two electrically neutral, parallel plates) modify something (a medium of vacuum zero-point energy/vacuum fluctuations) which already existed prior to the introduction of the boundaries.
2) The effect is due to interactions between the microscopic constituents in the boundary plates. That is, the boundaries introduce a source which give rise to the effect. The atomic or molecular constituents in the boundary plates act as fluctuating sources that generate the interactions between the constituents. The macroscopic attractive force between the two plates arises as an integrated effect of the mutual interactions between the many microscopic constituents in these boundary plates.
The second view is based on atoms within the boundary plates with fluctuating dipole moments that normally give rise to van der Waals forces. Therefore, the first view, I believe, is the more modern version, acknowledging the transformative effect of the introduction of the Dirac sea on modern QED and its present view of the vacuum.
To conclude this introductory ZPE issues section, it is essential to review the fluctuation-dissipation theorem, which is prominently featured in QED, forming the basis for the treatment of an oscillating particle in equilibrium with the vacuum. It was originally presented in a seminal paper by Callen et al. based on systems theory, offering applications to various systems including Brownian motion and also electric field fluctuations in a vacuum. In this theorem, the vacuum is treated as a bath coupled to a dissipative force.
Generally speaking, if a system is coupled to a bath that can take energy from the system in an effectively irreversible way, then the bath must also cause fluctuations. The fluctuations and the dissipation go hand in hand; we cannot have one without the otherthe coupling of a dipole oscillator to the electromagnetic field has a dissipative component, in the form of radiation reaction, and a fluctuation component, in the form of zero-point (vacuum) field; given the existence of radiation reaction, the vacuum field must also exist in order to preserve the canonical commutation rule and all it entails.
The fluctuation-dissipation theorem is a generalized Nyquist relation. It establishes a relation between the impedance in a general linear dissipative system and the fluctuations of appropriate generalized forces.
![]() The
theorem itself is expressed as a single equation, essentially the same as the
original formula by Johnson from Bell Telephone Laboratory who, using kBT
with equipartition, discovered the thermal agitation noise of electricity,
The
theorem itself is expressed as a single equation, essentially the same as the
original formula by Johnson from Bell Telephone Laboratory who, using kBT
with equipartition, discovered the thermal agitation noise of electricity,
< V2 > = 2/p R(ω) E(ω,T) dω . (11)
Here < V2 > is the root mean square (RMS) value of the spontaneously fluctuating force, R(ω) is the generalized impedance of the system and E(ω,T) is the mean energy at temperature T of an oscillator of natural frequency ω,
E (ω,T) = ½ hω
+ hω/(e
hω/kT
1) (12)
which is the same Planck law as Equation (9). The use of the theorems Equation (11) applies exclusively to systems that have an irreversible linear dissipative portion, such as an impedance, capable of absorbing energy when subjected to a time-periodic perturbation. This is an essential factor to understanding the theorems applicability.
The system may be said to be linear if the power dissipation is quadratic in the magnitude of the perturbation. If the condition of irreversibility is satisfied, such as with resistive heating, then the theorem predicts that there must exist a spontaneously fluctuating force coupled to it in equilibrium. This constitutes an insight into the function of the quantum vacuum in a rigorous and profound manner. The existence of a radiation impedance for the electromagnetic radiation from an oscillating charge is shown to imply a fluctuating electric field in the vacuum, and application of the general theorem yields the Planck radiation law.
Applying the theorem to ZPE, Callen et al. use radiation reaction as the dissipative force for electric dipole radiation of an oscillating charge in the vacuum. Based on Equation (2), we can express this in terms of the radiation damping constant and the change in acceleration (2nd derivative of velocity),
Fd = (B e2/c3) 2v/ t2 = G m 2v/ t2 (13)
which is also the same equation derived by Feynman with a subtraction of retarded and advanced fields, followed by a reduction of the particle radius à 0 for the radiation resistance force Fd. Then, the familiar equation of motion for the accelerated charge with an applied force F and a natural frequency ωo is
F = m v/ t + m ωo2 x + Fd . (14)
For an oscillating dipole and dissipative Equation (13), Callen et al. derive the real part of the impedance from the ratio of the in-phase component of F to v, which can also be expressed in terms of the radiation damping constant
R(ω) = B ω2e2/c3 = G m ω2 (15)
which is placed, along with Equation (12), into Equation (11). This causes < V2 > to yield the same value as the energy density for isotropic radiation. Interestingly, V must then be a randomly fluctuating force eE on the charge with the conclusion regarding the ZPF, hence a randomly fluctuating electric field E.
This intrinsically demonstrates the vital relationship between the vacuum fluctuation force and an irreversible, dissipative process. The two form a complimentary relationship, analogous to Equation (1), having great fundamental significance.
Statement of the Problem
The engineering challenge of converting or extracting zero-point energy for useful work is, at the turn of this century, plagued by ignorance, prejudice and disbelief. The physics community does not in general acknowledge the emerging opportunities from fundamental discoveries of zero-point energy. Instead, there are many expositions from prominent sources explaining why the use of ZPE is forbidden.
A scientific editorial opinion states, Exactly how much zero-point energy resides in the vacuum is unknown. Some cosmologists have speculated that at the beginning of the universe, when conditions everywhere were more like those inside a black hole, vacuum energy was high and may have even triggered the big bang. Today the energy level should be lower. But to a few optimists, a rich supply still awaits if only we knew how to tap into it. These maverick proponents have postulated that the zero-point energy could explain cold fusion, inertia, and other phenomena and might someday serve as part of a negative mass system for propelling spacecraft. In an interview taped for PBSs Scientific American Frontiers, which aired in November (1997), Harold E. Puthoff, the director of the Institute for Advanced Studies, observed: For the chauvinists in the field like ourselves, we think the 21st century could be the zero-point-energy age. That conceit is not shared by the majority of physicist; some even regard such optimism as pseudoscience that could leech funds from legitimate research. The conventional view is that the energy in the vacuum is miniscule.
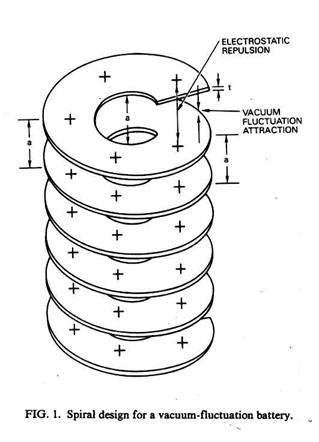
Dr. Robert Forward, who passed away in 2002, said, Before I wrote the paper everyone said that it was impossible to extract energy from the vacuum. After I wrote the paper, everyone had to acknowledge that you could extract energy from the vacuum, but began to quibble about the details. The spiral design won't work very efficiently The amount of energy extracted is extremely small You are really getting the energy from the surface energy of the aluminum, not the vacuum Even if it worked perfectly, it would be no better per pound than a regular battery Energy extraction from the vacuum is a conservative process, you have to put as much energy into making the leaves of aluminum as you will ever get out of the battery etc etcYes, it is very likely that the vacuum field is a conservative one, like gravity. But, no one has proved it yet. In fact, there is an experiment mentioned in my Mass Modification [ref. 15] paper (an antiproton in a vacuum chamber) which can check on that. The amount of energy you can get out of my aluminum foil battery is limited to the total surface energy of all the foils. For foils that one can think of making that are thick enough to reflect ultraviolet light, so the Casimir attraction effect works, say 20 nm (70 atoms) thick, then the maximum amount of energy you get out per pound of aluminum is considerably less than that of a battery. To get up to chemical energies, you will have to accrete individual atoms using the van der Waals force, which is the Casimir force for single atoms instead of conducting plates. My advice is to accept the fact that the vacuum field is probably conservative, and invent the vacuum equivalent of the hydroturbine generator in a dam.
Professor
John Barrow from
With convincing skeptical arguments like these from the experts, how can the extraction of ZPE for the performance of useful work ever be considered feasible? What engineering protocol can be theoretically developed for the extraction of ZPE if it can be reasonably considered to be feasible? These are the central problems that are addressed by my thesis.
Purpose of the Study
This study is designed to propose a defensible feasibility argument for the extraction of ZPE from the quantum vacuum. Part of this comprehensive feasibility study also includes an engineering analysis of areas of research that are proving to be fruitful in the theoretical and experimental approaches to zero-point energy extraction. A further purpose is to look at energy extraction systems, in their various modalities, based on accepted physics and engineering principles, which may provide theoretically fruitful areas of discovery. Lastly, a few alternate designs which are reasonable prototypes for the extraction of zero-point energy, are also proposed.
Importance of the Study
It is unduly apparent that a study of this
ubiquitous energy is overdue. The question has been asked, Can new technology
reduce our need for oil from the
In 1956, the geologist M. King Hubbert predicted
that
Figure 4
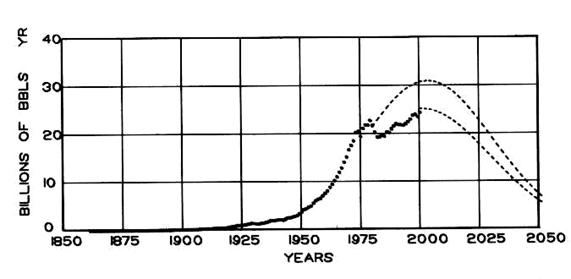
It is now widely accepted, especially in Europe where I participated in the
World Renewable Energy Policy and Strategy Forum, Solar Energy Expo 2002 and
the Innovative Energy Technology Conference, (all in
Another emerging
problem that seems to have been unanticipated by the environmental groups is
that too much proliferation of one type of machinery, such as windmills, can be
objectionable as well. Recently, the
Dr. Steven Greer of the Disclosure Project has stated, classified above top-secret projects possess fully operational anti-gravity propulsion devices and new energy generation systems, that, if declassified and put to peaceful uses, would empower a new human civilization without want, poverty or environmental damage. However, since the declassification of black project, compartmented exotic energy technologies is not readily forthcoming, civilian physics research is being forced to reinvent fuelless energy sources such as zero-point energy extraction.
Regarding the existing conundrum of interplanetary travel, with our present lack of appropriate propulsion technology and cosmic ray bombardment protection, Arthur C. Clarke has predicted, that in 3001 the inertialess drive will most likely be put to use like a controllable gravity field, thanks to the landmark paper by Haisch et al. if HR&Ps theory can be proved, it opens up the prospecthowever remoteof antigravity space drives, and the even more fantastic possibility of controlling inertia.
Rationale of the Study
The hypothesis of the study is centered on the accepted physical basis for zero-point energy, its unsurpassed energy density, and the known physical manifestations of zero-point energy, proven by experimental observation. Conversion of energy is a well-known science which can, in theory, be applied to zero-point energy.
The scope of the study encompasses the known areas of physical discipline: mechanical, thermal, fluidic, and electromagnetic. Within these disciplines, the scope also extends from the macroscopic beyond the microscopic to the atomic. This systems science approach, which is fully discussed and analyzed in Chapter 4, includes categories such as:
Electromagnetic conversion of zero-point energy radiation
Fluidic entrainment of zero-point energy flow through a gradient
Mechanical conversion of zero-point energy force or pressure
Thermodynamic conversion of zero-point energy.
Definition of Terms
Following are terms that are used throughout the study:
Bremsstrahlung: Radiation caused by the deceleration of an electron. Its energy is converted into light. For heavier particles the retardations are never so great as to make the radiation important.
Energy: The capacity for doing work. Equal to power exerted over time (e.g. kilowatt-hours). It can exist in linear or rotational form and is quantized in the ultimate part. It may be conserved or not conserved, depending upon the system considered. Mostly all terrestrial manifestations can be traced to solar origin, except for zero-point energy.
Lamb Shift: A shift (increase) in the energy levels of an atom, regarded as a Stark effect, due to the presence of the zero-point field. Its explanation marked the beginning of modern quantum electrodynamics.
Parton: The fundamental theoretical limit of particle size thought to exist in the vacuum, related to the Planck length (10-35 meter) and the Planck mass (22 micrograms), where quantum effects dominate spacetime. Much smaller than subatomic particles, it is sometimes referred to as the charged point particles within the vacuum that participate in the ZPE Zitterbewegung.
Plancks Constant: The fundamental basis of quantum mechanics which provides the measure of a quantum (h = 6.6 x 10-34 joule-second), it is also the ratio of the energy to the frequency of a photon.
Quantum Electrodynamics: The quantum theory of light as electromagnetic radiation, in wave and particle form, as it interacts with matter. Abbreviated QED.
Quantum Vacuum: A characterization of empty space by which physical particles are unmanifested or stored in negative energy states. Also called the physical vacuum.
Uncertainty Principle: The rule or law that limits the precision of a pair of physical measurements in complimentary fashion, e.g. the position and momentum, or the energy and time, forming the basis for zero-point energy.
Virtual Particles: Physically real particles emerging from the quantum vacuum for a short time determined by the uncertainty principle. This can be a photon or other particle in an intermediate state which, in quantum mechanics (Heisenberg notation) appears in matrix elements connecting initial and final states. Energy is not conserved in the transition to or from the intermediate state. Also known as a virtual quantum.
Zero-point energy: The non-thermal, ubiquitous kinetic energy (averaging ½hf) that is manifested even at zero degrees Kelvin, abbreviated as ZPE. Also called vacuum fluctuations, zero-point vibration, residual energy, quantum oscillations, the vacuum electromagnetic field, virtual particle flux, and recently, dark energy.
Zitterbewegung: An oscillatory motion of an electron, exhibited mainly when it penetrates a voltage potential, with frequency greater than 1021 Hertz. It can be associated with pair production (electron-positron) when the energy of the potential exceeds 2mc2 (m = electron mass). Also generalized to represent the rapid oscillations associated with zero-point energy.
Overview of the Study
In all of the areas of investigation, so far no known extractions of zero-point energy for useful work have been achieved, though it can be argued that incidental ZPE extraction has manifested itself macroscopically. By exploring the main physical principles underlying the science of zero-point energy, certain modalities for energy conversion achieve prominence while others are regarded as less practical. Applying physics and engineering analysis, a scientific research feasibility study of ZPE extraction, referenced by rigorous physics theory and experiment is generated.
With a comprehensive survey of conversion modalities, new alternate, efficient methods for ZPE extraction are presented and analyzed. Comparing the specific characteristics of zero-point energy with the known methods of energy conversion, the common denominators should offer the most promising feasibility for conversion of zero-point energy into useful work. The advances in nanotechnology are also examined, especially where ZPE effects are already identified as interfering with mechanical and electronic behavior of nanodevices.
Historical Perspectives
Reviewing the literature for zero-point energy necessarily starts with the historical developments of its discovery. In 1912, Max Planck published the first journal article to describe the discontinuous emission of radiation, based on the discrete quanta of energy. In this paper, Plancks now-famous blackbody radiation equation contains the residual energy factor, one half of hf, as an additional term (½hf), dependent on the frequency f, which is always greater than zero (where h = Plancks constant). It is therefore widely agreed that Plancks equation marked the birth of the concept of zero-point energy. This mysterious factor was understood to signify the average oscillator energy available to each field mode even when the temperature reaches absolute zero. In the meantime, Einstein had published his fluctuation formula which describes the energy fluctuations of thermal radiation. Today, the particle term in the Einstein fluctuation formula may be regarded as a consequence of zero-point field energy.
During the early years of its discovery, Einstein , and Dirac , saw the value of zero-point energy and promoted its fundamental importance. The 1913 paper by Einstein computed the specific heat of molecular hydrogen, including zero-point energy, which agreed very well with experiment. Debye also made calculations including zero-point energy (ZPE) and showed its effect on Roentgen ray (X-ray) diffraction.
Throughout the next few decades, zero-point energy became intrinsically important to quantum mechanics with the birth of the uncertainty principle. In 1927, Heisenberg, on the basis of the Einstein-de Broglie relations, showed that it is impossible to have a simultaneous knowledge of the [position] coordinate x and its conjugate momentum p to an arbitrary degree of accuracy, their uncertainties being given by the relation Δx Δp > h / 4p. This expression of Equation (1) is not the standard form that Heisenberg used for the uncertainty principle, however. He invented a character h called h-bar, which equals h/2p (also introduced in Chapter 1). If this shortcut notation is used for the uncertainty principle, it takes the form Δx Δp > h / 2 or ΔE Δt > h / 2, which is a more familiar equation to physicists and found in most quantum mechanics texts.
By 1935, the application of harmonic oscillator models with various boundary conditions became a primary approach to quantum particle physics and atomic physics. Quantum mechanics also evolved into wave mechanics and matrix mechanics which are not central to this study. However, with the evolution of matrix mechanics came an intriguing application of matrix operators and commutation relations of x and p that today are well known in quantum mechanics. With these new tools, the quantization of the harmonic oscillator is all that is required to reveal the existence of the zero-point ground state energy.
This residual energy is known as the zero-point energy, and is a direct consequence of the uncertainty principle. Basically, it is impossible to completely stop the motion of the oscillator, since if the motion were zero, the uncertainty in position Δx would be zero, resulting in an infinitely large uncertainty in momentum (since Δp = h / 2Δx). The zero-point energy represents a sharing of the uncertainty in position and the uncertainty in momentum. The energy associated with the uncertainty in momentum gives the zero-point energy.
Another important ingredient in the development of the understanding of zero-point energy came from the Compton effect. Compelling confirmation of the concept of the photon as a concentrated bundle of energy was provided in 1923 by A. H. Compton who earned a Nobel prize for this work in 1927. Compton scattering, as it is now known, can only be understood using the energy-frequency relation E = hf that was proposed previously by Einstein to explain the photoelectric effect in terms of Plancks constant h.
Figure 5

Ruminations about the zero-point vacuum
field (ZPF), in conjunction with Einsteins famous equation E = mc2
and the limitations of the uncertainty principle, suggested that photons may
also be created and destroyed out of nothing. Such photons have been called
virtual and are prohibited by classical laws of physics. But in quantum
mechanics the uncertainty principle allows energy conservation to be violated
for a short time interval Δt = h / 2ΔE. As long as the
energy is conserved after this time, we can regard the virtual particle
exchange as a small fluctuation of energy that is entirely consistent with
quantum mechanics.
Such virtual particle exchanges later became an integral part of an advanced
theory called quantum electrodynamics (QED) where Feynmann diagrams,
developed by Richard Feynmann to describe particle collisions, often show the
virtual photon exchange between the paths of two nearby particles. Figure 5 shows a sample of the
Casimir Predicts a Measurable ZPE Effect
In 1948, it was predicted that virtual particle appearances should exert a force that is measurable. Casimir not only predicted the presence of such a force but also explained why van der Waals forces dropped off unexpectedly at long range separation between atoms. The Casimir effect was first verified experimentally using a variety of conductive plates by Sparnaay.
There was still an interest for an improved test of the Casimir force using conductive plates as modeled in Casimir's paper to better accuracy than Sparnaay. In 1997, Dr. Lamoreaux, from Los Alamos Labs, performed the experiment with less than one micrometer (micron) spacing between gold-plated parallel plates attached to a torsion pendulum. In retrospect, he found it to one of the most intellectually satisfying experiments that he ever performed since the results matched the theory so closely (within 5%). This event also elevated zero-point energy fluctuations to a higher level of public interest. Even the New York Times covered the event.
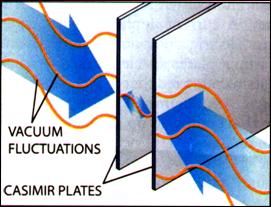 The
Casimir Effect has been posited as a force produced solely by activity in the
empty vacuum (see Figure 6). The Casimir force is also very powerful at small
distances. Besides being independent of temperature, it is inversely
proportional to the fourth power of the distance between the plates at larger
distances and inversely proportional to the third power of the distance between
the plates at short distances.
(Its frequency dependence is a third power.)
The
Casimir Effect has been posited as a force produced solely by activity in the
empty vacuum (see Figure 6). The Casimir force is also very powerful at small
distances. Besides being independent of temperature, it is inversely
proportional to the fourth power of the distance between the plates at larger
distances and inversely proportional to the third power of the distance between
the plates at short distances.
(Its frequency dependence is a third power.)
Figure 6
Lamoreaux's results come as no surprise to anyone familiar
with quantum electrodynamics, but they serve as a material confirmation of a
bazaar theoretical prediction: that QED predicts the all-pervading vacuum
continuously spawns particles and waves that spontaneously pop in and out of
existence. Their time of existence is strictly limited by the uncertainty principle
but they create some havoc while they bounce around during their brief
lifespan. The churning quantum foam is believed to extend throughout the
universe even filling the empty space within the atoms in human bodies.
Physicists theorize that on an infinitesimally small scale, far, far smaller
than the diameter of atomic nucleus, quantum fluctuations produce a foam of
erupting and collapsing, virtual particles, visualized as a topographic
distortion of the fabric of space time (Figure 7).
Ground State of Hydrogen is Sustained by ZPE
Figure 7 Figure 7
Looking at
the electron in a set ground-state orbit, it consists of a bound state with a
central Coulomb potential that has been treated successfully in
 physics with the harmonic oscillator model.
However, the anomalous repulsive force balancing the attractive Coulomb
potential remained a mystery until Puthoff published a ZPE-based description of
the hydrogen ground state.
physics with the harmonic oscillator model.
However, the anomalous repulsive force balancing the attractive Coulomb
potential remained a mystery until Puthoff published a ZPE-based description of
the hydrogen ground state.
This derivation caused a stir among physicists because of the
extent of influence that was now afforded to vacuum fluctuations. It appears
from Puthoffs work that the ZPE shield of virtual particles surrounding the
electron may be the repulsive force. Taking a simplistic argument for the rate
at which the atom absorbs energy from the vacuum field and equating it to the
radiated loss of energy from accelerated charges, the Bohr quantization
condition for the ground state of a one-electon atom like hydrogen is
obtained. We now know that the vacuum
field is in fact formally necessary for the stability of atoms in quantum
theory.
Lamb Shift Caused by ZPE
Another historically valid test in the verification of ZPE has been what has been called the Lamb shift. Measured by Dr. Willis Lamb in the 1940's, it actually showed the effect of zero point fluctuations on certain electron levels of the hydrogen atom, causing a fine splitting of the levels on the order of 1000 MHz. Physicist Margaret Hawton describes the Lamb shift as a kind of one atom Casimir Effect and predicts that the vacuum fluctuations of ZPE need only occur in the vicinity of atoms or atomic particles. This seems to agree with the discussion about Koltick in Chapter 1, illustrated in Figure 3.
 Today, the majority of physicists attribute
spontaneous emission and the Lamb shift entirely to vacuum fluctuations.
This may lead scientists to believe that it can no longer be called
'spontaneous emission' but instead should properly be labeled forced
or 'stimulated emission' much like laser light, even though there is
a random quality to it. However, it has been found that radiation reaction (the
reaction of the electron to its own field) together with the vacuum
fluctuations contribute equally to the phenomena of spontaneous emission.
Today, the majority of physicists attribute
spontaneous emission and the Lamb shift entirely to vacuum fluctuations.
This may lead scientists to believe that it can no longer be called
'spontaneous emission' but instead should properly be labeled forced
or 'stimulated emission' much like laser light, even though there is
a random quality to it. However, it has been found that radiation reaction (the
reaction of the electron to its own field) together with the vacuum
fluctuations contribute equally to the phenomena of spontaneous emission.
Experimental ZPE
Figure 8
Another interesting experiment is the 'Casimir Effect at Macroscopic Distances' which proposes observing the Casimir force at a distance of a few centimeters using confocal optical resonators within the sensitivity of laboratory instruments. This experiment makes the microscopic Casimir effect observable and greatly enhanced.
In general, many of the experimental journal articles refer to vacuum effects on a cavity that is created with two or more surfaces. Cavity QED is a science unto itself. Small cavities suppress atomic transitions; slightly larger ones, however, can enhance them. When the size of the cavity surrounding an excited atom is increased to the point where it matches the wavelength of the photon that the atom would naturally emit, vacuum-field fluctuations at that wavelength flood the cavity and become stronger than they would be in free space. It is also possible to perform the opposite feat. Pressing zero-point energy out of a spatial region can be used to temporarily increase the Casimir force. The materials used for the cavity walls are also important. It is well-known that the attractive Casimir force is obtained from highly reflective surfaces. However, a repulsive Casimir force may be obtained by considering a cavity built with a dielectric and a magnetic plate. The product r of the two reflection amplitudes is indeed negative in this case, so that the force is repulsive. For parallel plates in general, a magnetic field inhibits the Casimir effect.
An example of an idealized system with two parallel semiconducting plates separated by an variable gap that utilizes several concepts referred to above is Dr. Pintos optically controlled vacuum energy transducer. By optically pumping the cavity with a microlaser as the gap spacing is varied, the total work done by the Casimir force along a closed path that includes appropriate transformations does not vanishIn the event of no other alternative explanations, one should conclude that major technological advances in the area of endless, by-product free-energy production could be achieved. More analysis on this revolutionary invention will be presented in Chapter 4.
ZPE Patent Review
For any researcher reviewing the
literature for an invention design such as energy transducers, it is well-known
in the art that it is vital to perform a patent search. In 1987, Werner and
Sven from
In 1996, Jarck Uwe from
On Dec. 31, 1996 the conversion
of ZPE was patented for the first time in the Figure 9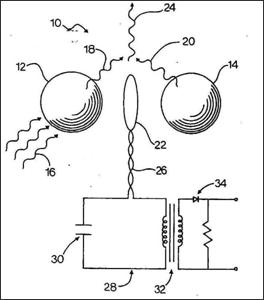 frequency that ZPE offers, which by some
estimates, corresponds to the Planck frequency of 1043 Hz. We do not
have any apparatus to amplify or even oscillate at
frequency that ZPE offers, which by some
estimates, corresponds to the Planck frequency of 1043 Hz. We do not
have any apparatus to amplify or even oscillate at
that frequency currently. For example, gigahertz radar is only
1010 Hz or so. Visible light is about 1014 Hertz and
gamma rays reach into the 20th power, where the wavelength is smaller than the
size of an atom. However, that's still a long way off from the 40th power. The
essential innovation of the Mead patent is the beat frequency generation
circuitry, which creates a lower frequency output signal from the ZPE input.
Another
patent that utilizes a noticeable ZPE effect is the AT&T Negative
Transconductance Device by inventor, Federico Capasso (
Grigg's Hydrosonic Pump is
another patent (
Joseph Yater patented his Reversible Thermoelectric Converter with Power Conversion of Energy Fluctuations (#4,004,210) in 1977 and also spent years defending it in the literature. In 1974, he published Power conversion of energy fluctuations. In 1979, he published an article on the Relation of the second law of thermodynamics to the power conversion of energy fluctuations and also a rebuttal to comments on his first article. It is important that he worked so hard to support such a radical idea, since it appears that energy is being brought from a lower temperature reservoir to a higher one, which normally violates the 2nd law. The basic concept is a simple rectification of thermal noise, which also can be found in the Charles Brown patent (#3,890,161) of 1975, Diode array for rectifying thermal electrical noise.
Many companies are now very interested in such processes for powering nanomachines. While researching this ZPE thesis, I attended the AAAS workshop by IBM on nanotechnology in 2000, where it was learned that R. D. Astumian proposed in 1997 to rectify thermal noise (as if this was a new idea). This apparently has provoked IBM to begin a nanorectifier development program.
Details of some of these and other inventions are analyzed in Chapter 4.
ZPE and Sonoluminescence
Does sonoluminescence (SL) tap ZPE? This question is based upon the experimental results of ultrasound cavitation in various fluids which emit light and extreme heat from bubbles 100 microns in diameter which implode violently creating temperatures of 5,500 degrees Celsius. Scientists at UCLA have recently measured the length of time that sonoluminescence flashes persist. Barber discovered that they only exist for 50 picoseconds (ps) or shorter, which is too brief for the light to be produced by some atomic process. Atomic processes, in comparison, emit light for at least several tenths of a nanosecond (ns). To the best of our resolution, which has only established upper bounds, the light flash is less than 50 ps in duration and it occurs within 0.5 ns of the minimum bubble radius. The SL flashwidth is thus 100 times shorter than the shortest (visible) lifetime of an excited state of a hydrogen atom.
Critical to the understanding of the nature of this light spectrum however, is what other mechanism than atomic transitions can explain SL. Dr. Claudia Eberlein in her pioneering paper 'Sonoluminescence and QED' describes her conclusion that only the ZPE spectrum matches the light emission spectrum of sonoluminescence, and could react as quickly as SL. She thus concludes that SL must therefore be a ZPE phenomena. It is also acknowledged that Schwinger proposed a physical mechanism for sonoluminescence in terms of photon production due to changes in the properties of the quantum-electrodynamic (QED) vacuum arising from a collapsing dielectric bubble.
Gravity and Inertia Related to ZPE
Another dimension of ZPE is found in the work
of Dr. Harold Puthoff, who has found that gravity is a zero-point-fluctuation
force, in a prestigious Physical Review article that has been largely
uncontested.
He points out that the late Russian physicist, Dr. Sakharov regarded
gravitation as not a fundamental interaction at all, but an induced effect
that's brought about by changes in the vacuum when matter is present. The interesting part about this is that the
mass is shown to correspond to the kinetic energy of the zero-point-induced
internal particle jittering, while the force of gravity is comprised of the
long ZPE wavelengths. This is in the
same category as the low frequency, long range forces that are now associated
with Van der
Referring to the inertia
relationship to zero-point energy, Haisch et al. find that first of all, that
inertia is directly related to the Lorentz Force which is used to describe
Faraday's Law.
As a result of their work, the Lorentz Force now has been shown to be directly
responsible for an electromagnetic resistance arising from a distortion of the
zero-point field in an accelerated frame. They also explain how the magnetic
component of the Lorentz force arises in ZPE, its matter interactions, and also
a derivation of
Haisch et al. present an understanding as to why force and acceleration should be related, or even for that matter, what is mass. Previously misunderstood, mass (gravitational or inertial) is apparently more electromagnetic than mechanical in nature. The resistance to acceleration defines the inertia of matter but interacts with the vacuum as an electromagnetic resistance. To summarize the inertia effect, it is connected to a distortion at high frequencies of the zero-point field. Whereas, the gravitational force has been shown to be a low frequency interaction with the zero point field.
Recently, Alexander Feigel has proposed that the momentum of the virtual photons can depend upon the direction in which they are traveling, especially if they are in the presence of electric or magnetic fields. His theory and experiment offers a possible explanation for the accelerated expansion of distant galaxies.
Heat from ZPE
In what may seem to appear as a major contradiction, it has been proposed that, in principle, basic thermodynamics allows for the extraction of heat energy from the zero-point field via the Casimir force. However, the contradiction becomes resolved upon recognizing that two different types of thermodynamic operations are being discussed. Normal thermodynamically reversible heat generation process is classically limited to temperatures above absolute zero (T > 0 K). For heat to be generated at T = 0 K, an irreversible thermodynamic operation needs to occur, such as by taking the systems out of mechanical equilibrium. Examples are given of theoretical systems with two opposite charges or two dipoles in a perfectly reflecting box being forced closer and farther apart. Adiabatic expansion and irreversible adiabatic free contraction curves are identified on a graph of force versus distance with reversible heating and cooling curves connecting both endpoints. Though a practical method of energy or heat extraction is not addressed in the article, the basis for designing one is given a physical foundation.
A summary of all three ZPE effects introduced above (heat, inertia, and gravity) can be found in the most recent Puthoff et al. publication entitled, Engineering the Zero-Point Field and Polarizable Vacuum for Interstellar Flight. In it they state, One version of this concept involves the projected possibility that empty space itself (the quantum vacuum, or space-time metric) might be manipulated so as to provide energy/thrust for future space vehicles. Although far-reaching, such a proposal is solidly grounded in modern theory that describes the vacuum as a polarizable medium that sustains energetic quantum fluctuations. A similar article proposes that monopolar particles could also be accelerated by the ZPF, but in a much more effective manner than polarizable particles. Furthermore, the mechanism should eventually provide a means to transfer energyfrom the vacuum electromagnetic ZPF into a suitable experimental apparatus. With such endorsements for the use of ZPE, the value of this present study seems to be validated and may be projected to be scientifically fruitful.
Summary
To summarize the scientific literature review, the experimental evidence for the existence of ZPE include the following:
Anomalous magnetic moment of the electron
Ground state of the hydrogen atom
Plancks blackbody radiation equation
The apparent discrepancy in the understanding of the concepts behind ZPE comes from the fact that ZPE evolves from classical electrodynamics theory and from quantum mechanics. For example, Dr. Frank Mead (US Patent #5,590,031) calls it 'zero point electromagnetic radiation energy' following the tradition of Timothy Boyer who simply added a randomizing parameter to classical ZPE theory thus inventing stochastic electrodynamics (SED). Lamoreaux, on the other hand, refers to it as 'a flux of virtual particles', because the particles that react and create some of this energy are popping out of the vacuum and going back in. The New York Times simply calls it 'quantum foam.' But the important part about it is from Dr. Robert Forward, 'the quantum mechanical zero point oscillations are real.'
In this chapter, the methods used in this research feasibility study will be reviewed, including the approach, the data gathering method, the database selected for analysis, the analysis of the data, the validity of the data, the uniqueness (originality) and limitations of the method, along with a brief summary.
Approach
The principal argument for the feasibility study of zero-point energy extraction is that it provides a systematic way of evaluating the fundamental properties of this phenomena of nature. Secondly, research into the properties of ZPE offer an opportunity for innovative application of basic principles of energy conversion. These basic transduction methods fall into the disciplines of mechanical, fluidic, thermal, and electrical systems. It is well-known that these engineering systems find application in all areas of energy generation in our society. Therefore, it is reasonable that this study utilize a systems approach to zero-point energy conversion while taking into consideration the latest quantum electrodynamic findings regarding ZPE.
There are several important lessons that can be conveyed by a feasibility study of ZPE extraction.
It permits a grounding of observations and concepts about ZPE in a scientific setting with an emphasis toward engineering practicability.
It furnishes information from a number of sources and over a wide range of disciplines, which is important for a maximum potential of success.
It can provide the dimension of history to the study of ZPE thereby enabling the investigator to examine continuity and any change in patterns over time.
It encourages and facilitates, in practice, experimental assessment, theoretical innovation and even fruitful generalizations.
It can offer the best possible avenues, which are available for further research and development, for the highest probability of success.
A feasibility study enables an investigation to take place into every detail of the phenomena being researched. The feasibility study is an effective vehicle for providing an overview of the breadth and depth of the subject at hand, while providing the reader an opportunity to probe for internal consistency.
What is a Feasibility Study?
A feasibility study is a complete examination of the practicability of a specific invention, project, phenomena, or process. It strives to provide the requisite details necessary to support its conclusion concerning the possibility or impossibility of accomplishing the goal of the research study. As such, it takes an unbiased viewpoint toward the subject matter and reflects a balanced presentation of the facts that are currently available in the scientific literature.
Feasibility studies are the hallmark of engineering progress, often saving investors millions of dollars, while providing a superior substitute for risk assessment. Therefore, such studies are required before any consideration is made of the investment potential of an invention, project, process, or phenomena by venture capitalists. Feasibility studies thus provide all of the possible engineering details that can be presented beforehand so that the construction stage can proceed smoothly and with a prerequisite degree of certitude as to the outcome.
Feasibility studies can also provide a wealth of information just with the literature survey that is an integral part of the research. Along with the survey, an expert engineering and physics assessment is usually provided regarding the findings reported in the literature and how they directly relate to the capability of the process, phenomena, project, or invention to be put into effect.
As such, a feasibility study offers the best possible original research of the potential for successful utilization, with a thick descriptive style so necessary for an accurate and honest judgment.
A good feasibility study will contain clear supporting evidence for its recommendations. Its best to supply a mix of numerical data with qualitative, experience-based documentation (where appropriate). The report should also indicate a broad outline of how to undertake any recommended development work. This will usually involve preparing an initial, high-level project plan that estimates the required project scope and resources and identifies major milestones. An outline plan makes everyone focus more clearly on the important implementation issues and generate some momentum for any subsequent work. This is especially true if feasibility teams suspect that the development itself will become their baby. A sound, thorough feasibility study will also ease any subsequent development tasks that gain approval. The feasibility study will have identified major areas of risk and outlined approaches to dealing with these risks. Recognising the nature of feasibility projects encourages the successful implementation of the best ideas in an organisation and provides project managers with some novel challenges.
Data Gathering Method
The method used in this feasibility study is the same that is used in pure as well as applied research. Through a review of the scientific literature, certain approaches to the conversion of zero-point energy into useful work demonstrate more promise and engineering feasibility than others. Combining the evaluation with the known theories and experimental discoveries of zero-point energy and the authors professional engineering knowledge of electromechanical fabrication, a detailed recommendation and assessment for the most promising and suitable development is then made. This procedure follows the standard method used in most feasibility studies. , ,
Database Selected for Analysis
The database for this study consists of mostly peer-reviewed physics journals, engineering journals, science magazines, patent literature, textbooks, which are authored by physicists and engineers.
Analysis of Data
The analysis of the data is found in Chapter 4, where the findings are explored. The most promising possibilities, from an engineering standpoint, are the zero-point energy conversion concepts that are past the research stage or the proof-of-principle stage and into the developmental arena. Using the scientific method, a thorough examination of the data is presented, with physics and engineering criteria, to determine the feasibility of zero-point energy extraction.
Validity of Data
The data used in this study can be presumed to be valid beyond a reasonable doubt. Ninety years ago, when zero-point energy was first discovered, the validity of the data may have been questioned. However, after so much experimental agreement with theory has followed in the physics literature, it can be said that the data has stood the test of time. Furthermore, in the past decade, there has been a dramatic increase in the number of journal publications on the subject of zero-point energy, demonstrating the timeliness and essential value of this study. Excluding any anomalous findings that have not been replicated or verified by other scientists, it can be presumed that the data presented in this feasibility study represents the highest quality that the scientific community can offer.
Uniqueness and Limitations of the Method
The method applied in this study, though it appears to be universal in its approach, is being applied for the first time to determine the utility of zero-point energy extraction. Only through experimental verification can the method be validated. However, many intermediate steps required for utilization have already been validated by experiment, as mentioned in the above sections.
As with any study of this nature, certain limitations are inherent in the method. The feasibility study draws from a large database and involves a great number of variables, which is, in itself, a limitation. The nature of ZPE is also a limitation because it is so unusual and foreign to most scientists, while many standard testing methods used for other fields and forces fail to reveal its presence.
These variables and limitations have been minimized to every extent possible.
Summary
The method used in this feasibility study is the application of the basic principles of energy conversion in the mechanical, fluidic, thermal, and electromagnetic systems to zero-point energy research. It is a systems approach that has a fundamental basis in the scientific method. By reviewing journal articles and textbooks in the physics and engineering field of zero-point energy, certain data has been accumulated. The analysis of the data is conducted in a critical manner with an approximate rating system in order to evaluate the practical applications of both theory and experiment, and the likelihood of success for energy conversion. It is believed that this is the first time such an approach has been used and applied to the field of zero-point energy conversion. As such, new and exciting conclusions are bound to emerge.
Introduction to Vacuum Engineering
The emerging discipline of vacuum engineering encompasses the present investigation into energy conversion modalities that offer optimum feasibility. It is believed by only a minority of physicists that the vacuum can be engineered to properly facilitate the transduction of energy to useful work. In this chapter, the most promising inventions and processes are examined and analyzed according to the methodology outlined in Chapter 3.
The scope of this feasibility study is detailed in Chapter 1 and will include zero-point energy conversion methodologies in the areas of electromagnetism, fluid mechanics, thermodynamics, mechanical physics, and some quantum theories.
Vacuum engineering considerations often exhibit a particular bias toward wave or particle. It is difficult or perhaps impossible to design a zero-point energy converter that will utilize both wave and particle aspects of the quantum vacuum. Therefore, experimental ZPE conversions will center upon one or the other approach, except where the size of the transducer varies.
Electromagnetic Energy Conversion
Treating
the quantum vacuum initially as an all-pervading electromagnetic wave with a
high bandwidth is a classical physics approach. Among various examples, the
most intriguing is a
the energy density increases with frequency (col. 7, line 63),
the spheres are preferably microscopic in size (col. 8, line 3),
a volume of close proximity spheres enhances output (col. 8, line 20),
resonant
spherical structures are of different size so that the secondary fields will be a lower frequency than the incident radiation (col. 3, line 7),
the converter circuitry may also include a transformer for voltage optimization and possibly a rectifier to convert the energy into a direct current (col. 3, line 30),
the system also includes an antenna which receives the beat frequency (col. 7, line 35).
It is noted in the patent that zero point radiation is homogeneous and isotropic as well as ubiquitous. In addition, since zero point radiation is also invariant with respect to Lorentz transformation, the zero point radiation spectrum has the characteristic that the intensity of the radiation at any frequency is proportional to the cube of that frequency (col. 1, line 30). This sets the stage for an optimum design of the highest frequency collector possible that the inventors believe will work anywhere in the universe.
Another area of interest upon review is the opinion of the inventors that, At resonance, electromagnetically induced material deformations of the receiving structures produce secondary fields of electromagnetic energy therefrom which may have evanescent energy densities several times that of the incident radiation (col. 2, line 65). However, this does not seem to be a physically justifiable statement, nor is it defended anywhere else in the patent. Furthermore, the discussion diverges and instead proceeds toward the formation of beat frequencies which are produced through interference resulting in the sum and difference of two similar frequencies. It is noted that the subtraction of the frequencies from two receivers of slightly different size is of primary importance to the invention claimed (col. 3, line 7).
The engineering considerations in the patent include the statement that packing a volume with such spheres in close proximity could enhance the output of energy (col. 8, line 20). The enhancement referred to here is understood to mean the multiplied effect from having several interference sources for the beat frequency production and amplification. Upon researching this aspect of the invention, it is found however, that scattering by a collection of scatterers can actually reduce the output of energy, especially if the spheres are randomly distributed. In that case, an incoherent superposition of individual contributions will have destructive instead of constructive interference. A large regular array of scatterers, even if transparent, tends to absorb rather than scatter, such as a simple cubic array of scattering centers in a rock salt or quartz crystal.
 This crucial feature of the patent involving
the receivers output involves a method for analyzing electromagnetic or Mie
scattering from dielectric spheres
(col. 4, line 60). The patent relies upon a report detailing the calculations
by Cox (which has been obtained from the inventor) of two infinite series
equations for the electric and magnetic components of the spherical reflection
of incident electromagnetic waves.
The report, summarized in the patent, utilizes spherical Bessel functions to
solve two pairs of inhomogeneous equations for the components of radiation
scattering from a dielectric sphere.
This crucial feature of the patent involving
the receivers output involves a method for analyzing electromagnetic or Mie
scattering from dielectric spheres
(col. 4, line 60). The patent relies upon a report detailing the calculations
by Cox (which has been obtained from the inventor) of two infinite series
equations for the electric and magnetic components of the spherical reflection
of incident electromagnetic waves.
The report, summarized in the patent, utilizes spherical Bessel functions to
solve two pairs of inhomogeneous equations for the components of radiation
scattering from a dielectric sphere.
![]() For
a particular radius of the spheres, resonance will occur at a corresponding
frequency. In the patent, with the sphere diameter set equal to 2 microns (2 x 10-6 m) one solution is
found as an example (col. 7, line 10). The resonant frequency is calculated to
be about 9 x 1015 radians per second (1.5 x 1014 Hz),
which is the corresponding frequency calculated from the wavelength ( c = f
λ ) that can be assumed to classically resonate with a sphere of that
size, as also found in the light spectrum chart (Figure 10). This serves as one
check for the feasibility of the patents prediction, since it is within a
power of ten of this answer for a microsphere. The spacing between spheres,
seen in Figure 14, may resonate at a higher harmonic.
For
a particular radius of the spheres, resonance will occur at a corresponding
frequency. In the patent, with the sphere diameter set equal to 2 microns (2 x 10-6 m) one solution is
found as an example (col. 7, line 10). The resonant frequency is calculated to
be about 9 x 1015 radians per second (1.5 x 1014 Hz),
which is the corresponding frequency calculated from the wavelength ( c = f
λ ) that can be assumed to classically resonate with a sphere of that
size, as also found in the light spectrum chart (Figure 10). This serves as one
check for the feasibility of the patents prediction, since it is within a
power of ten of this answer for a microsphere. The spacing between spheres,
seen in Figure 14, may resonate at a higher harmonic.
The Cox report, supplied to this author by Dr. Mead, ends with an offer of general guidance, which is not found in the patent, regarding research in this area: Much work still remains in finding more resonances and in studying other areas of the theory. A source of EM radiation having a broad enough range of frequencies to achieve resonances between two chosen spheres needs to be selected. Then, one should analyze the beat frequency produced by the interaction of the two resonant waves, as well as the effect of separation distance of the two spheres on the beat frequency. Finally, a method of rectifying this beat frequency should be established using currently available equipment, if possible. It is also important to know how much energy is available at the resonant points. As a practical matter, manufacturing processes must be investigated that would allow structures to be fabricated with close enough tolerances to be of use.
It is not
difficult to examine each of the above-mentioned recommendations offered by the
report, in order to assess the feasibility of this ZPE invention. First of all,
the analysis used by the inventors in the patent and the report depends upon
one rather involved and somewhat obscure approach to
Figure 11 Incident Wave and Sphere Figure
12
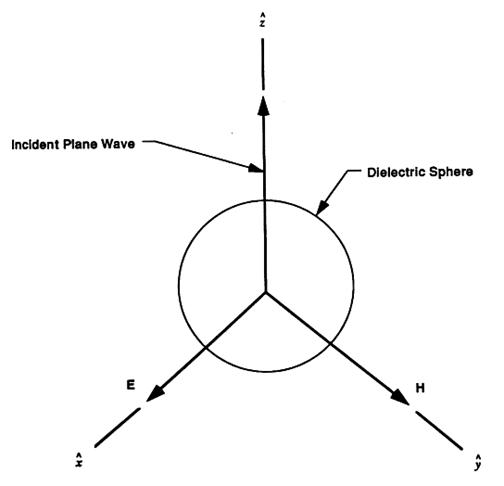
scattering from an older textbook. The main area of concern addressed in this
report is the interaction of electromagnetic radiation with a
dielectric sphere; i.e., the diffracting of a plane wave by a sphere, more
commonly known as Mie scattering.
It is assumed that the sphere is made of a homogeneous material and that the
medium surrounding the sphere is a vacuum. The incident radiation is assumed to
be a plane wave propagating in the z-direction. Electrical vibrations of the
incident wave are assumed to occur in the x-direction, with magnetic vibrations
in the y-direction (see Figure 11). As explained in Stratton,
a forced oscillation of free and bound charges, synchronous with the applied
field, arises when a periodic wave falls incident upon a body, regardless of
the spheres
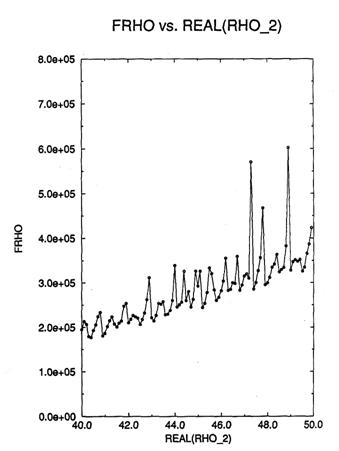 material. This creates a secondary field in
and around
material. This creates a secondary field in
and around
the body. The vector sum of these primary and secondary fields
gives the value of the overall field. In theory, a transient term must be added
to account for the failure of the boundary conditions to hold during the onset
of forced oscillations. However, in practice it is acceptable to consider only
the steady-state, synchronous term because the transient oscillations are
quickly damped by absorption and radiation losses.
While this introductory viewpoint is sophisticated, it is also rudimentary, classical physics. The calculations used by Stratton and Cox become cumbersome however, aimed toward the supposedly obscure resonance between two spheres, though only one sphere is analyzed. The culmination of the work solves for RHO (ρ) which is defined as the propagation constant multiplied by the radius of the dielectric sphere and alternately defined as the radius times the frequency of interest divided by the speed of light c. The report and patent furthermore emphasize resonant peaks, seen in Figure 12, which are claimed to be worthy of special design considerations. However, it is noted that these peaks of FRHO are less than a power of ten from baseline, which, considering standard engineering practice, will not warrant special design attention. Considering feasibility analysis, if each sphere successfully amplified free energy from the vacuum, the improvement in output from resonance beat frequency design can only be a secondary consideration for quality management to reduce waste and improve efficiency after prototype manufacture, not a primary focus patent and laboratory reports.
Secondly, neither the patent nor the report
mentions the power density of the scattered energy even once. It is
assumed that
These two issues create the distinct impression that this invention is presented in such a way that distracts attention from the essential issue of quantitative energy extraction.
With that preliminary assessment, the following physics analysis separates this theoretical ZPE invention into four spheres of interest:
microsphere: micron-sized (10-6 m) electrolithography,
nanosphere: nanometer-sized (10-9 m) molecular nanotechnology,
picosphere: picometer-sized (10-12 m) atomic technology,
femtosphere: femtometer-sized (10-15 m) nuclear technology.
However, only the first two or three are amenable to electromagnetic analysis, with corresponding wavelengths of interest. The fourth category requires quantum analysis. The relative comparison of λ > R, λ = R, or λ < R may only differ if a resonance occurs near R = λ. The diameter (= 2R) of the sphere is most often considered to resonate with the fundamental wavelength of interest but a factor of two may not be significant in every case. In quantum mechanics however, de Broglies standing matter waves correspond to the Bohr quantization condition for angular momentum, and are equal to an integral multiple of the circumference (= 2pR) of an electron orbit of an atom.
Scattering and absorption of electromagnetic radiation by a conducting or dielectric sphere varies considerably in classical physics. Therefore, two additional distinctions, dielectric or conductor, should also be considered for microspheres and nanospheres. A general benefit of the ubiquitous zero-point electromagnetic radiation in regards to scattering is that with all of the spheres, no shadow or transition regions need to be considered. Based on this nature of the ZPF, all parts of the surface of the sphere considered are in the illumined region, which simplifies the analysis.
![]()
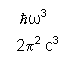 Regarding
the patents reference to an increase of energy with frequency (col. 7, line
62), in reality, the spectral energy density of the ZPF depends on the third
power of frequency:
Regarding
the patents reference to an increase of energy with frequency (col. 7, line
62), in reality, the spectral energy density of the ZPF depends on the third
power of frequency:
![]()
ρo(ω ) =
which is integrated further on to yield Equation (21) for a band of frequencies. It is noted that Equation (16) is directly related to the third order dependence of radiation reaction, according to the fluctuation-dissipation theorem.
It is agreed that the general design criteria of the patent is feasible: the spheres must be small in direct proportion to the wavelength of the high frequencies of the incident electromagnetic radiation at which resonance is desirably obtained (col. 7, line 66).
Figure 13 beating phenomena
Before proceeding with
individual categories of spherical sizes and wavelengths, it is useful to
briefly review the beating phenomena as it is known in vibrational physics,
whether in mechanical or electromagnetic systems. Starting with two harmonic
motions of the same amplitude but of slightly different frequencies imposed
upon a vibrating body, the amplitudes of the two vibrations can be expressed as
x1 = A cos ωt and x2
= A cos (ω + Δω)t . Adding these together and using a
trigonometry identity, it is found that the composite amplitude x = x1
+ x2 is mathematically expressed as:
x = cos (ω + Δω/2)t . (17)
It is noted that Δω is normally a constant in most systems while ω may vary. Two observations for application to the ZPE patent being examined are the following:
the amplitude of the composite vibration is doubled (2A)
the beat frequency of the vibration is fb = Δω/2p Hz .
The period (wavelength) of the beating phenomena is T = 1/ fb (see Figure 13).
Also common in electronic and optical systems, where it is called heterodyning, the beating phenomena permits reception at lower frequencies where a local oscillator is used to interfere with the signal.
Microsphere Energy Collectors
Figure 14 semiconductor spheres
The micron-sized sphere (microsphere) is already mentioned in
the patent and in the Cox report. Looking at some of the risks involved, it is
assumed to have a radius R = 10-6 m but the second adjacent sphere
will unpredictably vary by at least 5%, due to manufacturing tolerances. A
primary example in the patent, general engineering considerations would
question the advantage of designing for a single beat frequency in this case,
which tends to limit the bandwidth and energy output. Using Figure 10 as
mentioned previously, we find
 that a wavelength of a micrometer (micron)
resonates with a frequency of 1014 Hz, which is in the optical
region. In this region, it would be prudent to utilize photovoltaic (PV)
technology for the converter 222 in Figure 14, which is already developed for
the conversion of optical radiation to electrical energy, which for silicon
photovoltaic cells, peaks around 0.8 micron in optical wavelength.
With that in mind, Figure 10 implies that the sphere might be a tenth of a
micron in size instead, with a wavelength in the UV region. Then, at the
most, a 10% variation in size will create a maximum beat frequency of about 1 x
1014 Hz. However, the feasibility of inducing a prominent beat
frequency with broadband ZPE electromagnetic wave scattering by uncoupled
dielectric spheres has to be questioned in this case. Because the beating
phenomena, which only doubles the amplitude, will not be significant in
this regime, individual spheres constructed adjacent to a micron-sized PV
converter, may be preferable, as seen in Figure 14 from the patent.
that a wavelength of a micrometer (micron)
resonates with a frequency of 1014 Hz, which is in the optical
region. In this region, it would be prudent to utilize photovoltaic (PV)
technology for the converter 222 in Figure 14, which is already developed for
the conversion of optical radiation to electrical energy, which for silicon
photovoltaic cells, peaks around 0.8 micron in optical wavelength.
With that in mind, Figure 10 implies that the sphere might be a tenth of a
micron in size instead, with a wavelength in the UV region. Then, at the
most, a 10% variation in size will create a maximum beat frequency of about 1 x
1014 Hz. However, the feasibility of inducing a prominent beat
frequency with broadband ZPE electromagnetic wave scattering by uncoupled
dielectric spheres has to be questioned in this case. Because the beating
phenomena, which only doubles the amplitude, will not be significant in
this regime, individual spheres constructed adjacent to a micron-sized PV
converter, may be preferable, as seen in Figure 14 from the patent.
Scattering contributions by these microspheres can be analyzed from classical electrodynamic equations that apply. The range λ > R is scattering of electromagnetic waves by systems whose individual dimensions are small compared with a wavelength, which is a common and important occurrence. Without polarization of the incident wave, since ZPE radiation is ubiquitous, it will not contribute to dipole or multipole formation on the sphere. Assumptions include a permeability μ = 1 and a uniform dielectric constant Є which varies with frequency. Energy output is calculated by the total scattering cross section σ. With units of area, σ is an area normal to the incident beam which intercepts an amount of incident power equal to the scattered power.
The total scattering cross section of a dielectric sphere for λ > R is,
![]() │Є 1│2
│Є 1│2
│Є + 2│2

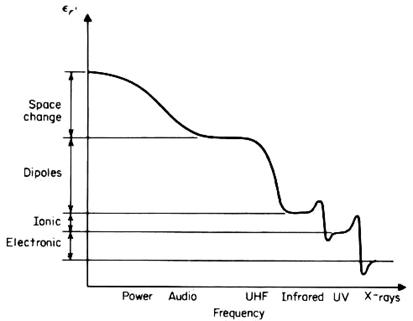 visible range, essentially independent of
temperature from 0 to 100C.
With this information in mind, a graph of the behavior with frequency is also
shown in Figure 15. A declining Є with frequency can only make Equation
(18) even smaller as Є tends toward the limit of 1 (where the permittivity
equals Єo ).
visible range, essentially independent of
temperature from 0 to 100C.
With this information in mind, a graph of the behavior with frequency is also
shown in Figure 15. A declining Є with frequency can only make Equation
(18) even smaller as Є tends toward the limit of 1 (where the permittivity
equals Єo ).
As an example of the total cross section for scattering by a relatively good dielectric, Є = 3 can be chosen. Then, with f = 1014 Hz and R = 0.1 x 10-6 m (thus keeping λ > R), Equation (18) is found to yield σ = 2.6 x 10-17 m2. Dividing σ by the actual cross sectional area of a microsphere ( pR2 ) for comparison, scattering by a dielectric sphere of optical frequency electromagnetic radiation yields a loss of about 8 x 10-6 in power.
In comparison, for λ > R, small conducting spheres have a total scattering cross section that is significantly larger, where
σ = ⅓ 10p b4 R6 . (19)
There is an advantage of using conducting spheres in place of the dielectric spheres which is more significant than designing for the doubling effect from possible beat frequencies. The cross section σ for a one-tenth micron-sized conducting sphere (R = 0.1 x 10-6 m) with visible light incident (f = 1014 Hz) yields about 2 x 10-16 m2 for λ > R. Dividing this as before by the actual cross sectional area yields only 6 x 10-5 loss of power or ten times better than the dielectric scattering cross section.

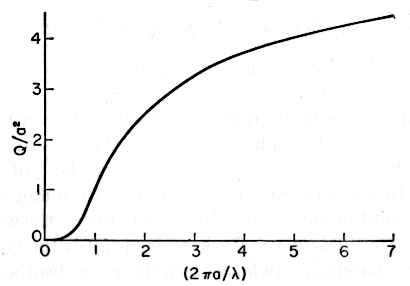 While both of these total cross section
calculations still may seem very low, there seems to be an explanation for it.
Since they were still within a power of ten from λ = R, Figure 16 shows
there is an interference scattering effect for plane waves, within a few
wavelengths of this region. Utilizing the spherical Bessel function expansion
for a plane wave, similar to the inventor Mead, the solution with amplitudes
and phases is found for the boundary condition that the wave function is zero
at R = a but the radial velocity of the wave is zero at R = 0. As seen in
Figure 16 (the textbook uses Q for total cross section), the surprise is that
in the region of λ = 2pR
and smaller (<1 on the abscissa), the total cross section becomes very
small, tending to zero. The graph, however, reflects the boundary conditions
used, such as the radial velocity vr of the ratio S (of scattered
intensity to incident intensity) = 0, the total cross section calculation with
the proper Bessel function tends toward the limit of 2pR2
for λ <<R, which is twice the actual cross sectional area. However,
for very long wavelengths
While both of these total cross section
calculations still may seem very low, there seems to be an explanation for it.
Since they were still within a power of ten from λ = R, Figure 16 shows
there is an interference scattering effect for plane waves, within a few
wavelengths of this region. Utilizing the spherical Bessel function expansion
for a plane wave, similar to the inventor Mead, the solution with amplitudes
and phases is found for the boundary condition that the wave function is zero
at R = a but the radial velocity of the wave is zero at R = 0. As seen in
Figure 16 (the textbook uses Q for total cross section), the surprise is that
in the region of λ = 2pR
and smaller (<1 on the abscissa), the total cross section becomes very
small, tending to zero. The graph, however, reflects the boundary conditions
used, such as the radial velocity vr of the ratio S (of scattered
intensity to incident intensity) = 0, the total cross section calculation with
the proper Bessel function tends toward the limit of 2pR2
for λ <<R, which is twice the actual cross sectional area. However,
for very long wavelengths ![]() compared to the radius (λ >>R) the
total cross section for plane
compared to the radius (λ >>R) the
total cross section for plane
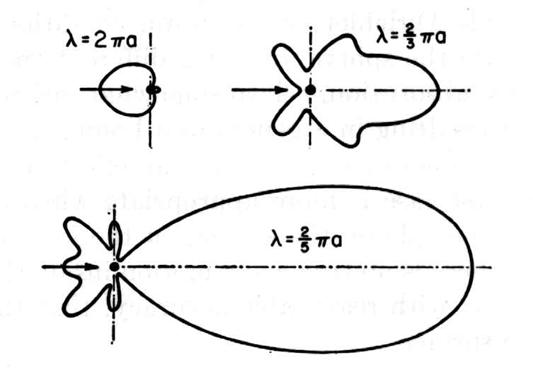
wave scattering by a sphere tends toward 4pR2 which is four
times the actual cross sectional area.
Also confirmed from Figure 17, based on the same text with a Bessel function treatment of a plane wave incident (from the left) on a rigid sphere, the scattered intensity grows larger with smaller wavelength, instead of exhibiting a trend toward resonance when λ ≈ R, tending to be spherically symmetrical in the limit where bR à 0, S à 1, and σ à 4pR2. These figures seem to contradict the inventors assertion of a ZPE electromagnetic resonance with a microsphere and any number of microspheres in close proximity. Furthermore, the penetration of electromagnetic waves throughout dielectric spheres is another complication which is treated in detail in the above-mentioned theoretical physics text, including a complex index of refraction when required, to account for transmission, reflection, and absorption. These two issues diminish the feasibility of the inventors microsphere design significantly.
In the region of λ <R, classical ray theory applies since the wavelength is short compared to the radius of curvature. Fresnel equations can also be utilized, treating the surface as locally flat. This argument also leads to the standard description in physics of specular reflection.
![]()
![]()
To show the value of Bessel function analysis of plane wave scattering and the
strong directional dependence, a graph of the differential cross section is
plotted in Figure 18. Considering the previously mentioned advantage of using conducting
spheres of the micron size, the analysis is also more straightforward.
Under these circumstances, the tangential magnetic fields and normal electric
fields of the electromagnetic wave will be approximately equal to the incident
wave.
The differential backward scattering of the incident radiation, for λ <
R 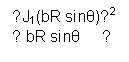
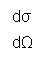 and
θ < 10/bR is found to be,
and
θ < 10/bR is found to be,
![]()
![]()
= R2(bR)2 (20)
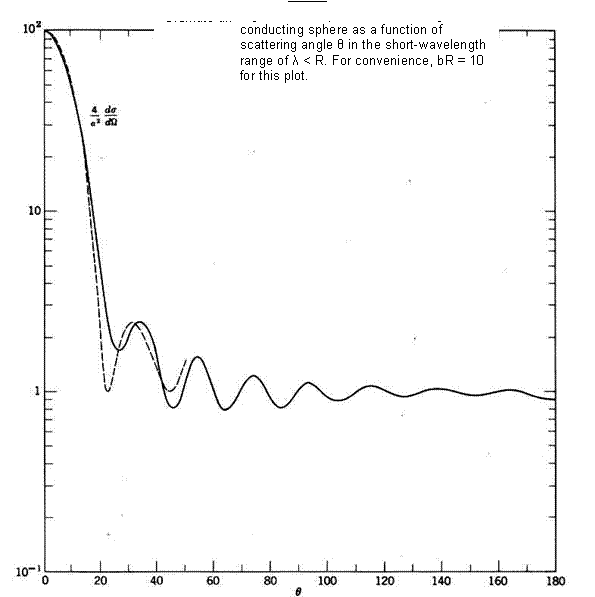
where J1 is a Bessel function of the first kind of order one. The
forward differential scattering for θ >> 1/bR (higher θ angles) is simply R2/4.
A plot of Equation (20), for the smaller angles, is the dashed line in Figure
18, with the exact solution as the solid line. Destructive interference is
noted where it dips below unity.
The peak in the graph of Figure 18 indicates a strong reflection
back-scattering for a conductive sphere. This is a common phenomenon since
silver, a very good conductor, is used often for coating glass to create
mirrors. The conductive surface allows the electric field vector of the
electromagnetic wave to oscillate freely upon contact, with very little
resistance, thus creating the reflective wave.
Such electromagnetic radiation scattering is distinguished from Thomson scattering, Rayleigh scattering, Coulomb scattering, Compton and Rutherford scattering, which also use cross section formulae as well. Each of these, more common with particle scattering, will be discussed in the following sections.
It should be emphasized that the same two σ limits discussed above, 2pR2 and 4pR2, for small wavelengths (λ <<R) and large wavelengths (λ >>R) respectively, are also derived in quantum mechanics using the method of partial waves for scattering of wave packets by a perfectly rigid sphere and thus will also be applied in the further sections to follow.
For feasibility consideration of energy extraction, to collect and transduce the total scattered ZPE radiation from the vacuum flux, it would be necessary to place one sphere at the focus of an evacuated, reflecting 3-D ellipsoid cavity with the PV converter at the other, for example, instead of the spherical cavity the inventors refer to. However, in the interest of maximizing energy output per volume, it may be more convenient to engineer sheets of single spheres placed in alternate planes between planar PV converters, which may unfortunately limit the available ZPF frequencies.
An important calculation for each sphere of interest is to find whether significant scattered zero-point energy is available at these wavelengths. Therefore, the spectral density Equation (16) is integrated as,
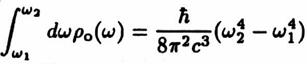
. (21)
For the wavelength range of 0.4 to 0.7 microns (micrometers) in the visible light band, using Equation (8), the radial frequencies can be generated for the integrated energy density equation. Substituting these for ω2 and ω1 we find an energy density of only 22 J/m3 or 22 microjoules/cc which equals approximately 0.24 eV/μm3 (electron volts per cubic micron).
To create a simple standard calculation for the frequency band of each sphere of interest, ω2 is chosen to correspond to the radius R and ω1 is chosen to be 1/10 of that frequency. For a microsphere, with λ = R = 10-6 m, the spectral energy density from Equation (21) is ρ(ω) = 0.62 J/m3 or 3.9 eV/μm3 for the decade range: Δf = 3 x 1013 to 3 x 1014 Hz. From Figure 10, this energy density is also comparable to the photon energy (2 eV) in the visible band.
Nanosphere Energy Scatterers
In the region of λ > R for the scattering by these nano-sized spheres (nanosphere) the classical electrodynamic equations still apply. However, with a radius R of the sphere considered to be 10-9 m, the effect on the ZPF spectral energy density is quite dramatic. In Figure 22, it is noted that 1 nm is in the keV region. A resonant correspondence with the sphere diameter of 2 x 10-9 m equals a full wavelength antenna, the resonant frequency will be in the range of 1 x 1017 Hz. The spectral energy density of ZPE at this frequency is substantially more promising. Using Equation (21), we find that the ZPE spectral energy density is 6.2 x 1011 J/m3, which is a billion times more energy per cubic meter than was available from the ZPF for the micro-sized spheres. Converting to electronvolts per cubic nanometer, it is interesting that the ZPF offers about 390 eV/nm3 which is three orders of magnitude more energy than available to the micron-sized sphere. The advantage as well is that a billion of these spheres will fit into a cubic micrometer, if a collection was found to be coherently constructive with regards to scattering. Vacuum polarization is probably more pronounced at the nanometer dimensions, yielding more ZPE virtual particles which would be expected contribute more significantly to scattering off of nanospheres.
Evaluating Equation (19) at this resonant frequency and radius, it is found that for a conducting nanosphere, the scattering cross section σ = 1 x 1015 m2 for the region λ > R. Comparing with cross-sectional area pR2 for the nanospheres, it is found to be 318 times its cross-sectional area pR2. (The ratio of σ to spherical surface area is also constant σ /4p R2 = 83). This demonstrates that the scattering cross section σ is geometrically correlated to the objects actual cross-sectional area.
For the consideration of λ ≈ 2R, resonance is still not expected to affect the amplitude of scattered radiation appreciably.
For the consideration of λ < R the scattering profile seen in Figure 18 would still apply because quantum mechanical effects become important only when hf ≈ mc2. This may be anticipated for the femtosphere.
![]()
 The
present state of the art for engineering capabilities in the microsphere and
nanosphere regions is illustrated in Figure 19. Called nanoboxes, they are
electrically conductive single crystals of silver, produced at the
The
present state of the art for engineering capabilities in the microsphere and
nanosphere regions is illustrated in Figure 19. Called nanoboxes, they are
electrically conductive single crystals of silver, produced at the
![]()
 Regarding
the scale of 1 nanometer in diameter, such as the nanosphere that is proposed,
the error control may not require a higher tolerance range than quoted above.
As seen in Figure 20, if individual molecular crystals were used for 1 nm
range, they do not vary widely in size.
A sphere of carbon-60, for example, would be a real possibility, though it is
not highly conductive. If metal nanopolygons are used, it is noted that
nonspherical gold and silver nanoparticles absorb and scatter light of
different wavelengths, depending on nanoparticle size and shape.
Regarding
the scale of 1 nanometer in diameter, such as the nanosphere that is proposed,
the error control may not require a higher tolerance range than quoted above.
As seen in Figure 20, if individual molecular crystals were used for 1 nm
range, they do not vary widely in size.
A sphere of carbon-60, for example, would be a real possibility, though it is
not highly conductive. If metal nanopolygons are used, it is noted that
nonspherical gold and silver nanoparticles absorb and scatter light of
different wavelengths, depending on nanoparticle size and shape.
Interestingly, gold and silver nanoparticles have been used as sensors, since they have surface-enhanced Raman scattering and other optical effects peculiar to the ~10- to 100-nm range. Instead, using heavy metal atoms, such as Polonium with a diameter of 0.336 nm should be considered in this section because of superior spherical shape and reproducibility. Polonium may also be an interesting candidate because it is the only element known to crystallize in a primitive cubic unit cell under room temperature conditions. Therefore, the interatomic spacing is also very well known. ZPE virtual particles, or equivalent ZPE electromagnetic radiation, would not be expected to play a large part in scattering off polonium atoms however. Instead, they already are known to contribute to the Lamb shift of the 2p electron levels, with about 1.06 GHz worth of energy. Furthermore, virtual particle scattering contributes the same energy to every state, consisting of e2A2/2mc2 in the nonrelativistic theory with the Hamiltonian, where A is the vector potential. Beat frequencies would be unlikely and very difficult to engineer with polonium atoms since the atoms would normally share the same energy, being at the same temperature, etc.
Picosphere Energy Resonators
In
the picosphere range, it is more likely that some of the key elements of this
patent may be more effectively applied. One of the reasons for this is that up
until this point, there has not been a necessity for lower frequency
scattering. To review some of the transduction methods available, Figure 21
shows some of the standard devices for transducing ionization into electricity.
Note that ionizing 
![]() radiation
can also consist of electromagnetic X-rays or gamma rays since there is
sufficient energy at these frequencies to cause ionization. The method of
ionizing transduction relies upon the production of ion pairs in a gas or solid
by the incidence of radiation. The applied electric field in Figure 21 is an
excitation voltage (Exc.) used to separate the ionized positive and negative
charges to produce an electromotive force.
For the picosphere range, it is also expected that small individual atoms
can be arranged to meet the specifications for the patent more effectively
since nature has much better error tolerances than engineers can manufacture
artificially.
radiation
can also consist of electromagnetic X-rays or gamma rays since there is
sufficient energy at these frequencies to cause ionization. The method of
ionizing transduction relies upon the production of ion pairs in a gas or solid
by the incidence of radiation. The applied electric field in Figure 21 is an
excitation voltage (Exc.) used to separate the ionized positive and negative
charges to produce an electromotive force.
For the picosphere range, it is also expected that small individual atoms
can be arranged to meet the specifications for the patent more effectively
since nature has much better error tolerances than engineers can manufacture
artificially.

![]() The
high frequency electromagnetic spectrum is reproduced in Figure 22, which picks
up where Figure 10 left off, with wavelength decreasing from left to right.
The picosphere with a radius of 10-12 m (1 pm) and a wavelength
equal to its diameter, corresponds to a frequency of 1.5 x 1020 Hz
using Equation (8). Using Einsteins equation E = hf, the photon energy at that
frequency can be found to be about 650 keV which is useful to compare with the
spectral energy density. Using Equation (21), we calculate a spectral energy
density of 6.2 x 1023 J/m3 or 390 keV/pm3.
The
high frequency electromagnetic spectrum is reproduced in Figure 22, which picks
up where Figure 10 left off, with wavelength decreasing from left to right.
The picosphere with a radius of 10-12 m (1 pm) and a wavelength
equal to its diameter, corresponds to a frequency of 1.5 x 1020 Hz
using Equation (8). Using Einsteins equation E = hf, the photon energy at that
frequency can be found to be about 650 keV which is useful to compare with the
spectral energy density. Using Equation (21), we calculate a spectral energy
density of 6.2 x 1023 J/m3 or 390 keV/pm3.
In the range of λ > R the scattering cross section σ = 1 x 1021 m2 is in the same proportion of 318 times sphere cross sectional area.
At the resonant wavelength of λ ≈ 2R, the amplitude of scattering can be expected to be higher. It is also anticipated that here is where the concept of beat frequency may be applied more conveniently, with greater precision than in either larger category. However, since all atomic radii vary between 50 pm (e.g., Helium) and 660 pm (e.g., Cesium), the picosphere with a proposed radius of 1 pm has to be declared to be impractical and therefore, not feasible.
![]()
 In
the range of λ < R the scattering seen in Figures 16 and 17 would still
apply. The diffraction pattern is also very predictable. The intensity
distribution of X-ray diffraction could be correlated to the theoretical
scattering off a sphere from Equation (21). An example is seen in Figure 23
where the wavelength of the X-rays is 71 pm and the target is an aluminum atom,
which has an atomic radius of 182 pm.
In
the range of λ < R the scattering seen in Figures 16 and 17 would still
apply. The diffraction pattern is also very predictable. The intensity
distribution of X-ray diffraction could be correlated to the theoretical
scattering off a sphere from Equation (21). An example is seen in Figure 23
where the wavelength of the X-rays is 71 pm and the target is an aluminum atom,
which has an atomic radius of 182 pm.
If a smaller target on the order of a picosphere were used, it is expected that the scattering pattern would be the same for λ < R.
In this region, the need for a heterodyned frequency might emerge if, for example, the ionization transducers of Figure 21 were not configured for high efficiency capturing of the ZPE scattered radiation. However, the production of a beat frequency that also resonates with the geometry of an array of atoms may be problematic, for two reasons. The array would preferably need to be a 2-D sheet only one atom thick, such as thin metal foil used for diffraction studies, to prevent destructive interference of the ZPF scattering. Secondly, the real barrier to creating a useful ZPE beat frequency atomic array is producing picospheres that vary reliably in one part in one thousand with a maximum error tolerance of one part in ten thousand. An avenue of speculative physics would require the engineer to estimate the diameter of a suitable metal atom in the ground state and pursue a manufacturing procedure to excite alternate adjacent atoms to a very long metastable state, which is known to expand its size, much like Ryberg atoms. Hypothetically, this ideal situation would achieve a small difference in diameter of adjacent atoms sufficient to produce beat frequencies of resonant scattered ZPE.
Utilizing the Fermi-Thomas model of the atom, most atomic radii can be approximated by
a ≈ 1.4 ao / Z⅓ (22)
where Z = atomic number and ao = h2 / me2, the hydrogenic Bohr radius. Taking an excellent example of two atoms with similar size, platinum (Pt) and gold (Au) would be good candidates since they are next to each other on the periodic table and relatively inert, Noble metals. It is presumed that the diameter may resonate with a full wavelength, with 183 pm and 179 pm as the radii for Pt and Au respectively. In that case, 8.20 x 1017 Hz is the corresponding Pt frequency and 8.37 x 1017 Hz is the corresponding Au frequency, both in the soft X-ray band. Subtracting the two frequencies, the beat frequency would theoretically be a difference of 1.83 x 1016 Hz, moving it down into the UV band. If the conversion of UV incident electromagnetic energy is more efficient than transducing soft X-rays, then this method would offer a chance to collect ZPE, so long as the arrangement of multiple pairs of Pt and Au atoms could constructively interfere at their beat frequency. However, the wavelength of 1.83 x 1016 Hz is about 16 nm, which forces the placement of individual atomic pairs to be fairly distant from each other, compared to their size. With only a 2% difference in diameter, the beat frequency difference yields a power of ten difference for lower frequency detection, as the Mead-Cox resonant microsphere analysis of Figure 11. The improvement in amplitude from resonance would reasonably be only a power of two, unless a resonant cavity was used as well.
Another
example, representing the smallest atomic pair that is available for this
experiment, is hydrogen (H) and deuterium (D), an isotope of hydrogen
with one proton and one neutron in the nucleus. The Bohr radius ao for
hydrogen is 53 pm and the atomic radius of deuterium is about the same. In
fact, the Hα emission lines (Balmer series) for deuterium and
hydrogen are 656.10 nm and 656.28 nm respectively, a difference of only
0.03%.
Such a similar size will force the beating frequency to be more than a power of
ten difference, which apparently is viewed as an advantage by the patent
holders. For such gaseous atoms, the phenomenon of upscattering might
be achieved with this gas at a finite temperature T with a Maxwell-Boltzmann
velocity distribution if the incident ZPE virtual particles fell into a regime
of low energy up to about 10 kT.
This implies that it is possible for the incident particle to gain energy in a scattering collision.
In the situation where the hydrogen or deuterium nuclei might be at rest, the
scattering probability P(EI à Ef )
inversely depends upon the incident particle energy Ei. However, for
elastic scattering in a hydrogen (proton) gas, the scattering probability
depends on the final particle energy Ef and is not
zero even for Ef > Ei.
In Figure 24, a graph is shown of the scattering probability for scattering of
a proton gas with various incident particle energies. With resonance
considerations seen in Figure 25 added to the design as well, such a regime
might be a test, with a minimum of risk, for the Mead spherical collector
concept in an atomic, picosphere region. However, with or without a
successfully amplified beat frequency, the upscattering of virtual particles
from a proton gas may still have inherent flaws for two reasons: 1) most such
proton gas experiments have been conducted only with low ![]()
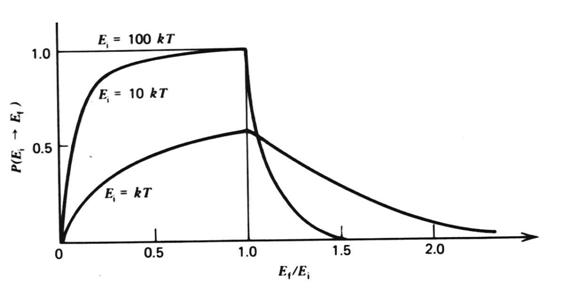
energy incident neutrons; 2) the dissipative effect of radiation reaction
precludes spontaneous absorption of energy from the vacuum field which normally
applies only to an atom in the ground state.
Yet, the gain of one to two times the incident EI = kBT
may be valuable to the energy equation as the gas transfers energy to the
incident particles, even if the probability drops to 50%, since theoretically
an abundant number of virtual particles are available. At room temperature (T
300K) for example, 1 kBT = 0.026 eV which is about 1013
Hz or an infrared terahertz frequency.

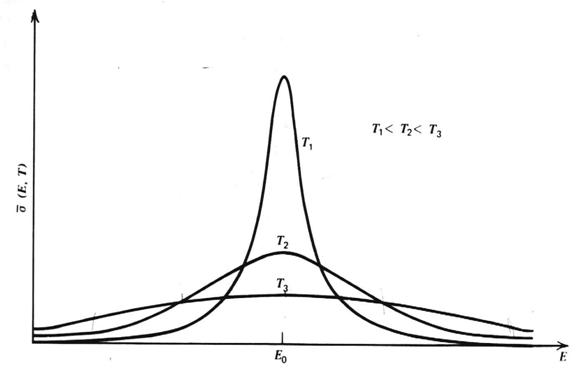
In Figure 25, an example of a capture resonance is shown at temperature T1,
where the average cross section dramatically increases for a certain resonant
incident energy Eo. Another aspect of temperature increase is also
graphically demonstrated. This is called Doppler broadening caused by the
Doppler shift in frequency as a thermally excited atom moves away from or
toward the incident particle with greater temperature-dependent speed.
Therefore, an increase in temperature causes the increased cross section of a
resonant peak to be lost. Lower temperatures are important for preserving the
advantage of resonance.
Thus examining the options for the resonant sphere, the two atomic pairs of deuterium and hydrogen are the best beating examples in the picosphere region, still demonstrating major unknowns in the beat frequency design concept of the Mead patent. At the present state of nanotechnology development however, the picospheres cannot be manufactured.
Quantum Femtosphere Amplifiers
With the examination of the femtosphere (R = 10-15 m = 1fm) there are a number of phenomena that synchronize so well with this dimension that the patent being examined seems to be more compatible with the nuclear particle than any other size sphere. The first obvious advantage is the spectral energy density of Equation (21) which is found to be 6.2 x 1035 J/m3 or 390 MeV/fm3. This is also interesting in that the quantum mechanical realm applies where hf is about the same as mc2. Testing for this condition, both energies are calculated with a wavelength of 2 x 10-15 m and a corresponding frequency (see Figure 22) of 1.5 x 1023 Hz. The Einstein formula for photon energy of the femtosphere is
E = hf = 9.9 x 10-11 J = 619 MeV . (23)
To determine the mass of the femtosphere, it is known that the radius of either the proton or neutron is about 8 x 10-16 m. , This is remarkably close (within 20%) to the conceptual femtosphere radius R of 1 fm. Therefore, it is reasonable to use the average mass of either nuclear particle (1.7 x 10-27 kg) in the Einstein equation for mass-energy, to find the energy equivalent of the femtospheres mass:
E = mc2 = 1.5 x 10-10 J = 938 MeV . (24)
Comparing Equations (23) and (24), they are the same order of magnitude, so it is determined that quantum mechanical rules apply in this region. The classical equations for energy and scattering cross section are still applicable. However, they may be regarded as classical approximations, in view of the correspondence principle, to quantum mechanical phenomena. The important quantum effects are (1) discreteness of the possible energy transfers, and (2) limitations due to the wave nature of the particles and the uncertainty principle.
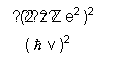 In
this femtosphere range, Rutherford scattering is applicable. The total nuclear
Rutherford scattering cross section is,
In
this femtosphere range, Rutherford scattering is applicable. The total nuclear
Rutherford scattering cross section is,
![]() σ = p
R2 (25)
where z is the number of charges (particles) in the incident at a velocity v
and Z is the number of charges (particles) in the target. For example, at high
velocities, even for incident virtual photon radiation, the total cross section
can be far smaller than the classical value of pR2, which is its
geometrical area.
The parenthetical terms in Equation (25) can result in a reduction of 10-24
times the geometrical area p
R2 of the target for an incident photon at the speed of light.
σ = p
R2 (25)
where z is the number of charges (particles) in the incident at a velocity v
and Z is the number of charges (particles) in the target. For example, at high
velocities, even for incident virtual photon radiation, the total cross section
can be far smaller than the classical value of pR2, which is its
geometrical area.
The parenthetical terms in Equation (25) can result in a reduction of 10-24
times the geometrical area p
R2 of the target for an incident photon at the speed of light.
For this size of target, due to vacuum polarization, it is important to mention that more incident virtual particles from the vacuum, as discussed in Chapter 1 (with an artist rendering in Figure 3), will also be present for a charged femtosphere. Therefore, the de Broglie wavelength of the incident particle will also be important, treating the ZPF virtual particles on the same level as electromagnetic waves:
λ = h/p = h/mv . (26)
The de Broglie requirement of quantum mechanics, postulated in 1924, thus affects the possibilities for energy generation for the Mead patented design. For a nucleus of finite sizethe de Broglie wavelength of the incident particle does enterThe situation is quite analogous to the diffraction of waves by a spherical object.
Vacuum polarization will also enhance the natural electromagnetic radiation from the vacuum for the femtosphere. Since double slit experiments with particles like electrons and neutrons demonstrate the wave phenomenon of diffraction, femtosphere particles can also be regarded as wave packets.
This type of scattering utilizes the continuously distributed energy eigenvalues of quantum mechanics which consider the boundary conditions at great distances from the collision. The scattering is treated here only as elastic scattering, so there is no absorption by the target. This is different from photoelectric scattering or Rayleigh scattering, which are inelastic.
For the region of λ > R this can be represented by the low energy limit where 2pR << λ (the circumference is much less than the wavelength). For the femtosphere, the total cross section is approximately σ ≈ 10-30 m2 in this low frequency, long wavelength region.
For the region of λ ≈ 2R or 2pR, there is a uniquely quantum mechanical phenomenon of resonant scattering called resonance fluorescence that applies to the absorption of radiation by an atom, molecule, or nucleus in a transition from its ground state to an excited state with the subsequent re-emission of the radiation in other directions in the process of de-excitation. The reaction of the target when the frequency of the incident equals the binding energy of the target, the scattering becomes very great, exhibiting a formal resonance peak seen in Figure 26.
 Note that a single femtosphere, such as a
free neutron or proton would not possess the requisite binding energy
for this type of oscillator resonance. In addition, this process reveals an inelastic
form of scattering but the dramatically increased cross section apparent in the
resonant
Note that a single femtosphere, such as a
free neutron or proton would not possess the requisite binding energy
for this type of oscillator resonance. In addition, this process reveals an inelastic
form of scattering but the dramatically increased cross section apparent in the
resonant
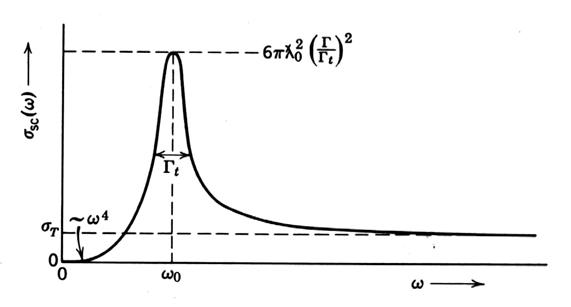
of
![]()
are seen in Figure 26, such as Thomson scattering, which is scattering of
radiation by a free charge. It can be X-rays by electrons or gamma rays
by a proton for example.
Thomson scattering occurs along a baseline of higher frequencies in Figure 26 above
ωo,
 where
the cross section is
where
the cross section is
![]()
σT = . (27)
The Thomson cross section of Equation (27), evaluated for a target electron, yields 6.6 x 10-25 cm2 for σT where e2/mc2 = 2.8 fm, the classical electron radius.
By comparison, the Rayleigh scattering (which causes the atmosphere to take on a blue color) cross section has a dependence on the fourth power of the incident frequency. Thus, the highest visible frequency (blue color) has a much larger scattering cross section and consequently, a stronger interaction with air molecules, including a wide scattering angle. Both phenomena illustrate the dominance of cross section scattering terms with cubic and quartic exponents.
Deuteron Femtosphere
One example of an intriguing femtosphere oscillator is the deuteron (a proton bound to a neutron in close contact), which also demonstrates resonant fluorescence. It would satisfy the requirement of binding energy for the target and is also treated as an oscillator. However, it should be mentioned that it is unlikely that the deuteron would exhibit beat phenomena, since the wave functions overlap making the deuteron behave as one nucleus (ionized deuterium), with a single resonant frequency and a radius of about 2 fm.
Recalling that the beat frequency design of the Mead patent is simply a means to downshift the radiated frequency, it is also possible to use the standard electrical engineering approach instead. Frequency converters, for example, utilize a local oscillator which mixes with the incoming signal to produce a subtracted intermediate frequency one or two orders of magnitude lower, for the same purpose. Once the resonant frequency of the deuteron is determined to be beyond the useful energy transduction range, an engineering recommendation therefore, would be to find a lower local oscillator in the same range, so that a substantially reduced intermediate frequency can be produced.
![]()
 The
deuteron has one bound state ( l = 0 ) of a proton and neutron with binding
energy of Eb = 2.23 MeV. The more preferred state ( 75% ) is where
the spin ½ of the proton and neutron are parallel (triplet state). The
cross section for the deuteron is σ = . (28)
The
deuteron has one bound state ( l = 0 ) of a proton and neutron with binding
energy of Eb = 2.23 MeV. The more preferred state ( 75% ) is where
the spin ½ of the proton and neutron are parallel (triplet state). The
cross section for the deuteron is σ = . (28)
Equation (28) is about 70 x 10-24 cm2 for the singlet (antiparallel) state and about 20 x 10-24 cm2 for the triplet state, which computes to 550 times and 157 times the geometrical cross sectional area, respectively.
With resonance fluorescence, the condition is in a sense an almost bound state that isnt below zero energy to be a true bound state (see the dashed line levels in Figure 27). If the potential V(r) is an attractive well, then the effective potential is,
Veff = V(r) + h2 l (l+1) / 2mr2 (29)
where the integer angular momentum quantum number, l >
1. Resonances are the bound states of the well at the positive energy,
indicated by the dotted linesWhat happens in scattering at a resonant energy
is that the incident 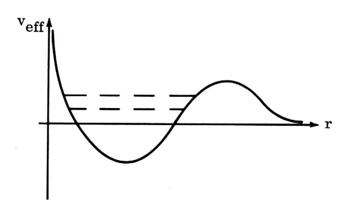 particle has a large probability of becoming
temporarily trapped in such a quasi-bound state of the well; this possibility
increases the scattering cross section.
In Figure 27, the depth of the
particle has a large probability of becoming
temporarily trapped in such a quasi-bound state of the well; this possibility
increases the scattering cross section.
In Figure 27, the depth of the  potential well for the deuteron must be Vo
= 36 MeV for the deuteron.
potential well for the deuteron must be Vo
= 36 MeV for the deuteron.
With that introduction to resonance with the deuteron, it should be mentioned that it is also an advantageous oscillator since the binding energy of Eb = 2.23 MeV corresponds to an X-ray frequency of fb = 5.4 x 1020 Hz, instead of the gamma ray frequency of 1023 Hz that should resonate with the diameter of a femtosphere. Thus, the deuteron binding energy satisfies the need for a lowering of the resonant frequency for transduction purposes, voiced in the Mead patent. The cross section is complicated by the existence of a singlet and triplet state depending on the proton and neutron spin direction. There are no bound excited states of the deuteron. Neutron-proton scattering experiments indicate that the force between n and p in the singlet state (antiparallel spins) is just sufficiently less strong than in the triplet state to make the deuteron unstable if the spins are antiparallelthere is a small, measurable quadrupole moment.
For the region of even smaller sizes, beyond the femtosphere resonance, where λ < R, the cross section can be represented by the high energy limit where R >> λ. Here the scattering by a perfectly rigid femtosphere can be approximated, as mentioned with the microsphere, with a total cross section of
σ ≈ 2 p R 2 (29)
which is twice the actual geometrical cross section area. The reason for the apparently anomalous result of Equation (29) is that the asymptotic form of the wave function is composed of the incident and the scattered wave, which also experiences interference between the two partial waves. However, so long as 2pR/λ is finite, diffraction around the sphere in the forward direction actually takes place, and the total measured cross sectionis approximately 2pR2.
Electron Femtosphere
The electron is the best femtosphere for many reasons. Its classical radius ro is calculated to be 2.8 x 1015 m or 2.8 fm and is suitable for a Mead patent test. As seen in Figure 3, the electron, like the proton, offers a steep electrical gradient at its boundary that creates a decay or polarization of the vacuum locally. It is expected that electron charge clusters like Cooper pairs or bigger boson charge bundles can offer a substantially enhanced vacuum activity in their vicinity. The patents of Ken Shoulders (US #5,018,180) and Hal Puthoff (US #5,208,844) on charge cluster devices discuss the potentials of such an approach but lack sufficient engineering feasibility to control their volatility. Therefore, an ion trap or force field confinement process is required.
QED vacuum effects such as the coupling of the atomic electron to the vacuum electromagnetic field show that the electron is more intimately connected to the vacuum flux than most other particles. The zero-point oscillations of the field contribute to the electron a certain amount of energyEfl ~ e2h/4mca2, with an upper bound of hfmax = 15 MeV for a free electron. The coupling term for the atomic electron in the Hamiltonian is (e2/2mc2 )A2 where A is the vector potential and the parenthetical modifier is familiar from Equation (27) as half of the classical electron radius. Since this term does not involve atomic operators, it contributes the same energy to every state in the atom. Besides the ground state contribution, called the Lamb shift, it appears that every other electron level is also shifted upwards from vacuum flux energy or virtual particles. For this reason alone, it should be emphasized that extraction of energy from the vacuum is already occurring in every atom throughout the universe, since every atomic electron and every free electron is positively energized. However within the atomic system, the effects of the vacuum field and radiation reaction cancel, so that the spontaneous absorption rate is
A12 = RVF - RRR = ½ A21 - ½ A21 = 0 (30)
where A12 is the Einstein A coefficient for the electron transition from the ground state to the first atomic energy level. The spontaneous emission rate sums the rate of energy absorption from the vacuum field RVF and the radiation reaction rate RRR to equal the Einstein A coefficient.
The
energetic scattering of the vacuum flux on a free electron, clearly seen in
Figure 3, may perhaps be optimally amplified in the gas state, such as within
the confines of an ion trap. This author collaborated in the
construction of such a trap, which proved that electron and ion densities can
be increased with such a trap, as the electrons are retained in one place for
measurements and 
energy extraction.
Such an apparatus may also work well for charge clusters,  after applying inductive braking to their
kinetic energy. For an applied voltage of 300V and vacuum pressures of at least
a microTorr, the concentration of ions
after applying inductive braking to their
kinetic energy. For an applied voltage of 300V and vacuum pressures of at least
a microTorr, the concentration of ions  ranged between 108 and 1010
ions per cc. As seen in Figure 29, the voltage profile or potential
distribution inside the grid with the presence of negative space charge from
the Thoriated filaments exhibits a large concentration of electrons. Assuming
that charge clusters cannot be trapped by any other means without
ranged between 108 and 1010
ions per cc. As seen in Figure 29, the voltage profile or potential
distribution inside the grid with the presence of negative space charge from
the Thoriated filaments exhibits a large concentration of electrons. Assuming
that charge clusters cannot be trapped by any other means without
![]()
destroying them, the nonresonant ion trap should provide a reliable method for
study and possible energy extraction if an additional collection and
amplification method for the femtosphere is optimized and implemented.
Weisskopf notes that if the electron is assumed to be a sphere of radius a, then only waves with a wavelength λ /2p > a will act upon the electron, while the wavelengths λ /2p >> a will not be that significant. The upper bound of hfmax assumes an electron radius of a = c/fmax while the number of vibration modes of the ZPF gives rise to a value of a ≈ ro( hc/e2)½ so that the fluctuation energy seemingly pushes the electron radius to even greater values
Casimir Force Electricity Generator
A fascinating example of utilizing mechanical forces from the Casimir effect and a change of the surface dielectric properties, to intimately control the abundance of virtual particles, is an optically-controlled vacuum energy transducer developed by a Jet Propulsion Lab scientist. A moving cantilever or membrane is proposed to cyclically change the active volume of the chamber as it generates electricity with a thermodynamic engine cycle. The invention proposes to use the Casimir force to power the microcantilever beam produced with standard micromachining technology. The silicon structure may also include a microbridge or micromembrane instead, all of which have a natural oscillation frequency on the order of a free-carrier lifetime in the same material. The discussion will refer the (micro)cantilever design but it is understood that a microbridge or flexible membrane could also be substituted. The invention is based on the cyclic manipulation of the dimensions of Casimir cavity created between the cantilever and the substrate as seen in Figure 30. The semiconducting membrane (SCM) is the cantilever which could be on the order of 50-100 microns in size with a few micron thickness in order to obtain a resonant frequency in the range of 10 kHz, for example.

 Two monochromatic lasers (RS) are turned on
thereby increasing the Casimir force by optically changing the dielectric properties
of the cantilever. This frequency dependence of a dielectric constant, can be
seen in Figure 15. It can vary with frequency by a few orders of magnitude
inversely proportional to the frequency. The standard analysis of cavity modes
usually identifies the resonant modes of the cavity, dependent on the boundary
conditions. ,
However, Pintos pro-active approach is to excite a particular frequency mode
in the cavity. In doing so, an applied electrostatic charge (Vb)
increases as the cantilever is pulled toward the adjacent substrate (SCP) by
the Casimir force. Bending the charged
cantilever on a nanoscale, the Casimir attractive force is theoretically
balanced with opposing electrostatic forces, in the same way as Forwards
parking ramp of Figure 8. As the potential difference to the cantilever
assembly is applied with reference to a conducting surface (CP2) nearby, the
distance to this surface is also kept much larger than the distance between the
cantilever and the substrate (SCP). Upon microlaser illumination, which changes
the dielectric properties of the surface and increases the Casimir force, there
is also predicted an increase in electrostatic energy due to an increase in
capacitance and voltage potential. Therefore a finite electrical current can be
extracted and the circuit battery is charged by an energy amount equal to the
net work done by the Casimir force. Pinto estimates the Casimir force field
energy transfer to be approximately 100 to 1000 erg/cm2.
Converting this to similar units used previously, this Casimir engine should
produce in the range of 60 to 600 TeV/cm2 (teraelectron volts per
square centimeter) which is also equal to 0.01 to 0.1 mJ/cm2
for every cycle in Figure 31.
Two monochromatic lasers (RS) are turned on
thereby increasing the Casimir force by optically changing the dielectric properties
of the cantilever. This frequency dependence of a dielectric constant, can be
seen in Figure 15. It can vary with frequency by a few orders of magnitude
inversely proportional to the frequency. The standard analysis of cavity modes
usually identifies the resonant modes of the cavity, dependent on the boundary
conditions. ,
However, Pintos pro-active approach is to excite a particular frequency mode
in the cavity. In doing so, an applied electrostatic charge (Vb)
increases as the cantilever is pulled toward the adjacent substrate (SCP) by
the Casimir force. Bending the charged
cantilever on a nanoscale, the Casimir attractive force is theoretically
balanced with opposing electrostatic forces, in the same way as Forwards
parking ramp of Figure 8. As the potential difference to the cantilever
assembly is applied with reference to a conducting surface (CP2) nearby, the
distance to this surface is also kept much larger than the distance between the
cantilever and the substrate (SCP). Upon microlaser illumination, which changes
the dielectric properties of the surface and increases the Casimir force, there
is also predicted an increase in electrostatic energy due to an increase in
capacitance and voltage potential. Therefore a finite electrical current can be
extracted and the circuit battery is charged by an energy amount equal to the
net work done by the Casimir force. Pinto estimates the Casimir force field
energy transfer to be approximately 100 to 1000 erg/cm2.
Converting this to similar units used previously, this Casimir engine should
produce in the range of 60 to 600 TeV/cm2 (teraelectron volts per
square centimeter) which is also equal to 0.01 to 0.1 mJ/cm2
for every cycle in Figure 31.
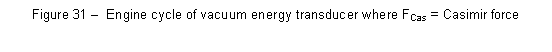
Analysis of the Casimir engine cycle demonstrates its departure from
hydroelectric, gaseous, or gravitational systems. For example, the Casimir
pressure always acts opposite to the gas pressure of classical
thermodynamics and the energy transfer which causes dielectric surface changes
does not flow to the virtual photon gas.
Altering physical parameters of the device therefore, can change the total work
done by the Casimir force, in contrast to gravitational or hydroelectric
systems. Unique to the quantum world, the type of surface and its
variation with optical irradiation is a key to the transducer operation.
Normally, changing the reflectivity of a surface will affect the radiation
pressure on the surface but not the energy density of the real photons.
However, in the Casimir force case, Pinto explains, the normalized energy
density of the radiation field of virtual photons is drastically affected by
the dielectric properties of all media involved via the source-free Maxwell
equations.
Specifically, Pinto discovered that the absolute value of the vacuum energy can change just by causing energy to flow from a location to another inside the volume V. This finding predicts a major breakthrough in utilization of a quantum principle to create a transducer of vacuum energy. Some concerns are usually raised, as mentioned previously, with whether the vacuum energy is conserved. In quantum systems, if the parameters (boundary conditions) are held constant, the Casimir force is strictly conservative in the classical sense, according to Pinto. When they are changed, however, it is possible to identify closed paths along which the total work done by this force does not vanish.
To conclude the energy production analysis, it is noted by Pinto that 10,000 cycles per second are taken as a performance limit. Taking the lower estimate of 100 erg/cm2 per cycle, power or wattage is calculated to be about 1 kW/m2 which is on par with photovoltaic energy production. However, on the scale of interest, where s in Figure 31 is always less than 1 μm, the single cantilever transducer is expected to produce about 0.5 nW and establish a millivolt across a kilohm load, which is still fairly robust for such a tiny machine.
The basis of the dielectric formula starts with Pintos analysis that the Drude model of electrical conductivity is dependent on the mean electron energy <E> (less than hf) and estimated to be in the range of submillimeter wavelengths. The Drude model, though classical in nature, is often used for comparison purposes in Casimir calculations. The detailed analysis by Pinto shows that carrier concentrations and resistivity contribute to the estimate of the total dielectric permittivity function value, which is frequency dependent. The frequency dependence is of increasing concern for investigations into the Casimir effects on dielectrics.
Analyzing the invention for engineering considerations, it is clear that some of the nanotechnology necessary for fabrication of the invention have only become available very recently. The one-atom microlaser, invented in 1994, should be a key component for this invention since about ten photons are emitted per atom. However, it has been found that new phenomena, (1) the virtual-photon tunnel effect and (2) the virtual-photon quantum noise, both have an adverse effect on the preparation of a pure photon-number state inside a cavity, which may impede the performance of the microlaser if placed inside a cavity. Pinto concurs that such a low emission rate is necessary since the lasing must take place as a succession of very small changes
![]()

Another suggested improvement to the original invention could involve a
femtosecond or attosecond pulse from a disk-shaped semiconductor microlaser
(such as those developed by Bell Laboratories). The microlaser could be used in
close proximity to the cantilever assembly. Such microlaser structures, called
microdisk lasers measuring 2 microns across and 100 nm thick, have been shown
to produce coherent light radially (see Figure 32). A proper choice of laser
frequency would be to tune it to the impurity ionization energy of the
semiconductor cantilever. In this example, the size would be approximately
correct for the micron-sized Casimir cavity.
Pinto chooses to neglect any temperature effects on the dielectric permittivity. However, since then, the effect of finite temperature has been found to be intimately related to the cavity edge choices that can cause the Casimir energy to be positive or negative. Therefore, the contribution of temperature variance and optimization of the operating temperature seems to have become a parameter that should not be ignored. Also supporting this view is the evidence that the dielectric permittivity has been found to depend on the derivative of the dielectric permittivity with respect to temperature.
Cavity QED Controls Vacuum Fluctuations
It is known from the basic physics of cavity QED that just the presence of the walls of a cavity will cause any atoms within it to react differently. For example, the spontaneous emission rate at wavelength should be completely suppressed if the transition dipole moment is parallel to the mirror plates where the walls of the cavity are reflecting conductors. In other words, a confined antenna cannot broadcast at long wavelengths. An excited atom in a small cavity is precisely such an antenna, albeit a microscopic one. If the cavity is small enough, the atom will be unable to radiate because the wavelength of the oscillating field it would like to produce cannot fit within the boundaries. As long as the atom cannot emit a photon, it must remain in the same energy level; the excited state acquires an infinite lifetime[because] there are no vacuum fluctuations to stimulate its emission by oscillating in phase with it. Such effects are noticed for cavities on the order of hundreds of microns and smaller, precisely the range of Pintos cavity. Therefore, it can be expected that carefully choosing the fundamental resonant frequency of the cavity will provoke the emission of photons so that the dielectric effect on the walls may be enhanced with less input of energy.
Furthermore, the most important Casimir force research relating to Pintos invention may be the analysis of a vibrating cavity. If the membrane oscillation frequency is chosen, for example, to be close to a multiple frequency (harmonic) of the fundamental unperturbed field mode of the cavity, resonant photon generation will also provoked. Such resonant photon generation in a vibrating cavity like Pintos has been studied in the literature. ,
Another aspect of the Pinto experiment apparently not discussed in his article is the relative concentration of gas molecules in the vacuum energy transducer of Figure 30. Though a complete evacuation of air would be preferable, especially when compression of the membrane could be impeded by increasing gas pressures, it is naturally expected that too many gas molecules will still remain airborne even with a high vacuum, such as 10-10 to 10-12 Torr. Therefore, using another characteristic of cavity QED may be recommended. First of all, the selection of the gas is important, so that the atomic transition frequency matches the cavity resonant frequency very closely. Once this is achieved, it would be recommended, from an engineering point of view, to optimize the design of the size of the cavity transducer so that the atomic transition has a slightly higher frequency than the resonant frequency of the cavity. This could easily occur with the resonant wavelength slightly longer than the resonant transition wavelength of the gas in question. In that way, the gas molecules will be repulsed from entering the cavity, thus creating a lower gas pressure inside. Logically, this would be accomplished with the cavity transducer in the maximum SA position in Figure 30. It would thereby add to the compression force of the movable membrane. As the membrane reaches its lowest position in the engine cycle with minimum SA position, cavity QED dictates that since the atomic transition frequency will then be lower than the resonant frequency of the cavity, the force will be attractive, pulling gas molecules toward the cavity and increasing the pressure. This condition may be accomplished as well, since the shorter wavelength of the smaller cavity size will now be less than the longer wavelength of the atomic transition wavelength of the gas. Such a condition, with extra gas molecules in the cavity, will assist in pushing the membrane upwards again. Such detailed planning with gases and cavity dimensions should create a situation where the ZPF is supplying a larger percentage of the energy output, with a minimum of nanolaser input energy. If so, the Pinto vacuum energy generator would offer an unparalleled miniature electricity source that could fill a wide range of nanotechnology needs and microelectronic needs.
Spatial Squeezing of the Vacuum
The analysis of Pintos
invention is analogous to spatial squeezing of the initial states to decrease
the energy density on one side of a surface, below its vacuum value, in order
to increase the Casimir force. For an oscillating boundary like Pintos, this
can also create a correlated excitation of frequency modes into squeezed states
and sub-Casimir regions ![]() where
the vacuum develops structure. Pressing zero-point energy out of a spatial
region can be used to temporarily increase the Casimir force.
This spatial squeezing technique is gaining increasing acceptance in the
physics literature as a method for bending quantum rules while gaining a
short-term benefit, such as modulating the quantum fluctuations of atomic
displacements below the zero-point quantum noise level of coherent phonon
(vibrational) states, based on phonon-phonon interactions.
where
the vacuum develops structure. Pressing zero-point energy out of a spatial
region can be used to temporarily increase the Casimir force.
This spatial squeezing technique is gaining increasing acceptance in the
physics literature as a method for bending quantum rules while gaining a
short-term benefit, such as modulating the quantum fluctuations of atomic
displacements below the zero-point quantum noise level of coherent phonon
(vibrational) states, based on phonon-phonon interactions.
 The squeezing technique involves minimizing
the expectation value of the energy in a prescribed region, such as a cavity.
In general, a squeezed state is obtained from an eigenstate of the
annihilation operatorby applying to it the unitary squeezing (or dilation)
operator.
Ideally, it seems promising to generate squeezed modes inside a cavity by an
instant change of length of the cavity.
The implied infinite speed or frequency for a movable membrane would not be
achievable however. If it were approachable, the squeezing would cause a
modification of the Casimir force so that it could become a time dependent
oscillation from a maximum to minimum force. Pursuing resonance measurements
may turn out to be the most realistic experimental approach in order to exploit
the periodic variation in the Casimir force by squeezing.
The squeezing technique involves minimizing
the expectation value of the energy in a prescribed region, such as a cavity.
In general, a squeezed state is obtained from an eigenstate of the
annihilation operatorby applying to it the unitary squeezing (or dilation)
operator.
Ideally, it seems promising to generate squeezed modes inside a cavity by an
instant change of length of the cavity.
The implied infinite speed or frequency for a movable membrane would not be
achievable however. If it were approachable, the squeezing would cause a
modification of the Casimir force so that it could become a time dependent
oscillation from a maximum to minimum force. Pursuing resonance measurements
may turn out to be the most realistic experimental approach in order to exploit
the periodic variation in the Casimir force by squeezing.
In Figure 33, the effect of squeezing can be seen in the fundamental cavity mode n = 0 where the emission of photons is almost double that allowed by the Planck radiation law Equation (9), where there are quantized field modes. Hu found that the other field modes go to a mixed quantum state due to the intermode interaction caused by the classical Doppler effect from the moving mirrors. The theory also predicts that the significant features of the nonstationary Casimir effect are not sensitive to temperature.
![]()
 Focusing
Vacuum Fluctuations
Focusing
Vacuum Fluctuations
Another development that may directly affect transduction possibilities of ZPE is the theoretical prediction of focusing vacuum fluctuations. Utilizing a parabolic mirror designed to be about 1 micron in size (labeled a in Figure 33), with a plasma frequency in the range of 0.1 micron for most metals, Ford predicts that it may be possible to deflect atoms with room temperatures of 300K, levitate them in a gravitational field, and trap them within a few microns of the focus F. A positive energy density results in an attractive force. Depending upon the parameters, it may alternatively result in a repulsive Van der Waals force at the focus with a region of negative energy density. This type of trapping would require no externally applied electromagnetic fields or photons. The enhanced vacuum fluctuations responsible for these effects are found to arise from an interference term between different reflected rays. The interesting conundrum is the suggestion that parabolic mirrors can focus something even in the absence of incoming light, but vacuum fluctuations are often treated as evanescent electromagnetic fields. The manifestation of the focusing phenomenon is the growth in the energy density and the mean squared electric field near the focus.
Focusing vacuum fluctuations in many ways resembles amplified spontaneous emission (ASE) which occurs in a gain medium, where the buildup of intensity depends upon the quantum noise associated with the vacuum field.
![]()
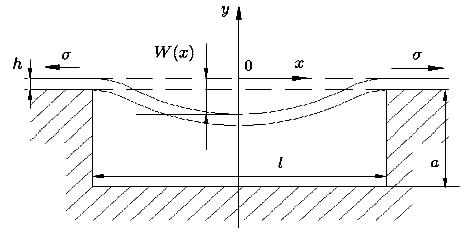
Stress Enhances Casimir Deflection
An interesting Casimir force effect, seen more and more frequently in nano-electromechanical system (NEMS), is illustrated in Figure 35. Shown is a membrane or cantilever of thickness h that covers a well of width l and height a, which is deflected in the y direction, by an amount of distance W(x) depending upon the position with respect to x. The equation describing the deflection of any point on the membrane is:
D ∂4W(x)/ ∂x4 = F . (31)
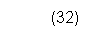
 D
= Eh3/(12-12p2) where E is the elastic modulus, h is the
thickness (see Figure 35) of the membrane, and p is the Poisson ratio. The
Poisson ratio is the ratio of the transverse contracting strain to the
elongation strain.
The Casimir force F in Equation (31), due to the proximity to the bottom plate,
is an inhomogeneous force in this situation, varying from point to point along
x as
D
= Eh3/(12-12p2) where E is the elastic modulus, h is the
thickness (see Figure 35) of the membrane, and p is the Poisson ratio. The
Poisson ratio is the ratio of the transverse contracting strain to the
elongation strain.
The Casimir force F in Equation (31), due to the proximity to the bottom plate,
is an inhomogeneous force in this situation, varying from point to point along
x as
![]()
F =
where h, W(x) and a are defined above.
Equations (31) and (32) are then equated to produce a quartic equation dependent on W(x) where the residual applied stress/strain σ can be added as a modifier. Solving for W(x) under conditions of strain (stretching) yields a tendency toward a stationary wave pattern characteristic of buckling, without any appreciable change in the center deflection. Solving for W(x) under conditions of stress (compression) reveals that compressive residual stress enhances the deflection of the bridge and reduces its [buckling] behaviour. The amount of enhancement at the center is W(0) = 0.0074a or almost 1%. However, since the Casimir force in Equation (32) increases by the fourth power of the distance (a W(x)), it is also regarded as a positive feedback system, with a tendency of increasing any deflection in a direction toward structural failure.
Casimir Force Geometry Design
Since the Casimir force is such an integral part of the experimental energy manifestations of the ZPF as well as the Chapter 4 analysis, it is worthwhile to review some of its important characteristics. First of all, the attractive Casimir force between two uniform, flat metal plates which are perfectly conducting (and therefore, a reflective surface) is
F = p2 hc / 240 d4 (33)
where d is the spacing between the plates. Milonni points out that besides the usual vacuum fluctuations approach, one can also treat the virtual photons of the vacuum as carriers of linear momentum. This perspective yields a mathematical proof that the Casimir force can also be classically analyzed as a physical difference of radiation pressure on the two sides of each plate.
In comparison, the Coulomb force for charged plates, such as with Forwards charge foliated conductors of Figure 8, is found to be
FCoul = V2 / 8pd2 . (34)

Thus, with a potential difference of only V = 17 mV at d = 1 μm, the
Casimir force equals the Coulomb force.
This is also the operating principle behind Pintos cavity transducer of Figure
30, as the Casimir force is varied cyclically.
In Figure 36, a comprehensive approach by Maclay is made for an arbitrarily-sized box made of perfectly conducting surfaces. As the dimensions of the box deviate from a cubic design (1 x 1 x 1) the Casimir forces change as well.

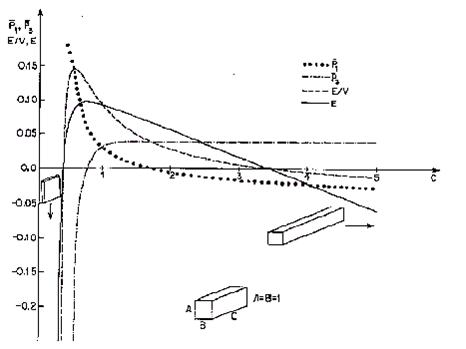
A maximum positive energy density (dark area near the origin) signifies a positive Casimir force or outward pressure. Effectively, positive energy density produces a repulsive Casimir force. The dimensions of 1 x 1 x 1.7 signify the transition zone known as zero energy density. Any further increase in size results in a negative or attractive Casimir force. It is readily apparent from these calculations that a similar system, with a movable membrane like Pintos Figure 30, offers a restoring force for either deviation from zero, as if the cavity held a compressible fluid.
In Figure 37, the Casimir forces for a perfectly conducting 1 x 1 x C rectangular box, expanding from C = 1 to an elongated size, can be traced quite closely. Again, as in Figure 36, it can be seen that as C = 1.7 the Casimir pressure P1 crosses the zero energy line. To help distinguish the Casimir energy density E / V and Casimir energy E lines from the rest, it is noted that these two lines cross zero at the same point C = 3.5, while the Casimir pressure P3 line stays constant past C = 1. The E / V, E, and P3 lines are all negative when C < 1 showing the dominance of d4 in the denominator of Equation (33), when two surfaces approach 1 micron or less.
The discovery by Maclay of a particular box dimension (1 x 1 x 1.7), that sits in the middle of attractive and repulsive Casimir forces, presents a possible scenario for vacuum energy extraction. This interesting motion suggests that we may be organizing the random fluctuation of the EM field in such a way that changes in pressure directly result, which could lead to work being done. One interesting question is can we design a cavity that will just oscillate by itself in a vacuum. One approach to this would require a set of cavity dimensions such that the force on a particular side is zero, but if the side is moved inward, a restoring force would be created that would tend to push it outward, and vice versa. Hence a condition for oscillation would be obtained. Ideally, one would try to choose a mechanical resonance condition that would match the vacuum force resonance frequency. More complex patterns of oscillation might be possible. The cavity resonator might be used to convert vacuum fluctuation energy into kinetic energy or thermal energy. More calculations of forces within cavities are needed to determine if this is possible, what would be a suitable geometry and how the energy balance would be obtained. Maclay concedes however, that upon analyzing Forwards charged parking ramp of Figure 8, with like charges supplying the restorative force to the Casimir attractive force, that no net work would be done for any given oscillation cycle.
When dielectrics are considered, the analysis becomes more involved. Calculations of Casimir forces for situations more complicated than two parallel plates are notoriously difficult, and one has little intuition even as to whether the force should be attractive or repulsive for any given geometry. With a dielectric set of parallel plates, the characteristics of dispersive (phase velocity is a function of frequency) or non-dispersive (all frequencies equally transmitted or reflected) dielectrics enters into the equation. For example, a classic example is two dispersive dielectric parallel plates that have a Casimir energy which depends only on the distance between the plates and the dispersion of the dielectrics.
![]()
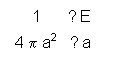 Various geometries of rectangular cavities
can also be studied using the principle of virtual work where E = - ∫ F
dx. With the Casimir vacuum energy E for
a dielectric ball of radius a, for example, the Casimir force per unit area is,
Various geometries of rectangular cavities
can also be studied using the principle of virtual work where E = - ∫ F
dx. With the Casimir vacuum energy E for
a dielectric ball of radius a, for example, the Casimir force per unit area is,
![]()
F =
For a dilute, dispersive dielectric ball for example, the Casimir surface force is found to be attractive with inward pressure. A system of two dielectric spheres with general permittivities and some chosen values of the refractive index n has also been evaluated for Casimir forces.
![]()
 One
application for this type of Casimir force calculation lies with biological
cells which are spheres with a high dielectric constant. Figure 38 shows a
B-lymphocyte which is 1 micron across which therefore must experience
and compensate for the inward Casimir pressure. Biological structures may also
interact with the vacuum field. It seems possible that cells, and components of
cells, for example, the endoplasmic reticulum may interact with the vacuum
field in specific ways. A cell membrane, with a controllable ionic
permeability, might change shape in such a way that vacuum energy is
transferred. Microtubules, in cell cytoskeletons, may have certain specific properties
with regard to the vacuum field. Diatoms, with their ornate geometrical
structures, must create interesting vacuum field densities; one wonders if
there is a function for such fields.
Many of these structures that are less than one micron in size have much higher
Casimir pressures to contend with, such as ribosomes which are about 0.02
micron across.
One
application for this type of Casimir force calculation lies with biological
cells which are spheres with a high dielectric constant. Figure 38 shows a
B-lymphocyte which is 1 micron across which therefore must experience
and compensate for the inward Casimir pressure. Biological structures may also
interact with the vacuum field. It seems possible that cells, and components of
cells, for example, the endoplasmic reticulum may interact with the vacuum
field in specific ways. A cell membrane, with a controllable ionic
permeability, might change shape in such a way that vacuum energy is
transferred. Microtubules, in cell cytoskeletons, may have certain specific properties
with regard to the vacuum field. Diatoms, with their ornate geometrical
structures, must create interesting vacuum field densities; one wonders if
there is a function for such fields.
Many of these structures that are less than one micron in size have much higher
Casimir pressures to contend with, such as ribosomes which are about 0.02
micron across.
Other geometrical objects have also been analyzed for the resultant Casimir forces such as hemispheres, pistons, and flat, circular disks. Instead of solid objects, configurations such as spherically symmetric cavities have also been presented in the literature. Rectangular cavities, for example, have also been found to have a temperature dependence and edge design variations which can lead to the Casimir energy being positive or negative.
Another interesting area of possible energy extraction from the Casimir effect is in astronomical bodies such as stars. The Casimir effect has been proposed as a source of cosmic energy. In such cosmological objects as white dwarfs, neutron stars, and quasars, the volume effect of the Casimir force is theoretically sufficient to explain the huge output of quasars for example. A calculation of the shift in energy density of the ZPF due to the presence of an ideal conductor in a volume V of space relative to the case with an absence of the volume is the mean value of the stress-energy tensor of QED inside volume V. A conductive material will be conductive for frequencies below the plasma frequency ω < ωp and transparent for frequencies above the plasma frequency ω > ωp. The plasma frequency, for nonpropagating oscillations depending only on the total number of electrons per unit volume is, in Gaussian units,
ωp2 = 4p ne2 / m . (36)
The dielectric constant for high frequencies is also dependent on the plasma frequency (compare with Figure 15),
ε (ω ) = 1 ωp2 / ω2 . (37)
(In dielectric media, Equation (37) applies for ω2 >> ωp2.) The shift in the vacuum energy density due to the presence of a volume of ideal conducting material is, expressed in terms of the plasma frequency,
Δ Evac = ωp4 h c / 4p2 . (38)
With a dramatic increase in the electron density n due to gravitational compression in collapsing stars, an energy creation is predicted that compares with 1038 J expected for a nova or 1042 J for a supernova if the radius of the star is compressed to approximately R ≈ 107 m.
Vibrating Cavity Photon Emission
Various cavities have been analyzed so far for the net Casimir effect. However, the case of photon creation from the vacuum due to a non-stationary Casimir effect in a cavity with vibrating wall(s) is unique and has interesting ramifications. Comparing with Pintos cavity of Figure 30, the cavity chosen by Dodonov to create resonance photon generation also has one moving wall while the rest of the rectangular cavity is stationary. The fundamental electromagnetic mode is ω1 = p c / Lo where Lo is the mean distance between the walls of the cavity. The maximum value of the energy is found to be three times the minimum value, depending on the phase. The total energy also oscillates in time and the photon generation rate tends toward a constant value as long as any detuning is less than one.
While changes in the dielectric constant of cavity walls affect the Casimir vacuum force of Pintos vibrating cavity, there are also effects from a change in the refractive index of a medium. Hizhnyakov presents evidence for the emission of photons from such a distortion of the spectrum of zero point quantum fluctuations. If the medium experiences a time-dependent refractive index, it has been demonstrated that part of the energy will be emitted as real photons. An example is a dielectric medium excited by a rectangular light pulse for about a femtosecond (10-15 seconds). The spectral density of the photon energy is shown to depend only upon the rate of change of the refractive index over time, which is unusual. While Hawking and Unruh radiation effects are mixed thermal states, this refractive index derivative effect is said by Hizhnyakov to be a pure state equally related to the ZPF as a non-linear quantum optical effect. In terms of energy flow, a picojoule (10-9 J) laser pulse lasting for a femtosecond produces about ten megawatts (10 MW/cm2) of power input and the input pulse has about 10-5 cm2 cross sectional area which gives about a 100 W power input. The output intensity, estimated to be about a picowatt, is calculated to be the sum of two pulses created from the leading and trailing edges of the input refractive index change.
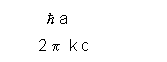 The Unruh radiation referred to
above is actually called the Unruh-Davies effect which refers to a phenomenon
related to uniform acceleration. In a scalar field such as the ZPE vacuum, the
effect of acceleration is to promote zero-point quantum field fluctuations to
the level of thermal fluctuations.
Milonni points out that it took a half a century after the birth of quantum
theory for the thermal effect of uniform acceleration to be discovered. The
effective temperature that would be measured by an accelerated detector in a
vacuum is
The Unruh radiation referred to
above is actually called the Unruh-Davies effect which refers to a phenomenon
related to uniform acceleration. In a scalar field such as the ZPE vacuum, the
effect of acceleration is to promote zero-point quantum field fluctuations to
the level of thermal fluctuations.
Milonni points out that it took a half a century after the birth of quantum
theory for the thermal effect of uniform acceleration to be discovered. The
effective temperature that would be measured by an accelerated detector in a
vacuum is
![]()
TU =
which leads to the interpretation that thermal radiation is very similar to vacuum fluctuation radiation. In Equation (38), k is the wave number (ω/c) and a is the acceleration. Both vacuum probability distribution functions and thermal distributions exhibit a Gaussian probability distribution since the vacuum distribution is the T à 0 limit of the thermal distribution.
Looking at Hawking radiation, which is emitted from a black hole, it is based on the premise that pair production from the vacuum can occur anywhere, even at the event horizon of a black hole. The treatment is related to a mathematical manipulation called Wick rotation, where the metric is rotated into the complex plane with time t à - i t, so that the temperature is inversely equal to the period. Solving for the region just outside the event horizon r > 2GM, where G is the gravitational constant, the Hawking temperature is found to be
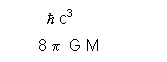
![]()
TH =
where M is the mass of the black hole. Since Plancks constant is included in Equation (39), Zee notes that Hawking radiation is indeed a quantum effect. The similarities between Equations (38) and (39) are referred to by Hizhnyakov.
Fluid Dynamics of the Quantum Vacuum
In the analysis of Figure 37, it was mentioned that the Casimir force within cavities of Pinto and Maclay, possessing one movable wall, behave like a compressible fluid since a restoring force is present for any deviation from the zero-force position. It turns out that more exact analogies to fluids are possible for the quantum vacuum. A hydrodynamic model of a fluid with irregular fluctuations has been proposed by Bohm and Vigier for the vacuum, which also satisfies Einsteins desire for a causal interpretation of quantum mechanics. Their work also includes a proof that the wave function probability density P = |ψ|2 used in quantum theory approaches the standard formula for fluid density with random fluctuations. There is also a suggestion of further work regarding how a fluid vortex provides a very natural model of the non-relativistic wave equation of a particle with spin.

A computational fluid dynamics
approach to the ZPF, with the ambitious aim of reducing flight resistance at
superluminal speeds has been proposed by Froning and Roach.
The negative energy density region seen in Figure 37 between Casimir plates is
also implicated in spacetime warping concepts and a theoretical increase in the
speed of light. Resistance to flight in air and space have interesting
parallels in this theory. In Figure 39, the aerodynamic viscous drag resistance
to increased speed is compared to the electromagnetic zero-point vacuum
resistance to increased speed, which is perceived as inertia. Drawing upon the
separate works by Puthoff and Haisch (cited in Chapter 2), this 
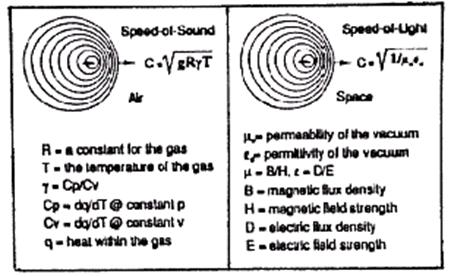
approach takes their ZPE-related gravity and inertia theory to the engineering
level of experimental simulation. In Figure 40, the analogy is drawn between
the well-known equation for the speed of
light c = ( μoεo
)-½ and the aerodynamic gas equation for the speed of
sound c = (gRγT)-½
with compressible fluid graphics for each. The aerodynamic resistance of
viscous drag exerted on the substructure of a vehicle is compared to the
Lorentz force exerted on the substructure of the vehicle by the ZPF, which is
also proposed to be a Casimir-like force exerted on the exterior by unbalanced
ZPE radiation pressures. The conclusion drawn from this first-order analysis is
that μo and εo
can be perturbed by propagation speed and possibly vehicle inertia, accompanied
by a distortion of the zero-point vacuum.
A
fundamental part of the Fronig and Roach approach to the fluid dynamic
simulation of superluminal speeds is the proposal that μo and εo can be reduced
significantly by nonabelian electromagnetic fields of SU(2) symmetry. It is
proposed that EM fields of nonabelian form have the same symmetry that
underlies gravity and inertia. Their approach is particularly to use alternating
current toroids with resonant frequencies. That nonabelian gauge symmetry
offers a higher order of symmetry has been seen elsewhere in the literature.
Zee, for example, notes that the square of the vector potential A2
would normally be equal to zero in the abelian gauge, which all standard
(trivial) electromagnetic theory texts use. Instead, he notes that a field
strength such as F = dA + A2 can be formulated easily in the
nonabelian gauge and shown to be nonzero and gauge covariant (though not invariant).
Furthermore, the nonabelian analog of the Maxwell Langrangian, called the
Yang-Mills Langrangian, includes cubic and quartic terms that describe
self-interaction of nonabelian bosons (photons), as 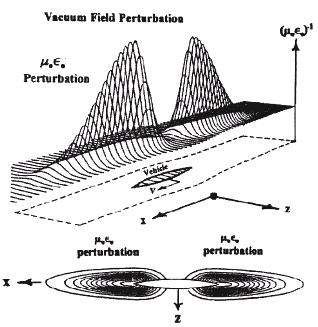 well as a nonabelian Berrys phase that is
intimately related to the Aharonov-Bohm phase. (The Aharonov-Bohm phase depends
exclusively on the vector potential.) Even the strong nuclear interaction is
accurately described by a nonabelian gauge theory. Pure Maxwell theory is free
and so essentially trivial. It contains a noninteracting photon. In contrast,
pure Yang-Mills theory
well as a nonabelian Berrys phase that is
intimately related to the Aharonov-Bohm phase. (The Aharonov-Bohm phase depends
exclusively on the vector potential.) Even the strong nuclear interaction is
accurately described by a nonabelian gauge theory. Pure Maxwell theory is free
and so essentially trivial. It contains a noninteracting photon. In contrast,
pure Yang-Mills theory ![]() contains
self-interaction and is highly nontrivialFields listen to the Yang-Mills gauge
bosons according to the representation R that they belong to, and those that
belong to the trivial identity representation do not hear the call of the gauge
boson.
contains
self-interaction and is highly nontrivialFields listen to the Yang-Mills gauge
bosons according to the representation R that they belong to, and those that
belong to the trivial identity representation do not hear the call of the gauge
boson.
According to Froning and Roach, the representation R can be changed by surrounding a saucer-shaped spaceship with a toroidal EM field that distorts and perturbs the vacuum sufficiently to affect its permeability and permittivity. The vacuum field perturbations are simulated by fluid field perturbations that resulted in the same percentage change in disturbance propagation speed within the region of perturbation. The computational effort was simplified by solving only the Euler equations of fluid dynamics for wave drag. The resulting μo and εo perturbation solutions are shown in Figure 41.
In his discussion of the 1910 Einstein-Hopf model, Milonni describes their derivation of a retarding force or drag on a moving dipole as a result of its interaction with the vacuum zero-point field, which acts to decrease its kinetic energy. Assuming v << c, the retarding force due to motion through the ZPF thermal field is described with a fluid dynamics equation, F = R v, where v is the velocity of the dipole and R is a formula depending upon dipole mass and ZPF spectral energy density. Milonni also notes that due to recoil associated with photon emission and absorption, which are both in the same direction, the ZPF also acts to increase the kinetic energy of a dipole. Equilibrium is established when the increase in kinetic energy due to recoil balances the decrease in kinetic energy due to the drag.
It has been proposed by Rueda and Haisch, with a contract from NASA, that the ZPF can lose its Einstein-Hopf drag as the absolute temperature approaches zero, which would leave only the accelerating recoil force left. Furthermore, they propose that the ZPF can provide a directional acceleration to monopolar particles more effectively that to polarizable particles. They also suggest that if valid, the mechanism should eventually provide a means to transfer energy, back and forth, but most importantly forth, from the vacuum electromagnetic ZPF into a suitable experimental apparatus.
Quantum Coherence Accesses Single Heat Bath
One of the main criticisms of energy extraction from the ZPF is that it represents a single low-temperature bath and the second law of thermodynamics prohibits such an energy conversion. It is well-known that Carnot showed that every heat engine has the same maximum efficiency, determined only by the high-temperature energy source and the low-temperature entropy sink. Specifically, it follows that no work can be extracted from a single heat bath when the high and low temperature baths are the same.
However, a new kind of quantum heat engine (QHE) powered by a special quantum heat bath has been proposed by Scully et al. which allows the extraction of work from a single thermal reservoir. In this heat engine, radiation pressure drives the piston and is also called a Photo-Carnot engine. Thus, the radiation is the working fluid, which is heated by a beam of hot atoms. The atoms in the quantum heat bath are given a small bit of quantum coherence (phase adjustment) which becomes vanishingly small in the high-temperature limit that is essentially thermal. However, the phase associated with the atomic coherence, provides a new control parameter that can be varied to increase the temperature of the radiation field and to extract work from a single heat bath. The second law of thermodynamics is not violated, according to Scully et al., because the quantum Carnot engine takes more energy, with microwave input, to create the quantum coherence than is generated.
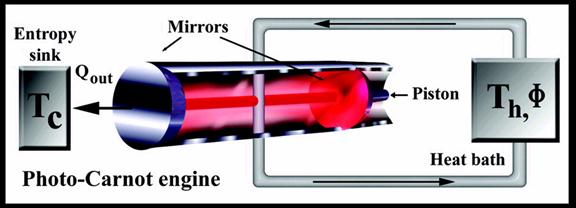
Figure 42 Photo-Carnot heat cycle diagram. Qin is
provided by hot atoms from bath.
The Photo-Carnot engine, shown in Figure 42, creates radiation pressure from a thermally excited single-mode field that can drive a piston. Atoms flow through the engine from the Th heat bath and keep the field at a constant temperature for the isothermal 1à 2 portion of the Carnot cycle (Figure 43). Upon exiting the engine, the bath atoms are cooler than when they entered and are reheated by interactions with the blackbody at Th and 'stored' in preparation for the next cycle.
The stimulus for the work came from two innovations in quantum optics: the micromaser and microlaser (Figure 32) and lasing without inversion (LWI). In micromasers and microlasers, the radiation cavity lifetime is so long that a modest beam of excited atoms can sustain laser oscillation. In LWI, the atoms have a nearly degenerate pair of levels making up the ground state. When the lower level pair is coherently prepared, a small excited state population can yield lasing (without inversion). In the QHE, the 'engine' is a microlaser cavity in which one mirror is a piston driven by the radiation pressure given by
P V = n h p c / L (40)
![]()
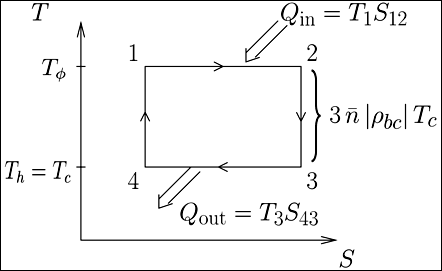 where P is the radiation pressure, V is the
cavity volume, n is the average number of thermal photons in the right mode (about
103), and L is the length of the cavity.
In Figure 43, an engine cycle diagram is shown which is a temperature versus
entropy graph for the Photo-Carnot engine, where |ρbc| ≈
3 x 10-6 is an off-diagonal density matrix element in the extension
of the quantum theory of a laser without inversion. Figure 43 contains a closed
cycle of two isothermal and two adiabatic processes (compare with Pintos
Figure 31). Qin is the energy absorbed during the isothermal
expansion and Qout is the energy given to the heat sink during the
isothermal compression. However, instead of two states which would render this
a classical engine, the QHE has three states, which can result in quantum
coherence. If there is a non-vanishing phase difference between the two lowest
atomic states, then the atoms are said to have quantum coherence. This can be
induced by a microwave field with a frequency that corresponds to the
transition between the two lowest atomic states. Quantum coherence changes the way the atoms interact with the cavity
radiation by changing the relative strengths of emission and absorption. In Figure 42, as the atoms leave the
blackbody at temperature Th they pass through a microwave cavity
that causes them to become coherent with phase Φ before they enter the
optical cavity. The temperature that characterizes the radiation is TΦ
which is
where P is the radiation pressure, V is the
cavity volume, n is the average number of thermal photons in the right mode (about
103), and L is the length of the cavity.
In Figure 43, an engine cycle diagram is shown which is a temperature versus
entropy graph for the Photo-Carnot engine, where |ρbc| ≈
3 x 10-6 is an off-diagonal density matrix element in the extension
of the quantum theory of a laser without inversion. Figure 43 contains a closed
cycle of two isothermal and two adiabatic processes (compare with Pintos
Figure 31). Qin is the energy absorbed during the isothermal
expansion and Qout is the energy given to the heat sink during the
isothermal compression. However, instead of two states which would render this
a classical engine, the QHE has three states, which can result in quantum
coherence. If there is a non-vanishing phase difference between the two lowest
atomic states, then the atoms are said to have quantum coherence. This can be
induced by a microwave field with a frequency that corresponds to the
transition between the two lowest atomic states. Quantum coherence changes the way the atoms interact with the cavity
radiation by changing the relative strengths of emission and absorption. In Figure 42, as the atoms leave the
blackbody at temperature Th they pass through a microwave cavity
that causes them to become coherent with phase Φ before they enter the
optical cavity. The temperature that characterizes the radiation is TΦ
which is
TΦ = Th (1 n ε cos Φ) (41)
where ε is the magnitude of quantum coherence, ε = 3|ρbc|. The second term in Equation (41) is also used in the QHE efficiency equation,
ηΦ = η ( Tc/Th ) n ε cos Φ (42)
Thus, depending on the value of Φ, the efficiency of the quantum Carnot engine can exceed that of the classical engine even when Tc = Th . It can therefore extract work from a single heat bath.
Inexplicably, Scully et al. fail to cite a previous work by Allahverdyan and Nieuwenhuizen that utilizes more rigorous physics for same purpose of extraction of work from a single thermal bath in the quantum regime with quantum coherence. The authors, perhaps, have more controversial statements in the article regarding free energy extraction. Using the quantum Langevin equation for quantum Brownian motion, they note that it has a Gibbs distribution only in the limit of weak damping, thus preventing the applicability of equilibrium thermodynamics. The reason is related to quantum entanglement and the necessary mixed state. Our main results are rather dramatic, apparently contradicting the second law: We show that the Clausius inequality dQ < TdS can be violated, and that it is even possible to extract work from the bath by cyclic variations of a parameter (perpetuum mobile). The physical cause for this appalling behavior will be traced back to quantum coherence in the presence of the near-equilibrium bath. It is also emphasized that the quantum coherence is reflected in the quantum noise correlation time which exceeds the damping time 1/ Γ.
Regarding the ZPF, it is interesting that the quantum Langevin equation is a consequence of the fluctuation-dissipation theorem of Equation (11). The authors note that part of the equation includes the fluctuating quantum noise, which has a maximum correlation time and therefore has a long memory (quantum coherence) at low temperature. The Brownian particle of interest also has semi-classical behavior due to its interaction with the bath, where there is a transfer of heat, even for T = 0.
The possibility of extracting energy from the bath is due to the nonequilibrium state, which is ensured by the switching energy ½ γ Γ<x2>o that is also a purely classical effect. The switching energy depends upon γ which is the damping constant and Γ which is the cutoff frequency. Both harmonic and anharmonic oscillation potentials are considered. The Brownian quantum particle strongly interacts with the quantum thermal bath, described by the Fokker-Planck equations.
Two formulations of the second law, namely, the Clausius inequality and the impossibility to extract work during cyclical variations, can be apparently violated at low temperatures. One could thus speak of a perpetuum mobile of the second kind. We should mention, however, that the number of cycles can be large, but not arbitrarily large. As a result, the total amount of extractable work is modest. In any case, the system energy can never be less than its ground state energyWe call them apparent violations, since, the standard requirements for a thermal bath not being fulfilled, thermodynamics just does not apply. Let us stress that also in the classical regime the harmonic oscillator bath is not in full equilibrium, but there noise and damping have the same time scale 1/ Γ, allowing the Gibbs distribution to save the day and thermodynamics to apply. Our results make it clear that the characterization of the heat bath should be given with care. If it thermalizes on the observation time, standard thermodynamics always applies. Otherwise, thermodynamics need not have a sayThe finding that work can be extracted from quantum baths may have a wide scope of applications such as cooling.'
In a physics commentary, Linke defends the second law by insisting that the work done by the Scully et al. piston (in Figure 42) is less than the work required to establish quantum coherence. Linke clarifies the Photo-Carnot process by stating, When the phase difference is adjusted to the value p, destructive interference reduces the likelihood of photon absorption, whereas emission from the upper level is not affected. This deviation from detailed balance between photon absorption and emission increases the photon temperature. The resulting temperature difference between photon gas and heat bath allows the photon Carnot engine to produce work in the absence of a hot bath.
Thermodynamic Brownian Motors
There is still another aspect of the ZPF that presents the possibility of energy extraction, which are nonequilibrium fluctuations a different representation of the single heat bath. Biasing the Brownian motion of a particle in an anisotropic medium without thermal gradients, the force of gravity, or a macroscopic electric field is a way that usable work is theoretically generated from nonequilibrium fluctuations, such as those generated externally or by a chemical reaction far from equilibrium. Fluctuation-driven transport is one mechanism by which chemical energy can directly drive the motion of particles and macromolecules and may find application in a wide variety of fields, including the design of molecular motors called Brownian motors and pumps.
Brownian motion, the random collisions with solvent molecules by a particle in a liquid, has been studied historically by Einstein as well as by Langevin. Langevins equation, as noted in the previous section, suggested that the forces on the particle due to the solvent can be split into two components: (1) a fluctuating force that changes direction and magnitude frequently compared to any other time scale of the system and averages to zero over time, and (2) a viscous drag force that always slows the motions induced by the fluctuation term. Related to the fluctuation-dissipation theorem of Equation (11), the amplitude of the fluctuating force is governed by the viscosity of the solution and by temperature, so the fluctuation is often termed thermal noise. Even in an anisotropic medium, the fluctuations are symmetric as required by the second law of thermodynamics, as are the dissipative drag force. Therefore, when all components of fluctuation-driven system are treated consistently, net motion is not achieved if it is an isothermal system, despite the anisotropy of a ratchet's teeth. However, a thermal gradient in synergy with Brownian motion can cause directed motion of a ratchet and can be used to do work but these are hard to maintain in microscopic and molecular systems. Recent work has focused, instead, on the possibility of an energy source other than a thermal gradient to power a microscopic motor.
Astumian
proposes a fluctuating electrical potential that causes the uphill transport of
a particle. A fluctuating potential energy profile is provided with
an anisotropic sawtooth function Usaw and periodically spaced
wells with no net macroscopic force. When the potential is off, the
energy profile is flat with a uniform force everywhere. When the potential is
turned on again, the particle is trapped in one of the wells. The result is
resolved into two components: the downhill drift and the diffusive
spreading of the probability distribution. For intermediate times,
it is more likely for a particle to be trapped in one of the
uphill wells if the potential were
turned back on, than between the first and second well. Thus,
turning the potential on and off cyclically can cause motion to the
right and 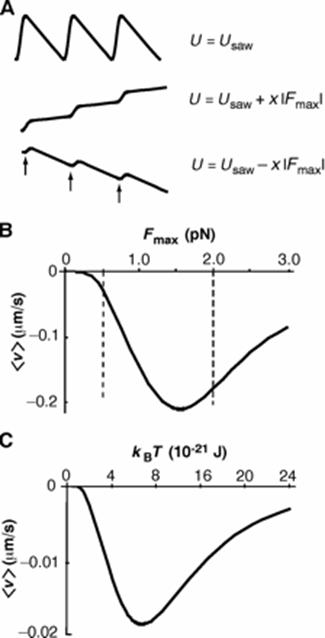 uphill against gravity despite the net force
to the left. The theory has been successfully tested with colloidal particles
with anisotropic electrodes turned on and off, as well as with an optical trap
modulated to create a sawtooth potential.
uphill against gravity despite the net force
to the left. The theory has been successfully tested with colloidal particles
with anisotropic electrodes turned on and off, as well as with an optical trap
modulated to create a sawtooth potential.
![]() Figure
44 shows the basic mechanism by which a fluctuating or oscillating force can cause
directed motion along a ratchet potential Usaw and also some
statistics of an example. The presence of thermal noise allows a subthreshold
fluctuating force to cause flow. The force is modulated between + Fmax where the average velocity <v> is
calculated as a function of Fmax where the dashed lines (B) indicate
the threshold forces. Another example is shown (C) where average velocity is
plotted as a function of the thermal noise strength kBT, where kB
is Boltzmanns constant and T is the absolute temperature and Fmax =
0.4 pN. The (C) graph shows that, up to a point, increasing the noise can
actually increase the flow induced by a fluctuating force. However, the (B) graph shows that for forces
near the optimum (about 1.5 pN in this example), the velocity decreases with
increasing noise.
Figure
44 shows the basic mechanism by which a fluctuating or oscillating force can cause
directed motion along a ratchet potential Usaw and also some
statistics of an example. The presence of thermal noise allows a subthreshold
fluctuating force to cause flow. The force is modulated between + Fmax where the average velocity <v> is
calculated as a function of Fmax where the dashed lines (B) indicate
the threshold forces. Another example is shown (C) where average velocity is
plotted as a function of the thermal noise strength kBT, where kB
is Boltzmanns constant and T is the absolute temperature and Fmax =
0.4 pN. The (C) graph shows that, up to a point, increasing the noise can
actually increase the flow induced by a fluctuating force. However, the (B) graph shows that for forces
near the optimum (about 1.5 pN in this example), the velocity decreases with
increasing noise.
A more general approach is suggested for analyzing fluctuation-driven transport using the diffusion equation with a probability density given by the Boltzmann distribution P(x) ≈ exp(-U/ kBT).
Since modulating the potential certainly requires work, Astumian believes there is no question of these devices being perpetual motion machines. The surprising aspect is that flow is induced without a macroscopic force. All of the forces involved are local and act on a length scale of the order of a single period of the potential. Yet the motion persists indefinitely, for many periods. However, the direction of the flow depends upon how the modulation is applied. Such devices are indicated to be consistent with the behavior of molecules.
In a dramatic confirmation of the Astumian theory, two subsequent experiments were performed by Linke et al. which applied an electron ratchet in a tunneling regime with a rocking-induced current (tunneling through and excitation over the ratchets energy barrier) flow in opposite directions. Thus the net current direction depends on the electron energy distribution at a given temperature. The practical aspect of this experimental approach is that a square wave source-drain voltage is applied with the time-averaged electric field being zero, similar to AC electricity, and yet the output net current is DC, similar to a rectifier.
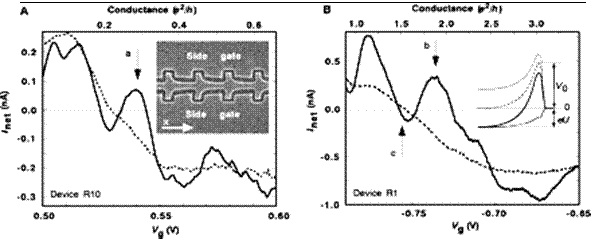
Figure 45A shows in the inset the asymmetrical darker regions which are etched trenches that laterally confine a two-dimensional sheet of electrons located parallel to the surface of a GaAs/AlGaAs heterostructure. Figure 45B inset compares the barrier height Vo with the electron energy |eU| < 1 meV. The trench's periodic variation in width induces a corresponding variation in electron confinement energy that creates asymmetric energy barriers at each constriction. When the square wave source-drain bias voltage is applied, the resulting current I is plotted for two devices R10 and R1. Because of the geometric asymmetry, the electric field along the channel produced by the voltage deforms the barriers in a way that depends on the polarity of the voltage, trapping the electrons in one of the side gates along the x direction. The quantum ratchet is thus established by confining electrons to an asymmetric conducting channel of a width comparable to the electron wavelength. The experiment demonstrates importance of resonant design and fulfills the theoretical prediction that a fluctuating voltage is sufficient to cause a unidirectional current.
![]()
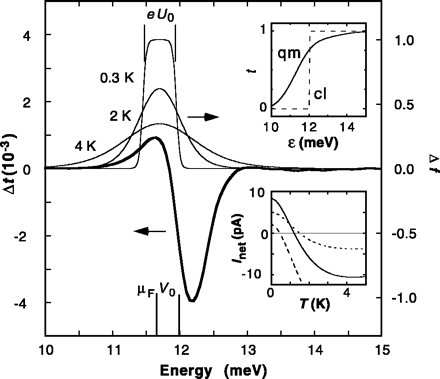 The detailed theoretical model of the
tunneling ratchet is shown in Figure 46. The difference ∆t between the
transmission functions for the barrier potential Vo in Figure 45B
inset is graphed (solid curve) for a rocking voltage Uo = 0.5 mV.
The bottom of Figure 46 shows visually
the approximate equality of the barrier height Vo and the Fermi
energy μF of 12 meV. The thin curves are identified by
temperature and are graphed against the energy range ∆f of the right hand
ordinate axis. The Figure 46 top inset shows the dramatic difference between
the solid curve quantum mechanical behavior (qm) and the classical (cl)
transmission function versus electron energy ε for Uo = 0. The
classical step function occurs at ε = Vo which is the Fermi energy μF.
Note the Figure 46 lower inset which summarizes the net current I in
picoamperes versus temperature, for rocking voltages Uo = 0.7 mV
(dashed curve), 0.5 mV (solid curve), and 0.3 mV (dotted curve). All
temperatures in this experiment were within a few degrees of absolute zero.
The detailed theoretical model of the
tunneling ratchet is shown in Figure 46. The difference ∆t between the
transmission functions for the barrier potential Vo in Figure 45B
inset is graphed (solid curve) for a rocking voltage Uo = 0.5 mV.
The bottom of Figure 46 shows visually
the approximate equality of the barrier height Vo and the Fermi
energy μF of 12 meV. The thin curves are identified by
temperature and are graphed against the energy range ∆f of the right hand
ordinate axis. The Figure 46 top inset shows the dramatic difference between
the solid curve quantum mechanical behavior (qm) and the classical (cl)
transmission function versus electron energy ε for Uo = 0. The
classical step function occurs at ε = Vo which is the Fermi energy μF.
Note the Figure 46 lower inset which summarizes the net current I in
picoamperes versus temperature, for rocking voltages Uo = 0.7 mV
(dashed curve), 0.5 mV (solid curve), and 0.3 mV (dotted curve). All
temperatures in this experiment were within a few degrees of absolute zero.
Transient Fluctuation Theorem
Another development in the thermodynamics of microscopic systems has recently redefined the concept of work. In a system connected to a single heat bath, uncertainties on the order of kBT will arise from the Boltzmann distribution of energies in the initial and final states, as well as from energy exchange with the heat bath as the system goes from initial to final energy states. Because of the thermal fluctuations or energy uncertainties, it has now been proven by theory and experiment, that the work cannot be uniquely specified, even if the path is known. When the system is microscopic, the fluctuations are significant and a transient fluctuation theorem has evolved to account for the behavior which takes the form,
P(W) / P(-W) = eW (43)
![]()
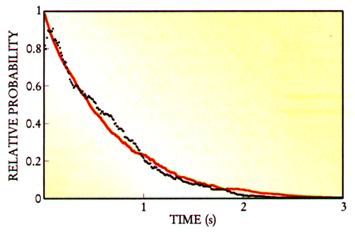 where W is the work divided by kBT
and P(W) is the probability of performing positive work over an interval of
time, while P(-W) is the probability of performing negative work over the same
period of time .
It needs to be clarified that in these microscopic systems, work is measured as
it is delivered to a vessel but half the time the system goes in reverse,
apparently violating the law of entropy. In Figure 47, a Poisson distribution
is shown of an optical trap interacting with an experimental vessel having
micron-sized beads. Though the trap exerted a restoring force, as for the
spring in Figure 2, the experimentally-determined values measured for the bead
position in the integrated fluctuation theorem showed a nonzero probability
for negative work, for up to two seconds.
where W is the work divided by kBT
and P(W) is the probability of performing positive work over an interval of
time, while P(-W) is the probability of performing negative work over the same
period of time .
It needs to be clarified that in these microscopic systems, work is measured as
it is delivered to a vessel but half the time the system goes in reverse,
apparently violating the law of entropy. In Figure 47, a Poisson distribution
is shown of an optical trap interacting with an experimental vessel having
micron-sized beads. Though the trap exerted a restoring force, as for the
spring in Figure 2, the experimentally-determined values measured for the bead
position in the integrated fluctuation theorem showed a nonzero probability
for negative work, for up to two seconds.
Imagine, as is often the case, that after a certain time, the bead has a higher energy than it had initially. Then, if the work done by the trap on the vessel (bead plus bath) is negative, energy has been delivered to both the bead and the optical trap interacting with the vessel. That energy came from the water bathjust the sort of energy transfer prohibited by the second law in the thermodynamic limit of infinitely large systems: Heat has been converted to work with 100% efficiency.
The generalized transient fluctuation theorem has various forms depending upon the application. For example, the probability ratio in Equation (43) can instead relate to entropy production w for forward and reverse time, where microscopic reversibility is an essential requirement. The theorem finds its greatest utility in the application to single heat baths and systems driven by a stochastic (random), microscopically-reversible (time-symmetric), periodic process. Then, the only Gaussian distribution that satisfies the fluctuation theorem has a variance that is twice the mean 2<w> = <(w-<w>)2>, which is a version of the standard fluctuation-dissipation relation of Equation (11). It is noted that entropy production, which is irreversible dissipation, is directly related to the fluctuations.
An example of a
systematic application of the fluctuation theorem, reminiscent of the quantum
ratchet concept seen previously, is a Metropolis Monte Carlo simulation by
Crooks, illustrated in Figure 48. A single particle occupies a finite number of
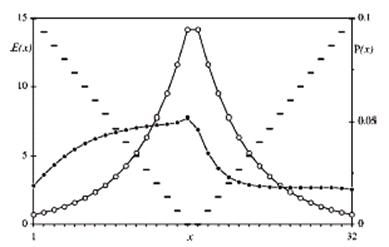 positions in a one-dimensional box with periodic
boundaries and coupled to a heat bath of T = 5. The energy surface E(x) is
outlined
positions in a one-dimensional box with periodic
boundaries and coupled to a heat bath of T = 5. The energy surface E(x) is
outlined ![]() by a series of dashed () lines. The
equilibrium distribution to be expected from such a potential well is shown as
a symmetric hill with open circles Ο since the particle is free to move
with equal probability to the right, left, or to stay put. However, every eight
time intervals, the energy surface moves to the right by one position.
by a series of dashed () lines. The
equilibrium distribution to be expected from such a potential well is shown as
a symmetric hill with open circles Ο since the particle is free to move
with equal probability to the right, left, or to stay put. However, every eight
time intervals, the energy surface moves to the right by one position.
In this way, the system is driven away from equilibrium and settles into a time-symmetric, nonequilibrium steady state distribution shown by black dots ●, skewed to the left. The master equation for this system can be solved exactly to compare with the theory.
Power Conversion of Thermal Fluctuations
![]()
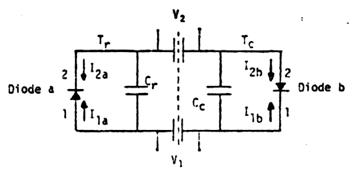 While
many recent scientific advances in the treatment of nonequilibrium energy
fluctuations have been reviewed so far, there are also developments in the area
of nonlinear equilibrium thermal fluctuations. Based on the Nyquist theorem
(another name for the fluctuation-dissipation theorem) and van Kampens work on
nonlinear thermal fluctuations in diodes, Yaters pioneering work involves the
use of microscopic diodes in a simple circuit, whose results gave higher
conversion efficiencies than the Carnot cycle for certain limiting cases as
these model sizes decreased.'
While the use of two heat baths suggests a thermionic energy source, his
detailed analysis makes it clear that the energy fluctuation conversion is
added to a heat pump thermal conversion cycle, for example, yielding a factor
of 10 improvement.
While
many recent scientific advances in the treatment of nonequilibrium energy
fluctuations have been reviewed so far, there are also developments in the area
of nonlinear equilibrium thermal fluctuations. Based on the Nyquist theorem
(another name for the fluctuation-dissipation theorem) and van Kampens work on
nonlinear thermal fluctuations in diodes, Yaters pioneering work involves the
use of microscopic diodes in a simple circuit, whose results gave higher
conversion efficiencies than the Carnot cycle for certain limiting cases as
these model sizes decreased.'
While the use of two heat baths suggests a thermionic energy source, his
detailed analysis makes it clear that the energy fluctuation conversion is
added to a heat pump thermal conversion cycle, for example, yielding a factor
of 10 improvement.
Yater offers a simplified master equation for the output rectified current from an independent particle model,
I (N) ≈ exp [ (β α)(N ½ ) (βm + αn)] 1 (44)
where β = q2 / kBTcC, N = the number of excess electrons in the total circuit capacitance C, and α = q2 / kBTrC. The designation of n and m are related: n = CcV/q and m = CrV/q where C = Cc + Cr. The forward and reverse diode currents in Figure 49 also combine in textbook fashion to produce the total current of Equation (44):
I (N) ≈ I1a I2b I2a I1b (45)
A Schottky barrier diode, for example, at the liquid Helium temperature of Tc = 1K can be used for the cold bath Tr in Figure 49. For such a diode the nonlinearity factor is β = 1.16 x 104 e/C where C is the capacitance of the diode (C ~ 10-16F) and e is the charge on the electron. A Schottky diode is also known to be formed between a semiconductor and a metal, with nonlinear rectifying characteristics and fast switching speeds.
Yater notes that for the long range design goals, sub-micron circuit sizes are required if all the high power goals of megawatts per square meter are to be achievedThe results of an analysis of the independent particle model for both classical and quantum effect, show that the reversible thermoelectric converter with power conversion of energy fluctuations has the potential of achieving the maximum efficiency of the Carnot cycle. The potential applications of this device can be seen to be universal. His patent #4,004,210 clarifies that the electric energy fluctuations are transmitted from the higher temperature diode to the lower temperature diode while the heat transfer is in reverse, which is unusual.
Upon reviewing the literature, Yater summarizes his findings: The relation of the second law of thermodynamics to the power conversion of fluctuation energy has been of recurring interest and study. The results of these studies have ranged from the conclusion that conversion of fluctuation energy is prohibited by the second law to the conclusion that the conversion of fluctuation energy is not limited by the second law of thermodynamics.
Rectifying Thermal Noise
Particles that move aperiodically due to thermal or external noise, in the presence of asymmetric periodic potentials, have also been called stochastic ratchets. These systems have the intriguing ability to rectify symmetric correlated noise and thus have the ability to produce a net electrical current. As a consequence of the fluctuation-dissipation theorem, the ratchet does not drift (as in the Metropolis Monte Carlo simulation of Figure 48) if it is in interaction only with a thermal bath. An external forcing must be used to produce the drift, according to the researchers, Ibarra-Bracamontes et al.
By describing the ratchet system in the Brownian particle regime with the Langevin equation (like Allahverdyan and Nieuwenhuizen), thermal noise is considered to have finite correlation times. This treatment yields a prediction of current production due to a time-dependent external force. In this case, the external force is either sinusoidal or stochastic. The generalized Langevin equation is an embellishment of Newtons equation, F = ma, describing a particle of mass m moving in an asymmetric periodic potential V(x) that forms the ratchet,
m d2x/dt2 = d(t) Γ(t t) dx(t)/dt dV(x)/dx + f(t) + Fext(t) . (46)
Γ(t) is the dissipation kernel, which in this case has memory and correlated with friction. The term, f(t), is the stochastic fluctuating thermal force exerted by the bath which has a usual stochastic property of being Gaussian with zero mean. By a numerical solution, Equation (49) does not show a net current in the absence of external forces (if Fext(t) = 0). However, adding a time-symmetric external force in general is a necessary and sufficient condition for the Langevin equation to yield a current flow in one direction.
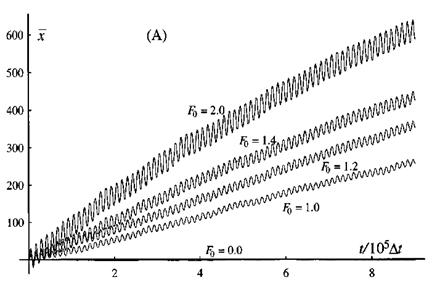
![]()
 Rather
than argue in favor of nonequilibrium fluctuations being present with a
symmetric correlated force, the emphasis is made in this case in favor of an external
origin for the force. In accordance with the second law of thermodynamics, the
assertion is also made here that 'one cannot extract a current from a
thermal bath, whether white or colored. Colored noise is where some frequencies
dominate the noise spectrum and is also referred to as pink noise. The average position of the electron <x>
is shown in Figure 50 for five different external force amplitudes versus time.
The solution demonstrates the Metropolis Monte Carlo simulation, with a
different ratchet design than Figure 48. However, it is not clear that
Ibarra-Bracamontes et al. have succeeded in proving their controversial claim
that any external forcing may be used to produce the drift but the
rectification of thermal noise due to an asymmetric external potential has been
demonstrated.
Rather
than argue in favor of nonequilibrium fluctuations being present with a
symmetric correlated force, the emphasis is made in this case in favor of an external
origin for the force. In accordance with the second law of thermodynamics, the
assertion is also made here that 'one cannot extract a current from a
thermal bath, whether white or colored. Colored noise is where some frequencies
dominate the noise spectrum and is also referred to as pink noise. The average position of the electron <x>
is shown in Figure 50 for five different external force amplitudes versus time.
The solution demonstrates the Metropolis Monte Carlo simulation, with a
different ratchet design than Figure 48. However, it is not clear that
Ibarra-Bracamontes et al. have succeeded in proving their controversial claim
that any external forcing may be used to produce the drift but the
rectification of thermal noise due to an asymmetric external potential has been
demonstrated.
An experimental demonstration of rectifying random thermal fluctuations involves ferrofluids, which are colloidal suspensions of nanoparticle ferromagnetic grains (~10 nm). In this case, the external potential is an anharmonic oscillating magnetic field created by Hemholtz coils Hy at a distance from the ferrofluid. It is regarded as a rotating magnetic field since there is a static magnetic field Hx at right angles to the oscillating field which sums to create rotation and angular momentum (Figure 51). The angular momentum of electromagnetic fields is a principle of classical physics. Without thermal fluctuations, relaxation dynamics tend to cause the particles to align with the field in the x-y plane and no average rotation nor torque is created. In the presence of thermal fluctuations however, stochastic transitions occur due to the magnetic field asymmetry, yielding slightly different probabilities for the magnetic orientational motion of the ferromagnetic grains, as discovered by Engel et al.
As
with the Photo-Carnot engine, the Fokker-Planck equation is also used in this
case for a quantitative solution of the induced torque effect in the
ferrofluid. Solving the equation by expansion in spherical harmonics, the
transitions between deterministic solutions become possible. The spatial
asymmetry and temporal anharmonicity of the potential results in slightly
different rates for noise-induced increments and decrements of [phase] φ,
respectively. As a result, a noise-driven rotation of the particles arises.
There is viscous coupling 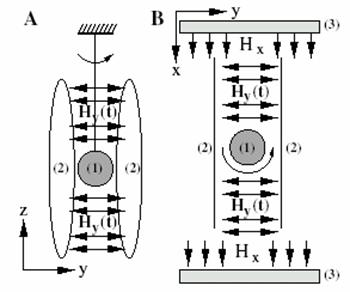 between the ferromagnetic grains and the
carrier liquid so that the individual torques add to create a macroscopic
torque per fluid volume, N = μo M x H. However, Engel et al.
admit that the time-averaged Nz is much smaller than the typical
values of the time-independent Nz calculated
between the ferromagnetic grains and the
carrier liquid so that the individual torques add to create a macroscopic
torque per fluid volume, N = μo M x H. However, Engel et al.
admit that the time-averaged Nz is much smaller than the typical
values of the time-independent Nz calculated  from the Fokker-Planck equation by adopting
the effective field method.
from the Fokker-Planck equation by adopting
the effective field method.
With an exploration of nonlinear perturbation techniques, Engel et al. admit that only a particularly chosen Langevin function yields the correct time-averaged z-component of the torque Nz, with static and dynamic magnetic field terms included. The expression for Nz shows that both the static magnetic field and the anharmonic part of the oscillatory component are essential for the directed rotation to occur.
Interestingly, the Brownian relaxation time is another parameter which had to be heuristically determined to achieve agreement between theory and experiment. It corresponded to a particle size of approximately 35 nm which is about three times the average particle size. Engel et al. conclude that the Brownian relaxation time must therefore correspond to the largest grains in the population rather than the average.
Engel et al. succeeded in rectifying rotational Brownian motion angular momentum. It is an experimental realization of the combined action of many individual nanoscale ratchets to yield a macroscopic thermal noise transport effect.
In regards to rectifying thermal electrical noise, it is worth mentioning the U.S. Patent #3,890,161 by Charles M. Brown that utilizes an array of nanometer-sized metal-metal diodes, capable of rectifying frequencies up to a terahertz (1012 Hz). Brown notes that thermal agitation electrical noise (Johnson noise) behaves like an external signal and can be sorted or preferentially conducted in one direction by a diode. The Johnson noise in the diode is also generated at the junction itself and therefore, requires no minimum signal to initiate the conduction in one direction. The thermal noise voltage is normally given by V2 = 4kBTRB where R is the device resistance and B is the bandwidth in Hertz. Browns diodes also require no external power to operate, in contrast to the Yater diode invention. Brown also indicates that heat is absorbed in the system, so that a cooling effect is noticed, because heat (thermal noise) energy energizes the carriers in the first place and some of it is converted into DC electricity. In contrast, the well-known Peltier effect is the closest electrothermal phenomenon similar to this but requires a significant current flow into a junction of dissimilar metals in order to create a cooling effect (or heating). Brown suggests that a million nickel-copper diodes formed in micropore membranes, with sufficient numbers in series and parallel, can generate 10 microwatts. The large scale yield is estimated to be several watts per square meter.
Quantum Brownian Nonthermal Recifiers

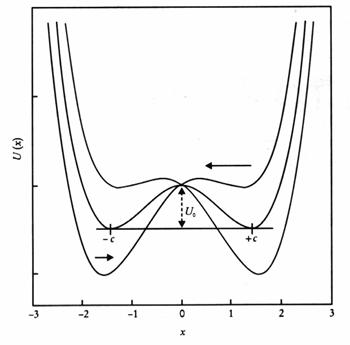 While
many researchers believe that the asymmetrical ratchet of one form or another
is essential in the conversion of stochastic fluctuations, there are others who
also find that stochastic resonance (SR) in threshold systems is a
sufficient substitute. The cooperation between the signal and noise
introduces coherence into the systemThis coherence is conveniently quantified
as the power spectral densityof the system responseThe earliest definition of
SR was the maximum of the output signal strength as a function of noise
An introduction to SR is shown in Figure 52 with a potential barrier Uo
separating two wells at +c. If the energy is subthreshold, the system
will be monotonic but adding an amount of noise on the order of Uo
allows the dichotomic system to oscillate. With a supra-threshold periodic
forcing, the two wells may have different net occupation levels (as arrows
indicate), with the output signal-to-noise ratio (SNR) following the input SNR
closely.
While
many researchers believe that the asymmetrical ratchet of one form or another
is essential in the conversion of stochastic fluctuations, there are others who
also find that stochastic resonance (SR) in threshold systems is a
sufficient substitute. The cooperation between the signal and noise
introduces coherence into the systemThis coherence is conveniently quantified
as the power spectral densityof the system responseThe earliest definition of
SR was the maximum of the output signal strength as a function of noise
An introduction to SR is shown in Figure 52 with a potential barrier Uo
separating two wells at +c. If the energy is subthreshold, the system
will be monotonic but adding an amount of noise on the order of Uo
allows the dichotomic system to oscillate. With a supra-threshold periodic
forcing, the two wells may have different net occupation levels (as arrows
indicate), with the output signal-to-noise ratio (SNR) following the input SNR
closely.
Anomalous transport properties, using SR, which do not exploit the ratchet mechanism have been investigated in driven periodic tight-binding (TB) lattices near zero DC bias with the combined effects of DC and AC fields, or DC field and external noise. In particular, Goychuk et al. have found that periodic TB lattices can be driven by unbiased nonthermal noise generated from the vacuum ZPF, generating an electrical current as a result of a ratchetlike mechanism, as long as there is quantum dissipation in the system.
Theoretically introducing quantum dissipation with an ensemble multi-state model of harmonic oscillators coupled to the driven system, along with an unbaised, time-dependent random force (characterized by an external, time-dependent random electric field, η(t) = eaEη(t)/h), yields the noise-averaged stationary quantum DC electrical current Jst = e(lim tà∞)d<q(t)>/dt and quantum diffusion coefficient D. The nonthermal fluctuations are given discrete, quantum values with probabilities as QED dictates. It is assumed that neither the temperature nor the nonthermal fluctuations can cause any essential occupation of higher energy levels for the dissipation model.
Goychuk et al. succeed in demonstrating that without dissipation, for any field, the stationary DC current is always zero. An initially localized particle, as in a crystal, does not produce a current in the absence of dissipation. However, considering the effect of adding unbiased fluctuations η(t) on Bloch oscillations, Goychuk develops a master equation which includes a real-time quantum Monte Carlo calculation yielding a good approximation for a TB particle at environmental temperatures and/or strong dissipation when transport includes sequential tunneling. Bloch functions describe an electron in a periodic lattice with a sinusoidal wave function conditioned by a lattice periodicity function. Driven tunneling dynamics in Bloch oscillation system is the subject of another paper Goychuk has coauthored with efficient determination of the optimal control of quantum coherence.
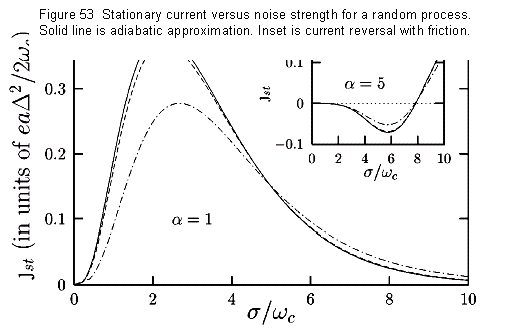
In Figure 53, the production of rectified electrical current Jst is
shown with an ohmic friction factor α = 1 graphed against changes in
fluctuation noise strength σ for a dichotomic (two-choiced) random process
with zero mean and asymmetry parameter of ξ = ½. While the solid
line is adiabatic, the dashed lines depict non-adiabatic autocorrelation times
of 0.1ωc and ωc respectively from top down,
where ωc is the cutoff frequency. The inset graph is an
interesting current reversal that occurs under a case of strong friction α
= 5 which is related to SR. Because the current appears as the nonlinear
response to the aperiodic external signal, the existence of this maximum [in
Figure 53] can be interpreted as a signature of aperiodic quantum stochastic
resonance.

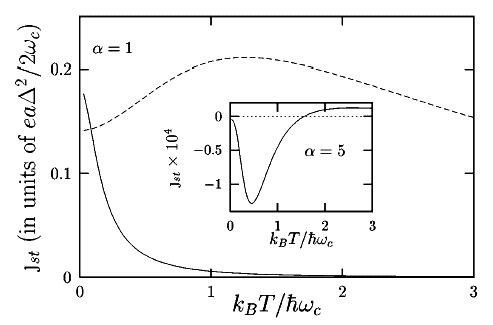
The stationary current is also found to depend on temperature, which is the signature of aperiodic quantum stochastic resonance (AQSR). In Figure 54, the rectified current is shown versus temperature for a fluctuation noise strength σ =0.5ωc (solid line) and σ = 7ωc (dashed line) while friction α = 1 and asymmetry ξ = 1.
In the presence of unbiased, asymmetric forcing, a noise-directed current always occurs in a dissipative TB lattice, because of the ratchet-like effect of the asymmetric forcing, like the stochastic ratchets that rectify thermal noise. With stochastic resonance, nonthermal fluctuations are effectively rectified, creating a measurable current. Goychuk believes that the effect should be already observable in superlattices and/or optical lattices.
For reference, it is worth mentioning that with crystal lattices, thermal fluctuations appear at environmental temperatures, with ½ mωo2<u2> = 3(½kBT) energy level where m and ωo are the mass and frequency of the harmonic oscillations and u is the displacement from a fixed lattice site. The nonthermal oscillations associated with ZPE are mωo2<u2> = 3(½hωo) in terms of energy, adding to the lattice thermal fluctuations.
Vacuum Field Amplification
With the introduction to AQSR along with the rectification of nonthermal noise, it makes sense to investigate the amplification of quantum noise. Milonni points out that the vacuum field may be amplifiedif the spontaneously emitted radiation inside the cavity is amplified by the gain medium, then so to must the vacuum field entering the cavity. Another way to say this is that quantum noise may be amplified. Since the SR TB lattice current output depends on the noise level, as in the Goychuk simulation, the optimum level of energy extraction depends on parameter control, as in quantum optics, which utilizes quantum noise amplification. This is similar to ASE which also uses a gain medium.
The actual content of quantum noise and vacuum polarization may still remain a mystery after all of the Chapter 4 analysis. Milonni notes that even though heavier virtual particle pairs like muons, pions, etc. may take part in virtual polarization, the majority of the manifested particles will always be electron-positron pairs because of the 1/m2 mass dependence of the nonexchange term between the two current densities for the electron and the negative-energy states of the ZPF. Jackson notes that the Weisacker-Williams method of virtual quanta treats every scattering impact or close encounter between charged particles as a Fourier collection of virtual particles which are equal to the electric field pulse radiated to the target. This method, in consonance with QED, gives the frequency spectrum, cutoff, and number of virtual particles per unit energy interval.
Summary
This study was predicated on the existing volume of data already in the scientific literature regarding the nonthermal vacuum fluctuations that comprise ZPE. The assessment of the feasibility of zero-point energy extraction by humans from the quantum vacuum for the performance of useful work in the electrical, fluidic, thermodynamic, and mechanical conversion modalities is determined in this chapter.
Analyzing the specific experiments, theories, simulations, measurements and predictions in this study offers a wealth of details concerning the energetic operation of ZPE throughout the universe. As a result, it can possibly be argued from an historical perspective that, because nature already extracts ZPE for the performance of useful work, humans eventually will be able to so as well. Acknowledging the need for robust, concentrated energy sources in the world, any study of the concept of energy extraction and production should address the corresponding utility and energy quality. Therefore, this summary addresses the electrical power output and the practicality of the conversion mode and method.
This study finds that at the present time, the categories of the present major inventive ZPE conversion modes includes 1) electromagnetic conversion, 2) Casimir cavity mechanical engine, 3) fluid dynamics techniques, and 4) quantum thermodynamic rectifiers. Under these major headings are individual methods such as 1a) focusing vacuum fluctuations, 2a) cavity QED, 2b) spatial squeezing, 2c) Casimir cavity geometry design, 2d) Casimir stress enhancement, and 2e) vibrating cavity photon emission, 3a) inertial effects, 3b) hydrodynamic model, 3c) Casimir cavity, 4a) quantum coherence, 4b) Brownian motors, 4c) transient fluctuations, 4d) thermal fluctuation rectifiers, and 4e) nonthermal Brownian rectifiers, as shown in Table 1 with relevant author names.
Table 1 - ZPE Conversion Modes & Methods
|
Electromagnetic |
Mechanical |
Fluid Dynamic |
Thermodynamic |
|
Dual sphere - Mead |
Casimir engine - Pinto |
Inertia Effects - Froning |
Quantum coherence - Allahverdyan, Scully |
|
Focusing ZPE - Ford |
Cavity QED - Haroche |
Hydrodynamic model Bohm |
Brownian motors - Astumian |
|
Spatial squeezing- Hu |
Casimir cavity - Maclay |
Transient fluctuation theorem - Crooks |
|
|
Casimir cavity optimized design - Maclay |
Thermal fluctuation rectifiers Brown, Ibarra-Bracamontes, Engel |
||
|
Vibrating cavity photon emission - Hizhnyakov |
Quantum Brownian nonthermal rectifiers - Goychuk |
Electromagnetic Conversion
In the electromagnetic energy conversion process, the proposed Mead configuration of two spheres in close proximity was analyzed for four different size categories, each of which are a thousand times smaller than the previous one. The microsphere category seemed to match the Mead design closely but was found to be lacking in sufficient scattering intensity, even when substituting conducting spheres which have the highest scattering cross section. The decrease of dielectric constant with frequency also was a problem for most materials. The ZPF energy density and resonant photon energy for the microsphere were only moderate and are summarized in Table 2, along with the other three spheres.
The nanosphere, as shown in Figures 16 and 17, demonstrates the present state of the art in nanotechnology assembly. The spectral energy density of Equation (16) for the nanosphere increases by a billion times over the microsphere even though the sphere size is reduced by a billion times. Upon integrating over a decade of frequencies with Equation (21) (see Table 2), a thousand times increase in ZPE density is calculated with each successively smaller sphere. However, no significant vacuum polarization is available for nano-sized particles, which is an energetic, physical manifestation of ZPE.
The picosphere is interesting in that Meads beat frequency concept can theoretically be realized with pairs of atoms very close in atomic weight such as platinum and gold or hydrogen and deuterium. However, the engineering challenges of such an assembly would be prohibitive, even if one could foresee a significant overunity energy production per pair. Furthermore, even with the advanced techniques such as Fords focusing of vacuum fluctuations, textbook upscattering or resonant fluorescence, etc., paired atoms of choice still have a technological barrier, lacking compatibility with any existing amplification or conversion transducer, such as those seen in Figure 21.
With the femtosphere, QED principles inherent to ZPE, start to emerge. In one sense, the femtosphere has become almost too small to manage individual particles, if they are in contact. In another sense, the size presents other opportunities such as with the ion trap, where electron femtospheres can be collected, for example. However, even as the advantage of working with electrons as ZPE receivers becomes more apparent, it is obvious much more research is needed.
Overall, the Mead patented method for utilizing ZPE collectors and resonators certainly presents a design or a collector that amplifies scattering, though Mead only analyzes a single sphere. The ZPF energy density of Equation (21) is the most relevant, showing the quartic increase of energy with frequency even though there is a cubic decrease of volume with each successive sphere. In the final assessment, given the extent of the experimentation that is required for success with this concept for extraction of useful energy, all four spheres of interest still do not receive a feasibility rating of overall confidence that would qualify it for endorsement from scientists, engineers, or investors. Using the realistic power production level or anticipated work output as a measure of energy quality, this invention receives a poor energy quality rating.
Table 2 presents more energy data for each sphere, with photon energy for the corresponding wavelength and the Einstein energy content added for comparison. The main observation with this tabular summary is that the ZPE energy for a given spherical volume finally equals (same order of magnitude) the Einstein energy content of matter as well as the photon energy of the corresponding wavelength. While the scattering cross section may seem to offer some advantages at larger sphere diameters, the equal weighting of light, matter, and vacuum for a femtosphere has to be extraordinarily inviting for the vacuum engineer and an area worthy of further research.
Table 2 - Energy and Cross Section of the Spheres
|
Microsphere |
Nanosphere |
Picosphere |
Femtosphere |
|
|
Photon energy |
1 eV |
1keV |
1 MeV |
1 GeV |
|
E = mc2 |
Si: 1044 eV |
Ag: 1017 eV |
Pt: 1011 eV |
p: 940 MeV |
|
ZPE energy |
390 meV/μm3 |
390 eV/nm3 |
390 keV/pm3 |
390 MeV/fm3 |
|
Physical cross sectional area |
3 x 10-12 m2 |
3 x 10-18 m2 |
3 x 10-24 m2 |
3 x 10-30 m2 |
|
Scattering cross section |
10-8 m2 |
10-15 m2 |
10-21 m2 |
10-30 m2 |
Mechanical Casimir Force Conversion
The Casimir force presents a fascinating exhibition of the power of the ZPF offering about one atmosphere of pressure when plates are less than one micron apart. As is the case with magnetism today, it has not been immediately obvious, until recently, how a directed Casimir force might be cyclically controlled to do work. The optically-controlled vacuum energy transducer however, proposed by Pinto, presents a powerful theoretical case for rapidly changing the Casimir force by a quantum surface effect, excited by photons, to complete an engine cycle and transfer a few electrons. The exciting part of Pintos invention is the QED rigor that he brings to the analysis, offering a convincing argument for free energy production. The nano-fabrication task that is presented, however, is overwhelming. Besides mounting nanolasers inside the Casimir cavity, the process suggests that a 10 Khz repetition rate is possible with a moving cantilever, without addressing the expected lifespan. The energy production rate is predicted to be robust (0.5 nW per cell or 1 kW/m2), which could motivate a dedicated research and development project in the future. However, the Casimir engine project of Pintos appears to be a long-term, multi-million dollar investment at best.
Utilizing some of the latest cavity QED techniques, such as mirrors, resonant frequencies of the cavity vs. the gas molecules, quantum coherence, vibrating cavity photon emission, rapid change of refractive index, spatial squeezing, cantilever deflection enhancement by stress, and optimized Casimir cavity geometry design, the Pinto invention may be improved substantially. The process of laser irradiation of the cavity for example, needs to be replaced with one of the above-mentioned quantum techniques for achieving the same variable Casimir force effect, with less hardware involved. At the present stage of theoretical development, the Pinto device receives only a moderate rating of feasibility. Its energy quality rating, however, is very high.
Fluid Dynamics
In the fluid dynamics analysis of the vacuum presented by Froning, it was convincingly argued that the permittivity and permeability of the vacuum can be reduced effectively by nonabelian electromagnetic fields, specifically by utilizing alternating current toroids at resonant frequencies.
While this research does not directly produce electricity, the energy extraction indirectly achieved by the use of the Froning prototype is in the form of energy conservation. By reducing the drag and inertia normally experienced by a spaceship in space, it will save a significant amount of energy, which is equivalent to generating it. The referenced information from Rueda and Haisch as well as from Maclay supports the validity of Fronings fluid dynamic approach. At its present stage of development, the feasibility rating is low, with an energy quality rating of high.
Thermodynamic Conversion
The Photo-Carnot engine is an interesting theoretcial device that relies upon quantum coherence to yield a cyclical radiation pressure for the piston-driven engine. The phase induced with the quantum coherence, provides a new control parameter that can be varied to increase the temperature of the radiation field and to extract work from a single heat bath. The claim is made that the second law of thermodynamics is not violated, according to Scully et al., because the quantum Carnot engine takes more energy, with microwave input, to create the quantum coherence than is generated. However, it is possible that as efficiency improvements are made, the output will exceed the input as is the trend with the other thermodynamic engines analyzed in this study. After all, depending on the value of the phase Φ, the efficiency of the quantum Carnot engine can already exceed that of the classical engine even when Tc = Th. The capability of extracting heat from a single reservoir should be regarded as a requirement for a ZPE thermodynamic transducer. With the added endorsement of Allahverdyan and Nieuwenhuizen, the Photo-Carnot engine is rasied to a perpetuum mobile of the second kind. The number of cycles cannot be arbitrarily large apparently, and the total amount of extractable work is modest. However, the standard requirements for a thermal bath are not fulfilled, according to Allahverdyan and Nieuwenhuizen, so thermodynamics just does not apply. For these reasons, the Photo-Carnot invention has great potential for becoming a ZPE energy producer and receives a high feasibility rating, with moderate energy quality rating.
The Brownian motors proposed by Astumian (Figures 44) utilize Langevins equation, also mentioned in connection with the quantum coherence of Scully et al. Astumian emphasizes the fluctuating energy source (thermal noise) and the dissipation (viscous drag) that is essential to the fluctuation-dissipation theorem, fundamentally important to the ZPF. With Astumians Brownian motors, the oscillating potential also needs an asymmetrical ratchet to ensure one-way transport. The ratchet concept, while very feasible and proven by two experiments, offers only a limited production of current with underunity efficiency. Astumian notes that with the viscous drag of the solvent, all of the energy gained by the ratchet steps is dissipated with an overall thermodynamic efficiency of less than 5%.
The tunneling electron ratchet experiment performed by Linke et al., seen in Figures 45-46, is an encouraging demonstration of the Brownian motor. Linke generates a maximum of 0.2 nA with about a millivolt of source-drain rocking voltage, at the picowatt or picojoule level, which is encouraging. However, with only between 1% and 5% rectification of the total current, the efficiency is also quite as low as Astumian.
With the analysis of the transient fluctuation theorem, it becomes apparent that with microscopic systems, the performance of negative work has a high probability, apparently violating the law of entropy. The Metropolis Monte Carlo simulation of Crooks in Figure 48 is similar to the quantum ratchet concept however, and doesnt offer an advantage over the other techniques.
The Yater method for power conversion of energy fluctuations is in the same category as rectifying thermal noise. While the Yater invention has an impressive assembly of patents and journal articles, the process requires two heat sources separated by a large spread in temperature. This makes the overall analysis of the device difficult to analyze except by conventional means with underunity energy output projections. His claims for a 10 times improvement over heat pumps is intriguing and the detailed plans in his patent encourage further research, with a reasonable feasibility projected and high energy quality.
The work by Ibarra-Bracamontes et al. is another confirmation of rectifying thermal fluctuation noise. It is interesting for theoretical analysis but the type of signals that are possible for external forcing is not made clear. Rectifying random thermal fluctuations with ferrofluids adds a new twist that is unique, especially when rotational energy is not available directly from the ZPF. Engel et al. offer a fascinating experiment for consideration, consistent with the rectification of thermal fluctuations for linear motion. However, the driving potential is a complex oscillating magnetic field with a field intensity as high as the static field which is also required (several kA/m). Both are generated by a commercial electromagnet. The work output that should be calculated in time-averaged torque multiplied by rotational distance will predictably be only a few percent of the input, at best. It is a good demonstration but does not seem to represent a practical concept for motoring or rotational work. Therefore, it receives a high feasibility rating but low energy quality.
The Brown patent rectifying thermal electrical noise with nano-sized metal-metal diodes is probably the most exciting invention analyzed in Chapter 4. Though the inventor does not acknowledge a ZPE contribution to Johnson noise, it is reasonable to project that the Brown diode arrays will rectify nonthermal fluctuations as well as thermal noise. With no external input needed for conduction, nor a minimum voltage to overcome the usual diode barrier, the potential for free energy production seems quite high. The attractiveness and projected consumer interest for such a solid state, zero-maintenance device is also very high. Not only is the fabrication understandable and straightforward but the description of a cooling effect (negative kinetic energy) from the conversion of thermal noise (positive kinetic energy) is also scientifically and thermodynamically acceptable. The energy density of several watts per square meter is reasonable and robust. However, this quantity should be calculated in watts per cubic meter, since the filled Millipore sheets can easily be stacked vertically as well. Another important calculated parameter for space power is the amount of watts per kilogram, which is probably moderate to high in this case. It is possible with modern nanotechnology that this invention could compete with the battery market. Not only is the feasibility given the highest rating for this invention, but the energy quality rating is also given the highest rating as well.
Stochastic resonance is an emerging energy field that now is being used to substitute for ratcheting in the Brownian rectifiers. The work by Goychuk demonstrates the aperiodic quantum stochastic resonance (AQSR) that is essential for these rectifiers to work in a solid state environment of a tight-binding crystal lattice. With near zero DC bias, the invention is very attractive for many reasons. The ratchetlike mechanism of Goychuk is a valuable substitute for the Astumian style of Brownian motor requiring physically fabricated ratchets. It does not require a static bias, which is a distinct improvement over previously analyzed Brownian motor requirements. The stationary current is also found to be nonzero for unbiased noise, demonstrating a DC rectification, as long as there is some degree of asymmetry in the noise. As a result, the invention combines the noise and the asymmetric driving force into one signal, which is also an advantage over lesser ZPE models. The AQSR design has the ability to rectify asymmetric, unbiased, nonthermal noise, including quantum fluctuations as well, producing a measurable electrical current in a solid state crystal lattice. The only remaining variables are the amount of quantum dissipation required for the effect, the optimum operating temperature, the anticipated energy efficiency and the projected difficulty inherent in creating asymmetry with nonthermal noise that naturally tends to be symmetric in time and space. These variables may be of a sufficiently minor concern for the Goychuk invention to actually offer a gateway to the future of ZPE electricity generation. Many parts of the invention fit the ideal impedance matching of energy source behavior with energy transducer behavior. For example, quantum fluctuations are shown by Goychuk to simply require quantum dissipation and a slight asymmetry, which is less energy intensive overall than creating a quantum coherence. This invention is given the highest rating for feasibility and the highest rating for energy quality.
Conclusions
The risk analysis that is often integrated into a feasibility study that is dedicated to a single development plan is really a process to assign a degree of likelihood to stages of a project. The feasibility rating standard adopted in Chapter 5 is equivalent to such an analysis.
The results of this study finds varying feasibility ratings and energy quality ratings for the four modes of energy conversion from the ZPF. For the Electromagnetic modality, in the present stage of development, the overall method is rated unfeasible with poor energy quality, given the limitations of todays technology capabilities. The Mechanical modality fares better with a moderate feasibility rating, at the overall present stage of development, with a very high energy quality rating. The Fluid Dynamic modality drops back with a low feasibility rating but high energy quality rating. The Thermodynamic modality shines with the highest feasibility rating and the highest energy quality rating.
The overall conclusions drawn from this study support the introductory physical description of the quantum vacuum. Furthermore, the hypothesis of a ZPF vibrating with measurable mechanical pressure, electromagnetic activity, and nonthermal energy is also supported by the scientific evidence uncovered by this study. The fluid dynamics information about ZPE was a reassuring fulfillment of the fourfold modality expectation. There is also a consistency with previous research going back to the early days of QED, which adds a reliability and confidence level to the normally unsettling nature of ZPE. Further research is needed however, as outlined briefly in the next section, to fully exploit the discoveries of energy extraction from the quantum vacuum.
The implications of this study to the emerging field of discipline called vacuum engineering are enormous and far-reaching: An up-to-date assessment of the state of the art has been accomplished by this comprehensive study. Based on this engineering physics achievement, with the feasibility and energy quality ratings therein, it can be reasonably expected that at least one business plan will be generated for a ZPE invention, perhaps for the first time in history. Such a development offers the business world an opportunity to benefit from the most plentiful energy source that also now has been found to have a certain level of practicality and moderate risk assessment, compatible with competing enterprises. As a result of this study, an opportunity has emerged for the public to benefit from some of the ZPE unusual ubiquitous qualities, such as making many completed ZPE transducers completely portable and possibly installing lifetime ZPE transducers in every appliance. The implications of this study are that future generations may finally relinquish fossil fuels in favor of ZPE.
Recommendations
Based on the quality of research uncovered and the level of agreement between theory and experiment demonstrated, specifically by the thermodynamic mode of ZPE conversion, it is recommended that further attention and funding be primarily dedicated to the exploitation of zero-point energy extraction, beginning with the microscopic realm. While the other three modalities offer interesting and promising developments, the feasibility rating and energy quality rating is the highest with the thermodynamic mode. In particular, it is recommended that 1) metal-metal nanodiodes should be researched, with attention to the Johnson noise voltage and purported lack of diode barrier, along with the possible mass production of high density substrates; 2) more ratchet and ratchetlike asymmetries should be researched, by government, industry and academia, so that a TB lattice or diode assembly may one day offer a truly solid state transducer for ZPE; 3) research should continue into quantum coherence, refractive index change, and stochastic resonance with a goal of reducing the present relatively large energy investment, so that more robust avenues of product development in ZPE thermodynamics may be achieved. Brownian motors, thermal fluctuation rectifiers, and quantum Brownian nonthermal rectifiers utilizing AQSR have already achieved a level of theoretical and experimental confidence where further physics research and engineering studies can offer fruitful rewards in the production of rectified DC electricity. This mode of ZPE conversion research and development needs to be continued with earnest in order to expand mankinds woefully limited portfolio of energy choices.
A broad outline of how to undertake the recommended development work would include specific tasks and milestones associated with a) the confirmation of ZPE quantum effects described in this study on a larger scale; b) replication of results but also optimization of results; and c) engineering tasks of conductor and semiconductor design, nanowires and ohmic contacts. All of these, along with other tasks not mentioned, need to be included. The project would also include estimates of output current and energy production with any given geometry. Parallel development paths in research and development will always accelerate the completion of the optimum design. A market study should also accompany the work, so a clear focus on the existing niche to be filled is maintained. A national or international project proposal that estimates the required project scope, resources, break-even point and identifies major milestones, has to be formulated, if major progress in ZPE usage is to be achieved. Simply commissioning another study to follow up this study will lead only to institutionalizing the effort without accomplishment of set goals.
This feasibility study of ZPE extraction for useful work has presented a balanced and detailed assessment with scientific integrity, engineering utility and the likelihood of success for further development. It can be concluded that zero-point energy is deserving of more attention by engineers and entrepreneurs as a serious and practical energy source for the near future. The proposed project plan for ZPE development, yet to be written, has been reduced to a business endeavor and an exercise in return on investment.
NASA website: www.grc.nasa.gov
Zinkernagel, Henrik. High Energy Particles and Reality. Ph.D. Thesis, University of Copenhagen, 1999, p. 25
Petersen, I. Peeking inside an electrons screen. Science News. Vol. 151, Feb. 8, 1997, p. 89
Deffeyes, Kenneth. Hubberts Peak: The Impending World Oil Shortage. Princeton University Press, Princeton, 2001, p. 5
Isaev, P. S. Quantum Electrodynamics at High Energies. American Institute of Physics, NY, 1989, p.33
Yam, Philip. Exploiting Zero-Point Energy. Scientific American. December, 1997, p. 84
Browne, Malcolm. Physicists confirm power of nothing, measuring force of quantum foam. The New York Times. January 21, 1997, p. C2
Forward, Robert. Extracting electrical energy from the vacuum by cohesion of charged foliated conductors. Phys. Rev. B. 30, 4, 1984, p.1700
Mead, Frank. System for Converting Electromagnetic Radiation Energy to Electrical Energy U.S. Patent #5,590,031, Dec. 31, 1996, Figure 1
Fink, Donald. Electrical Engineers Handbook, McGraw-Hill, New York, 1975, p.10-39
Mead, Frank., Figure 5
Cox, Larry T. Calculation of Resonant Values of Electromagnetic Energy Incident Upon Dielectric Spheres Phillips Laboratory, Air Force Material Command, PL-TR-93-3002, February, 1994, p. 17
Seto, William W. Schaums Outline Series: Theory and Problems of Mechanical Vibrations. Schaum Pub. Co., New York, 1964, p.22
Mead, Frank., Figure 6
Fink, Donald., p. 6-36
Morse, Philip M. and Herman Feshbach. Methods of Theoretical Physics, Part II, McGraw-Hill, New York, 1953, p.1485
Ibid., p. 1485
Jackson, J.D. Classical Electrodynamics. J. Wiley, New York, Second Edition, 1975, p. 452
Sun, Yugang, et al. Shape-Controlled Synthesis of Gold and Silver Nanoparticles Science, Vol. 298, No. 5601, p. 2176
Snow, T. P. and J. M. Shull. Physics, West Pub. Co., St. Paul, 1986, p. 744
Fink, p. 10-42
Electromagnetic Spectrum TRW, Inc., Electronics Systems Group, Redondo Beach, CA, October, 1986
Tipler, Paul A. Foundations of Modern Physics. Worth Publishers, NY, 1969, p. 195
Duderstadt, James and L.. Hamilton, Nuclear Reactor Analysis, J. Wiley & Sons, New York, 1976, p. 54
Ibid., p. 49
Jackson, p. 803
Baym, Gordon. Lectures on Quantum Mechanics. Benjamin/Cummings, Reading, 1978, p. 211
Brink, G. O., Nonresonant Ion Trap Review of Scientific Instruments, Vol. 46, No. 6, June, 1975, p. 739
Ibid., p. 740
Pinto, F. Engine cycle of an optically controlled vacuum energy transducer Phys, Rev. B, Vol. 60, No. 21, 1999, p. 14745
Ibid., p. 14746
Gourley, P. Nanolasers Scientific American, March, 1998, p. 57
Dodonov, V.V. Squeezing and photon distribution in a vibrating cavity J. Phys. A: Math Gen. V. 32, 1999, p. 6720
Ford, L.H. et al. Focusing Vacuum Fluctuations Casimir Forces Workshop: Recent Developments in Experiment and Theory, Harvard University, November 14-16, 2002, p. 19
Zheng, M-S., et al. Influence of combination of Casimir force and residual stress on the behaviour of micro- and nano-electromechanical systems Chinese Physics Letters, V. 19, No. 6, 2002, p. 832
Maclay, J. Unusual properties of conductive rectangular cavities in the zero point electromagnetic field: resolving Forwards Casimir energy extraction cycle paradox Proceedings of Space Technology and Applications International Forum (STAIF), Albuquerque, NM, January, 1999, Figure 1, p. 3
Ibid., Figure 2, p. 4
Sagan, Carl. Cosmos, Random House, New York, 1980, p. 37
Froning, H.D. and R.L. Roach Preliminary simulations of vehicle interactions with the quantum vacuum by fluid dynamic approximations Proceedings of 38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, July, 2002, AIAA-2002-3925, p. 52236
Ibid., p. 52237
Ibid., p. 52239
Scully, M.O. et al. Extracting work from a single heat bath via vanishing quantum coherence Science, Vol. 299, Issue 5608, 2003, Figure 1, p. 862
Ibid., Figure 2, p. 865
Astumian, R. D. Thermodynamics and Kinetics of a Brownian Motor Science, Vol. 276, Issue 5314, Figure 3, p. 919
Linke, H. et al. Experimental Tunneling Ratchets Science, Vol. 286, Issue 5448, 1999, Figure 1, p. 2314
Ibid., Figure 3, p. 2317
Blau, S. The Unusual Thermodynamics of Microscopic Systems Physics Today, September, 2002, Figure 1, p. 19
Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences Physical Review E, Vol. 60, No. 3, September, 1999, p. 2724
Yater, J.C. Relation of the second law of thermodynamics to the power conversion of energy fluctuations Physical Review A, Vol. 20, No. 4, October, 1979, Figure 1, p. 1614
Ibarra-Bracamontes, et al. Stochastic ratchets with colored thermal noise Physical Review E, Vol. 56, No. 4, October, 1997, Figure 2A, p. 4050
Engel, A., et al. Ferrofluids as Thermal Ratchets Physical Review Letters, Vol. 91, No. 6, 2003, Figure 2, p. 060602-3
Bulsara, A.R. et al. Tuning in to Noise Physics Today, March, 1996, p. 39
Goychuk, I. et al. Nonadiabatic quantum Brownian rectifiers Physical Review Letters, Vol. 81, No. 3, 1998, Figure 1, p. 651
Ibid., Figure 2, p. 651
Valone, Thomas. Harnessing the Wheelwork of Nature: Teslas Science of
Energy. Adventures Unlimited Press, Kempton, 2002, p. 9
Obousy, Richard K. Concepts in Advanced Field Propulsion. University of
Leicester,
Boyer, 1985, p. 77
Isaev, P. S. Quantum Electrodynamics at High Energies. American Institute of
Physics, NY, 1989, p.86
Rueda, A. and Bernard Haisch. Electromagnetic Zero Point Field as Active Energy
Source in the Intergalactic Medium. 35th AIAA/ASME/SAE/ASEE Joint Propulsion Conference. June 20, 1999, AIAA paper #99-2145, p. 4
Puthoff, Harold. Gravity as a zero-point-fluctuation force. Physical Review A.
Vol. 39, No. 5, March 1989, p. 2336
Isaev, p. 98
Lapedes, Daniel. Dictionary of Physics and Mathematics.
p. 745
Puthoff, 1989, p. 2339
Forward, Robert. An Introductory Tutuorial on the Quantum Mechanical Zero Temperature Electromagnetic Fluctuations of the Vacuum. Mass Modification Experiment Definition Study. Phillips Laboratory Report #PL-TR 96-3004, 1996, p. 3
Milonni, p. 5
Ibid., p. 9
Planck, M. Uber die Begrundung des Gesetzes der scwarzen Strahlung.
Ann. d. Phys. 37, 1912, p. 642
Baym, p. 126
Granger, S., and G.W. Ford. Electron Spin Motion in a Magnetic Mirror Trap,
Phys. Rev. Lett., 5, 1972, p. 1479
Ibid., p.49
Fulcher, L., and J. Rafelski, A. Klein. The Decay of the Vacuum. Scientific American, Dec. 1979, p. 153
Petersen,
1997, p. 89
Lamoreaux, S. K. Demonstration of the Casimir force in the 0.6 to 6 m range. Phys.
Rev. Lett. 78, 5, 1997, p. 1
Zinkernagel, Henrik. High Energy Particles and Reality. Ph.D. Thesis,
University of
Dirac, P. A. M. The Quantum Theory of the Emission and Absorption of
Radiation. Proc. Roy. Soc. Lond. A 114, 1927, p.243
Callen, H. B. and T. A. Welton. Irreversibility and Generalized Noise. Phys. Rev.
83, 1951, p. 34
Nyquist, H. Thermal Agitation of Electric Charge in Conductors. Phys. Rev. 32, 1928,
p. 110
Callen et al., p. 34
Ibid., p. 34
Feynman, Richard. The Feynman Lectures on Physics, Volume II. Addison-Wesley,
Ibid., p. 38
Yam, Philip. Exploiting Zero-Point Energy. Scientific American. December,
1997, p. 82
Forward, Robert. Extracting electrical energy from the vacuum by cohesion of
charged foliated conductors. Phys. Rev. B. 30, 4, 1984, p.1700
Obousy, Richard K., Appendix
Barrow, John. The Book of Nothing.
Pantheon Books,
Mann, Charles. Getting Over Oil. Technology Review. Jan-Feb., 2002, p. 33
Deffeyes, Kenneth. Hubberts Peak: The Impending World Oil Shortage.
Brown, Lester, and Christopher Flavin, Hilary French. The State of the World,
Worldwatch Institute, Washington, 1999, p.26
Greer, Steven. Disclosure: Implications for the Environment, World Peace,
World Poverty and the Human Future. Disclosure Project Briefing Document, The Disclosure Project, April, 2001, p. 2
Haisch, Bernard, and Alfonso Rueda, Harold Puthoff. Inertia as a zero-point-
field Lorentz force. Physical Review A. Vol. 49, No. 2, Feb., 1994, p. 678
Clarke, Arthur C. 3001, The Final Odyssey. Ballantine Books, NY, 1997, p. 245
Planck, M., p. 642
Milonni, p. 10
Einstein, A. Zur gegenwartigen Stand des Strahlungsproblems. Phys. Zs. 10,
1909, p. 185
Ibid., p. 19
Einstein, A. and O. Stern. Einige Argumente fur die Annahme einer molekularen
Agitation beim absoluten Nullpunkt. Ann. d. Phys. 40, 1913, p. 551
Dirac, P. A. M. The Quantum Theory of the Emission and Absorption of
Radiation. Proc. Roy. Soc. Lond. A 114, 1927, p. 243
Dirac, P. A. M. The Quantum Theory of the Electron. Proc. Roy. Soc. Lond.
A117, 1928, p. 610
Debye, P. Interferenz von Rontgenstrahlen und Warmebewegung. Ann. d.
Phys. 43, 1914, p. 49
Wu, T. Y. The Physical and Philosophical Nature of the Foundation of Modern
Physics. Linking Pub. Co.,
Pauling, L. and E. B. Wilson, Introduction to Quantum Mechanics.
1935, p. 74
Pauli, Wolfgang. Selected Topics in Field Quantization.
Snow, T. P. and J. M. Shull. Physics,
West Pub. Co.,
Halliday, D., and R. Resnick, Physics Part II. John Wiley & Sons, NY, 1967, p. 1184
Einstein, A., 1917, p.121
Snow et al., p. 877
Isaev, p. 4
Ibid., p. 33
Casimir, H. B. G. On the attraction between two perfectly conducting plates.
Proc. K. Ned. Akad. Wet. 51, 1948, p. 793
Sparnaay, M.J. 'Measurements of Attractive Forces between Flat Plates,'
Physica (
Lamoreaux, S. K. Demonstration of the Casimir force in the 0.6 to 6 m range.
Phys. Rev. Lett. 78, 5, 1997, p. 1
Browne, Malcolm. Physicists confirm power of nothing, measuring force of
quantum foam. The New York Times. January 21, 1997, p. C1
Puthoff, Harold. Ground State of Hydrogen as a Zero-Point Fluctuation-
Determined State. Phys. Rev. D 35, 1987, p. 3266
Isaev, p. 15
Hawton, Margaret. One-photon operators and the role of vacuum fluctuations in the
Casimir force. Phys. Rev. A. 50, 2, 1994, p. 1057
Milonni, p. 80
Forward, 1984, p. 1700
Iacopini, E. Casimir effect at macroscopic distances. Phys. Rev. A. 48, 1,
1993, p. 129
Weigert, Stefan. Spatial squeezing of the vacuum and the Casimir effect.
Phys. Lett. A. 214, 1996, p. 215
Lambrecht, Astrid, and Marc-Thierry Jaekel, Serge Reynaud. The Casimir force for passive mirrors. Phys. Lett. A. 225, 1997, p. 193
Cougo-Pinto, M. V. Bosonic Casimir effect in external magnetic field. J. Phys. A: Math. Gen. V. 32, 1999, p. 4457
Pinto, F. Engine cycle of an optically controlled vacuum energy transducer. Phys. Rev. B. V. 60, No. 21, 1999, p. 14740
Liu, Z. and L. Zeng, P. Liu. Virtual-photon tunnel effect and quantum noise in a one-atom
micromaser. Phys. Lett. A. V. 217, 1996, p. 219
Valone, Thomas. Inside Zero Point Energy. Journal of New Energy. Vol. 5, No. 4, Spring, 2001, p. 141
Yater, Joseph. Relation of the second law of thermodynamics to the power conversion of energy fluctuations. Phys. Rev. A. Vol. 20, No. 4, 1979, p. 1614
Yater, Joseph. Rebuttal to Comments on Power conversion of energy fluctuations. Phys. Rev. A. Vol. 20, No. 2, 1979, p. 623
Barber, Bradley P., and Robert Hiller, Ritva Lofstedt, Seth Putterman, Keith Weninger, Defining the Unknowns of Sonoluminescence. Physics Reports. 281 (2), March, 1997, p. 69
Eberlein, Claudia. Sonoluminescence as Quantum Vacuum Radiation. Phys. Rev. Lett. V. 76, No. 20, 1996, p. 3842
Liberati, S., and M. Visser, F. Belgiorno, D. Sciama. Sonoluminescence as a QED vacuum effect: probing Schwingers proposal. J. Phys. A: Math. Gen. 33, 2000, p. 2251
Haisch, et al., 1994, p. 678
Feigel, A. Quantum vacuum contribution to the momentum of dielectric media. Physical Review Letters, Vol. 92, p. 020404, 2004
Cole, Daniel, and Harold Puthoff. Extracting energy and heat from the vacuum. Physical Review E. Vol. 48, No. 2, August, 1993, p. 1562
Puthoff, Harold, and S. R. Little, M. Ibison. Engineering the zero-point field and polarizable vacuum for interstellar flight. Journal of the British Interplanetary Society. Vol. 55, 2002, p.137
Ibid., p. 137
Ibid., p. 4
Milonni, 1994, p. 111
Casimir, 1948, p. 793
Boyer, 1980, p. 66
Milonni, 1994, p. 19
Puthoff, 1989, p. 233
Puthoff, 1987, p. 3266
Haisch et al., 1994, p. 678
Lamb, 1947, p. 241
Baym, 1978, p. 99
Planck, p. 642
Callen et al., p. 34
Eberlein, p. 842
Milonni, 1994, p. 111
Baym, p. 126
Milonni, 1994, p. 99
Boyer, p. 790
Lamoreaux, p.2
Forward, 1984, p. 1701
Dierauf and Court. Unified Concepts in Applied Physics. Prentice-Hall, 1979, p. 82
Stevens, R. E., and P. K. Sherwood. How to Prepare a Feasibility Study. Prentice-Hall, 1982
A feasibility study: Can you manage it? November 01, 2002 ZDNet
https://www.zdnet.com.au/newstech/hr/story/0,2000024989,20269565,00.htm
Ozaki, S., and R. Palmer, M. Zisman, and J. Gallardo. Feasibility Study-II of a Muon-Based
Neutrino Source 2001, https://www.cap.bnl.gov.mumu/studyii/FS2-report.html
The Feasibility Study November 2002 Nonviolent Peaceforce.
https://www.nonviolentpeaceforce.org/research/summary.htm
Cox, Larry T. Calculation of Resonant Values of Electromagnetic Energy Incident Upon Dielectric Spheres Phillips Laboratory, Air Force Material Command, PL-TR-93-3002, February, 1994, p. 7
Seto, William W. Schaums Outline Series of Mechanical Vibrations. Schaum Pub. Co., New York, 1964, p.22
Morse, Philip M. and Herman Feshbach. Methods of Theoretical Physics, Part II, McGraw-Hill, New York, 1953, p.1066
Sun, Yugang, et al. Shape-Controlled Synthesis of Gold and Silver Nanoparticles Science, Vol. 298, No. 5601, December 13, 2002, p. 2176
Metz, Clyde R. Schaums Outline Series: Theory and Problems of Physical Chemistry, 2nd edition, McGraw-Hill, New York, 1989, p. 435
Table of Periodic Properties of the Elements WLS-18806, Sargent-Welch VWR International, Buffalo Grove, IL, 2002, Side 2
Gautreau, R. and W. Savin. Schaums Outline Series, Theory and Problems of Modern Physics, McGraw-Hill, New York, 1978, p. 107
Duderstadt, James and L.. Hamilton, Nuclear Reactor Analysis, J. Wiley & Sons, New York, 1976, p. 53
Weisskopf, Victor Recent developments in the theory of the electron Reviews of Modern Physics, Vol. 21, No. 2, April, 1949, p. 309
Brink, G. O., Nonresonant Ion Trap Review of Scientific Instruments, Vol. 46, No. 6, June, 1975, p. 739
Pinto, F. Engine cycle of an optically controlled vacuum energy transducer Physical Review B, Vol. 60, No. 21, 1999, p. 14740
Falomir, H., et al. Divergencies in the Casimir energy for a medium with realistic ultraviolet behaviour J. Phys. A Math. Gen. V. 34, August 17, 2001, p. 6291
Brevik, I. Casimir Effect in Dielectrics: On the Low-Frequency Contributions Casimir Forces Workshop: Recent Developments in Experiment and Theory, Harvard University, November 14-16, 2002, p.1
Liu, Z. et al. Virtual-photon tunnel effect and quantum noise in a one-atom micromaser Physics Letters A, V. 217, 1996, p. 219
Cheng, H. The Casimir energy for a rectangular cavity at finite temperature J. Phys. A: Math Gen. Vol. 35, March 8, 2002, p. 2205
Klimchitskaya, G. Problems with the Thermal Casimir Force between Real Metals Casimir Forces Workshop: Recent Developments in Experiment and Theory, Harvard University, November 14-16, 2002, p.1
Dodonov, V.V. Resonance photon generation in a vibrating cavity J. Phys. A Gen. V. 31 Dec. 11, 1998, p. 9835
Andreata, M.A. Energy density and packet formation in a vibrating cavity J. Phys. A: Math. Gen. V. 33, April 28, 2000, p. 3209
Hu, Z. et al. Squeezed Phonon States: Modulating Quantum Fluctuations of Atomic Displacements Phys. Rev. Lett. V. 76, 1996, p. 2294
Dodonov, V.V. et al. Squeezing and photon distribution in a vibrating cavity J. Phys. A: Math Gen. V. 32, 1999, p. 6721
Ford, L.H. et al. Focusing Vacuum Fluctuations Casimir Forces Workshop: Recent Developments in Experiment and Theory, Harvard University, November 14-16, 2002, p. 1
Zheng, M-S., et al. Influence of combination of Casimir force and residual stress on the behaviour of micro- and nano-electromechanical systems Chinese Physics Letters, V. 19, No. 6, 2002, p. 832
Sperry, M. et al. The role of the Casimir effect in the static deflection and stiction of membrane strips in microelectromechanical systems (MEMS) Journal of Applied Physics, V. 84, No. 5, 1998, p. 2501
Maclay, J. Unusual properties of conductive rectangular cavities in the zero point electromagnetic field: resolving Forwards Casimir energy extraction cycle paradox Proceedings of Space Technology and Applications International Forum (STAIF), Albuquerque, NM, January, 1999, p. 3
Maclay, J., et al. Of some theoretical significance: Implications of Casimir effects European Journal of Physics, Vol. 22, 2001, p. 6
Brevik, I. et al. Casimir problem of spherical dielectrics: Numerical evaluation for general permittivities Phys. Rev. E, Vol. 66, 2002, p. 26119
Eberlein, C. Fluctuations of Casimir forces on finite objects. I. Spheres and hemipheres, II. Flat circular disk J. Phys. A: Math. Gen. Vol. 25, 1992, p. 3015
Cognola, G. et al. Casimir energies for spherically symmetric cavities J. Phys. A: Math. Gen. Vol. 34, 2001, p. 7311
Cheng. H. The Casimir energy for a rectangular cavity at finite temperature J. Phys. A: Math. Gen. Vol. 35, 2002, p.2205
Sokolov, I. The Casimir effect as a possible source of cosmic energy Physics Letters A, Vol. 223, 1996, p. 163
Hizhnyakov, V.V. Quantum emission of a medium with a time-dependent refractive index Quantum Optics, Vol. 4, 1992, p. 277
Bohm, D. and J.P. Vigier Model of the Causal Interpretation of Quantum Theory in Terms of a Fluid with Irregular Fluctuations Phys. Rev. Vol. 96, No. 1, 1954, p. 208
Froning, H.D. and R.L. Roach Preliminary simulations of vehicle interactions with the quantum vacuum by fluid dynamic approximations Proceedings of 38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, July, 2002, AIAA-2002-3925, p. 52236
Scully, M.O. et al. Extracting work from a single heat bath via vanishing quantum coherence Science, Vol. 299, Issue 5608, 2003, p. 862
Allahverdyan, A.E. and T.M. Nieuwenhuizen Extraction of work from a single thermal bath in the quantum regime Physical Review Letters, vol. 85, No. 9, August, 2000, p. 1799
Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences Physical Review E, Vol. 60, No. 3, September, 1999, p. 2725
Yater, J.C. Power conversion of energy fluctuations Physical Review A, Vol. 10, No 4, October, 1974, p. 1361
Yater, J.C. Rebuttal to comments on Power conversion of energy fluctuations Physical Review A, Vol. 20, No. 2, August, 1979, p. 623
Yater, J.C. Relation of the second law of thermodynamics to the power conversion of energy fluctuations Physical Review A, Vol. 20, No. 4, October, 1979, p. 1614
Yater, J.C. Reversible Thermoelectric Power Conversion of Energy Fluctuations Proceedings of the Second International Conference on Thermoelectric Energy Conversion, Arlington, Texas, IEEE No. 78CH1313-6, 1978, p. 107
Ibarra-Bracamontes, et al. Stochastic ratchets with colored thermal noise Physical Review E, Vol. 56, No. 4, October, 1997, p. 4048
Engel, A., et al. Ferrofluids as Thermal Ratchets Physical Review Letters, Vol. 91, No. 6, 2003, p. 060602-1
Goychuk, I. et al. Nonadiabatic quantum Brownian rectifiers Physical Review Letters, Vol. 81, No. 3, 1998, p. 649
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3532
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved