| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
THERMAL PROPERTIES OF SOLIDS
The most important thermal parameters of solids are: the specific heat, the thermal conductivity, the thermal expansion (dilatation) coefficient a.o. We will study here the quantum theory of the specific heat. As we will find here, the main contributions to the internal energy (and to the specific heat, implicitly) of solids are due to the crystalline lattice vibrations and to the free electrons, respectively.
Owing to the very different acoustic impedances of the studied solid sample (specimen) and of its surrounding medium, the vibrations of the crystalline lattice lead to standing waves, the opposite faces of the parallelepipedic sample having the same (node or of maximum amplitude) character.
1.The spectral density of the number of independent standing waves
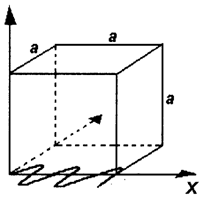 In order to simplify the next calculations, we will consider
a cubic solid specimen, of side a (see Fig.1).
In order to simplify the next calculations, we will consider
a cubic solid specimen, of side a (see Fig.1).
If the cube faces correspond to maxima of the standing waves, the time t and the x,y,z coordinate dependencies of the displacements u can be written as:
![]() , (1.1)
, (1.1)
where ![]() are the components of
the wavevector
are the components of
the wavevector ![]() . Due to the boundary conditions:
. Due to the boundary conditions: ![]() , (1.2) Fig. 1
, (1.2) Fig. 1
one obtains: ![]() and:
and: ![]() , (1.3)
, (1.3)
where ![]() are arbitrary
(negative or positive) integers.
are arbitrary
(negative or positive) integers.
It results the quantization of the standing waves:
![]() , (1.4)
, (1.4)
 where:
where:
![]() . (1.5)
. (1.5)
Because
the negative values (![]() ) of the quantum numbers
) of the quantum numbers ![]() correspond to phase
jumps, but not to different standing waves (1.1), it results that the number
correspond to phase
jumps, but not to different standing waves (1.1), it results that the number ![]() of the different
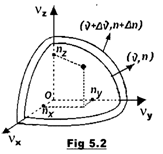
standing waves of frequencies between
of the different
standing waves of frequencies between ![]() and
and ![]() , corresponds to the number of points with positive integer
coordinates in the space of real numbers
, corresponds to the number of points with positive integer
coordinates in the space of real numbers ![]() (see Fig.2).
(see Fig.2).
Taking
into account that one can build a cube of side 1 around each point of integer
coordinates and these cubes (of volume 1) fill without holes or crossings the
crown between the spheres of radii n and n+![]() n (where, according to relation (1.4):
n (where, according to relation (1.4): ![]() ), one finds that:
), one finds that:
![]()
![]() . (1.6)
. (1.6)
Finally one finds that the volume
spectral density of the number of independent
wave states is: ![]() , (1.7)
, (1.7)
where V is the phase speed of the considered waves.
2. The quantum (Debye's) theory of the contribution of crystalline lattice vibrations to the internal energy of solids
Taking into account that to each wave
propagation direction (Oz) there correspond 2 independent (along the Ox and Oy
axes) transverse waves and a (third) longitudinal one (see Figure 3), it
results that the total volume spectral density of the number of independent wave states is: ![]() , (2.1)
, (2.1)
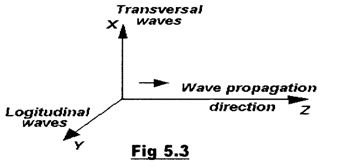
where ![]() and
and ![]() are the phase speeds
of the transverse and longitudinal waves, respectively.
are the phase speeds
of the transverse and longitudinal waves, respectively.
Because the total number of
vibrations (wave modes) of a crystalline lattice with N nodes is equal to 3N-6,
one can deduce the maximum frequency ![]() of the standing waves of this solid (of volume
of the standing waves of this solid (of volume ![]() ) starting from the expression:
) starting from the expression:
![]() .
.
For usual solid sample: N>>1, therefore one obtains:
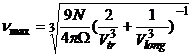 . (2.2) Taking
into account that the sound waves are quantized similarly to the
electromagnetic waves, and their quanta - the phonons satisfy the same quantum
(Bose-Einstein) distribution as the photons, it results that the contribution
of the vibration modes (of frequencies between
. (2.2) Taking
into account that the sound waves are quantized similarly to the
electromagnetic waves, and their quanta - the phonons satisfy the same quantum
(Bose-Einstein) distribution as the photons, it results that the contribution
of the vibration modes (of frequencies between ![]() and
and ![]() ) of the crystalline lattice nodes to the internal energy of
the considered solid sample can be expressed by means of the average occupation
number
) of the crystalline lattice nodes to the internal energy of
the considered solid sample can be expressed by means of the average occupation
number ![]() of the energy
states h
of the energy
states h![]() by bosons as:
by bosons as: 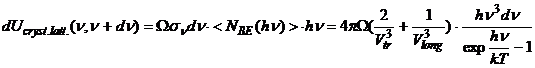 . (2.3)
. (2.3)
Using the symbols: ![]() and:
and: ![]() (the Debye's
temperature), the total contribution of the vibration modes of the crystalline
lattice nodes to the internal energy of the considered solid sample can be
written as:
(the Debye's
temperature), the total contribution of the vibration modes of the crystalline
lattice nodes to the internal energy of the considered solid sample can be
written as:
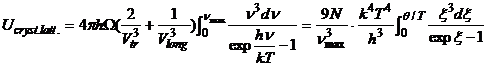 . (2.4)
. (2.4)
Defining the Debye's function as: ![]() , (2.5)
, (2.5)
one can write
the contribution of the crystalline lattice vibrations to the internal energy
of a solid sample including ![]() moles as:
moles as:
![]() . (2.6)
. (2.6)
For relatively high work temperatures (T>>![]() , therefore
, therefore ![]() and:
and: ![]() ), the asymptotic expression of the Debye's function is:
), the asymptotic expression of the Debye's function is:
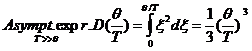 , (2.7)
, (2.7)
therefore the corresponding asymptotic expression of the contribution of the crystalline lattice vibrations to the internal energy of the considered solid sample is:
![]() , (2.8)
, (2.8)
which coincides with the experimental Dulong and Petit law (that agrees also with the theoretical results of the classical Statistical Physics).
Conversely, for relatively low work temperatures (T<<![]() ), the Debye's function tends to the limit:
), the Debye's function tends to the limit: 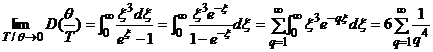 . (2.9)
. (2.9)
Problem 1: Deduce the values of the sums 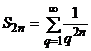 .
.
Solution: Starting from the series expansion of the complex variable function z.cotan z (see e.g. Th.Angheluta 'Course of the theory of complex variable functions' (in Romanian), Ed.Tehnica, 1957, p. 244-46 or V.I.Smirnov 'Course of higher mathematics' (in Romanian),vol.II, Ed.Tehnica,1954,p.440-41):
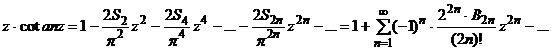 , where the Bernoulli's numbers
, where the Bernoulli's numbers ![]() are defined by the
series expansion:
are defined by the
series expansion:
![]() ,
,
which implyes
the recurrence relation with the symbolic expression: ![]() . (2.10)
. (2.10)
From the recurrence relations for n =2, 3, 4 and 5:
![]()
![]() and:
and: ![]() , one obtains successively the values:
, one obtains successively the values: ![]() and:
and: ![]() .
.
Comparing the expressions of the
general terms from the 2 series expansions of the function z.cotanz, one
obtains: ![]() , (2.11)
, (2.11)
therefore for n =2: ![]() . (2.12)
. (2.12)
The recurrence relation (2.10)
allows the successive determination of Bernoulli's numbers ![]() and
and ![]() for n =3, n =4 a.s.o., while the
relation (2.11) will lead to the corresponding expressions of the sums
for n =3, n =4 a.s.o., while the
relation (2.11) will lead to the corresponding expressions of the sums ![]() .
.
From relations (2.6),(2.9) and (2.12), it results the asymptotic expression - for relatively low work temperatures (T<<q ) - of the contribution of the crystalline lattice vibrations to the internal energy of the considered solid sample:
![]() . (2.13)
. (2.13)
Problem 2: Starting from the values of the
longitudinal (Young) and shear elasticity moduli, respectively: ![]() and
and ![]() for copper (A=63.54,
for copper (A=63.54, ![]() ), determine: a) the Poisson's coefficient
), determine: a) the Poisson's coefficient ![]() , as well as the propagation velocities of longitudinal and
shear sound waves, respectively, in copper; b) the maximum frequency
, as well as the propagation velocities of longitudinal and
shear sound waves, respectively, in copper; b) the maximum frequency ![]() of the crystalline
lattice vibrations (of phonons) and the Debye's temperature of the copper.
of the crystalline
lattice vibrations (of phonons) and the Debye's temperature of the copper.
Solution: a) From the
relations: 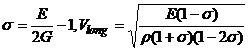 and:
and: 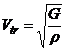 ,
,
one obtains: ![]() .
.
b) The number of copper atoms in the volume unit of the considered rod is:
![]() .
.
Finally, one finds:
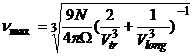
![]() and:
and: ![]() .
.
3.The quantum (Debye) theory of the contribution of the crystalline lattice vibrations to the specific heat of solids
Starting from the definition of the molar
specific heat and neglecting the dilatation of solids, one finds: ![]() . (3.1)
. (3.1)
Using the relations (2.7) and (2.13), one obtains the asymptotic quantum (Debye) expressions of the crystalline lattice contributions to the specific heat of solids.
a) The case of relatively high work temperatures (T>>![]() ):
):
![]() .
.
One finds that this result coincides
with the classical expression (the Dulong
and Petit's law) of the molar specific heat. It results that the contribution of the crystalline lattice
vibrations to the specific heat prevails at high work temperatures (T>>![]() ).
).
b) The case of relatively low work temperatures (T<<![]() ):
):
![]() .
.
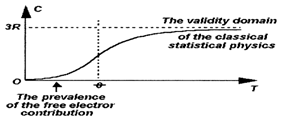
Because
the contribution of the free electrons to the specific heat of a solid
increases linearly with its temperature (see chapter 7), it results that the
free electron contribution prevails at very low temperatures (see Figure 4).
Fig. 4
REFERENCES
Ch.Kittel
Introduction to
Gh.Zet,
D.Ursu Condensed Matter Physics. Applications in Engineering (in Romanian),
Technical Publishing House,
C.Motoc Condensed Matter Physics,
Univ.Politehnica Publ. House,
Ion
Munteanu Condensed Matter Physics (in Romanian), 1st part,
Hyperion Publishing House,
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2303
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved