| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
Mathematics has long played a role in design. Straight lines, circles and squares are made-made devices; they make no appearance in nature. In many ways, mathematics is an ideal model of the physical, showing how systems perform under perfect circumstances. Nothing in the physical world is perfect, however, so one can only use math as a model to show how things should act. Design imposes no limits of nature on its creators. Straight lines can exist in the artists world. Does the ideal setting of mathematics play a role creating appealing design? In this paper, I will attempt to answer this question by examining two works of Dutch architect and designer Gerrit Rietveld.
The work of Rietveld is very representative of the De Stijl group. Simplicity is one key ingredient in Rietvelds work, I will attempt to parallel this with simplicity in mathematics with an analysis of the red-blue chair. Additionally, most art from the De Stijl movement uses very strong vertical and horizontal lines [7]. I will investigate the geometric implication of these lines, and relate that to algebra. To conclude my analysis of the red-blue chair, I will show the appeal of its grid oriented design. Since most of this analysis also directly relates to the Schrder house, I will explain the beauty of the basic building blocks in the Schrder house. I feel that the Schrder houses exterior vertical and horizontal lines have a direct correlation to representing integers as prime numbers, hence I will discuss the house in this setting.
In 1918, Gerrit Rietveld designed a now legendary chair. Its a simple enough chair, making use of elementary construction techniques [9]. Rietvelds red-blue chair can be constructed from a few rails and two pieces of plywood for the back and seat. This simplicity is intentional, as Rietveld sought to relieve the craftsman of the dull, repetitive task of creating similar furniture for many clients [2].
|
|
|
Figure 1. Rievelds 1918 masterpiece, the red-blue chair [8]. |
This simple design has connections to mathematics is many ways. A common goal of mathematics is to simplify nature. Consider the problem of modeling an oil spill in the artic tundra. Its certainly beneficial to know how far the oil will spread, so its natural to wish to model the spread of the oil with a mathematical model. The model one uses to do this is so simplified that its possible to calculate how far the oil will spread by hand. Imagine if we had to run a computer simulation to model each drop of oil interacting with each rock in the soil. Wed never find an answer.
Rietveld used simplicity to his advantage. He didnt overdo it, just as our model of an oil spill cant be too simple. Reitvelds red-blue chair is simple, however its not a seat with a backrest attached. The chair has rails that serve little function besides aesthetic beauty. This simplification, without oversimplification is one factor that has led to the widespread appeal of the red-blue chair.
The red-blue chair also has connections to standard Euclidean geometry. An image of the joining of three rods in the chair is seen in Figure 2.a. Rietveld intentionally designed the joints in this manner to indicate the truncation of their virtual extension on the three space axes into un endlessness [6]. In other words, he wanted each rod to appear to extend infinitely. I feel that the seemingly endless extension of these rods appeals to the human senses. They make the chair seem huge, infinite in dimension. The lines of the chair extend past our vision and subconsciously expand forever. Adding universal appeal, the mathematics behind this is taught to high school students around the world.
|
a.
|
b. |
|
Figure 2. Comparing the joints of the Red Blue chair with the standard 3-axis Cartesian coordinate system. |
|
To understand the geometry, and the endless expansion of the rods, the Cartesian coordinate system comes into play, which is a fancy name for the simplest way to graph a function on paper. In Figure 2.b, the 3-dimensional coordinate system is drawn. Or a section of the coordinate system. In theory, the lines drawn in Figure 2.b should continue on indefinitely, theyre infinite as geometric space is boundless. Interpreting Rietvelds rod junction as a mathematical object yields what is known as a vector space, which is simply a more abstract representation of the Cartesian coordinate system. It says points in 3-dimesional space can be written like this
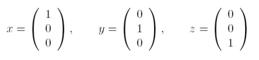
See, the x represents the magnitude of the line along the x-axis, the y the magnitude along the y-axis and similarly for z. In a way, the joints in Rietvelds chair represent this abstraction. I feel that the appeal of Rietvelds chair in many ways is a representation of the beauty of this abstraction. To a mathematician, some theories and results are beautiful because of the way they view a problem. The red-blue chair represents this beauty in a tangible form.
In addition to showing how we can create the entire 3-dimensional space, the red-blue chair plays nice within the confines of its defined unit. Rietveld designed the red-blue chair using a grid. Have a look
|
|
|
Figure 3. The major lines in the red-blue chair follow a 10 cm by 10 cm grid. |
When we juxtapose a 10 cm by 10 cm grid and the red-blue chair, we see that the major lines of the red-blue chair conform nicely to this grid. This also plays a role in differentiating between sets of numbers.
While defining different sets of numbers, lets have an extremely brief history of numbers. The development of numbers came about with the need to calculate. The farmers needed a good method to determine a fair price for a certain amount of a crop. So what is known as the natural numbers was developed. The natural numbers are whole numbers, they look like this N = . For convenience, many mathematicians include zero in the natural numbers, however zero was developed much later, so its incorrect from a historic viewpoint. Next came the integers. The integers are also whole numbers, but also negative whole numbers and zero. Integers look like this Z = . Theres a problem, however. When we divide 5 by 3, we cant represent the result as an integer. This brought about the development of the rational numbers. Rational numbers are simply an integer that is divided by another integer. This means we can represent numbers as fractions, like x/y as long as x and y are both integers. And one more number set to know is the real numbers. Real numbers are numbers like π that have never-ending decimals, so any number what a non-repeating decimal that never ends is a real number, not a rational number, since we cant write it as a fraction. All integers and rationals are included in the real numbers. Theres a lot of real numbers; and as counter-intuitive as it seems, there is the exact same number of integers and rationals, but there is infinitely more real numbers than integers or rationals. Now we have an idea of what integers, rational numbers and real numbers are from an algebraic point of view. However, what are they from a geometric point of view? Have a look at Figure 4 below.
|
|
|
Figure 4. An integer grid superimposed on the Cartesian plane. |
The dots at the line intersections in Figure 4 represent the integers. The space between represents the real numbers. If we only allowed numbers to be represented as dots, wed miss a lot of numbers between the dots, infinitely many numbers actually. Hence, weve ran into the same wall as mathematicians before the real numbers.
The beauty of integers over their real number counterparts is portrayed in the red-blue chair by its conformance to a grid design. In math terms, the rods in the red-blue chair are integers. Some of the power and striking beauty of the red-blue chair stems from the even spacing of its rods. I feel the even, integer spacing of the red-blue chairs major lines is an important element of its appeal. Integers are more natural than real numbers, and the same holds true for the alignment of rods in the red-blue chair.
In all, the three major mathematical ideas used in the design of the red-blue chair are simplification, infinitely extending lines that represent the Cartesian plane and the grid layout of its major vertical and horizontal lines. All three of these ideas are viewed as beautiful in mathematics as well. I feel that their universal like qualities make the red-blue a widespread sensation, a chair that is considered beautiful around the world.
While Rietveld began his career as a furniture designer, he found himself working as an architect later on. In 1924, Rietveld designed a house for Mrs. Schrder, now commonly referred to as the Schrder house [1, 10]. Much of the previous mathematical analysis of the red-blue chair is applicable to the Schrder house as well, since the design follows a similar mantra. However, the outside of the Schrder does not follow the a grid design such as the red-blue chair. I will focus my analysis of the Schrder by relating the components of its design to prime integers.
|
|
|
Figure 5. The Schrder house [8]. |
Prime numbers are special numbers. Their importance was realized as long ago by Greek mathematicians [4]. So whats a prime? A prime number is an integer bigger than one that is only divisible by itself and one. When I say divisible, I should clarify that this means cleanly divisible, no remainder is allowed. A few of the first prime numbers are 2, 3, 5, 7, 11, 13, 17, and 19. It turns out that the prime numbers are the building blocks of the integer. In The Elements, a treatise on mathematics by the Greek mathematician Euclid, he proves that all integers can be written as the multiple of one or more primes [5]. So, we can represent any integer by a list of its prime factors, the primes that construct this integer. For example, 6 = 3 and 35 = 7 and 1386 = 11.
Surprisingly enough, I feel that prime factorizations relate to the Schrder house. Looking at the outside of the Schrder house (Figure 5), one feels that there is an underlying theme. Everything on the outside of the Schrder house is either a vertical or a horizontal line. To me, vertical and horizontal lines are the building blocks of all De Stijl movement art. I compare these with the prime numbers as the building blocks of nature.
This appeals to the human sense in many ways. Its pleasant to think of all underlying forces in the universe as being constructed of some principal element. Its an appealing notion to the human psyche. The vertical and horizontal lines of the Schrder house appeal to the same sense as the prime numbers. The beauty and simplicity of both give each a rare allure.
As an aside, I would like to mention that both art and mathematics have progressed. Mathematicians later developed numbers that the primes cant construct like the rational numbers and artists moved on from the primal vertical and horizontal lines. However, as citizens of the 21st century, we still see the inherent beauty of each.
In this paper, I have taken the position that Rietvelds red-blue chair and Schrder house are appealing universally due to their inherent mathematical representations. Mathematics has played a role in design for centuries, beginning with perspective. I feel Rietvelds work is a continuation of beautiful art that is created with mathematical ideas lurking in the shadows. Did Rietveld feel that he was representing the prime numbers with his strong vertical and horizontal lines? Most likely not, but viewed in this light, we can further understand the appeal of art that has been reduced to primitive vertical and horizontal lines.
I feel that simplicity and the grid-adhering layout of the red-blue chair are two key elements in its appeal. I have shown how these two concepts are related to the study of mathematics. In the analysis of the Schrder house, I chose only to focus only on the exterior, comparing the strong vertical and horizontal lines with the building blocks of the integers, prime numbers. While its impossible for all art constructed of prime vertical and horizontal lines to have widespread appeal, Rietveld used these prime elements to create an amazing house. So too, can mathematicians use prime numbers to do amazing work, such as secure internet transactions.
So does mathematics play a role in appealing design? I feel strongly towards the positive. However, mathematics does not make great art. Artists, designers and architects must use elements carefully to craft beautiful objects; mathematics alone does not birth an inspired painting. Art has universal appeal for many reasons, and I feel that the mathematics in art is one such reason.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3401
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved