| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
1) GENERALITES.
Nous avons étudié dans le chapitre précédent lAnneau des polynômes à
une indéterminée à coefficients dans un corps commutatif K infini et de caractéristique nulle.
On a vu en particulier que cet Anneau est commutatif et intÃgre, au sens quun produit ne peut y Ãtre nul que si au
moins un de ses facteurs est égal au zéro de cet Anneau.
Il existe un processus algébrique standard permettant dans une telle
configuration détendre cette structure dAnneau en une structure de corps
commutatif appelé corps des fractions
de lAnneau en question.
Ce processus permet par exemple de construire le corps classique des nombres
rationnels à partir de lAnneau des entiers relatifs.
Appliqué à notre Anneau K[X] des polynômes sur K il va nous conduire au corps des fractions rationnelles
à coefficients dans K que nous noterons K(X).
On se propose dans ce nouveau chapitre danalyser le procédé de construction et
les commodités apportées à la théorie par lintroduction de cette
extension.
A) Définitions.
1)
Fraction rationnelle.
Soit (A, B) un couple déléments de K[X] avec B non identiquement nul. On appelle fraction rationnelle de représentant (A, B),
lensemble formé par tous les couples (P, Q) de polynômes à coefficients
dans K tels que A.Q=B.P et Q non identiquement nul.
On adoptera lécriture ![]() pour représenter cette
fraction.
pour représenter cette
fraction.
Une fraction rationnelle apparait donc comme un collectif défini à
partir dun couple initial.
Remarquons alors que si (C, D) est un couple tel que A.D=B.C et D non nul, la
fraction rationnelle de représentant (C, D) coÃncide exactement avec la
fraction de représentant (A, B)
En effet, si C.Q=D.P on en déduit en multipliant par P : B.C.Q=B.D.P ,
puis A.D.Q=B.D.P daprÃs la relation liant (A,B) à (C,D), et
enfin A.Q=B.P en simplifiant par D non nul, vu lintégrité de K[X]. On déduit de mÃme C.Q=D.P à partir de
A.Q=B.P en multipliant par D puis en simplifiant par B non nul.
Chacun des couples (P,Q) tels que A.Q=D.P et Q non nul mérite donc aussi le nom
de représentant de la fraction et on pourra écrire F=![]() .
.
P et Q seront appelés respectivement numérateurs et dénominateurs du
représentant (P,Q).
2)
Représentant irréductible.
Si de plus P et Q nont pas dautres diviseurs communs que les polynômes
constants, le représentant (P, Q) sera dit irréductible.
La connaissance dun représentant irréductible permet
dobtenir facilement tous les autres représentants de la fraction considérée
comme lindique le résultat suivant :
Si (A, B) est un représentant irréductible de F, alors (P, Q) est un représentant de F si et seulement si il existe un polynôme l non nul tel que P=lA et Q=lB.
_ La condition est évidemment
suffisante puisque (lA).B=(l.B).A
_ Réciproquement, supposons A.Q=B.P avec (A,B) irréductible. On a vu en fin du
chapitre précédent, en application de lAlgorithme dEuclide, lidentité de
Bezout assurant lexistence dun couple (U, V) de polynômes tel que A.U+B.V=1
On en déduit P=P.A.U+P.B.V=P.A.U+A.Q.V=(P.U+Q.V).A=l.A avec l=P.U+Q.VIK[X]
De mÃme Q=Q.A.U+Q.B.V=B.P.U+Q.B.V=(P.U+Q.V).B=l.B
Cette propriété permet détablir lunicité des représentants irréductibles, au
produit par une constante prÃs. En effet si (A, B) et (C, D) sont deux
représentants irréductibles dune mÃme fraction F, il existe alors un
polynôme l tel
que C=l.A
et D=l.B
mais également un polynôme a tel que A=a.C et B=a.D. On en déduit B=a l.B
et par suite 1=a l puisque B non nul.
Nécessairement a et l sont donc des polynômes de
degré 0 donc constants.
3)
zéros et pôles dune fraction rationnelle.
La remarque ci-dessus permet de définir sans ambiguÃté les deux notions
suivantes :
Si F=![]() avec (A, B) irréductible, on appelle zéro de F dordre n,
toute racine dordre n du numérateur
A et pôle dordre s de F, toute racine dordre s du dénominateur B.
avec (A, B) irréductible, on appelle zéro de F dordre n,
toute racine dordre n du numérateur
A et pôle dordre s de F, toute racine dordre s du dénominateur B.
Remarquons quun élément a ne peut
Ãtre à la fois zéro et pôle de F, cela entrainerait la
divisibilité de A et B par X-a et
nierait le caractÃre irréductible du représentant.
4)
Fonction rationnelle associée à une fraction rationnelle F de
représentant irréductible (A,B)
On appellera ainsi la fonction f
définie sur le corps K privé de lensemble P(F) des pôles de F, à valeurs dans K et définie par la formule ![]() .
.
Ici encore la définition de f ne
dépend pas du couple irréductible choisi pour définir f, et on remarque également que pour un représentant (P, Q)
quelconque de F, non nécessairement irréductible, on a bien en tout x nétant pas racine de Q : ![]()
Par abus de langage et de notation on dira simplement que f(x) est la valeur en x de
la fraction rationnelle F et on écrira f(x)=F(x).
B) Opérations sur
les fractions.
1)
Définition des opérations fondamentales.
Si ![]() désignent deux
fractions rationnelles données à partir de représentants irréductibles,
on définit la somme et le produit de ces fractions par les égalités :
désignent deux
fractions rationnelles données à partir de représentants irréductibles,
on définit la somme et le produit de ces fractions par les égalités :
![]()
On vérifie immédiatement que les résultats de ces opérations ne dépendent que
des fractions en jeu F et G et non pas des choix arbitraires des
représentants irréductibles choisis pour définir ces mÃmes fractions. En
effet si (P,Q) désigne un représentant quelconque de F et (U,V) un autre représentant de G, on sait quil existe deux polynômes
non nuls, soient a et b tels que P=aA , Q=aB , U=bC et V=bD. On en
déduit immédiatement :
![]()
Les opérations peuvent donc Ãtre définies à partir de
représentants quelconques des fractions, mÃme non nécessairement
irréductibles.
Remarquons que pour tout scalaire x
nappartenant pas à la réunion de lensemble des pôles des deux
fractions F et G, les valeurs en x de F+G et F.G sont tous simplement les
sommes et produits des images respectives au sens des lois sur le corps K. En effet :
![]()
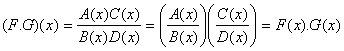
2)
Corps des fractions rationnelles.
On vérifie sans aucune difficultés que lensemble K(X) des fractions rationnelles à coefficients dans K, muni dans lordre des deux lois de composition interne
somme et produit définies ci dessus acquiert une structure de corps commutatif.
(On convient dans ce qui suit de noter par a le polynôme constant aX0).
Lassociativité, la commutativité de + et . , la distributivité du produit
par rapport à la somme sétablissent directement à partir des
définitions mÃmes, en utilisant des représentants quelconques des
fractions considérées.
_ Le neutre pour laddition est la fraction dite nulle, de représentant (0, 1).
_ La symétrique pour la somme de ![]() est la fraction -
est la fraction -![]() appelée opposée de F.
appelée opposée de F.
_ Le neutre pour le produit est la fraction de représentant (1, 1).
_ La symétrique pour le produit de la fraction non nulle ![]() est la fraction
est la fraction ![]() appelée inverse de F et notée
appelée inverse de F et notée ![]() conformément aux notations multiplicatives usuelles.
conformément aux notations multiplicatives usuelles.
3)
Plongement des polynômes dans le corps des fractions.
Le corps K(X) que lon vient de définir contient en fait une trace
de lAnneau des polynômes K[X] situé à la base de
la construction. Pour sen persuader il suffit de considérer lapplication j de K[X] vers K(X) qui associe à
chaque polynôme P la fraction j(P)=![]() .
.
Il est clair que j(P+Q)=j(P)+j(Q)
et j(P.Q)=j(P).j(Q) pour tout
couple (P, Q) de polynômes.
De plus j(X0)=![]() =1 . Lapplication j
est donc un morphisme dAnneau.
=1 . Lapplication j
est donc un morphisme dAnneau.
Il suffit alors de remarquer que j
est injective pour conclure que limage j(K[X]) est un sous-Anneau du corps des fractions isomorphe
à lAnneau originel des polynômes K[X].
Si on convient de noter abusivement j(P)=![]() , la fraction quelconque
, la fraction quelconque ![]() apparait alors comme
le produit effectif de P(X) par linverse de Q(X) et la notation
adoptée ainsi que lappellation corps des fractions se justifient pleinement.
apparait alors comme
le produit effectif de P(X) par linverse de Q(X) et la notation
adoptée ainsi que lappellation corps des fractions se justifient pleinement.
F(X)
est véritablement le quotient du polynôme P(X) par le polynôme Q(X), cest à dire
le produit de P(X) par linverse de Q(X). (En réalité cest ![]() ).
).
4)
Caractérisation des zéros et pôles multiples dune fraction.
On a posé en définition que lélément a
de K est zéro dordre n
dune fraction ![]() donnée sous forme
irréductible si et seulement si a est
racine multiple dordre n de A(X).
donnée sous forme
irréductible si et seulement si a est
racine multiple dordre n de A(X).
Ceci entraine la factorisation du numérateur sous la forme A(X)=(X-a)nC(X) avec C polynôme tel que C(a) non nul. On peut alors écrire F(X)=
(X-a)nG(X) avec G fraction rationnelle définie comme quotient de
C par B , donc nadmettant a ni
pour zéro, ni pour pôle.
Réciproquement considérons une fraction ![]()
fraction nadmettant a ni pour zéro,
ni pour pôle et supposée écrite ici sous forme irréductible.
Si (A1,B1) est un représentant
irréductible de F, on sait quil
existe un polynôme l tel
que :
(X-a)n a(X)=l(X)A1(X) et b(X)=l(X)B1(X).
Puisque a nest pas racine de b, on en déduit que l(a) est non nul et que par suite a
est racine de A1, dordre
nécessairement n car a nest pas non plus racine de a.
Ainsi a est bien zéro dordre n de F
au sens premier. On a donc établi léquivalence :
a zéro dordre n de F F(X)=(X-a)nG(X) avec G fraction dont a nest
ni zéro ni pôle.
Grace à la remarque : a
zéro dordre n de F a pôle dordre n de ![]() , on déduit aussitôt :
, on déduit aussitôt :
a
pôle dordre n de F ![]() avec G fraction dont a nest ni zéro ni pôle.
avec G fraction dont a nest ni zéro ni pôle.
2) DERIVATION FORMELLE.
A)
Définition.
Supposons que lon veuille étendre le processus de dérivation formelle des
polynômes à lensemble des fractions rationnelles, et ceci de façon que
la rÃgle de dérivation des produits soit conservée.
Si ![]() , cest à dire si
, cest à dire si ![]() , on devra donc avoir nécessairement :
, on devra donc avoir nécessairement :
![]() et par suite la
dérivée de F(X) devra Ãtre évaluée suivant
et par suite la
dérivée de F(X) devra Ãtre évaluée suivant
la formule : ![]()
On vérifie facilement que la fraction précédente ne dépend pas du représentant
arbitraire (P, Q) de F.
En effet, si ![]() , on obtient dabord,
en dérivant la relation A.Q=B.P , légalité AQ+AQ=BP+BP
puis en multipliant par BQ, la
formule : ABQ²+ABQQ=BPBQ+B²QP.
, on obtient dabord,
en dérivant la relation A.Q=B.P , légalité AQ+AQ=BP+BP
puis en multipliant par BQ, la
formule : ABQ²+ABQQ=BPBQ+B²QP.
Enfin, en remplaçant BP par AQ à droite et AQ par BP à gauche dans légalité précédente, on obtient facilement : (AB-AB)Q²=B²(PQ-PQ)
qui équivaut à : ![]()
La définition de la dérivée formelle dune fraction F selon la formule encadrée ci dessus est donc sans aucune
ambiguÃté.
On introduit ensuite naturellement comme on la déjà fait pour les
polynômes, les dérivées successives de F
par dérivations en cascade : F(0)=F et nIN F(n+1)=[F(n)]
On vérifie facilement que : a
pôle dordre n de F a pôle dordre n+1 de F , grace à la relation : 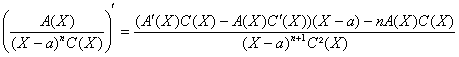
B) RÃgles de
calcul.
On démontre sans peine que les formules de dérivation établies sur les
polynômes pour la somme et le produit sétendent à lidentique sur le
champ des fractions rationnelles.
Ainsi la dérivée dordre n quelconque
dune somme de fractions est la somme des dérivées dordre n de chacune dentre elles, la dérivée dordre n du produit F.G
sobtient conformément à la formule de Leibniz.
Notons les résultats utiles pour la suite, qui sétablissent facilement par
récurrence sur n :
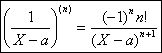 et kIN
et kIN 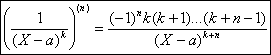
C) CritÃre
des zéros multiples.
Soit F une fraction du type F(X)=(X-a)nG(X) , le scalaire a nétant ni pôle ni zéro de G.
La formule de Leibniz appliquée au produit précédent donne lexpression de la
dérivée dordre q quelconque de F : ![]()
a étant racine dordre n de (X-a)n, il est
clair que les dérivées successives de cette puissance vont sannuler en a jusquà lordre n-1. On en déduit immédiatement, puisque
a nest pas pôle
de G, que les dérivées successives de
F vont sannuler en a jusquà lordre n-1. Quand à celle dordre n, elle prendra la valeur F(n)(a)=n!G(a) , donc sera non nulle.
On retrouve donc une caractérisation analogue à celle des racines
multiples des polynômes :
a
est zéro dordre n de la fraction F kI F(k)(a)=0 et F(n)(a) ¹ Formule
de Taylor avec reste.
Soit F une fraction rationnelle
nadmettant pas a pour pôle. Pour
tout entier n, la différence D(X)=![]() est une fraction rationnelle dont toutes les dérivées
successives jusquà lordre n
sannulent au point a. DaprÃs
ce qui précÃde, a est donc zéro
dordre au moins n+1 de F.
est une fraction rationnelle dont toutes les dérivées
successives jusquà lordre n
sannulent au point a. DaprÃs
ce qui précÃde, a est donc zéro
dordre au moins n+1 de F.
Il existe donc une fraction G
nadmettant pas a pour pôle, et telle
que D(X)=(X-a)n+1G(X).
Ainsi :![]() avec G fraction
rationnelle définie en a
avec G fraction
rationnelle définie en a
En particulier pour ![]() et pour a=0 on obtient le développement
classique :
et pour a=0 on obtient le développement
classique :
![]()
3) DECOMPOSITION EN ELEMENTS SIMPLES.
Lobjet de ce paragraphe est létude dune technique permettant décrire une
fraction rationnelle F de dénominateur
scindé comme une somme dun polynôme et de fractions élémentaires du type ![]() dans lesquel a
désigne un pôle de F, n un entier non nul inférieur ou égal
à lordre du pôle a dans F, et a un élément du corps K.
dans lesquel a
désigne un pôle de F, n un entier non nul inférieur ou égal
à lordre du pôle a dans F, et a un élément du corps K.
Cette décomposition en éléments dits simples facilitera en particulier le
calcul des dérivées successives de F
, le calcul dintégrales et de sommes relatives à la fonction
rationnelle f associée à F lorsque K est égal au corps des réels ou celui
des complexes.
La premiÃre étape de la méthode repose sur une simple division
Euclidienne.
A) Partie
entiÃre. ThéorÃme : Toute fraction rationnelle se décompose de
maniÃre unique comme somme dun polynôme avec une fraction dont le degré
du numérateur est strictement inférieur à celui du dénominateur.
_ Pour lexistence de lécriture, considérons ![]() et effectuons la
division Euclidienne de A par B. Cela se traduit par : A=B.Q+R
avec Q, R polynômes et R nul ou
de degré strictement inférieur à celui de B.
et effectuons la
division Euclidienne de A par B. Cela se traduit par : A=B.Q+R
avec Q, R polynômes et R nul ou
de degré strictement inférieur à celui de B.
En divisant par B on obtient bien un
schéma conforme à nos exigences, soit : ![]() avec degré(R) < degré(B).
avec degré(R) < degré(B).
_ Pour lunicité, supposons deux écritures de F du type précédent, soit ![]()
On en déduit légalité polynômiale : bb (E-E1)=a b ab .
Si le second membre nest pas nul, il sera de degré strictement inférieur
à la somme des degrés de b et b
daprÃs les contraintes imposés aux numérateurs a et a .
Or le premier membre est multiple de bb donc, sil
nest pas nul, est de degré supérieur ou égal à la mÃme somme des
degrés de b et b .
La seule possibilité conciliant les deux remarques est la nullité des deux
membres de légalité. On en déduit E=E1 , par intégrité de K[X] et par suite : ![]() .
.
Le polynôme E apparaissant dans la
décomposition est appelé partie
entiÃre de la fraction F.
Elle est bien sÃr nulle si F
admet un représentant dont le degré du numérateur est déjà strictement
inférieur à celui du dénominateur.
Dans ce qui suit nous ne nous occuperons que de fractions de ce type, obtenues
aprÃs division Euclidienne éventuelle.
B) Elements simples
relatifs aux pôles.
Nous supposons ici la fraction F
définie par un représentant de dénominateur scindé, cest à dire du type
![]() , avec de plus :
degré(A)< r1+
.+rn
, avec de plus :
degré(A)< r1+
.+rn
_ Envisageons dabord le cas dun pôle unique a1.
En appliquant la formule de Taylor en ce point à lordre r1-1 au numérateur A(X)
de degré strictement inférieur à r1
on obtient la relation : ![]()
En divisant par ![]() , il apparait la décomposition :
, il apparait la décomposition : ![]()
_ Nous allons généraliser ce processus par récurrence sur le nombre de pôles n.
Supposons que pour toute fraction du type décrit ci dessus on puisse
toujours trouver une décomposition du type 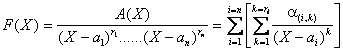 avec a(i,k) élément de K pour tout couple dindices (i,k).
avec a(i,k) élément de K pour tout couple dindices (i,k).
Examinons alors une fraction du mÃme type mais avec un pôle de plus noté a, dordre r, soit :
![]() avec
avec ![]()
a nétant pas pôle de G, on peut décomposer G en utilisant la formule de Taylor avec
reste à lordre r-1 en ce
point, ce qui donne : ![]()
avec H fraction rationnelle dont a nest pas pôle. On en déduit
lécriture de F(X) suivante :
![]() .
.
Il est clair que les pôles de H ne
sont autres que ceux de F(X) avec les mÃmes ordres de
multiplicité excepté bien sÃr le pôle a
, éliminé par intervention de la formule de Taylor ci dessus.
Pour chacun des ai avec iI on a
bien en effet :![]() avec Mi
fraction rationnelle dont ai
nest pas pôle, et H est définie en
tout x de K-.
avec Mi
fraction rationnelle dont ai
nest pas pôle, et H est définie en
tout x de K-.
De plus, en effectuant la différence ![]() , en réduisant au
mÃme dénominateur puis en simplifiant par (X-a)r, on voit
bien que le nouveau numérateur B(X) est de degré strictement inférieur
à r1+
.+rn.
, en réduisant au
mÃme dénominateur puis en simplifiant par (X-a)r, on voit
bien que le nouveau numérateur B(X) est de degré strictement inférieur
à r1+
.+rn.
Par hypothÃse on peut alors décomposer H suivant le type décrit plus haut, cest à dire :
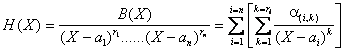
Doà une décomposition du mÃme type pour F : 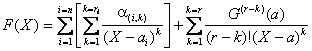
La possibilité de décomposition sétendra donc bien de proche en proche
à un nombre quelconque de pôles.
Unicité
de la décomposition, parties polaires.
On appelle partie polaire de F relative à un pôle ai de cette fraction dans une
décomposition en éléments simples de F
du type décrit ci dessus, la quantité ![]() .
.
Cette quantité ne dépend aucunement de la façon dobtenir la dite
décomposition. En effet remarquons que en multipliant F(X) par ![]() on obtient une égalité
du type :
on obtient une égalité
du type :
![]() ; ai
nétant pas pôle de Hi
; ai
nétant pas pôle de Hi
On en déduit daprÃs les rÃgles de dérivation, que : k I ![]()
La partie polaire de F relative au pôle Fi sexprime donc de maniÃre unique sous la
forme :
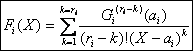 avec
avec ![]()
SynthÃse
. Nous avons donc établi le
théorÃme suivant :
Toute fraction rationnelle de dénominateur scindé se décompose de maniÃre unique comme somme de sa partie entiÃre et des parties polaires relatives à chacun de ses pôles.
Cas
particulier des pôles simples.
Si a est pôle dordre 1 de la
fraction ![]() , la partie polaire relative à a se résume alors à un seul terme du type
, la partie polaire relative à a se résume alors à un seul terme du type ![]() avec, conformément
à létude précédente, a défini par la formule
avec, conformément
à létude précédente, a défini par la formule ![]() .Ce coefficient appelé aussi résidu de la fraction F
au pôle a
.Ce coefficient appelé aussi résidu de la fraction F
au pôle a
peut se déterminer autrement si la factorisation du dénominateur D(X)
est délicate. Il suffit de remarquer que si D(X)=(X-a)B(X),
on obtient par dérivation : D(X)=B(X)+(X-a)B(X).
Ainsi
B(a)
nest autre que la valeur de la dérivée du dénominateur D de F en a : ![]()
C) Fractions
à coefficients réels.
Dans le cas oà le corps de base est celui des complexes, on sait que
tout polynôme est scindé et la décomposition en éléments simples sera toujours
possible. Si on considÃre une fraction F à coefficients purement réels, on pourra donc commencer
par la décomposer en éléments simples dans C(X). Examinons les éléments de cette décomposition.
_ La partie entiÃre, quotient dune division Euclidienne mettant en jeu
des polynômes à coefficients réels, sera donc aussi à coefficients réels.
_ Les parties polaires relatives aux pôles réels de F ne font apparaitre également que des coefficients réels. En effet
leur mode de calcul fait principalement intervenir des valeurs de dérivées
successives de fractions à coefficients réels en des nombres réels.
_ Reste le cas des éléments simples relatifs aux pôles complexes.
On rappelle que si a est
racine dordre n dun polynôme B à coefficients réels, la conjuguée
de a est
aussi racine de B et avec le
mÃme ordre de multiplicité.
Si a est pôle dordre n de F
à coefficients réels, ![]() sera donc aussi pôle
dordre n de F.
sera donc aussi pôle
dordre n de F.
Ici encore le mode de calcul des parties polaires montre que les numérateurs
des éléments simples de mÃme puissance relatifs à a et ![]() sont conjugués deux
à deux.
sont conjugués deux
à deux.
Si on réunit ainsi deux à deux ces éléments associés on obtient des
sommes du type :
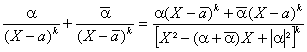 =
= ![]() avec P à coefficients réels (vu par
exemple le développement des puissances suivant la formule du binôme), et T(X)=X²-pX+q trinôme du second degré à coefficients réels de
discriminant strictement négatif.
avec P à coefficients réels (vu par
exemple le développement des puissances suivant la formule du binôme), et T(X)=X²-pX+q trinôme du second degré à coefficients réels de
discriminant strictement négatif.
Ces éléments sont bien maintenant à coefficients réels mais ils ne sont
pas simples car le degré du numérateur P
peut Ãtre élevé.
(Il est au plus égal à k et
égal à k si le coefficient a nest pas
imaginaire pur).
Effectuons alors la division Euclidienne de P
par T. Il vient ![]()
et par suite : ![]()
La deuxiÃme fraction a un dénominateur de degré au plus 1, on peut le
considérer comme simple au sens que son intégration par exemple peut
Ãtre obtenu selon un schéma classique que nous aborderons ultérieurement
dans le cours dAnalyse.
La premiÃre admet un numérateur P1
dont le degré a notablement régressé par rapport à celui de P. On peut alors poursuivre le processus
sur cette fraction en divisant maintenant P1
par T .
En répétant ce principe, vu la décroissance des degrés des numérateurs, on
obtiendra au bout dun nombre fini détapes une somme de termes du type ![]() avec i indice appartenant
avec i indice appartenant
à la plage . Et ceci
pour tout k inférieur ou égal
à lordre du pôle a.
La somme des parties polaires relatives à a et ![]() dordres r sera donc du type
dordres r sera donc du type ![]()
Fractions Rationnelles. Exercices.
Décomposer en éléments simples
dans R(X) les fractions
suivantes :
![]()
Pour n entier non nul décomposer en éléments simples dans R(X) la fraction ![]()
Décomposer en éléments simples
dans C(X) puis dans R(X) les fractions suivantes :
![]()
Décomposer en éléments simples dans
C(X) les fractions
suivantes :
![]()
Pour n entier non nul décomposer en éléments simples dans C(X):
![]()
On pose P(X)=4X3+4(1-i)X²-(1+4i)X
1.
Montrer que P(X) admet une racine
multiple, puis décomposer la fraction ![]() en éléments simples
dans C(X).
en éléments simples
dans C(X).
Décomposer en éléments simples
dans R(X) la fraction ![]() sachant que le
paramÃtre a est réel et que le
dénominateur admet une racine multiple.
sachant que le
paramÃtre a est réel et que le
dénominateur admet une racine multiple.
On considÃre la fraction
de R(X) définie par ![]()
Décomposer F(X) en une somme déléments du type ![]() avec k exposant entier et Ak , Bk réels.
avec k exposant entier et Ak , Bk réels.
(On pourra procéder par divisions Euclidiennes successives)
On considÃre pour n entier P(X)=X(X-1)(X-2)
..(X-n).
Décomposer sur R(X) les fractions ![]()
Décomposer en éléments simples
sur R(X) la fraction F(X)=![]() puis en déduire le calcul des expressions suivantes :
puis en déduire le calcul des expressions suivantes :
a) ![]()
b) F(n)(X) pour n entier quelconque.
c) ![]() pour n entier quelconque.
pour n entier quelconque.
Décomposer dans R(X) la fraction F(X)=![]() puis en déduire les expressions de :
puis en déduire les expressions de :
a) ![]() b) F(n)(X) pour n entier . c)
b) F(n)(X) pour n entier . c) ![]() pour n entier non nul.
pour n entier non nul.
On considÃre la
fraction : ![]()
a) Décomposer F(X) en éléments simples dans R(X)
b) En déduire une expression simplifiée de ![]() pour n entier non nul, puis la limite de la somme
précédente lorsque n tend vers + ¥
pour n entier non nul, puis la limite de la somme
précédente lorsque n tend vers + ¥
On considÃre la
fraction : ![]()
a) Décomposer F(X) en éléments simples sur R(X)
b) En déduire la valeur de ![]()
c) Montrer que pour tout entier n ³ ![]()
Déterminer les intégrales
suivantes :
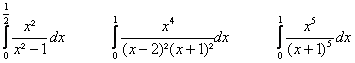
Déterminer les dérivées
successives des fractions suivantes :
![]() (q I p
(q I p
Nombres de Fibonacci. On considÃre la fraction f(X)=![]()
a) Montrer que pour tout entier n ³2 on a la relation
suivante :
(1-X-X²)f(n)(X)-n(2X+1)f(n-1)(X)-n(n-1)f(n-2)(X)=0 .
(On pourra partir de légalité (1-X-X²)f(X)=1
puis appliquer Leibniz.)
b) En utilisant la décomposition de f(X) en éléments simples dans C(X), déterminer directement lexpression
de la dérivée successive dordre n de
f.
c) Montrer à laide de a), que pour tout n entier le réel Fn=![]() nest autre que le nombre de Fibonacci dordre n définie par le processus de récurrence :
nest autre que le nombre de Fibonacci dordre n définie par le processus de récurrence :
F0=1 ; F1=1 ;
k IN Fk+2=Fk+1+Fk.
d) Trouver alors à laide de b) une expression directe de Fn en fonction de lentier n.
On considÃre n complexes distincts X1,X2,
,Xn et le polynôme P(X)=(X-X1).
.(X-Xn)
a) Décomposer en éléments simples dans C(X)
la fraction 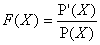 .
.
b) En déduire lexpression simplifiée pour X
IC- des sommes suivantes :
![]()
On considÃre n complexes distincts a1, a2,
.,an
et P un polynôme à coefficients dans C, de degré strictement inférieur à n, nayant pour racine aucun des n complexes ci dessus.
a) Décomposer en éléments simples dans C(X)
la fraction ![]()
b) En déduire alors la valeur pour qI de la somme :
(lindice j dans chacun des
dénominateurs parcourant - )
P(X) désigne un polynôme à
coefficients complexes de degré strictement inférieur à lentier n.
a) Décomposer dans C(X) la fraction F(X)=![]() . On notera a1,
.,an les pôles de F(X)
. On notera a1,
.,an les pôles de F(X)
b) Montrer que F(X)=![]() .
.
c) En appliquant ce qui précÃde à P(X)=X, trouver une expression
condensée de la somme : ![]() pour x réel donné.
pour x réel donné.
On considÃre la fraction ![]()
a) Montrer que lon peut choisir les réels a,
b, c, de façon que la suite définie par yn=![]() coÃncide
exactement avec la suite définie par le procédé de récurrence :
coÃncide
exactement avec la suite définie par le procédé de récurrence :
x0=1 ; x1=1 ; x2=1 et kIN xk+xk+1+xk+2+xk+3=0.
(On utilisera la formule de Leibniz pour dériver le produit f(X)(1+X+X²+X3) )
b) Décomposer f(X) en éléments simples sur C(X)
pour les valeurs de a,b,c
précédentes, puis en déduire lexpression directe de xn en fonction de n.
SOLUTIONS.
a)
Noublions pas la partie entiÃre, obtenue par division Euclidienne :
X3=(X²-3X+2)(X+3)+7X-6 , donc ![]()
![]()
Ainsi : ![]()
b) La partie entiÃre est nulle.
La partie polaire relative à 2 est ![]()
La partie polaire relative au pôle double 1 sera ![]()
AprÃs calculs : 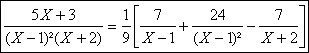
c) La partie entiÃre est 1 puisque X3+7=(X3-8)+15.
La fraction possÃde trois pôles simples sur C qui sont le produit par 2 des racines cubiques de lunité,
soit 2, 2j et 2j² avec ![]()
![]()
On peut éviter la factorisation du dénominateur en calculant les résidus
à laide de la dérivée 3X²
de ce mÃme dénominateur. En chacun de ces pôles z, la partie polaire est égale à ![]() Ainsi on obtient dans C(X) puis R(X) :
Ainsi on obtient dans C(X) puis R(X) :
![]()
![]()
Pour
n entier non nul et X complexe distinct de 1 et 1 on sait
que :
![]() .
.
On en déduit la partie entiÃre,
puis la décomposition évidente : ![]()
a)
La fraction a 4 pôles simples complexes qui sont les racines quatriÃmes
de 1 et sont donnés par les formules trigonométriques ![]() avec k I.
avec k I.
La partie entiÃre étant nulle, on a donc : ![]()
AprÃs calculs et simplifications on obtient la décomposition dans C(X) suivante :
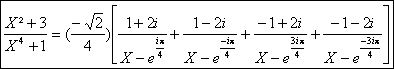 , puis la
décomposition dans R(X), en regroupant deux à
deux les parties polaires relatives à un pôle et son conjugué :
, puis la
décomposition dans R(X), en regroupant deux à
deux les parties polaires relatives à un pôle et son conjugué :
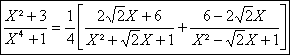
b) La fraction a 3 pôles simples dans C
qui sont les racines cubiques de lunité et un pôle double, soit 1.
Pour celui ci la partie polaire est ![]()
On trouve facilement grace à : ![]()
les valeurs ![]()
Pour chacune des racines cubiques z
de 1, la partie polaire est ![]()
et D(z)=2(z+1)(z3-1)+(z+1)²(3z²) dérivée du dénominateur de la fraction
donnée.
AprÃs calculs et simplifications on obtient la décomposition dans C(X) suivante :
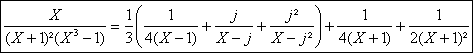 avec
avec ![]()
En regroupant les termes en j et j² on obtient la décomposition dans
R(X) :
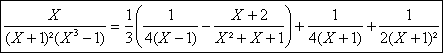
c) Ecrivons dabord la fraction sous forme irréductible : ![]()
La partie entiÃre est égale à 1 et la fraction admet deux pôles
doubles dans C soit i et i
Les coefficients étant tous réels, la décomposition dans C(X) sera : ![]()
Avec b=G(-i) , a=G(-i) et G(X)=-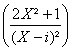 .
.
AprÃs calculs on obtient :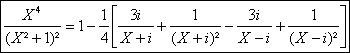
On peut obtenir directement la décomposition dans R[X] à partir de la division Euclidienne : 2X²+1=(X²+1)2-1 doà lon tire en divisant par (X²+1)² la relation :
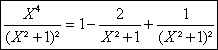
a)
![]()
La fraction ci dessus admet quatre pôles simples complexes qui sont les racines
sixiÃmes de lunité distinctes de 1 et 1, soient j, -j, j²,-j² avec ![]()
Les coefficients étant tous réels et vu la parité de la fraction on aura donc
une décomposition dans C(X) du type suivant :
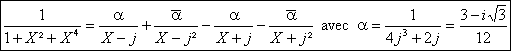
Dans R(X) on aurait aprÃs
regroupement : ![]()
b) (X+1)5=X5 ![]() . Les pôles sont donc obtenus à partir des racines
cinquiÃmes de lunité
. Les pôles sont donc obtenus à partir des racines
cinquiÃmes de lunité ![]() avec kI en résolvant
avec kI en résolvant ![]()
On trouve 4 solutions 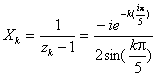 avec kI
avec kI
La partie polaire relative au pôle simple Xk
sera 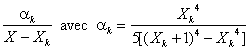
En simplifiant : 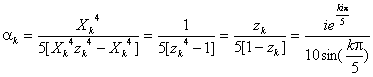
Attention, la partie entiÃre nest pas nulle mais égale à ![]() car le terme dominant
de (X+1)5-X5 est 5X4. Ainsi :
car le terme dominant
de (X+1)5-X5 est 5X4. Ainsi : 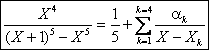
c) 0 est pôle simple , j et j² sont pôles doubles. La partie
entiÃre est nulle. Doà la décomposition dans C(X) : ![]()
![]() ;
; ![]()
AprÃs calculs et simplifications on trouve ![]()
Ainsi : 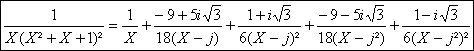
La décomposition dans R(X) donnerait :![]()
a)
Les pôles sont les racines niÃmes de lunité : : ![]() avec kI.
avec kI.
Sagissant de pôles simples et la partie entiÃre étant nulle, la
décomposition est évidente :
![]() .
. ![]()
b) Les pôles sont ceux de la fraction précédente, presque tous simples, sauf 1
dordre de multiplicité 2 puisque ![]()
La partie polaire relative à 1 sera donc 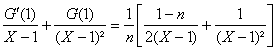
Le résidu au pôle simple zk
pour k ¹0 sera 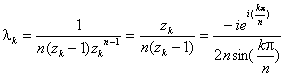
Ainsi 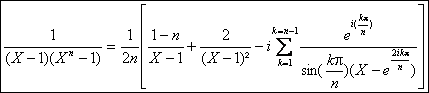
c) Il y a 2n+1 pôles simples définis
par zk=![]() avec kI.
avec kI.
Le résidu en chacun de ces pôles est donné par ak=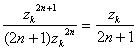 .
.
La partie entiÃre est égale à 1. Ainsi : 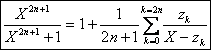
Si
P(X) admet une racine multiple, celle ci doit Ãtre nécessairement racine
commune à P(X) et sa dérivée formelle P(X). Suivant le schéma classique
de recherche des zéros communs nous effectuons alors la division Euclidienne de
P(X) par P(X) soit :
![]() La seule racine multiple possible est donc
La seule racine multiple possible est donc ![]() . On vérifie facilement que cette valeur est effectivement
racine double : P(X)=4(X-
. On vérifie facilement que cette valeur est effectivement
racine double : P(X)=4(X-![]() )²(X+1)
)²(X+1)
On en déduit P(X)=8(X-![]() )(X+1)+4(X-
)(X+1)+4(X-![]() )² , puis :
)² , puis :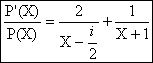
Si
x est racine multiple du dénominateur
D(X)=aX3-3X+a+1, x
doit Ãtre nécessairement racine de D(X)=3aX²-3, donc vérifier ax²=1.
En faisant intervenir cette relation dans légalité D(x)=0 on en déduit alors 2x=a+1. La seule valeur possible est donc ![]()
qui sera effectivement racine double si ![]() ou encore si a3+2a²+a-4=0.
ou encore si a3+2a²+a-4=0.
Vu la factorisation évidente en (a-1)(a²+3a+4), il apparait que 1 est la seule valeur réelle possible pour a. On a dans ce cas D(X)=(X-1)²(X+2).
La décomposition de la fraction donnée, de pôle double 1 et pôle simple 2
sobtient facilement : 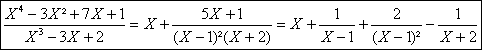
Une
premiÃre division de X6 par X²+X+1 donneX6=(X²+X+1)(X4-X3+X-1)+1
et conduit à lapparition dun premier élément simple : ![]() . Continuons en divisant X4-X3+X-1 par
X²+X+1. On obtient : X4-X3+X-1=(X²+X+1)(X²-2X+1)+2X-2
et par suite :
. Continuons en divisant X4-X3+X-1 par
X²+X+1. On obtient : X4-X3+X-1=(X²+X+1)(X²-2X+1)+2X-2
et par suite :
![]()
Enfin, de X²-2X+1=(X²+X+1)(1)-3X on déduit la forme ultime
demandée :
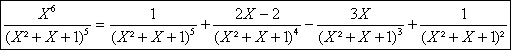
a)
Le résidu ak au pôle simple entier k de est égal au quotient du numérateur constant 1 par le produit k(k-1)(k-2)
(2)(1)(-1)(-2)
(-(n-k))=(-1)n-kk!(n-k)!
On peut donc écrire en utilisant les coefficients binômiaux : ak=(-1)n-k![]()
On vérifie que cette expression est également valable aux pôles extrÃmes
0 et n.
Ainsi : 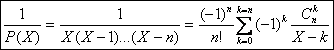
b) Le résidu au pôle simple entier k
de ![]() est égal à
est égal à ![]() . La partie entiÃre est nulle, doà la
décomposition évidente :
. La partie entiÃre est nulle, doà la
décomposition évidente : ![]()
c) En dérivant formellement légalité ci-dessus on obtient :
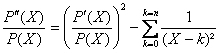 .
.
En évaluant le carré de ![]() on obtient :
on obtient :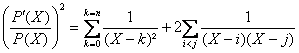
Or 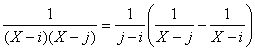 . On en déduit donc la décomposition :
. On en déduit donc la décomposition :
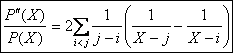 , la somme étant
étendue à tous les couples (i, j) dentiers compris entre 0 et n tels que i <j.
, la somme étant
étendue à tous les couples (i, j) dentiers compris entre 0 et n tels que i <j.
La décomposition de F est évidente : ![]()
Applications :
a) 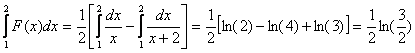
b) F(n)(X)=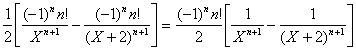
c) ![]()
Décomposition élémentaire : ![]()
a) ![]()
b) F(n)(X)=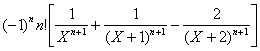
c) ![]()
a) La partie entiÃre est
nulle et les deux pôles sont dordre 2. On peut donc écrire la
décomposition : ![]()
avec ![]() . AprÃs calculs et simplifications il vient :
. AprÃs calculs et simplifications il vient : ![]()
b) ![]()
![]()
a) La partie entiÃre
sobtient facilement par division.
Les parties polaires en 0, simple et en 1, pôle double ne posent pas non plus
de problÃmes
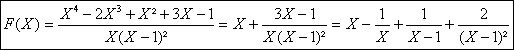
b) 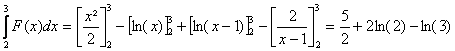
c) ![]()
a) ![]() DoÃ
Doà 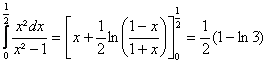
b) 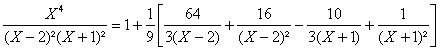
Doà : 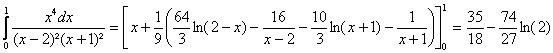
c) DaprÃs la formule du binôme :
(x)5=[(x+1)-1]5=(x+1)5-5(x+1)4+10(x+1)3-10(x+1)²+5(x+1)-1. On en déduit aussitôt :
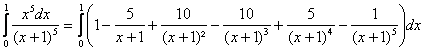 , soit en
développant :
, soit en
développant :
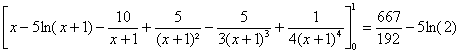
a) ![]() , Doà pour
tout entier n³2 :
, Doà pour
tout entier n³2 : 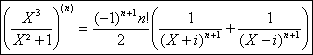
b) 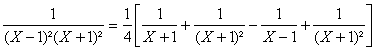
La dérivée dordre n est donc donnée
par la formule suivante :
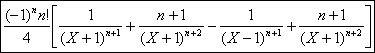
c) La fraction admet deux pôles simples complexes conjugués, eiq et e-iq.
La décomposition est élémentaire : ![]()
Ainsi la dérivée dordre n sexprime
par : 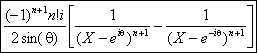
a) Les dérivées successives de 1-X-X
² sannulent à partir de lordre 3.
La formule de Leibniz appliquée au produit (1-X-X)f(X) donne donc une
expression de la dérivée dordre n
réduite pour n ³2 à :
![]()
Soit aprÃs simplifications : (1-X-X²)f(n)(X)+n(-1-2X)f(n-1)(X)-n(n-1)f(n-2)(X)
Or par définition de la fraction f,
le produit étudié est constant égal à 1. Doà la relation :
n ³ (1-X-X²)f(n)(X)-n(2X+1)f(n-1)(X)-n(n-1)f(n-2)(X)=0 .
b) La fraction f admet deux pôles
simples réels définis par a=![]() et b=
et b=![]() .
.
La décomposition est immédiate : ![]()
On en déduit directement lexpression de la dérivée dordre n pour n entier quelconque :
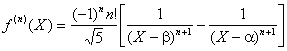
c) Pour X=0, la relation établie en
a) se simplifie en : f(n)(0)-nf(n-1)(0)-n(n-1)f(n-2)(0)=0
On en tire immédiatement : ![]() , cest à dire avec les notations de lénoncé : n ³2 : Fn=Fn-1+Fn-2. Il reste à déterminer, par un calcul
direct des valeurs de f et de sa
dérivée en 0, les conditions initiales, soit : F0=f(0)=1 et F1=f (0)=1.
, cest à dire avec les notations de lénoncé : n ³2 : Fn=Fn-1+Fn-2. Il reste à déterminer, par un calcul
direct des valeurs de f et de sa
dérivée en 0, les conditions initiales, soit : F0=f(0)=1 et F1=f (0)=1.
d) La formule obtenue en b) donne pour X=0
lexpression directe de Fn
en fonction de lentier n,
soit : 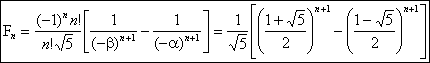
a) La partie entiÃre de ![]() est nulle et le résidu
en chacun des pôles simples Xk
est nulle et le résidu
en chacun des pôles simples Xk
est donné par la relation classique ak=![]()
On a donc la décomposition élémentaire : ![]() =
=![]()
b) Pour XIC-
on déduit aussitôt de la formule ci dessus : ![]()
De ![]() on tire ensuite :
on tire ensuite :
![]()
![]()
Enfin, en dérivant formellement la décomposition de F(X) on arrive à :
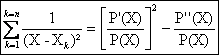
a) Le schéma est classique,
partie entiÃre nulle et n
pôles simples ak en lequel
la partie polaire se résume à 
b) Appliquons le résultat précédent à P(X)=Xq avec qI. On peut alors écrire :
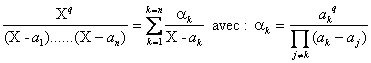
Multiplions alors légalité précédente par X et décomposons ![]()
On en déduit : ![]()
Or puisque q<n, la partie entiÃre de la
fraction ci dessus est nulle si q<n-1 et vaut 1 si q égale n-1. Doà lexpression de la somme des ak, et ceci vu lunicité de la
décomposition dune fraction donnée en éléments simples. 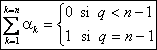
a) La partie entiÃre est
nulle puisque le degré de P est strictement inférieur à n.
La partie polaire relative au pôle simple ![]() est égale à
est égale à ![]()
avec : ![]() . On en déduit :
. On en déduit : ![]()
En particulier pour X=0 on obtient : P(0)=![]() .
.
b) Décomposons alors : ![]() . On en déduit la relation suivante :
. On en déduit la relation suivante :
![]()
c) Appliquons légalité précédente pour P(X)=X en X=![]() , avec x choisi tel
que Xn¹1.
, avec x choisi tel
que Xn¹1.
Pour tout k de : 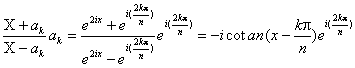
Ainsi : ![]()
En égalant les parties réelles on en déduit aprÃs simplifications :
![]()
Il sagit dune généralisation de
lexercice 16.
a) Dérivons formellement à lordre n
les deux membres de légalité de définition de f, ![]() . Pour n ³3, et daprÃs Leibniz, on
est conduit à :
. Pour n ³3, et daprÃs Leibniz, on
est conduit à :
![]() . Pour X=0 cette
relation se résume à :
. Pour X=0 cette
relation se résume à :
![]()
Ainsi, les termes ![]() satisfont bien
à la relation de récurrence :
satisfont bien
à la relation de récurrence :
n³ yn+yn-1+yn-2+yn-3=0. Pour
obtenir des termes initiaux y0,
y1, y2 égaux à 1, il suffit dajuster les
coefficients a, b, c de façon que f(0)=1 ;
f (0)=1 ; ![]() .
.
On trouve facilement, de proche en proche : c=1 ; b=2 ; a=3.
b) La décomposition de f est
évidente : ![]()
On en déduit :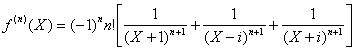
Et donc ![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2854
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved