Masurarea impedantelor

Masurarea impedantelor

Impedanta este o marime ce caracterizeaza functionarea elementelor de circuit in curent alternativ. Ea se defineste cu ajutorul legii lui Ohm aplicata in curent alternativ:

Z=U/I [Ω] (3.47)

Deoarece rezistenta in curent continuu si impedanta in curent alternativ au aceiasi relatie de definitie, metodele utilizate pentru masurarea rezistentelor in curent continuu se pot adopta si la masurarea impedantelor in curent alternativ, cu urmatoarele observatii:

circuitele de masurare vor fi alimentate3 in curent alternativ;

aparatele de masura folosite trebuie sa functioneze la frecventa f a sursei de alimentare;

elementele de circuit, fiind alimentate in curent alternativ, se vor comporta ca impedante.

1. Masurarea impedantei prin metoda substitutiei

Cu comutatorul K pe pozitia 1 se masoara curentul prin circuit I=U/Z_x. Se trece K pe pozitia 2 si se regleaza R₀ pana cand curentul prin acest circuit este egal cu curentul prin circuitul anterior, astfel incat:

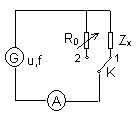
si deci Z_x=R₀ (3.48)

G - sursa de tensiune alternativa de tensiune U (valoare efectiva) si frecventa f;

R₀ - rezistenta etalon variabila;

K - comutator cu doua pozitii;

A - ampermetru de c.a.

Fig.3.17. Masurarea impedantei prin metoda substitutiei

Dupa cum se observa, aceasta metoda permite numai masurarea globala a impedantelor, nu si a componentelor R, L, C.

2. Masurarea inductantei prin metoda ampermetrului si voltmetrului

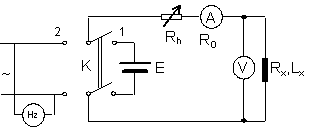Masurarea inductantelor proprii ale bobinelor folosind metoda voltampermetrica se bazeaza pe comportarea diferita a bobinelor in c.c. si in c.a. Intrucat bobinele au de obicei impedante mult mai mici decat rezistenta voltmetrului, se foloseste varianta aval.

Fig.3.18. Masurarea inductantelor proprii prin metoda voltampermetrica

Se inchide comutatorul K pe pozitia 1 si montajul se alimenteaza in c.c. Se citesc indicatiile ampermetrului (I) si voltmetrului (U) si apoi se calculeaza rezistenta ohmica a bobinei R_x:

R_x=U/I (3.49)

Se trece K pe pozitia 2 si montajul se alimenteaza in c.a. Se citesc din nou indicatiile ampermetrului (I) si voltmetrului (U) si se calculeaza impedanta bobinei:

Z_x=U/I (3.50)

Cunoscand R_x si Z_x si cunoscand sau masurand frecventa se poate deduce valoarea inductantei:

(3.51)

de unde    (3.52)

3. Punti de curent alternativ

Sunt utilizate la masurarea impedantelor avand aceiasi schema de principiu si acelasi mod de functionare ca si puntile de c.c. Puntea de c.a este alimentata de la o sursa de c.a. de frecventa f, elementele din bratele sale se comporta ca impedante, iar indicatorul de nul trebuie sa functioneze la frecventa f a sursei.

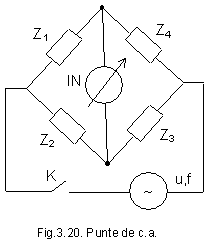Ca si la puntile de c.c., cand prin indicatorul de nul curentul este zero, intre cele patru brate ale puntii exista o relatie bine determinata, cunoscuta sub denumirea de conditia de echilibru, si care este similara cu cea de la puntile de c.c. (produsul a doua brate opuse este egal cu produsul celorlalte doua brate opuse, sau raportul a doua brate alaturate este egal cu raportul celorlalte doua brate alaturate).

Z₁Z₃ = Z₂Z₄ sau Z₁/Z₂ = Z₄/Z₃ (3.56)

Fiecare impedanta poate fi exprimata prin modulul sau |Z| si prin defazajul φ pe care il introduce:

Z=|Z|e^jφ (3.57)

Ca urmare, conditia de echilibru se poate scrie sub forma:

(3.58)

ceea ce este echivalent cu doua relatii: una referitoare la module si cealalta la faze:

(3.59)

Cea de-a doua relatie arata ca puntile de c.a. nu pot avea orice configuratie. Astfel, daca in doua brate opuse ale unei punti de c.a. sunt numai rezistente in celelalte doua brate trebuie sa fie reactante de semne contrare (inductanta-capacitate). Daca in doua brate alaturate sunt numai rezistente, atunci in celelalte doua brate alaturate trebuie sa fie reactante de acelasi fel (inductanta-inductanta sau capacitate-capacitate).

Ca si la puntile de c.c., daca se cunosc elementele din trei brate, se pot deduce elementele din al patrulea. Pentru calcule, se utilizeaza de obicei, exprimarea impedantelor sub forma numerelor complexe:

Z=R+jX (3.60)

si deci conditia de echilibru devine:

(R₁+jX₁)( R₃+jX₃) = (R₂+jX₂)(R₄+jX₄) (3.61)

Desfacand parantezele si separand partea reala de partea imaginara se obtin doua relatii care impreuna exprima conditia de echilibru:

(3.62)

Pentru satisfacerea celor doua relatii de echilibru, la puntile de c.a. sunt necesare doua elemente de reglej. Acestea pot fi rezistente sau condensatoare variabile, deoarece bobinele variabile de inductanta cunoscuta sunt mai greu de realizat practic.

Exista o mare diversitate de punti de c.a., ele denumindu-se de obicei, dupa numele savantilor ce le-au produs.