Electromecanica

C. L. C. S.

 

Decodificator BCD exces 3/ 7 segmente (logica combinationala).Se va studia cazul in care elementele tubului de afisare cu 7 segmente sunt aprinse initial cat si cazul in care elementele tubului sunt stinse initial. Proiectarea se va referi la o singura decada. Proiectul va cuprinde urmatoarele puncte:

a)   Sa se exprime functiile logice asociate circuitului combinational cu FCD (forma canonica disjunctiva), FCC (forma canonica conjunctiva), tabel de adevar si diagrame Karnaugh.

b)   Sa se obtina formele minime disjunctive si conjunctive pentru functiile logice asociate decodificatorului BCD exces 3/ 7 segmente (utilizand combinatiile indiferente) prin metoda diagramelor Karnaugh; se vor obtine, de asemenea, formele minime disjunctive pentru doua dintre functiile logice de iesire 3, 4 si prin metoda Quine-McCluskey.

c)   Sa se implementeze fiecare functie logica, independent, numai cu porti logice SI-NU (portile logice sunt realizate in tehnologia TTL).

d)     Sa se implementeze ansamblul functiilor logice numai cu porti logice SI-NU (portile logice sunt realizate in tehnologia TTL).

e)   Sa se implementeze ansamblul functiilor logice in urmatoarea varianta: primele 3 functii logice de iesire cu porti logice SI-NU, realizate in tehnologia TTL, iar urmatoarele 4 cu porti logice SAU-NU, realizate in tehnologia CMOS.

f)      Sa se implementeze ansamblul functiilor logice cu MUX-uri de 8 respectiv 16 cai (circuitele sunt realizate in tehnologia TTL ).

g)     Sa se implementeze ansamblul functiilor logice cu DMUX-uri de 8 respectiv 16 cai si porti logice SI-NU in prima varianta, respectiv SI in a doua varianta (toate circuitele sunt realizate in tehnologia CMOS ).

h)     Sa se calculeze timpii de propagare "intrare-iesire", pentru toate schemele logice obtinute.

i)       Sa se calculeze puterile disipate pentru toate schemele logice obtinute.

j)       Sa se compare solutiile de implementare obtinute.

k)     Se va face analiza, prin simulare, a tuturor schemelor logice obtinute utilizandu-se pachetul de programe OrCAD.

l) Pe schemele logice obtinute se vor specifica tipul si gradul de utilizare al fiecarui circuit integrat.

Proiect

a

	g

Tabelul de adevar:

Este o modalitate eficienta si usor de realizat pentru descrierea directa a unei functii logice. Tabelul de adevar contine valorile "0" sau "1" ale variabilelor de intrare si valoarea functiei pentru fiecare combinatie posibila a variabilelor de intrare.

Pentru determinarea formelor canonice conjunctiva si disjunctiva se folosesc aceste tabele de adevar. FCD se obtine facand disjunctia tuturor termenilor pentru care functia are valoarea "1". Fiecare termen se obtine prin conjunctia variabilelor. FCC se obtine facand conjunctia tuturor termenilor pentru care functia ia valoarea "0". Fiecare termen se obtine din disjunctia negatelor variabilelor.

Formele canonice normale

O functie booleana se poate scrie in doua moduri, sau forme canonice:

- forma canonica disjunctiva -FCD;

- forma canonica conjunctiva -FCC.

O functie cu n termeni are in forma canonica m=2ⁿ termeni.

a) Formele canonice normal disjunctive

a^FCD å(3,5,6,8,9,10,11,12)=

b^FCD å(3,4,5,6,7,10,11,12)=

c^FCD å(3,4,6,7,8,9,10,11,12)=

d^FCD å(3,5,6,8,9,11,12)=

e^FCD å(3,5,9,11)=

f^FCD å(3,7,8,9,11,12)=

g^FCD å(5,6,7,8,9,11,12)=

Forma canonica normal conjunctiva

a^FCC=Q4Q7=

b^FCC=Q8Q9=

c^FCC=Q5=

d^FCC=Q4Q7Q10=

e^FCC=Q4Q6Q7Q8Q10Q12=

f^FCC=Q4Q5Q6Q10=

g^FCC=Q3Q4Q10=

Metoda diagramelor Karnaugh este o metoda grafo-analitica, foarte utila la minimizarea functiilor cu un numar relativ mic de variabile. Metoda porneste de la una din formele canonice ale functiei.

Diagrama Karnaugh se prezinta sub forma unui patrat sau dreptunghi cu 2ⁿ locatii, in cazul nostru 16 locatii. In fiecare locatie va apare un termen canonic al functiei.

Diagrama este astfel organizata, incat doua compartimente vecine pe linie sau pe coloana, sa difere printr-o aceeasi variabila, variabila care intr-o combinatie sa apara negata, si in alta adevarata. (proprietatea de adiacenta)

O functie booleana, data sub forma canonica disjunctiva, poate fi reprezentata pe diagrama Karnaugh marcand de exemplu cu 1 compartimentele corespunzatoare    termenilor canonici ai functiei.

b). Sa se obtina formele minime disjunctive si conjunctive pentru functiile logice asociate decodificatorului BCD exces 3/ 7 segmente (utilizand combinatiile indiferente) prin metoda diagramelor Karnaugh; se vor obtine, de asemenea, formele minime disjunctive pentru doua dintre functiile logice de iesire 3, 4 si prin metoda Quine-McCluskey.

Forma minima

Problema sintezei unei retele de comutare consta in gasirea acelei retele de comutare care realizeaza functia de comutare data. Exista mai multe retele care realizeaza aceeasi functie de comutare. Pentru practica intereseaza acea retea care corespunde circuitului realizabil cu un cost    cat mai mic, pentru tipul de element dat. In scopul obtinerii acestei retele se procedeaza la minimizarea functiei de comutare data. Pentru minimizarea unei functii de comutare complet definita exista doua metode:

metoda diagramelor Karnaugh;

metoda Quine McCluskey.

1. Metoda diagramelor Karnaugh:

Doua compartimente vecine pe diagrama Karnaugh reprezinta un cub unidimensional. Un grup de patru compartimente dintre care fiecare este vecin cu alte doua compartimente din acelasi grup, formeaza un subcub bidimensional. In cazul general, termenii canonici care formeaza un subcub k-dimensional, se pot inlocui cu un termen normal avand    cu k variabile mai putin decat termenii canonici.

Un subcub care nu este inclus intr-un subcub de dimensiune mai mare se numeste    implicant prim al functiei date. Formand suma booleana a tuturor implicantilor primi ai unei functii date se obtine o forma minima disjunctiva a acesteia, care in cazul general este mult mai simpla decat forma canonica disjunctiva a acestei functii. Pentru a obtine implicantii primi ai unei functii reprezentata pe diagrama Karnaugh, compartimentele marcate cu "1" trebuie astfel grupate incat sa se obtina subcuburi cu dimensiunea cea mai mare posibila.

Forma minima disjunctiva

a^FMD=

b^FMD=

c^FMD=

d^FMD=

e^FMD=

f^FMD=

g^FMD=

Forma minima conjunctiva

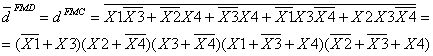
2.Metoda de minimizare Quine McCluskey:

Aceasta metoda este o metoda analitica. Se porneste tot de la una din formele canonice ale functiei de minimizat. Metoda are doua etape:

in prima se determina termenii elementari posibili (implicanti primi), folosindu-se un procedeu de comparatie;

in a doua etapa se aleg dintre implicntii primi obtinuti la finele primei etape doar aceia care acopera (includ) toti termenii canonici ai functiei date si asigura realizarea acesteia la un pret de cost minim.

Etapa 1:

- se compara echivalentii binari ai termenilor canonici in sensul descoperirii proprietatii de adiacenta (Doua combinatii binare sunt adiacente daca difera printr-o aceeasi variabila sau grup de variabile care intr-una apare adevarata si in cealalta negata. Aceasta variabila se numeste variabila redundanta.)

- in momentul cand se gasesc doi termeni adiacenti, variabila redundanta se elimina si rezulta un termen elementar.

- vor avea loc atatea cicluri de comparatii pana cand nu vor mai exista termeni elementari care sa aiba proprietatea de adiacenta.

Etapa 2:

- se aleg dintre implicantii primi obtinuti la sfarsitul primei etape doar aceia care acopera (includ) toti termenii canonici ai functiei initiale. La intersectia unei linii cu o coloana se pune un asterix (*) care va indica faptul ca implicantul prim de pe coloana include termenul canonic corespunzator.

- daca pe o linie se afla un singur asterix atunci implicantul prim corespunzator este implicant prim esential si va aparea in mod obligatoriu in forma minima a functiei. Daca acestia nu includ toti termenii canonici ai functiei, se aleg dintre ceilalti implicanti primi numarul minim care sa realizeze acest lucru.

c^FCD å

Etapa1

*P0=(combinatie indiferenta)

*P1=(combinatie indiferenta)

*P2=(combinatie indiferenta)

P3=

P4=

P6=

P7=

P8=

P9=

P10=

P11=

P12=

*P13=(combinatie indiferenta)

*P14=(combinatie indiferenta)

*P15=(combinatie indiferenta)

Rezultatele comparatiilor

Compararea termenilor elementari:

c^FMD=

Etapa 2

IP_E IP_E IP_E IP_E

Rezulta forma minima disjunctiva:

c^FMD=

d^FCD å

*P0=(combinatie indiferenta)

*P1=(combinatie indiferenta)

*P2=(combinatie indiferenta)

P3=

P5=

P6=

P8=

P9=

P11=

P12=

*P13=(combinatie indiferenta)

*P14=(combinatie indiferenta)

*P15=(combinatie indiferenta)

Rezultatul comparatiilor:

Compararea termenilor elementari:

d^FMD=

Etapa 2

IP_E IP_E IP_E IP_E IP_E

Rezulta forma minima disjunctiva:

d^FMD=

c).Sa se implementeze fiecare functie logica, independent, numai cu porti logice SI-NU (portile logice sunt realizate in tehnologia TTL).

Se pleaca de la FMD. Se neaga de doua ori (pentru a nu schimba functia), apoi se aplica teoremele lui DeMorgan

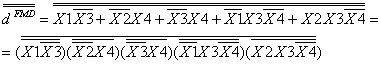
Pentru functia a schema implementata este urmatoarea:

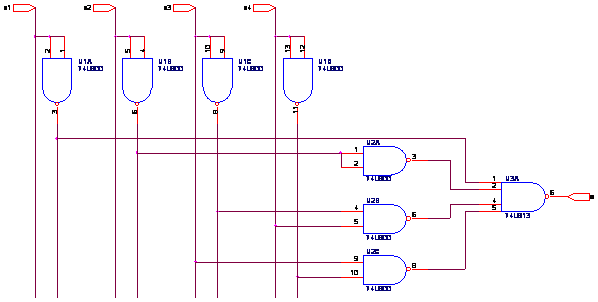
Pentru fiecare functie se procedeaza asemanator.

d).Sa se implementeze ansamblul functiilor logice numai cu porti logice SI-NU (portile logice sunt realizate in tehnologia TTL).

Tipul portilor logice folosite:

Implementarea ansamblului de functii este prezentata mai jos:

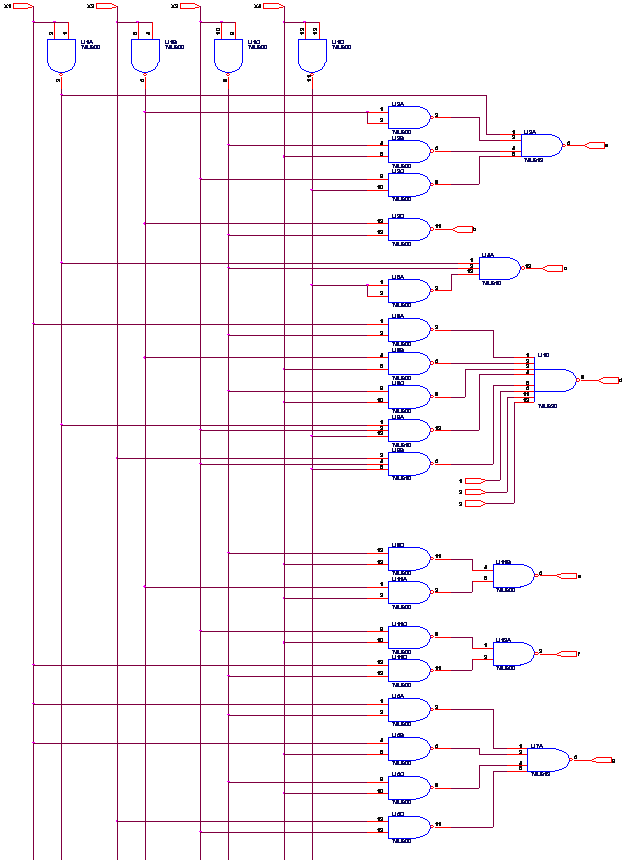
e).Sa se implementeze ansamblul functiilor logice in urmatoarea varianta: primele 3 functii logice de iesire cu porti logice SI-NU, realizate in tehnologia TTL, iar urmatoarele 4 cu porti logice SAU-NU, realizate in tehnologia CMOS.

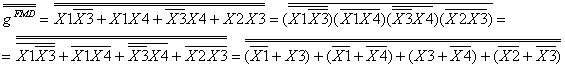
Portile folosite sunt de tipul CMOS:

si de tipul TTL:

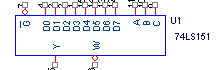
f).Sa se implementeze ansamblul functiilor logice cu MUX-uri de 8 respectiv 16 cai (circuitele sunt realizate in tehnologia TTL ).

Pentru MUX-uri de 8 cai alegem 74LS151 sau 74LS152

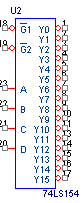
Pentru MUX-uri de 16 cai alegem 74LS154