| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
| Navigatie |
|
STABILITATEA INITIALA A NAVEI |
Consideratii generale despre stabilitatea navei.
In general, un corp se gaseste in echilibru atunci cand rezultanta fortelor care actioneaza asupra lui si momentul rezultant sunt nule. Un corp care pluteste in apa linistita se afla in echilibru sub actiunea a doua forte rezultante verticale, egale si de sens contrar si actionand pe acelasi suport: forta de greutate, actionand vertical de jos in sus in centrul de greutate si forta de impingere orientata vertical in sus cu punct de actiune centrul de carena. Corpurile plutitoare pot exista in trei situatii de echilibru:
(a) Echilibru stabil, atunci cand corpul scos din pozitia de echilibru de o cauza externa, revine la pozitia initiala de indata ce cauza externa inceteaza sa actioneze.
(b) Echilibru instabil, atunci cand corpul scos din pozitia de echilibru de o cauza externa, nu mai revine la pozitia initiala dupa disparitia cauzei externe, departandu-se tot mai mult de aceasta pozitie.
(c) Echilibru indiferent sau neutru, atunci cand corpul scos din pozitia de echilibru de o cauza externa, ramane in pozitie deplasata chiar si dupa disparitia cauzei externe.
In cazul unei nave situatia de echilibru indiferent trebuie tratata tot ca o situatie de instabilitate, pentru ca nu putem accepta de exemplu, ca o nava inclinata transversal la tribord cu 10 de o cauza externa, sa ramana in aceasta pozitie, cand aceasta nu mai actioneaza . Asadar in 'Teoria navei' o nava poate fi in doua situatii: stabila sau instabila.
Ca
o consecinta a actiunii fortelor externe nava va putea capata
deplasari pe toate cele sase grade de libertate: trei translatii
in lungul axelor de coordonate ![]() si trei rotatii
in jurul acestor axe.
si trei rotatii
in jurul acestor axe.
Sa analizam in continuare din punct de vedere al stabilitatii deplasarea navei pe fiecare din cele sase grade de libertate.
Daca
scoatem nava din pozitia de echilibru deplasand-o pe directia axei ![]() , vom observa ca odata cu incetarea cauzei
exterioare nava revine la pozitia initiala deci este intr-o
situatie de echilibru stabil pe aceasta directie. Astfel daca
nava se deplaseaza vertical in sus, scade pescajul iar forta de
impingere arhimedica va deveni mai mica decat forta de greutate
care isi pastreaza constanta valoarea. Sub actiunea
fortei rezultante nava revine la pozitia de echilibru initial,
odata cu incetarea actiunii cauzei externe; dupa ce executa
cateva oscilatii verticale amortizate. Nava este in echilibru stabil pe
directia axei
, vom observa ca odata cu incetarea cauzei
exterioare nava revine la pozitia initiala deci este intr-o
situatie de echilibru stabil pe aceasta directie. Astfel daca
nava se deplaseaza vertical in sus, scade pescajul iar forta de
impingere arhimedica va deveni mai mica decat forta de greutate
care isi pastreaza constanta valoarea. Sub actiunea
fortei rezultante nava revine la pozitia de echilibru initial,
odata cu incetarea actiunii cauzei externe; dupa ce executa
cateva oscilatii verticale amortizate. Nava este in echilibru stabil pe
directia axei ![]() indiferent de
magnitudinea deplasarilor pe aceasta directie.
indiferent de
magnitudinea deplasarilor pe aceasta directie.
Daca
nava capata deplasari pe directiile axelor ![]() si
si ![]() , mediul marin opune rezistenta la aceste deplasari,
prin aparitia fortelor de rezistenta la inaintare care se
opun miscarii. Dupa disparitia fortelor exterioare,
nava ramane in pozitie deplasata si nu revine la pozitia
initiala. Aceasta comportare are loc indiferent de magnitudinea
deplasarilor in plan orizontal iar situatia este de echilibru
indiferent, deci nava este instabila pe aceste directii.
, mediul marin opune rezistenta la aceste deplasari,
prin aparitia fortelor de rezistenta la inaintare care se
opun miscarii. Dupa disparitia fortelor exterioare,
nava ramane in pozitie deplasata si nu revine la pozitia
initiala. Aceasta comportare are loc indiferent de magnitudinea
deplasarilor in plan orizontal iar situatia este de echilibru
indiferent, deci nava este instabila pe aceste directii.
Rotatia
navei in jurul axei ![]() (pivotarea) implica
deplasari in plan orizontal si aparitia unui moment rezistent la
rotatie din partea mediului marin. Dupa disparitia cauzei
externe, nava va ramane deplasata neputand reveni la pozitia initiala
indiferent de marimea deplasarii. Suntem din nou intr-un caz de
instabilitate.
(pivotarea) implica
deplasari in plan orizontal si aparitia unui moment rezistent la
rotatie din partea mediului marin. Dupa disparitia cauzei
externe, nava va ramane deplasata neputand reveni la pozitia initiala
indiferent de marimea deplasarii. Suntem din nou intr-un caz de
instabilitate.
In
cazul rotatiei navei in jurul axelor orizontale; longitudinala ![]() si transversala
si transversala
![]() , aceasta se poate gasi in oricare din situatiile
stabila sau instabila, totul depinzand de o serie intreaga de
factori cum ar fi: dimensiunile navei, forma suprafetei imerse, distributia
de greutati la bord si tipul acestora, precum si marimea
unghiului de inclinare. Spre exemplu, daca o nava pluteste
intr-o pozitie data si asupra ei actioneaza o cauza
externa care o scoate din aceasta pozitie inclinand-o
transversal, forta de impingere si forta de greutate vor forma
un cuplu, momentul acestuia putand avea semne diferite. Astfel, daca acest
moment tinde sa readuca nava in pozitia initiala are
semn pozitiv si se numeste moment
de redresare sau moment de
stabilitate, nava fiind stabila (Fig. 42,a). Atunci cand momentul
tinde sa incline nava in acelasi sens cu cel produs de cauza externa,
are semn negativ si se numeste moment
de instabilitate, nava fiind instabila (Fig. 42,b).
, aceasta se poate gasi in oricare din situatiile
stabila sau instabila, totul depinzand de o serie intreaga de
factori cum ar fi: dimensiunile navei, forma suprafetei imerse, distributia
de greutati la bord si tipul acestora, precum si marimea
unghiului de inclinare. Spre exemplu, daca o nava pluteste
intr-o pozitie data si asupra ei actioneaza o cauza
externa care o scoate din aceasta pozitie inclinand-o
transversal, forta de impingere si forta de greutate vor forma
un cuplu, momentul acestuia putand avea semne diferite. Astfel, daca acest
moment tinde sa readuca nava in pozitia initiala are
semn pozitiv si se numeste moment
de redresare sau moment de
stabilitate, nava fiind stabila (Fig. 42,a). Atunci cand momentul
tinde sa incline nava in acelasi sens cu cel produs de cauza externa,
are semn negativ si se numeste moment
de instabilitate, nava fiind instabila (Fig. 42,b).
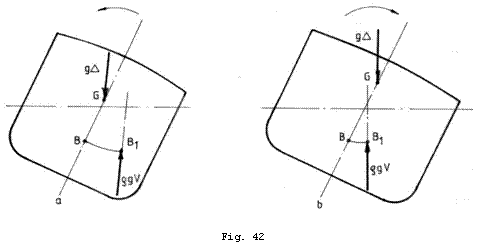
Mecanismul fizic al aparitiei momentului de redresare
este urmatorul. In decursul inclinarii navei centrul de carena
se va deplasa in sensul inclinarii in timp ce centrul de greutate ramane
in pozitie fixa, neavand loc deplasari de mase la bord.
Deplasarea relativa a celor doua centre aduce nava in situatia
in care, la sfarsitul inclinarii, forta de impingere si forta
de greutate raman egale in modulul, insa nu vor mai actiona pe
acelasi suport, determinand aparitia momentului de stabilitate.
Asa
cum vom demonstra in acest capitol pentru navele de suprafata la
aceeasi marime a unghiului de inclinare, momentul de stabilitate
longitudinala este mult mai mare decat momentul de stabilitate transversala.
Din acest considerent, in teoria navei se studiaza indeosebi stabilitatea
transversala in doua situatii: stabilitatea la unghiuri mici de
inclinare sau stabilitatea initiala; atunci cand unghiul de inclinare
transversala ![]() si stabilitatea
la unghiuri mari de inclinare. La unghiuri mici, momentul de stabilitate are o
variatie liniara cu unghiul de inclinare, pe cand la unghiuri mari de
inclinare aceasta ipoteza nu mai este valabila.
si stabilitatea
la unghiuri mari de inclinare. La unghiuri mici, momentul de stabilitate are o
variatie liniara cu unghiul de inclinare, pe cand la unghiuri mari de
inclinare aceasta ipoteza nu mai este valabila.
Spre deosebire de navele de suprafata, la submarinele complet imersate nu se poate face o distinctie ca ordin de marime intre stabilitatea transversala si cea longitudinala. Un submarin imersat se poate rasturna la fel de usor atat transversal cat si longitudinal. Aceasta diferenta de comportament intre navele de suprafata si submarinele imersate se explica prin aceea ca centrul de carena la submarine este fix, in timp ce la nave se deplaseaza odata cu inclinarea corpului.
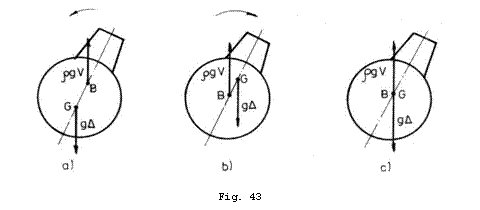
Un submarin se poate gasi din punct de vedere al stabilitatii in una din situatiile din Fig. 43.
Se poate observa ca numai in cazul din Fig. 43,a submarinul este stabil intrucat momentul creat de forta de impingere si forta de greutate tinde sa-l aduca in pozitia initiala. In concluzie, un corp imersat este in pozitie de echilibru stabil, daca centrul de greutate se gaseste sub centrul de carena.
Astfel in cazul navelor de suprafata cat si in cazul submarinelor asa cum se observa din figurile 42 si 43, stabilitatea se mareste daca centrul de greutate se deplaseaza pe verticala in jos. Daca nava este initial stabila, se mareste bratul momentului si implicit valoarea momentului de stabilitate. Daca nava este initial instabila, prin deplasarea centrului de greutate vertical in jos cu o distanta suficienta, se schimba sensul momentului transformandu-l din moment de instabilitate in moment de stabilitate.
Cauzele externe care determina inclinarea navei pot actiona static , atunci cand valoarea momentului exterior are o crestere lenta in timp si dinamic , atunci cand momentul exterior actioneaza cu intensitatea maxima din prima clipa. In teoria navei efectele acestor actiuni se studiaza separat, impartind stabilitatea navei in: stabilitate statica si stabilitate dinamica.
Stabilitatea statica este caracterizata de valoarea momentului de stabilitate, in timp ce masura stabilitatii dinamice este lucrul mecanic al momentului de stabilitate care se consuma in timpul inclinarii.
Inclinari izocarene. Teorema Euler
In general, actiunea unei cauze externe asupra navei se reduce la un torsor format dintr-o forta si un moment. Daca forta externa are componenta pe directie verticala nava isi modifica pescajul, pana cand forta de impingere egaleaza rezultanta fortelor verticale care actioneaza asupra ei. Daca forta externa actioneaza pe directie transversala nava capata o miscare de deriva intampinand din partea apei o forta de rezistenta. Apare in acest fel si un moment care inclina nava transversal. Atunci cand forta externa actioneaza pe directie longitudinala, apare un moment care inclina nava longitudinal. In ambele cazuri nava isi modifica pozitia in raport cu suprafata libera a apei pastrand constant volumul carenei. Doua plutiri se numesc izocarene daca ele corespund la volume de carene egale.
Considerand
doua plutiri izocarene ![]() si
si ![]() inclinate transversal,
una fata de alta, cu unghiul elementar
inclinate transversal,
una fata de alta, cu unghiul elementar ![]() ,vom observa ca
forma volumului carenei se modifica deoarece volumul
,vom observa ca
forma volumului carenei se modifica deoarece volumul ![]() intra in apa,
iar volumul
intra in apa,
iar volumul ![]() iese din apa.
Aceste doua volume in forma de pana se numesc onglete;
iese din apa.
Aceste doua volume in forma de pana se numesc onglete; ![]() este ongletul imers
iar
este ongletul imers
iar ![]() este ongletul emers
(Fig. 44). Cele doua plutiri fiind izocarene rezulta egalitatea:
este ongletul emers
(Fig. 44). Cele doua plutiri fiind izocarene rezulta egalitatea:
![]() (15.1)
(15.1)
Pentru
calculul celor doua volume, observam ca ele sunt delimitate de
dreapta de intersectie a plutirilor, a carei urma pe planul
transversal este punctul ![]() si care imparte
aria plutirii in doua (Fig. 45):
si care imparte
aria plutirii in doua (Fig. 45): ![]() este partea din aria plutirii care corespunde ongletului
imers iar
este partea din aria plutirii care corespunde ongletului
imers iar ![]() corespunde ongletului
corespunde ongletului
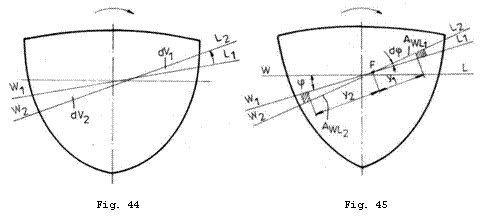
emers. In interiorul fiecarui
onglet consideram cate o prisma elementara avand ca baza ![]() iar ca inaltime
iar ca inaltime
![]() , respectiv
, respectiv ![]() .
.
Asadar:
![]() (15.2)
(15.2)
![]() (15.3)
(15.3)
![]() si
si ![]() sunt momentele statice
ale ariilor
sunt momentele statice
ale ariilor ![]() si
si ![]() in raport cu dreapta
de intersectie a plutirilor
in raport cu dreapta
de intersectie a plutirilor ![]() si
si ![]() . Introducem (15.2) si (15.3) in (15.1) si obtinem:
. Introducem (15.2) si (15.3) in (15.1) si obtinem:
![]()
sau
![]() (15.4)
(15.4)
In
relatia (15.4) ![]() reprezinta
momentul static al ariei plutirii
reprezinta
momentul static al ariei plutirii ![]() in raport cu dreapta
de intersectie a plutirilor
in raport cu dreapta
de intersectie a plutirilor ![]() si
si ![]() . Din relatia (15.4) rezulta ca acest moment
static este nul, ceea ce inseamna ca dreapta de intersectie (axa
de inclinare), trece prin centrul de greutate al plutirii
. Din relatia (15.4) rezulta ca acest moment
static este nul, ceea ce inseamna ca dreapta de intersectie (axa
de inclinare), trece prin centrul de greutate al plutirii ![]() . Aceasta este esenta teoremei Euler al carei enunt
este urmatorul:
. Aceasta este esenta teoremei Euler al carei enunt
este urmatorul:
Doua plutiri izocarene inclinate cu un unghi infinit mic, una fata de alta, se intersecteaza dupa o dreapta ce trece prin centrul de greutate al celor doua plutiri.
La navele cu borduri verticale teorema Euler este valabila pentru orice inclinare in limitele in care plutirile nu intersecteaza puntea sau gurna.
Putem formula o reciproca a teoremei Euler, deosebit de importanta:
Daca doua plutiri sunt inclinate cu un unghi infinit mic in jurul unei axe ce trece prin centrul plutirii, atunci cele doua plutiri sunt izocarene.
Deplasarea centrului de carena
Teorema lui Euler a fost demonstrata pentru o inclinare pur transversala. Acest lucru nu micsoreaza cu nimic generalitatea enuntului ei. In general o nava se poate roti in jurul oricarei axe centrale a plutirii cu un unghi infinit mic. Plutirea initiala si cea inclinata vor fi izocarene, insa centrele de carena vor fi puncte distincte, deoarece formele celor doua carene sunt diferite. Ne intereseaza sa studiem modul in care se deplaseaza centrul de carena in timpul acestor inclinari.
Aparitia
ongletelor, imers si emers, egale si de volum ![]() , poate fi considerata ca o modificare a formei carenei.
Se poate considera ca forma carenei corespunzatoare plutirii
, poate fi considerata ca o modificare a formei carenei.
Se poate considera ca forma carenei corespunzatoare plutirii ![]() , se obtine din carena corespunzatoare plutirii
, se obtine din carena corespunzatoare plutirii ![]() , prin deplasarea volumului
, prin deplasarea volumului ![]() din bordul emers in
bordul imers. Centrul de greutate al acestui volum se va deplasa pe distanta
din bordul emers in
bordul imers. Centrul de greutate al acestui volum se va deplasa pe distanta
![]() .
.
Din mecanica teoretica este cunoscuta urmatoarea teorema, ca o consecinta directa a teoremei momentelor: 'Daca in interiorul unui sistem format din mai multe corpuri, un corp se deplaseaza dupa o directie oarecare; centrul de greutate al sistemului se deplaseaza dupa o directie paralela si in acelasi sens. Raportul dintre deplasarea centrului de greutate al sistemului si deplasarea centrului de greutate al corpului, este egal cu raportul dintre masa corpului si masa sistemului de corpuri.'
Conform teoremei amintite putem scrie (vezi Fig. 46):
![]() (16.1)
(16.1)
![]() (16.2)
(16.2)
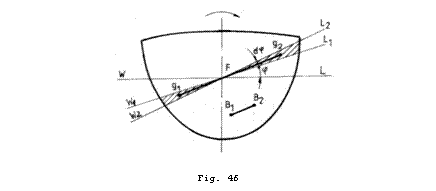 Daca
nava se inclina in jurul unei axe centrale oarecare din planul plutirii,
deplasarile
Daca
nava se inclina in jurul unei axe centrale oarecare din planul plutirii,
deplasarile ![]() si
si ![]() sunt spatiale si pot fi descompuse in trei deplasari
ortogonale corespunzatoare sistemului la care ne raportam.
sunt spatiale si pot fi descompuse in trei deplasari
ortogonale corespunzatoare sistemului la care ne raportam.
Sa
consideram un caz general de inclinare a navei in jurul unei axe centrale ![]() din planul plutirii
din planul plutirii ![]() (Fig. 47).
(Fig. 47).
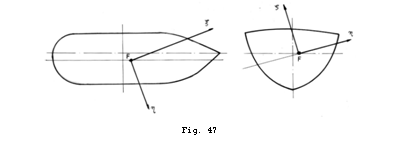
Sistemul
de axe triortogonal fata de care ne raportam, are planul ![]() care coincide cu
planul plutirii iar axa
care coincide cu
planul plutirii iar axa ![]() perpendiculara pe
acest plan.
perpendiculara pe
acest plan.
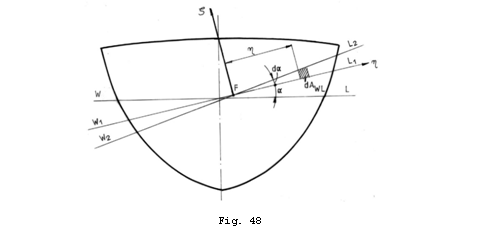
Ca urmare a inclinarii cu unghiul ![]() , deplasarea
, deplasarea ![]() a centrului de carena
poate fi descompusa in trei deplasari infinitezimale
a centrului de carena
poate fi descompusa in trei deplasari infinitezimale ![]() in lungul axelor.
Consideram un volum prismatic elementar ce are ca baza suprafata
elementara
in lungul axelor.
Consideram un volum prismatic elementar ce are ca baza suprafata
elementara ![]() iar ca inaltime
iar ca inaltime
![]() (Fig.48). Distantele
de la centrul de greutate al acestui volum la planele
(Fig.48). Distantele
de la centrul de greutate al acestui volum la planele ![]() si
si ![]() .
.
Prin deplasarea spatiala a centrului de carena au loc variatii ale momentelor statice ale volumului carenei in raport cu aceste plane, care se calculeaza cu formulele:
![]() (16.3)
(16.3)
![]() (16.4)
(16.4)
![]() (16.5)
(16.5)
Cele doua integrale care apar in relatiile anterioare reprezinta momentele de inertie ale ariei plutirii initiale, respectiv:
![]() (16.6)
(16.6)
- momentul de inertie centrifugal al suprafetei plutirii;
![]() (16.7)
(16.7)
- momentul de inertie al
suprafetei plutirii in raport cu axa centrala ![]() .
.
Deplasarile infinitezimale ale centrului de carena se vor scrie:
![]() (16.8)
(16.8)
![]() (16.9)
(16.9)
![]() (16.10)
(16.10)
Scriind relatia (16.10), tragem urmatoarele concluzii:
1)
La inclinari izocarene pe directie verticala, centrul de carena
se va deplasa intotdeauna in sus deoarece ![]() .
.
2)
Deplasarea pe directie verticala a centrului de carena ![]() , este un infinit mic de ordinul doi, comparativ cu deplasarile
in plan orizontal
, este un infinit mic de ordinul doi, comparativ cu deplasarile
in plan orizontal ![]() si
si ![]() .
.
Prin
urmare arcul elementar ![]() se poate calcula cu
relatia :
se poate calcula cu
relatia :
![]() (16.11)
(16.11)
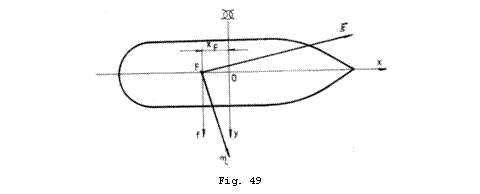
Sa
examinam in continuare separat inclinarile transversale si
longitudinale, presupunand ca plutirea initiala este dreapta,
adica ![]() . Situatia este prezentata in figura 49.
. Situatia este prezentata in figura 49.
A)
In cazul inclinarilor transversale, axa de inclinare ![]() . Momentele de inertie ale plutirii vor fi:
. Momentele de inertie ale plutirii vor fi:
![]()
Deplasarile elementare ale centrului de carena se pot calcula cu relatiile:
![]() (16.12)
(16.12)
![]() (16.13)
(16.13)
![]() (16.14)
(16.14)
In
formulele de mai sus, momentul de inertie centrifugal ![]() s-a considerat egal cu
zero, deoarece
s-a considerat egal cu
zero, deoarece ![]() este axa de simetrie a suprafetei plutirii iar
este axa de simetrie a suprafetei plutirii iar ![]() .
.
B)
In cazul inclinarilor longitudinale, axa de inclinare ![]() si
si ![]() iar unghiul de
inclinare
iar unghiul de
inclinare ![]() .
.
Momentele de inertie ale plutirii vor fi corespunzator:
![]()
Deplasarile elementare ale centrului de carena se calculeaza cu relatiile:
![]() (16.15)
(16.15)
![]() (16.16)
(16.16)
![]() (16.17)
(16.17)
Formulele
(16.8), (16.9) si (16.10) reprezinta modelul matematic al deplasarii
centrului de carena la inclinari infinit de mici, izocarene in jurul
unei axe centrale din planul plutirii. Ne putem imagina insa o infinitate
de inclinari, infinit mici, in jurul unei axe centrale de la 0 la 360,
precum si o infinitate de axe centrale situate in planul plutirii in jurul
carora se roteste nava. Locul geometric al centrelor de carena,
corespunzatoare acestor infinitati de plutiri izocarene, poarta
numele de suprafata centrelor de
carena sau suprafata ![]() . Daca ne fixam asupra unei axe centrale de
rotatie centrul de carena se va deplasa pe o curba de pe aceasta
suprafata care se numeste curba
centrelor de carena sau curba
. Daca ne fixam asupra unei axe centrale de
rotatie centrul de carena se va deplasa pe o curba de pe aceasta
suprafata care se numeste curba
centrelor de carena sau curba ![]() .
.
Studiind
relatia (16.11) vom observa ca la inclinari infinit mici
izocarene, centrul de carena se deplaseaza dupa directiile ![]() si
si ![]() deci intr-un plan
paralel cu planul plutirii, tangent la suprafata
deci intr-un plan
paralel cu planul plutirii, tangent la suprafata ![]() . Rezulta de aici o proprietate importanta a
suprafetei centrelor de carena, considerata de multi autori
ca teorema a II-a a lui Euler: 'Planul tangent la suprafata centrelor
de carena este paralel cu planul plutirii corespunzatoare punctului
de tangenta.'
. Rezulta de aici o proprietate importanta a
suprafetei centrelor de carena, considerata de multi autori
ca teorema a II-a a lui Euler: 'Planul tangent la suprafata centrelor
de carena este paralel cu planul plutirii corespunzatoare punctului
de tangenta.'
Metacentre si raze metacentrice
Sa revenim la inclinarile izocarene cu un unghi infinit mic, studiind separat inclinarile transversale si longitudinale.
In
timpul inclinarilor transversale, deplasarile elementare ale
centrului de carena se calculeaza cu formulele (16.12), (16.13) si
(16.14) observand ca ![]() . Rezulta ca centrul de carena se va deplasa
dupa o curba de pe suprafata
. Rezulta ca centrul de carena se va deplasa
dupa o curba de pe suprafata ![]() situata intr-un
plan paralel cu planul de inclinare
situata intr-un
plan paralel cu planul de inclinare ![]() .
.
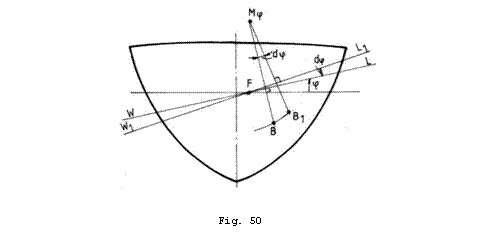
Se
considera o nava inclinata transversal cu unghiul ![]() si care fata
de aceasta pozitie, sufera o inclinare transversala
suplimentara cu unghiul
si care fata
de aceasta pozitie, sufera o inclinare transversala
suplimentara cu unghiul ![]() (Fig.50). Centrul de
carena se va deplasa parcurgand arcul elementar
(Fig.50). Centrul de
carena se va deplasa parcurgand arcul elementar ![]() , situat pe suprafata
, situat pe suprafata ![]() intr-un plan
transversal.
intr-un plan
transversal.
In
punctele ![]() si
si ![]() actioneaza
fortele de impingere ce corespund plutirilor
actioneaza
fortele de impingere ce corespund plutirilor ![]() si
si ![]() , perpendicular pe aceste plane. Intrucat planele plutirilor
sunt perpendiculare pe planul transversal in care se situeaza
, perpendicular pe aceste plane. Intrucat planele plutirilor
sunt perpendiculare pe planul transversal in care se situeaza ![]() si
si ![]() , rezulta ca suporturile fortelor de impingere
arhimedica sunt coplanare si se intersecteaza intr-un punct
, rezulta ca suporturile fortelor de impingere
arhimedica sunt coplanare si se intersecteaza intr-un punct ![]() .
.
Conform
teoremei a II-a a lui Euler, demonstrata in paragraful anterior, planele
tangente in punctele ![]() si
si ![]() la suprafata
la suprafata ![]() , sunt paralele cu
, sunt paralele cu ![]() , respectiv
, respectiv ![]() ; deci suporturile fortelor de impingere sunt
perpendiculare pe aceste plane. Rezulta ca pozitia limita a
punctului
; deci suporturile fortelor de impingere sunt
perpendiculare pe aceste plane. Rezulta ca pozitia limita a
punctului ![]() atunci cand
atunci cand ![]() este centrul de curbura
al curbei centrelor de carena in puncul
este centrul de curbura
al curbei centrelor de carena in puncul ![]() . El poarta denumirea de metacentru transversal iar raza de curbura se numeste raza metacentrica transversala
corespunzatoare unghiului
. El poarta denumirea de metacentru transversal iar raza de curbura se numeste raza metacentrica transversala
corespunzatoare unghiului ![]() de inclinare si
se noteaza cu
de inclinare si
se noteaza cu ![]() .
.
Din
(16.11), (16.12) si (16.13) se deduce expresia arcului elementar ![]() sub forma:
sub forma:
![]() (17.1)
(17.1)
unde ![]() este momentul de inertie al plutirii
este momentul de inertie al plutirii ![]() in raport cu o axa
paralela cu axa
in raport cu o axa
paralela cu axa ![]() ce trece prin centrul
ce trece prin centrul ![]() al acestei plutiri. Din (17.1) obtinem formula de calcul
pentru raza metacentrica transversala:
al acestei plutiri. Din (17.1) obtinem formula de calcul
pentru raza metacentrica transversala:
![]() (17.2)
(17.2)
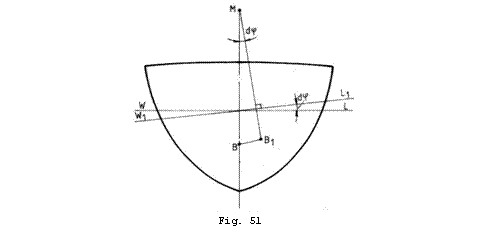
In situatia in care plutirea initiala este dreapta (Fig. 51) raza metacentrica transversala se calculeaza cu relatia:
![]() (17.3)
(17.3)
O
discutie asemanatoare se face pentru punerea in evidenta
a metacentrului longitudinal ![]() si a razei
metacentrice longitudinale. Intrucat stabilitatea longitudinala a navei se
studiaza in limita unghiurilor mici de inclinare, vom reduce discutia
la cazul plutirii initiale drepte
si a razei
metacentrice longitudinale. Intrucat stabilitatea longitudinala a navei se
studiaza in limita unghiurilor mici de inclinare, vom reduce discutia
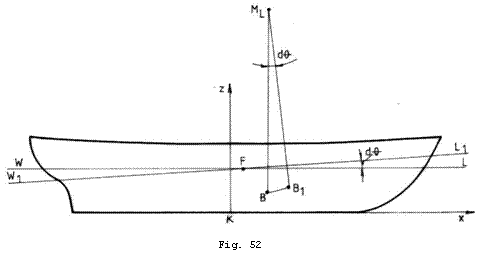
la cazul plutirii initiale drepte ![]() . Situatia este prezentata in Fig. 52.
. Situatia este prezentata in Fig. 52.
Cand nava se inclina longitudinal cu
unghiul ![]() centrul de carena
contureaza arcul elementar
centrul de carena
contureaza arcul elementar ![]() . Utilizand formulele (16.11), (16.15) si (16.16) gasim:
. Utilizand formulele (16.11), (16.15) si (16.16) gasim:
![]() (17.4)
(17.4)
iar pentru raza metacentrica longitudinala :
![]() (17.5)
(17.5)
In
practica se observa ca pentru o nava de suprafata,
raza metacentrica longitudinala ![]() este mult mai mare
decat raza metacentrica transversala
este mult mai mare
decat raza metacentrica transversala ![]() . In timp ce
. In timp ce ![]() are ordinul de marime
al lungimii navei , putand ajunge pana la
are ordinul de marime
al lungimii navei , putand ajunge pana la ![]() sau chiar
sau chiar ![]() ;
; ![]() variaza intre
variaza intre ![]() . La aceeasi concluzie putem ajunge studiind raportul
dintre
. La aceeasi concluzie putem ajunge studiind raportul
dintre ![]() si
si ![]() pentru un ponton paralelipipedic, cu dimensiunile
pentru un ponton paralelipipedic, cu dimensiunile ![]() .
.
Razele metacentrice vor fi:
![]() (17.6)
(17.6)
Raportul lor va fi :
![]() (17.7)
(17.7)
Cum ![]() variaza in limitele
variaza in limitele ![]() ;
; ![]() este situat in
limitele
este situat in
limitele ![]() .
.
Din relatiile (17.6) rezulta:
![]() (17.8)
(17.8)
care implica o variatie hiperbolica a inaltimilor metacentrice cu pescajul pontonului. In cazul navelor obisnuite, se remarca o variatie apropiata de cea hiperbolica, a inaltimilor metacentrice transversala si longitudinala cu pescajul.
Moment de redresare. Formula metacentrica a stabilitatii.
Inaltimi metacentrice
Asa cum am aratat in 14 mecanismul fizic al aparitiei momentului de redresare in cazul inclinarilor izocarene, consta in interactiunea dintre forta de impingere arhimedica si forta de greutate; datorita deplasarii centrului de carena in sensul inclinarii.
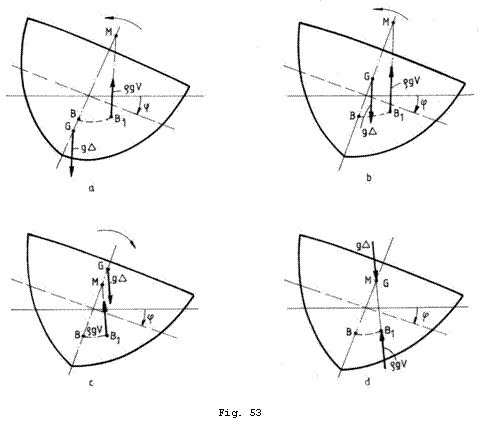
Considerand inclinari izocarene ale navei in limita unghiurilor mici, o nava se poate gasi din punct de vedere al stabilitatii transversale in una din situatiile prezentate in Fig. 53.
Cazul a (Fig. 53). Centrul de greutate
se gaseste sub centrul de carena. Cand nava se inclina
transversal, centrul de carena se deplaseaza in pozitia ![]() . Momentul cuplului format de forta de greutate
. Momentul cuplului format de forta de greutate ![]() si forta de
impingere
si forta de
impingere ![]() tinde sa aduca
nava in pozitia initiala, fiind un moment de stabilitate. Nava
se afla in acest caz intr-o situatie de stabilitate transversala
excesiva intalnita la navele unde se iau masuri speciale privind
stabilitatea cum sunt navele de sport si agrement. O nava cu
stabilitate excesiva executa oscilatii
dure pe o mare dezvoltata; adica oscilatii cu perioada
mica si frecventa mare. In timpul acestor miscari
apar forte de inertie mari; care pe de-o parte incarca structural nava, iar pe de alta parte actioneaza
asupra mecanismelor, instalatiilor si aparatelor de conducere ale
navei, putand duce la functionarea defectuoasa a acestora.
tinde sa aduca
nava in pozitia initiala, fiind un moment de stabilitate. Nava
se afla in acest caz intr-o situatie de stabilitate transversala
excesiva intalnita la navele unde se iau masuri speciale privind
stabilitatea cum sunt navele de sport si agrement. O nava cu
stabilitate excesiva executa oscilatii
dure pe o mare dezvoltata; adica oscilatii cu perioada
mica si frecventa mare. In timpul acestor miscari
apar forte de inertie mari; care pe de-o parte incarca structural nava, iar pe de alta parte actioneaza
asupra mecanismelor, instalatiilor si aparatelor de conducere ale
navei, putand duce la functionarea defectuoasa a acestora.
Cazul b (Fig. 53). In pozitia initiala
centrul de greutate este situat deasupra centrului de carena. In pozitie
inclinata transversal, centrul de carena se gaseste in ![]() . Momentul cuplului format de forta de greutate
. Momentul cuplului format de forta de greutate ![]() si forta
arhimedica
si forta
arhimedica ![]() tinde sa aduca
nava in pozitia initiala fiind un moment de stabilitate. Aceasta
pozitie relativa a celor trei centre, metacentrul transversal
tinde sa aduca
nava in pozitia initiala fiind un moment de stabilitate. Aceasta
pozitie relativa a celor trei centre, metacentrul transversal ![]() , centrul de greutate
, centrul de greutate ![]() , centrul de carena
, centrul de carena ![]() , dispuse in aceasta ordine pe verticala de sus in
jos, indica o situatie de stabilitate pozitiva si este
intalnita la marea majoritate a navelor in timpul exploatarii.
, dispuse in aceasta ordine pe verticala de sus in
jos, indica o situatie de stabilitate pozitiva si este
intalnita la marea majoritate a navelor in timpul exploatarii.
Cazul c (Fig. 53). In pozitia initiala
centrul de greutate este situat deasupra centrului de carena. Cand nava
este inclinata transversal, centrul de carena se deplaseaza din ![]() in
in ![]() astfel incat
metacentrul transversal
astfel incat
metacentrul transversal ![]() este pozitionat
sub centrul de greutate. Momentul cuplului format de forta de greutate
este pozitionat
sub centrul de greutate. Momentul cuplului format de forta de greutate ![]() si forta
arhimedica
si forta
arhimedica ![]() este orientat in
sensul inclinarii deci este un moment de instabilitate, nava gasindu-se intr-o situatie de
stabilitate negativa.
este orientat in
sensul inclinarii deci este un moment de instabilitate, nava gasindu-se intr-o situatie de
stabilitate negativa.
Cazul d (Fig. 53). In pozitia initiala
centrul de greutate se afla deasupra centrului de carena. Pentru o
inclinare transversala centrul de carena se deplaseaza din ![]() in
in ![]() , pozitie pentru care metacentrul transversal
, pozitie pentru care metacentrul transversal ![]() coincide cu centrul de
greutate
coincide cu centrul de
greutate ![]() . In acest caz momentul este nul si nava ramane in
pozitie inclinata, situatia fiind de asemenea de instabilitate.
. In acest caz momentul este nul si nava ramane in
pozitie inclinata, situatia fiind de asemenea de instabilitate.
Cazul c (Fig. 53). In pozitia initiala
centrul de greutate este situat deasupra centrului de carena. Cand nava
este inclinata transversal, centrul de carena se deplaseaza din ![]() in
in ![]() astfel incat
metacentrul transversal
astfel incat
metacentrul transversal ![]() este pozitionat
sub centrul de greutate. Momentul cuplului format de forta de greutate
este pozitionat
sub centrul de greutate. Momentul cuplului format de forta de greutate ![]() si forta
arhimedica
si forta
arhimedica ![]() este orientat in
sensul inclinarii deci este un moment de instabilitate, nava gasindu-se intr-o situatie de
stabilitate negativa.
este orientat in
sensul inclinarii deci este un moment de instabilitate, nava gasindu-se intr-o situatie de
stabilitate negativa.
Cazul d (Fig. 53). In pozitia initiala
centrul de greutate se afla deasupra centrului de carena. Pentru o
inclinare transversala centrul de carena se deplaseaza din ![]() in
in ![]() , pozitie pentru care metacentrul transversal
, pozitie pentru care metacentrul transversal ![]() coincide cu centrul de
greutate
coincide cu centrul de
greutate ![]() . In acest caz momentul este nul si nava ramane in
pozitie inclinata, situatia fiind de asemenea de instabilitate.
. In acest caz momentul este nul si nava ramane in
pozitie inclinata, situatia fiind de asemenea de instabilitate.
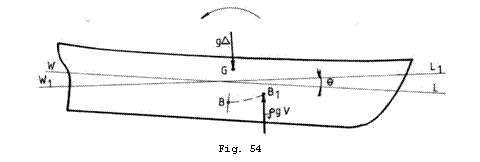
Din punctul de vedere al mecanismului fizic de aparitie a momentului de stabilitate exista o analogie perfecta intre stabilitatea transversala si stabilitatea longitudinala a navei. In Fig. 54 este prezentat cazul cel mai frecvent in care se poate gasi o nava din punct de vedere al stabilitatii longitudinale.
Vom face observatia ca o nava de
suprafata obisnuita nu va fi niciodata instabila
longitudinal deoarece ![]() si totdeauna
metacentrul longitudinal va fi situat deasupra centrului de greutate.
si totdeauna
metacentrul longitudinal va fi situat deasupra centrului de greutate.
Ne propunem in continuare sa gasim formule pentru calculul momentelor de stabilitate transversala si longitudinala.
Consideram
o nava inclinata transversal cu unghiul infinit mic ![]() (Fig. 55).
(Fig. 55).
Initial centrele![]() ,
,![]() si
si ![]() se gasesc in
se gasesc in ![]() In timpul inclinarii
In timpul inclinarii
![]() se deplaseaza in pozitia
se deplaseaza in pozitia ![]() care corespunde
plutirii
care corespunde
plutirii ![]() . In
. In ![]() actioneaza
vertical in sus forta de impingere arhimedica. Suportul acestei forte
intersecteaza
actioneaza
vertical in sus forta de impingere arhimedica. Suportul acestei forte
intersecteaza ![]() in metacentrul transversal
in metacentrul transversal ![]() . Fata de pozitia corespunzatoare
plutirii initiale
. Fata de pozitia corespunzatoare
plutirii initiale ![]() cand forta
arhimedica
cand forta
arhimedica ![]() si forta de
greutate
si forta de
greutate ![]() actionau pe acelasi
suport, in cazul plutirii inclinate cele doua forte formeaza un
cuplu. Momentul corespunzator acestui cuplu este un moment de stabilitate
elementar care se calculeaza cu formula :
actionau pe acelasi
suport, in cazul plutirii inclinate cele doua forte formeaza un
cuplu. Momentul corespunzator acestui cuplu este un moment de stabilitate
elementar care se calculeaza cu formula :
![]() (18.1)
(18.1)
unde ![]() este bratul
acestui moment elementar. Din Fig. 55 se observa ca putem scrie:
este bratul
acestui moment elementar. Din Fig. 55 se observa ca putem scrie:
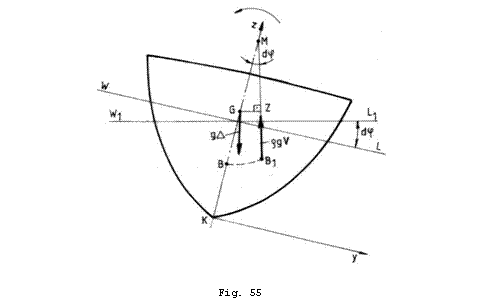
![]() (18.2)
(18.2)
si mai departe dupa inlocuire
![]() (18.3)
(18.3)
Distanta
![]() reprezinta inaltimea
metacentrica transversala si este o masura a stabilitatii
initiale a navei. Inaltimea metacentrica se considera
pozitiva cand metacentrul transversal este situat deasupra centrului de
greutate si negativa cand metacentrul transversal este situat sub
centrul de greutate. Inaltimea metacentrica se poate scrie si
ca diferenta dintre cota metacentrului transversal si cota centrului
de greutate.
reprezinta inaltimea
metacentrica transversala si este o masura a stabilitatii
initiale a navei. Inaltimea metacentrica se considera
pozitiva cand metacentrul transversal este situat deasupra centrului de
greutate si negativa cand metacentrul transversal este situat sub
centrul de greutate. Inaltimea metacentrica se poate scrie si
ca diferenta dintre cota metacentrului transversal si cota centrului
de greutate.
![]() (18.4)
(18.4)
sau
![]() (18.5)
(18.5)
Relatia (18.3) se numeste formula metacentrica a stabilitatii transversale sub forma diferentiala . Chiar daca aceasta formula a fost dedusa pentru o inclinare transversala infinitezimala ea poate fi aplicata si pentru unghiuri finite considerate in categoria unghiurilor mici de inclinare; sub forma
![]() (18.6)
(18.6)
In
relatia (18.6) unghiul ![]() se masoara
in radiani iar limitele de valabilitate practica sunt pentru
se masoara
in radiani iar limitele de valabilitate practica sunt pentru ![]() .
.
Discutand in continuare despre stabilitatea longitudinala la unghiuri mici de inclinare si rationand asemanator se obtine formula metacentrica a stabilitatii longitudinale sub forma diferentiala
![]() (18.7)
(18.7)
sau pentru unghiuri finite de inclinare longitudinala
![]() (18.8)
(18.8)
cu unghiul de inclinare
longitudinala ![]() exprimat in radiani.
exprimat in radiani.
Distanta
![]() este inaltimea
metacentrica longitudinala si este o masura a stabilitatii
longitudinale a navei. Ea se poate exprima si ca diferenta dintre
cota metacentrului longitudinal si cota centrului de greutate
este inaltimea
metacentrica longitudinala si este o masura a stabilitatii
longitudinale a navei. Ea se poate exprima si ca diferenta dintre
cota metacentrului longitudinal si cota centrului de greutate
![]() (18.9)
(18.9)
sau
![]() (18.10)
(18.10)
Analizand
prin intermediul formulei metacentrice a stabilitatii transversale
cazurile prezentate in Fig. 53, se constata ca in cazurile a) si
b) ![]() deoarece
deoarece ![]() , in cazul c)
, in cazul c) ![]() (
(![]() ) si in cazul d)
) si in cazul d) ![]() (
(![]() ).
).
Din
punct de vedere al stabilitatii transversale a navei este de dorit o
valoare cat mai mare a inaltimii metacentrice ![]() . Pe de alta parte o nava cu
. Pe de alta parte o nava cu ![]() mare executa pe mare reala oscilatii de ruliu
foarte 'dure'; adica oscilatii cu perioada mica si
frecventa mare. Astfel de miscari implica forte
de inertie mari care actioneaza asupra mecanismelor si
instalatiilor de la bord, precum si asupra aparatelor de conducere a
navei. Nu in ultima instanta, se inrautatesc
conditiile de viata ale echipajului. Din aceste motive in timpul
proiectarii navei se are in vedere ca sa se asigure o valoare a inaltimii
metacentrice transversale in conformitate cu tipul navei si cu normele de
registru.
mare executa pe mare reala oscilatii de ruliu
foarte 'dure'; adica oscilatii cu perioada mica si
frecventa mare. Astfel de miscari implica forte
de inertie mari care actioneaza asupra mecanismelor si
instalatiilor de la bord, precum si asupra aparatelor de conducere a
navei. Nu in ultima instanta, se inrautatesc
conditiile de viata ale echipajului. Din aceste motive in timpul
proiectarii navei se are in vedere ca sa se asigure o valoare a inaltimii
metacentrice transversale in conformitate cu tipul navei si cu normele de
registru.
Asa
cu am precizat, inaltimile metacentrice, transversala si
longitudinala, corespund inclinarilor navei in jurul axelor centrale
situate in planul plutirii, ![]() si
si ![]() . Vom remarca faptul ca momentul de inertie al
plutirii in raport cu oricare axa centrala are valoarea situata
intre
. Vom remarca faptul ca momentul de inertie al
plutirii in raport cu oricare axa centrala are valoarea situata
intre ![]() si
si ![]() ; motiv pentru care inaltimea metacentrica
corespunzatoare rotatiei in jurul acestei axe este mai mare decat inaltimea
metacentrica transversala
; motiv pentru care inaltimea metacentrica
corespunzatoare rotatiei in jurul acestei axe este mai mare decat inaltimea
metacentrica transversala ![]() si mai mica
decat inaltimea metacentrica longitudinala
si mai mica
decat inaltimea metacentrica longitudinala ![]() . De asemenea, am aratat ca datorita faptului
ca
. De asemenea, am aratat ca datorita faptului
ca ![]() , pentru navele de suprafata problema stabilitatii
navei nu se pune decat in plan transversal. In ceea ce priveste
stabilitatea longitudinala a unei nave de suprafata neavariate,
principalele probleme care se pun sunt legate de determinarea asietei si a
pescajului sub actiunea diferitelor cauze externe ce pot aparea in
timpul exploatarii. O inclinare longitudinala mica a navei, va
determina o deplasare a centrului de carena in directia inclinarii
suficient de mare astfel incat momentul format de forta de impingere si
forta de greutate sa fie suficient de mare comparativ cu momentul
produs de aceleasi forte la o inclinare egala in plan
transversal. Daca totusi in timpul exploatarii apar cauze care
determina o deplasare a centrului de greutate pe verticala in sus,
micsorand stabilitatea navei atunci aceasta se va putea rasturna in
plan transversal cu mult inainte de aparitia pericolului de rasturnare
longitudinala, pentru ca
, pentru navele de suprafata problema stabilitatii
navei nu se pune decat in plan transversal. In ceea ce priveste
stabilitatea longitudinala a unei nave de suprafata neavariate,
principalele probleme care se pun sunt legate de determinarea asietei si a
pescajului sub actiunea diferitelor cauze externe ce pot aparea in
timpul exploatarii. O inclinare longitudinala mica a navei, va
determina o deplasare a centrului de carena in directia inclinarii
suficient de mare astfel incat momentul format de forta de impingere si
forta de greutate sa fie suficient de mare comparativ cu momentul
produs de aceleasi forte la o inclinare egala in plan
transversal. Daca totusi in timpul exploatarii apar cauze care
determina o deplasare a centrului de greutate pe verticala in sus,
micsorand stabilitatea navei atunci aceasta se va putea rasturna in
plan transversal cu mult inainte de aparitia pericolului de rasturnare
longitudinala, pentru ca ![]() este situat mai sus pe verticala decat
este situat mai sus pe verticala decat ![]() . Este putin probabil ca o nava de suprafata
neavariata sa intalneasca o asemenea forta pe directie
verticala, care sa-i deplaseze
. Este putin probabil ca o nava de suprafata
neavariata sa intalneasca o asemenea forta pe directie
verticala, care sa-i deplaseze ![]() deasupra lui
deasupra lui ![]() nava devenind instabila si in plan longitudinal.
nava devenind instabila si in plan longitudinal.
Navele de suprafata se pot rasturna longitudinal doar ca urmare a inundarii unui compartiment sau a unui grup de compartimente situate la extremitatile pupa sau prova ale navei, datorita unei avarii. Patrunderea unei cantitati mari de apa in interiorul navei la una din extremitatile prova sau pupa, va exclude din flotabilitatea navei zona corespunzatore compartimentului inundat, deplasand centrul de carena in sens opus in timp ce centrul de greutate ramane in aceeasi pozitie, iar momentul determinat de forta de impingere si forta de greutate ajunge asa de mare incat poate rasturna nava longitudinal.
Spre deosebire de o nava de suprafata, un submarin imersat se poate rasturna la fel de usor pe directie longitudinala ca pe directie transversala. Aceasta deosebire de comportament se datoreaza faptului ca la submarinele complet imersate, centrul de carena ramane in permanenta un punct fix.
In concluzie, pentru ca o nava sa
aiba stabilitate pozitiva pe carena dreapta este necesar ca
metacentrul transversal sa fie deasupra centrului de greutate ![]() . Se spune ca in aceasta situatie inaltimea
metacentrica transversala este pozitiva
. Se spune ca in aceasta situatie inaltimea
metacentrica transversala este pozitiva ![]() . In acest caz daca o cauza externa scoate
nava din pozitia de echilibru; dupa ce cauza externa inceteaza
sa actioneze, nava va reveni la pozitia initiala
datorita cuplului format de forta de impingere arhimedica si
forta de greutate.
. In acest caz daca o cauza externa scoate
nava din pozitia de echilibru; dupa ce cauza externa inceteaza
sa actioneze, nava va reveni la pozitia initiala
datorita cuplului format de forta de impingere arhimedica si
forta de greutate.
Cand ![]() , inaltimea metacentrica este nula
, inaltimea metacentrica este nula ![]() , bratul cuplului si implicit cuplul vor fi nule.
Dupa ce cauza externa care a inclinat nava inceteaza sa actioneze,
aceasta ramane in pozitie inclinata. In sens 'mecanic'
suntem intr-o pozitie de echilibru indiferent, dar in realitate este o
situatie de stabilitate negativa sau instabilitate.
, bratul cuplului si implicit cuplul vor fi nule.
Dupa ce cauza externa care a inclinat nava inceteaza sa actioneze,
aceasta ramane in pozitie inclinata. In sens 'mecanic'
suntem intr-o pozitie de echilibru indiferent, dar in realitate este o
situatie de stabilitate negativa sau instabilitate.
Cand ![]() , metacentrul transversal este situat sub centrul de
greutate; inaltimea metacentrica este negativa
, metacentrul transversal este situat sub centrul de
greutate; inaltimea metacentrica este negativa ![]() si implicit
momentul cuplului format de cele doua forte. Acest moment va avea
sensul momentului exterior ajutand la inclinarea navei. Suntem de asemenea
intr-o situatie de stabilitate negativa sau instabilitate.
si implicit
momentul cuplului format de cele doua forte. Acest moment va avea
sensul momentului exterior ajutand la inclinarea navei. Suntem de asemenea
intr-o situatie de stabilitate negativa sau instabilitate.
Momentul stabilitatii de forma si momentul stabilitatii de greutate
Daca asupra unui corp actioneaza un cuplu de forte si cunoastem marimea fortelor, directia si punctele de aplicatie, este posibil sa descompunem acest cuplu in doua componente; aplicand in orice punct de pe corp doua forte egale, paralele si de sens contrar cu cele care formeaza cuplul.
Urmam
aceasta procedura pentru o nava inclinata in sens
transversal cu unghiul ![]() si aplicam
in centrul de carena initial
si aplicam
in centrul de carena initial ![]() doua forte
paralele, egale si de sens contrar cu forta de greutate a navei
doua forte
paralele, egale si de sens contrar cu forta de greutate a navei ![]() si impingerea
arhimedica
si impingerea
arhimedica ![]() . Obtinem doua cupluri de sens contrar avand bratele
. Obtinem doua cupluri de sens contrar avand bratele
![]() , respectiv
, respectiv ![]() . Cu referire la Fig. 56 considerand unghiul
. Cu referire la Fig. 56 considerand unghiul ![]() in categoria
unghiurilor mici, aceste brate se calculeaza cu formulele (19.1),
(19.2):
in categoria
unghiurilor mici, aceste brate se calculeaza cu formulele (19.1),
(19.2):
![]() (19.1)
(19.1)
![]() (19.2)
(19.2)
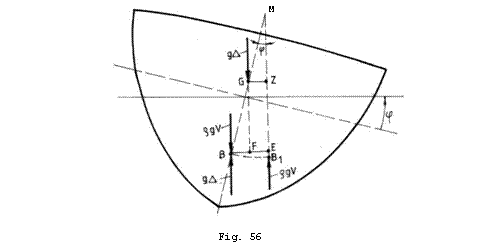
Momentul de stabilitate va fi egal cu diferenta momentelor celor doua cupluri:
![]() (19.3)
(19.3)
Primul dintre ele se noteaza
cu ![]() si se numeste
momentul stabilitatii de forma
si se numeste
momentul stabilitatii de forma
![]() (19.4)
(19.4)
iar al doilea se noteaza cu ![]() si se numeste
momentul stabilitatii de
greutate
si se numeste
momentul stabilitatii de
greutate
![]() (19.5)
(19.5)
In corespondenta ![]() se noteaza cu
se noteaza cu ![]() si se numeste bratul
stabilitatii de forma , respectiv
si se numeste bratul
stabilitatii de forma , respectiv ![]() se noteaza cu
se noteaza cu ![]() si se numeste
bratul stabilitatii de
greutate.
si se numeste
bratul stabilitatii de
greutate.
La
acelasi rezultat se poate ajunge plecand de la distributia reala
de presiuni pe suprafata ![]() a corpului navei. Daca
nava se inclina transversal cu unghiul
a corpului navei. Daca
nava se inclina transversal cu unghiul ![]() fiecare punct de pe
suprafata
fiecare punct de pe
suprafata ![]() isi va modifica
pescajul cu cantitatea
isi va modifica
pescajul cu cantitatea ![]() si corespunzator
presiunea cu:
si corespunzator
presiunea cu:
![]() (19.6)
(19.6)
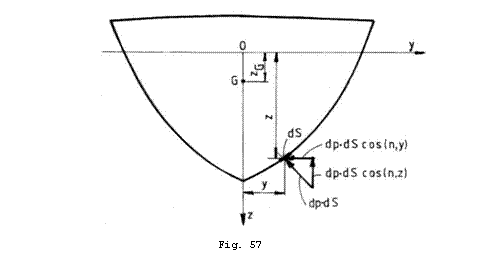
Ca sa calculam momentul in
raport cu axa ![]() aducem nava pe carena
dreapta, o incarcam cu aceasta variatie de presiuni si
consideram axa
aducem nava pe carena
dreapta, o incarcam cu aceasta variatie de presiuni si
consideram axa ![]() verticala si
pozitiva in jos (Fig.57).
verticala si
pozitiva in jos (Fig.57).
Acest moment are forma matematica
![]() (19.7)
(19.7)
Momentul ![]() este calculat fata de axa
este calculat fata de axa ![]() . Momentul de stabilitate
. Momentul de stabilitate ![]() se calculeaza in
raport cu o axa paralela cu axa
se calculeaza in
raport cu o axa paralela cu axa ![]() ce trece prin centrul
de greutate al navei si are expresia:
ce trece prin centrul
de greutate al navei si are expresia:
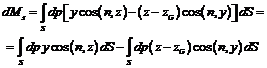 (19.8)
(19.8)
unde ![]() este adancimea
centrului de greutate al navei.
este adancimea
centrului de greutate al navei.
Primul termen din relatia (19.8) reprezinta momentul datorat fortelor verticale de presiune suplimentara iar al doilea reprezinta momentul componentelor orizontale.
Pe de alta parte ![]() si
si ![]() in care
in care ![]() este proiectia
suprafetei elementare de pe corpul navei pe planul plutirii si
este proiectia
suprafetei elementare de pe corpul navei pe planul plutirii si ![]() este proiectia
aceleasi suprafete pe planul diametral
este proiectia
aceleasi suprafete pe planul diametral ![]() Tinand cont de aceste observatii si inlocuind
(19.6) in (19.8) rezulta:
Tinand cont de aceste observatii si inlocuind
(19.6) in (19.8) rezulta:
![]() (19.9)
(19.9)
Se observa usor ca ![]() si apeland la
cunostintele elementare de Mecanica fluidelor,
si apeland la
cunostintele elementare de Mecanica fluidelor, ![]() . In acest context, (19.9) devine:
. In acest context, (19.9) devine:
![]() (19.10)
(19.10)
unde:
![]() momentul elementar al stabilitatii
de forma;
momentul elementar al stabilitatii
de forma;
![]() momentul elementar al stabilitatii
de greutate.
momentul elementar al stabilitatii
de greutate.
In
concluzie, momentul stabilitatii de forma este momentul
rezultant al actiunii fortelor verticale de presiune suplimentara
in raport cu o axa paralela cu axa ![]() ce trece prin
ce trece prin ![]() , iar momentul stabilitatii de greutate este
momentul in raport cu aceeasi axa al fortelor orizontale de
presiune suplimentara.
, iar momentul stabilitatii de greutate este
momentul in raport cu aceeasi axa al fortelor orizontale de
presiune suplimentara.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 6718
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved