| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
| Navigatie |
Momentul unitar al inclinarii transversale si momentul unitar de asieta
Folosind formula metacentrica a
stabilitatii se poate calcula valoarea momentului exterior, care actionand
static asupra navei ii produce o inclinare transversala cu ![]() . Acest moment se noteaza cu
. Acest moment se noteaza cu ![]() si poarta
numele de moment unitar al inclinarii
transversale.
si poarta
numele de moment unitar al inclinarii
transversale.
Cand
asupra unei nave actioneaza static un moment exterior producandu-i o
inclinare transversala in zona unghiurilor considerate mici, valoarea lui ![]() se determina din
ecuatia:
se determina din
ecuatia:
![]() (20.1)
(20.1)
Daca
in relatia (20.1) se face ![]() rezulta valoarea
lui
rezulta valoarea
lui ![]()
![]() (20.2)
(20.2)
Cunoscand
valoarea lui ![]() calculata cu
formula (20.2), la actiunea statica a unui moment exterior
calculata cu
formula (20.2), la actiunea statica a unui moment exterior ![]() ; nava se va inclina transversal cu unghiul
; nava se va inclina transversal cu unghiul ![]() masurat in grade:
masurat in grade:
![]() (20.3)
(20.3)
Folosind formula metacentrica a
stabilitatii longitudinale vom calcula valoarea momentului exterior
de inclinare, care actionand static asupra navei ii produce o variatie
de asieta de un centimetru. Acest moment se noteaza cu ![]() si se numeste
moment unitar de asieta.
si se numeste
moment unitar de asieta.
Diferenta de asieta a unei nave este:
![]() (20.4)
(20.4)
Acestei diferente de asieta ii corespunde un unghi de inclinare longitudinala
![]()
Cand
un moment exterior longitudinal ![]() actioneaza
static asupra navei conditia de stabilitate este:
actioneaza
static asupra navei conditia de stabilitate este:
![]() (20.5)
(20.5)
Daca
in formula (20.5) facem ![]() rezulta:
rezulta:
![]() (20.6)
(20.6)
Aceasta
marime are o larga utilitate practica in timpul exploatarii
navei permitand calculul diferentei de asieta ![]() masurata in
centimetri, atunci cand asupra navei actioneaza momentul exterior de
inclinare longitudinala cunoscut,
masurata in
centimetri, atunci cand asupra navei actioneaza momentul exterior de
inclinare longitudinala cunoscut, ![]() :
:
![]() (20.7)
(20.7)
Daca
![]() , adica nava se aproveaza, inclinarea longitudinala
se considera pozitiva.
, adica nava se aproveaza, inclinarea longitudinala
se considera pozitiva.
Forte perturbatoare
Marimea fortelor perturbatoare si a momentelor de inclinare care actioneaza in timpul exploatarii asupra navei, determina marimea momentului care va trebui generat de forta de greutate si forta de impingere, pentru a preveni rasturnarea navei sau aparitia inclinarilor exagerate. Fortele perturbatoare care afecteaza stabilitatea transversala au cauze externe si interne.
Ca exemple de cauze externe amintim:
a) Actiunea vantului simultan sau nu cu existenta miscarii de ruliu;
b) Ambarcarea de greutati cu ajutorul mijloacelor de la bord;
c) Giratia navei cu viteza mare;
d) Esuarea;
Dintre cauzele interne care afecteaza stabilitatea navei precizam:
e) Deplasarea de greutati la bord;
f) Ambarcarea de apa pe punte in timpul navigatiei datorita miscarilor pe care nava le executa pe mare agitata.
Aceste situatii vor fi tratate in lucrarea de fata; unele chiar in cadrul acestui capitol [b), e)] , altele in capitolele ulterioare [a), d)] .
Cand asupra navei actioneaza
un vant de la travers, presiunea acestuia va actiona pe proiectia
suprafetei emerse a corpului in ![]() ; denumita si suprafata velica.
Considerand presiunea constanta pe aceasta suprafata forta
rezultanta va actiona in centrul de greutate al suprafetei
velice imprimand navei o miscare de deriva. Ca o consecinta,
mediul marin va raspunde cu o forta egala si de sens
contrar care actioneaza pe suprafata imersa a navei, moment
in care miscarea de deriva se stabilizeaza (Fig. 58).
; denumita si suprafata velica.
Considerand presiunea constanta pe aceasta suprafata forta
rezultanta va actiona in centrul de greutate al suprafetei
velice imprimand navei o miscare de deriva. Ca o consecinta,
mediul marin va raspunde cu o forta egala si de sens
contrar care actioneaza pe suprafata imersa a navei, moment
in care miscarea de deriva se stabilizeaza (Fig. 58).
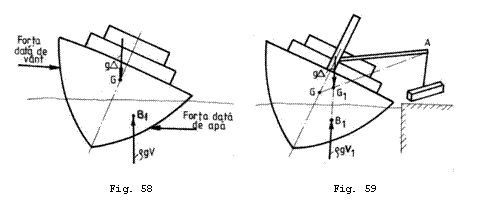
Cuplul fortelor exterioare va inclina nava transversal iar echilibrul se va realiza atunci cand sunt indeplinite urmatoarele doua conditii:
a) nava are o miscare de deriva cu viteza constanta ceea ce inseamna ca forta de presiune a vantului este egala cu forta de rezistenta a apei;
b) nava are o inclinare transversala
pana la unghi pentru care momentul cuplului fortelor exterioare este
egal cu momentul cuplului format de forta de greutate si forta
de impingere; forta care isi deplaseaza punctul de aplicatie
in ![]() .
.
Cand o greutate este ambarcata de
pe cheu cu ajutorul unei macarale de la bord, este ca si cand asupra navei
actioneaza vertical in jos, cu punctul de aplicatie in varful
macaralei (punctul ![]() din Fig. 59); o forta
egala cu greutatea ambarcata. Se demonstreaza usor folosind
cunostintele din Mecanica Teoretica faptul ca aceasta
situatie este similara cu deplasarea centrului de greutate din pozitia
din Fig. 59); o forta
egala cu greutatea ambarcata. Se demonstreaza usor folosind
cunostintele din Mecanica Teoretica faptul ca aceasta
situatie este similara cu deplasarea centrului de greutate din pozitia
![]() in pozitia
in pozitia ![]() situata pe
dreapta
situata pe
dreapta ![]() . Consecintele acestei ambarcari sunt urmatoarele:
. Consecintele acestei ambarcari sunt urmatoarele:
a) nava isi va mari pescajul pana cand surplusul de flotabilitate va egala greutatea ambarcata;
b) nava se va inclina transversal pana
cand centrul de carena se va deplasa in pozitia ![]() pe aceeasi
verticala cu noul centru de greutate
pe aceeasi
verticala cu noul centru de greutate ![]() .
.
Daca nava intra in miscare de giratie, apare o forta centrifuga care actioneaza in centrul de greutate al navei si este dispusa in plan orizontal. Aceasta forta este cu atat mai mare cu cat viteza navei este mai mare si raza de giratie este mai mica. Situatia este similara cu actiunea laterala a vantului asupra navei si este prezentata in Fig. 60.
Cand o nava esueaza (se
aseaza pe o stanca sau pe fundul senalului navigabil) o
parte din energia de deplasare va fi absorbita in timpul procesului de
ridicare pe verticala a navei, ceea ce inseamna aparitia unei
forte de reactiune ![]() in zona de contact.
Aceasta reactiune poate creste mai tarziu daca in zona
respectiva apare fenomenul de maree. In aceste conditii forta de
impingere va fi mai mica decat greutatea navei.
in zona de contact.
Aceasta reactiune poate creste mai tarziu daca in zona
respectiva apare fenomenul de maree. In aceste conditii forta de
impingere va fi mai mica decat greutatea navei.
Nava se va inclina si transversal pana cand momentul fortei de impingere fata de punctul de contact este egal cu momentul fortei de greutate fata de acelasi punct adica:
![]() (21.1)
(21.1)
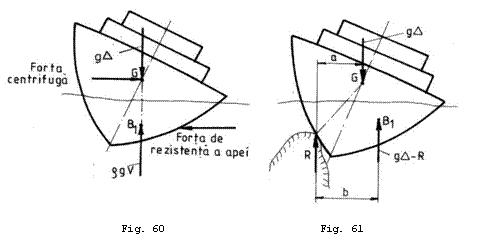
Cand reactiunea ![]() este mare, forta
de impingere se micsoreaza corespunzator si relatia
(21.1) nu mai poate fi satisfacuta, nava rasturnandu-se. Cazul esuarii
este prezentat in Fig. 61.
este mare, forta
de impingere se micsoreaza corespunzator si relatia
(21.1) nu mai poate fi satisfacuta, nava rasturnandu-se. Cazul esuarii
este prezentat in Fig. 61.
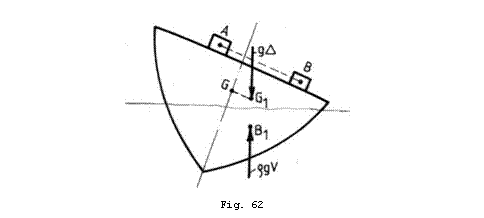
Daca la bordul unei nave are loc o
deplasare de greutati solide, lichide sau o deplasare pasagerilor la
bord; in aceeasi directie se va deplasa si centrul de greutate
al navei pana intr-un punct ![]() (Fig.62). Corespunzator,
nava se va inclina transversal pana cand centrul de carena ajunge
intr-o pozitie
(Fig.62). Corespunzator,
nava se va inclina transversal pana cand centrul de carena ajunge
intr-o pozitie ![]() situata pe aceeasi
verticala cu
situata pe aceeasi
verticala cu ![]() .
.
Pot aparea in timpul exploatarii navei si alte cazuri in care fortele perturbatoare determina inclinari ale navei. De exemplu fortele care se transmit prin cablul de remorca actioneaza si asupra navei remorcate si asupra remorcherului sau o nava ancorata se poate inclina datorita fortelor din lantul de ancora si al actiunii simultane a vantului. In toate cazurile inclinarea se va face pana la unghiul la care momentul de stabilitate egaleaza momentul de inclinare.
Este posibil de asemenea, ca fortele perturbatoare si implicit momentele de inclinare sa fie asa de mari incat echilibrul sa nu se poata realiza si nava sa se rastoarne.
Este de asemenea posibil ca echilibrul sa se realizeze la unghiuri mari de inclinare pentru care apa patrunde in interiorul navei prin deschiderile din puntea principala. Apa patrunsa se va acumula in bordul inclinat la partea inferioara a navei si poate cauza rasturnarea ei.
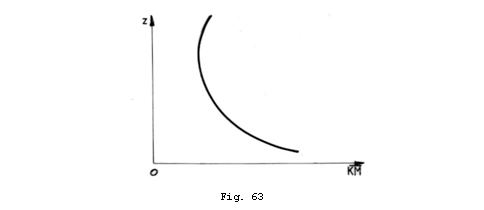
Variatia pozitiei metacentrului transversal cu pescajul.
Raza metacentrica diferentiala.
O variatie tipica a cotei metacentrului transversal
![]() (22.1)
(22.1)
cu
pescajul, este prezentata in Fig. 63. Se observa ca initial
![]() descreste rapid odata cu cresterea pescajului
pana la o valoare minima urmata de o crestere lenta.
Daca valoarea minima a lui
descreste rapid odata cu cresterea pescajului
pana la o valoare minima urmata de o crestere lenta.
Daca valoarea minima a lui ![]() corespunde unei situatii de serviciu a navei, atunci la
modificarea deplasamentului, prin ambarcarea sau debarcarea de greutati
la bord, cota metacentrului transversal va creste. O astfel de comportare
este favorabila stabilitatii navei, cu conditia ca
modificarea deplasamentului sa nu duca la marirea cotei
centrului de greutate
corespunde unei situatii de serviciu a navei, atunci la
modificarea deplasamentului, prin ambarcarea sau debarcarea de greutati
la bord, cota metacentrului transversal va creste. O astfel de comportare
este favorabila stabilitatii navei, cu conditia ca
modificarea deplasamentului sa nu duca la marirea cotei
centrului de greutate ![]() . Este evident ca natura curbei
. Este evident ca natura curbei ![]() depinde de natura derivatei
depinde de natura derivatei ![]() .
.
Tinand cont de (22.1) putem scrie:
![]() (22.2)
(22.2)
Pentru
un volum al carenei ![]() si o pozitie
initiala a centrului de carena
si o pozitie
initiala a centrului de carena ![]() , la o crestere infinitezimala a pescajului
, la o crestere infinitezimala a pescajului ![]() , volumul carenei va creste cu
, volumul carenei va creste cu ![]() si din ecuatia de momente scrisa fata
de un plan paralel cu planul de baza
si din ecuatia de momente scrisa fata
de un plan paralel cu planul de baza ![]() , ce trece prin centrul de carena initial, rezulta:
, ce trece prin centrul de carena initial, rezulta:
![]() (22.3)
(22.3)
Cunoscand
formula de calcul a razei metacentrice transversale (8.43) rezulta:
![]() (22.4)
(22.4)
sau mai departe:
![]() (22.5)
(22.5)
Inlocuind (22.5) si (22.3) in (22.2) rezulta:
![]() (22.6)
(22.6)
In
continuare vom incerca sa dam o interpretare termenului ![]() care apare in relatia (22.6).
care apare in relatia (22.6).
Se considera doua plutiri
drepte infinit apropiate ![]() si
si ![]() , precum si plutirile izocarene inclinate transversal cu
unghiul
, precum si plutirile izocarene inclinate transversal cu
unghiul ![]() ,
, ![]() si
si ![]() (Fig. 64). Prin
inclinare stratul de latime
(Fig. 64). Prin
inclinare stratul de latime ![]() si volum
si volum ![]() isi modifica
centrul de greutate trecand din
isi modifica
centrul de greutate trecand din ![]() in
in ![]() , avand in plan transversal o deplasare pe directia axei
, avand in plan transversal o deplasare pe directia axei
![]() egala cu
egala cu ![]() si una pe directia
axei
si una pe directia
axei ![]() egala cu
egala cu ![]() . Deplasari asemanatoare capata si
centrele de carena
. Deplasari asemanatoare capata si
centrele de carena ![]() si
si ![]() corespunzatoare
plutirilor
corespunzatoare
plutirilor ![]() si
si ![]() datorita inclinarilor
cu unghiul
datorita inclinarilor
cu unghiul ![]() . Notam cu
. Notam cu ![]() volumul carenei
corespunzatoare plutirii
volumul carenei
corespunzatoare plutirii ![]() .
.
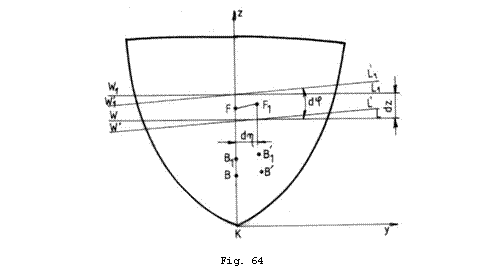
Daca vom
aplica teorema momentelor pentru volumul ![]() in raport cu planele
in raport cu planele ![]() si
si ![]() , dupa efectuarea catorva calcule elementare obtinem:
, dupa efectuarea catorva calcule elementare obtinem:
![]() (22.7)
(22.7)
Cand ![]() centrul de greutate al
volumului stratului de latime
centrul de greutate al
volumului stratului de latime ![]() se suprapune cu
centrul de greutate al plutirii
se suprapune cu
centrul de greutate al plutirii ![]() , marimile
, marimile ![]() si
si ![]() reprezentand variatiile
coordonatelor transversale ale acestuia. Daca nava se inclina
izocarenic in jurul tuturor axelor centrale, centrul plutirii se va deplasa pe
o suprafata denumita suprafata
centrelor de plutire. La o inclinare izocarenica in jurul axei
reprezentand variatiile
coordonatelor transversale ale acestuia. Daca nava se inclina
izocarenic in jurul tuturor axelor centrale, centrul plutirii se va deplasa pe
o suprafata denumita suprafata
centrelor de plutire. La o inclinare izocarenica in jurul axei ![]() , centrul plutirii se va deplasa pe o curba de pe aceasta
suprafata reprezentand curba
centrelor de plutire.
, centrul plutirii se va deplasa pe o curba de pe aceasta
suprafata reprezentand curba
centrelor de plutire.
La o inclinare izocarenica
transversala cu unghiul elementar ![]() (Fig. 65) centrul
plutirii se va deplasa din
(Fig. 65) centrul
plutirii se va deplasa din ![]() in
in ![]() parcurgand arcul
elementar
parcurgand arcul
elementar ![]() . Perpendiculara in
. Perpendiculara in ![]() pe
pe ![]() intersecteaza
planul diametral in punctul
intersecteaza
planul diametral in punctul ![]() . La limita
. La limita ![]()
![]() este centrul de curbura
al curbei centrelor de plutire iar distanta
este centrul de curbura
al curbei centrelor de plutire iar distanta ![]() se noteaza cu
se noteaza cu ![]() si reprezinta raza de curbura a acestei curbe.
si reprezinta raza de curbura a acestei curbe.
Lungimea arcului elementar ![]() se poate scrie:
se poate scrie:
![]()
si pe de alta parte
![]() (22.8)
(22.8)
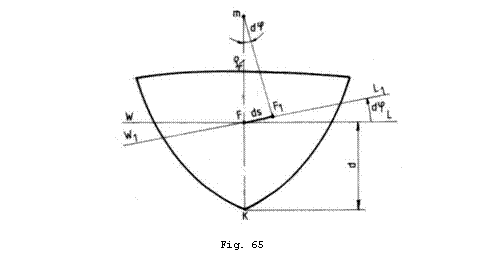
Rezulta:
![]() (22.9)
(22.9)
In
relatia (22.9) ![]() reprezinta un
infinit mic de ordinul doi care poate fi neglijat.
reprezinta un
infinit mic de ordinul doi care poate fi neglijat.
Ca atare (22.9) devine
![]() (22.10)
(22.10)
In final:
![]() (22.11)
(22.11)
Prin
analogie cu denumirile de metacentru si raza metacentrica
folosite anterior, ![]() se numeste
metacentru diferential, iar
se numeste
metacentru diferential, iar ![]() raza metacentrica
diferentiala. Introducem (22.11) in (22.6) si obtinem
pentru
raza metacentrica
diferentiala. Introducem (22.11) in (22.6) si obtinem
pentru ![]() :
:
![]() (22.12)
(22.12)
In
aceasta relatie ![]() este cota
metacentrului diferential. Putem avea urmatoarele trei situatii:
este cota
metacentrului diferential. Putem avea urmatoarele trei situatii:
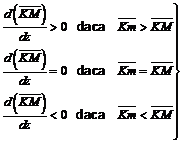 (22.13)
(22.13)
ceea
ce inseamna ca semnul derivatei ![]() depinde de pozitia
relativa a metacentrului diferential
depinde de pozitia
relativa a metacentrului diferential ![]() si a
metacentrului transversal
si a
metacentrului transversal ![]() .
.
Asa cum se observa din Fig.
66 raza metacentrica diferentiala poate fi negativa, caz in
care ![]() se gaseste
sub
se gaseste
sub ![]() .
.
Sa studiem in continuare factorii
de care depinde semnul razei metacentrice diferentiale ![]() . Inlocuim
. Inlocuim ![]() in formula (22.11)
in formula (22.11)
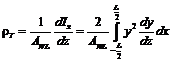
cunoscuta fiind relatia:
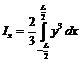 .
.
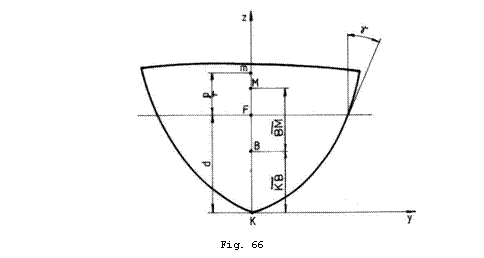
Cum
se observa din Fig. 66 ![]() . In consecinta:
. In consecinta:
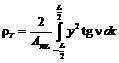 (22.14)
(22.14)
Daca
nava are bordurile evazate ![]() si
si ![]() . Daca nava are bordurile verticale in zona plutirii,
atunci
. Daca nava are bordurile verticale in zona plutirii,
atunci ![]() si
si ![]() ceea ce inseamna
ca metacentrul diferential
ceea ce inseamna
ca metacentrul diferential ![]() se gaseste
in planul plutirii. Era de asteptat un astfel de rezultat, deoarece la
navele cu borduri verticale pentru o inclinare infinit de mica
se gaseste
in planul plutirii. Era de asteptat un astfel de rezultat, deoarece la
navele cu borduri verticale pentru o inclinare infinit de mica ![]() ,
, ![]() ramane un punct
fix.
ramane un punct
fix.
In cazul unui ponton paralelipipedic cu
dimensiunile ![]() ;
; ![]() ,
, ![]() ,
, ![]() si ecuatia
si ecuatia ![]() devine:
devine:
![]() .
.
Rezolvand
aceasta ecuatie in raport cu necunoscuta ![]() gasim solutia
gasim solutia
![]() ceea ce inseamna
ca
ceea ce inseamna
ca ![]() depinde de valoarea
raportului
depinde de valoarea
raportului ![]() . Astfel cand:
. Astfel cand:
![]() si cota
metacentrului transversal scade;
si cota
metacentrului transversal scade;
![]() si cota
metacentrului transversal creste.
si cota
metacentrului transversal creste.
Pentru navele cu borduri evazate, tinand
cont de valoarea subunitara a coeficientilor de finete ![]() si
si ![]() , valoarea lui
, valoarea lui ![]() corespunzatoare
conditiei
corespunzatoare
conditiei ![]() este mai mare decat la
pontoanele paralelipipedice.
este mai mare decat la
pontoanele paralelipipedice.
23. Influenta salinitatii apei asupra stabilitatii si asietei navei
Asa cum am vazut in 12 pescajul mediu al navei variaza la trecerea din apa dulce in apa sarata si invers. In paragraful precedent am demonstrat ca variatia cotei metacentrului transversal cu pescajul se calculeaza cu relatia:
![]() (23.1)
(23.1)
La modificarea salinitatii apei deplasamentul ramane constant, volumul carenei modificandu-se:
![]() (23.2)
(23.2)
Daca diferentiem relatia (23.2)
![]() (23.3)
(23.3)
si
tinand cont ca pentru nave cu borduri verticale ![]() obtinem:
obtinem:
![]() (23.4)
(23.4)
Daca inlocuim (23.4) in (23.1) gasim:
![]() (23.5)
(23.5)
Asa
cum observam din (23.5), daca nava trece din apa dulce in apa
sarata ![]() si daca
metacentrul diferential
si daca
metacentrul diferential ![]() este situat deasupra
metacentrului transversal
este situat deasupra
metacentrului transversal ![]()
![]() , inaltimea metacentrica transversala se
micsoreaza si implicit stabilitatea. Daca metacentrul
diferential
, inaltimea metacentrica transversala se
micsoreaza si implicit stabilitatea. Daca metacentrul
diferential ![]() este pozitionat
sub metacentrul transversal
este pozitionat
sub metacentrul transversal ![]()
![]() , atunci inaltimea
metacentrica transversala se mareste si stabilitatea
deasemeni. Cand nava trece din apa sarata in apa dulce se
produc fenomenele inverse.
, atunci inaltimea
metacentrica transversala se mareste si stabilitatea
deasemeni. Cand nava trece din apa sarata in apa dulce se
produc fenomenele inverse.
In cazul navelor cu borduri verticale ![]() , relatia (23.5) devine:
, relatia (23.5) devine:
![]() (23.6)
(23.6)
Luand in discutie modificarea stabilitatii longitudinale atunci cand se schimba salinitatea apei se deduc formule similare cu (23.5) si (23.6):
![]() (23.7)
(23.7)
Avand
in vedere valorile mari ale razei metacentrice longitudinale, in paranteza de
mai sus se poate neglija diferenta ![]() si se obtine:
si se obtine:
![]() (23.8)
(23.8)
Cand nava trece din apa dulce in
apa sarata ![]() si inaltimea
metacentrica longitudinala creste. In situatia inversa
si inaltimea
metacentrica longitudinala creste. In situatia inversa
![]() ; ca urmare inaltimea metacentrica
longitudinala va scadea. In ambele cazuri, variatia inaltimii
metacentrice longitudinale nu va fi mai mare de
; ca urmare inaltimea metacentrica
longitudinala va scadea. In ambele cazuri, variatia inaltimii
metacentrice longitudinale nu va fi mai mare de ![]() % din valoarea initiala.
% din valoarea initiala.
Modificarea pescajului determina si
modificarea pozitiei centrului de carena al navei. Ne intereseaza
in mod special variatia abscisei centrului de carena ![]() .
.
Daca scriem ecuatia de momente statice fata de un plan paralel cu planul sectiunii de la mijlocul navei care trece prin centrul de carena initial, obtinem:
![]() (23.9)
(23.9)
Inlocuind
in relatia (23.9) variatia volumului carenei ![]() egala cu
egala cu
![]()
si
variatia pescajului la modificarea salinitatii apei ![]() cu
cu
![]()
obtinem
![]() (23.10)
(23.10)
Membrul drept al relatiei (23.10) poate fi considerat ca un moment exterior ce inclina nava in plan longitudinal, modificandu-i asieta. Acest moment este egalat de momentul de stabilitate longitudinala si obtinem:
![]() (23.11)
(23.11)
Rezulta unghiul de inclinare longitudinala
![]() (23.12)
(23.12)
care determina o variatie de asieta
![]() (23.13)
(23.13)
Cum pentru majoritatea navelor ![]() , cand nava trece din apa dulce in apa sarata
, cand nava trece din apa dulce in apa sarata
![]() nava se va apupa
nava se va apupa ![]() . In situatia inversa
. In situatia inversa ![]() si nava se va
aprova
si nava se va
aprova ![]() .
.
Pentru determinarea variatiilor de pescaj la extremitatile navei se utilizeaza relatiile:
![]() (23.14)
(23.14)
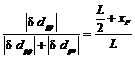 (23.15)
(23.15)
unde
![]() si
si ![]() sunt exprimate in
centimetri.
sunt exprimate in
centimetri.
Relatia (23.15) mai poate fi scrisa in forma:
![]() (23.16)
(23.16)
Pescajele finale se vor calcula cu formulele
![]() (23.17)
(23.17)
![]() (23.18)
(23.18)
Influenta deplasarilor de mase la bord asupra pozitiei si
stabilitatii navei
Sa consideram o nava, la
bordul careia o masa ![]() considerata in
categoria maselor mici
considerata in
categoria maselor mici ![]() se deplaseaza din
punctul
se deplaseaza din
punctul ![]() in punctul
in punctul ![]() . Aceasta deplasare nu va modifica deplasamentul navei
ci numai pozitia centrului de greutate si se poate descompune in trei
deplasari in lungul axelor de coordonate, asa cum se observa in
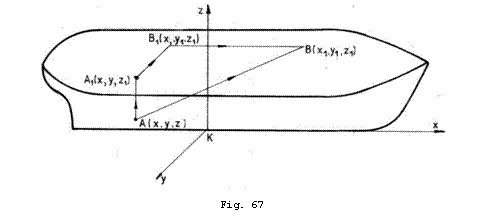
Fig.67.
. Aceasta deplasare nu va modifica deplasamentul navei
ci numai pozitia centrului de greutate si se poate descompune in trei
deplasari in lungul axelor de coordonate, asa cum se observa in
Fig.67.
- deplasare verticala din ![]() in
in ![]() pe distanta
pe distanta ![]() ;
;
- deplasare laterala ![]() in
in ![]() pe distanta
pe distanta ![]() ;
;
- deplasare longitudinala din ![]() in
in ![]() pe distanta
pe distanta ![]() .
.
Modificarea stabilitatii navei se identifica cu modificarea valorilor inaltimilor metacentrice transversala si longitudinala
![]() (24.1)
(24.1)
![]() (24.2)
(24.2)
In conditiile in care volumul
carenei ramane constant, pozitiile metacentrelor, transversal ![]() si longitudinal
si longitudinal ![]() , nu se schimba, prin urmare:
, nu se schimba, prin urmare:
![]() (24.3)
(24.3)
Pozitia pe inaltime a
centrului de greutate se modifica, datorita deplasarii pe directie
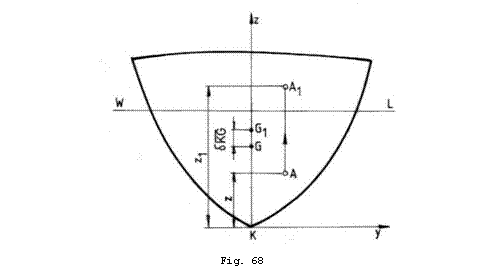
verticala a masei ![]() (Fig. 68), cu
cantitatea:
(Fig. 68), cu
cantitatea:
![]() (24.4)
(24.4)
Inlocuind (24.4) in (24.3) se obtine:
![]() (24.5)
(24.5)
Vom
observa ca daca masa ![]() se deplaseaza pe
verticala in jos
se deplaseaza pe
verticala in jos ![]() centrul de greutate se
va deplasa in acelasi sens si in consecinta stabilitatea se
va imbunatati
centrul de greutate se
va deplasa in acelasi sens si in consecinta stabilitatea se
va imbunatati ![]() . Cand masa
. Cand masa ![]() se deplaseaza pe verticala in sus, stabilitatea se
micsoreaza
se deplaseaza pe verticala in sus, stabilitatea se
micsoreaza ![]() .
.
Valorile inaltimilor metacentrice modificate se vor calcula cu formulele:
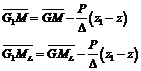 (24.6)
(24.6)
Daca nava are o inclinare initiala
![]() datorata actiunii
unui moment exterior, dupa deplasarea masei
datorata actiunii
unui moment exterior, dupa deplasarea masei ![]() pe verticala,
inclinarea se va modifica. Valoarea unghiului final de inclinare transversala
se determina din conditia:
pe verticala,
inclinarea se va modifica. Valoarea unghiului final de inclinare transversala
se determina din conditia:
![]() (24.7)
(24.7)
si rezulta:
![]() (24.8)
(24.8)
ceea ce inseamna ca inclinarea navei se va modifica proportional cu raportul inaltimilor metacentrice.
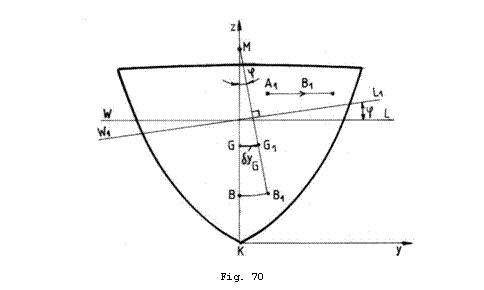
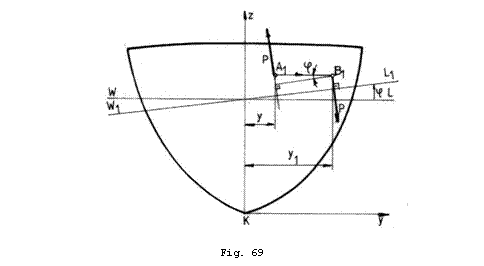
Deplasarea laterala a masei ![]() (Fig.69) din
(Fig.69) din ![]() in
in ![]() determina un
moment transversal de inclinare:
determina un
moment transversal de inclinare:
![]() (24.9)
(24.9)
Pentru
unghiuri mici de inclinare se poate considera ![]() si obtinem:
si obtinem:
![]() (24.10)
(24.10)
Momentul de stabilitate este:
![]() (24.11)
(24.11)
Din
egalitatea ![]() rezulta valoarea
unghiului de inclinare transversala
rezulta valoarea
unghiului de inclinare transversala
![]() (24.12)
(24.12)
La
acelasi rezultat se ajunge daca se apeleaza la urmatorul rationament.
Deplasarea laterala a masei ![]() pe distanta
pe distanta ![]() produce o deplasare pe
aceeasi directie a centrului de greutate al navei cu valoarea:
produce o deplasare pe
aceeasi directie a centrului de greutate al navei cu valoarea:
![]() (24.13)
(24.13)
asa
cum se observa din Fig. 70. Nava se va inclina transversal pana la
acel unghi ![]() pentru care
pentru care ![]() se afla pe aceeasi
verticala cu
se afla pe aceeasi
verticala cu ![]() si
si ![]() ; perpendiculara pe
; perpendiculara pe ![]() .
.
Deplasarea pe directie
longitudinala a masei ![]() pe distanta
pe distanta ![]() , modifica asieta navei (Fig. 71).
, modifica asieta navei (Fig. 71).
Daca rationam analog cu cazul inclinarii transversale, unghiul de inclinare longitudinala se calculeaza cu relatia:
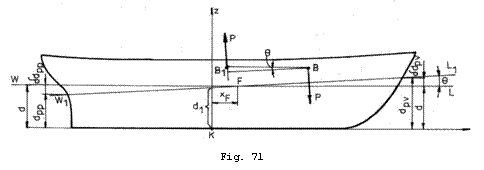
![]() (24.14)
(24.14)
Noua
plutire ![]() nu va mai fi dreapta
si va modifica pescajele la prova, la pupa, precum si la mijlocul
navei, dupa cum urmeaza:
nu va mai fi dreapta
si va modifica pescajele la prova, la pupa, precum si la mijlocul
navei, dupa cum urmeaza:
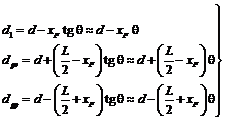 (24.15)
(24.15)
In
grupul de relatii (24.15) unghiul ![]() se masoara
in radiani, iar termenii
se masoara
in radiani, iar termenii
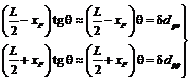 (24.16)
(24.16)
reprezinta
variatiile pescajelor la prova si la pupa. Unghiul ![]() se considera
pozitiv cand nava este aprovata si negativ cand este apupata.
se considera
pozitiv cand nava este aprovata si negativ cand este apupata.
Daca ![]() mase se deplaseaza
simultan la bordul navei, pentru a obtine efectul acestor deplasari
asupra pozitiei si stabilitatii navei, in algoritmul
prezentat mai sus se inlocuiesc:
mase se deplaseaza
simultan la bordul navei, pentru a obtine efectul acestor deplasari
asupra pozitiei si stabilitatii navei, in algoritmul
prezentat mai sus se inlocuiesc:
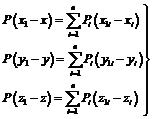 (24.17)
(24.17)
Putem, in finalul acestui paragraf, sa
prezentam un algoritm de calcul a efectelor pe care le produce, deplasarea
de mase ![]() la bord dintr-un punct
la bord dintr-un punct
![]() intr-un punct
intr-un punct ![]() . Se va proceda in urmatoarea succesiune:
. Se va proceda in urmatoarea succesiune:
a) se corecteaza inaltimile
metacentrice, transversala si longitudinala, cu aceeasi
valoare ![]() :
:
![]()
Intrucat
![]() se poate lucra cu inaltimea
metacentrica longitudinala necorectata,
se poate lucra cu inaltimea
metacentrica longitudinala necorectata, ![]() .
.
b) se calculeaza inclinarea transversala cu formula:
![]()
Daca
nava avea o inclinare transversala initiala ![]() , atunci inclinarea finala se va calcula cu formula:
, atunci inclinarea finala se va calcula cu formula:
![]()
c) se calculeaza unghiul de inclinare longitudinala cu relatia:
![]()
d) se calculeaza pescajele finale la extremitatile prova si pupa cu relatiile:
![]()
![]()
Daca nava nu era pe asieta
dreapta cu ![]() atunci noile pescaje
la extremitatile prova si pupa se calculeaza cu relatiile:
atunci noile pescaje
la extremitatile prova si pupa se calculeaza cu relatiile:
![]()
![]()
e) se calculeaza asieta finala (variatia pescajelor finale prova si pupa)
![]()
O valoare pozitiva a lui ![]() corespunde situatiei
de nava aprovata iar o valoare negativa situatiei de nava
apupata.
corespunde situatiei
de nava aprovata iar o valoare negativa situatiei de nava
apupata.
25. Proba de stabilitate
Inca din faza de proiectare a
navei, coordonatele centrului de greutate se determina prin calcul, luand
in considerare toate categoriile de greutati care compun
deplasamentul navei precum si repartizarea acestora pe nava. Datorita
complexitatii navei, a numarului foarte mare de elemente
componente, de forme si dimensiuni diferite, acest calcul in faza de
proiectare are un caracter aproximativ. De aceea, dupa terminarea constructiei
unei nave de tip nou sau dupa efectuarea de modificari importante in santier
si inainte de a se face probele de receptie, se verifica
deplasamentul si cota centrului de greutate de la planul de baza.
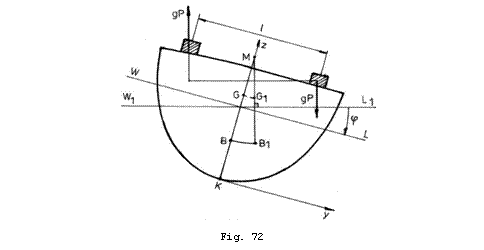
Verificarea se realizeaza prin efectuarea probei de stabilitate. Aceasta se bazeaza pe urmatorul rationament:
deplasarea unei mase ![]() dintr-un bord in
altul, in planul sectiunii transversale cu distanta
dintr-un bord in
altul, in planul sectiunii transversale cu distanta ![]() , va produce inclinarea navei cu unghiul
, va produce inclinarea navei cu unghiul ![]() , considerat in categoria unghiurilor mici (Fig. 72).
Deplasarea masei
, considerat in categoria unghiurilor mici (Fig. 72).
Deplasarea masei ![]() se face astfel incat
momentul de inclinare actioneaza static si pentru determinarea
unghiului de inclinare
se face astfel incat
momentul de inclinare actioneaza static si pentru determinarea
unghiului de inclinare ![]() se egaleaza
momentul de inclinare cu momentul de stabilitate. Momentul de inclinare este
dat de relatia:
se egaleaza
momentul de inclinare cu momentul de stabilitate. Momentul de inclinare este
dat de relatia:
![]() (25.1)
(25.1)
iar momentul de stabilitate se calculeaza cu formula metacentrica a stabilitatii:
![]() (25.2)
(25.2)
Egaland (25.1) cu (25.2) rezulta:
![]() (25.3)
(25.3)
si mai departe
![]() (25.4)
(25.4)
Daca se cunosc ![]() cota metacentrului
transversal fata de planul de baza
cota metacentrului
transversal fata de planul de baza ![]() si se determina
experimental unghiul de inclinare
si se determina
experimental unghiul de inclinare ![]() , se afla inaltimea centrului de greutate al
navei
, se afla inaltimea centrului de greutate al
navei![]() de la
de la ![]()
Proba de stabilitate se efectueaza cu deosebita atentie, mai ales ca rezultatele sunt folosite ca elemente de plecare pentru determinarea stabilitatii navei, in perioada ulterioara de exploatare. Lucrarile corespunzatoare probei de stabilitate cuprind trei etape distincte: pregatirea pentru proba, efectuarea probei si prelucrarea rezultatelor obtinute. Operatiunile pregatitoare pentru proba se fac in urmatoarea succesiune:
a) Se debarca toate sculele, materialele, instalatiile si dispozitivele folosite la efectuarea lucrarilor si se intocmeste tabelul cu toate masele care lipsesc de la bord fata de situatia de nava goala;
b) Se intocmeste tabelul cu toate masele in plus fata de situatia de proba;
c) Se pompeaza
in exterior toate masele lichide, iar tancurile rezervoare de lichide si
compartimentele corespunzatoare sunt golite si curatate;
d) Lichidele din instalatii se pastreaza la nivelul de serviciu, iar valvulele trebuiesc inchise;
e) Se instaleaza pendule pentru masurarea unghiurilor de inclinare. In mod obisnuit se instaleaza trei pendule; unul la prova, al doilea in zona de mijloc, iar al treilea in sectorul pupa, in planul diametral al navei. Pentru masurarea devierii pendulelor se instaleaza rigle gradate;
f) Se pregateste lestul
pentru proba de inclinare, determinandu-se masa necesara pentru efectuarea
probei. Se ambarca aceasta masa la bord stabilindu-se in acelasi
timp o dispunere cat mai rationala a acestuia la bord, astfel incat sa
nu se produca inclinarea longitudinala a navei; de obicei aceasta
masa se imparte in patru grupe, cate doua in fiecare bord. Masa
lestului nu trebuie sa produca o inclinare transversala mai mare
de ![]() ;
;
g) Proba de stabilitate se va efectua intr-un loc linistit, in lipsa valurilor, a vantului si a curentului. Toate scarile si schelele vor fi debarcate iar nava va fi legata cu cate o parama la prova si la pupa, astfel incat sa nu fie influentate inclinarile transversale ale navei. Echipajul va fi scos la mal, cu exceptia oamenilor care iau parte la efectuarea probei.
Efectuarea probei si prelucrarea rezultatelor se face respectand urmatoarea succesiune:
a) Inainte de inceperea probei se va face masuratoarea pescajului la scarile de pescaj din prova, cuplul maestru si pupa simultan in ambele borduri;
b) Pe baza pescajelor definitive,
utilizand diagrama de carene drepte se scot: deplasamentul ![]() , coordonatele centrului de carena
, coordonatele centrului de carena ![]() si
si ![]() ; razele metacentrice
; razele metacentrice ![]() si
si ![]() ;
;
c) Se deplaseaza lestul ![]() in directie
transversala cu distanta
in directie
transversala cu distanta ![]() , masurandu-se unghiul
, masurandu-se unghiul ![]() . Operatia se repeta de mai multe ori masurandu-se
unghiurile de inclinare si determinand inaltimea metacentrica
. Operatia se repeta de mai multe ori masurandu-se
unghiurile de inclinare si determinand inaltimea metacentrica
![]() cu relatia
(25.4). Pe de alta parte,
cu relatia
(25.4). Pe de alta parte, ![]() se poate calcula cu
relatia:
se poate calcula cu
relatia:
![]() (25.5)
(25.5)
de unde rezulta:
![]() (25.6)
(25.6)
Aceasta valoare a cotei centrului
de greutate va trebui corectata prin luarea in consideratie a maselor
in plus sau in minus iar cu ajutorul lui ![]() si al lui
si al lui ![]() se determina
abscisa centrului de greutate al navei cu formula:
se determina
abscisa centrului de greutate al navei cu formula:
![]() (25.7)
(25.7)
unde
![]() este unghiul de
inclinare longitudinala.
este unghiul de
inclinare longitudinala.
![]() (25.8)
(25.8)
26. Influenta incarcaturilor suspendate asupra stabilitatii navei
Printre tipurile de greutati ce compun deplasamentul navei la un moment dat, pot exista si greutati suspendate, care se vor deplasa liber prin inclinarea navei. Ca exemple putem da: o greutate suspendata in carligul macaralei sau o marfa suspendata in interiorul unei magazii, etc.
Pentru a determina efectul unor astfel
de sarcini asupra stabilitatii navei, vom considera o nava iar
in interiorul unei magazii o masa ![]() , suspendata in punctul
, suspendata in punctul ![]() prin intermediul unui
fir de lungime
prin intermediul unui
fir de lungime ![]() .
.
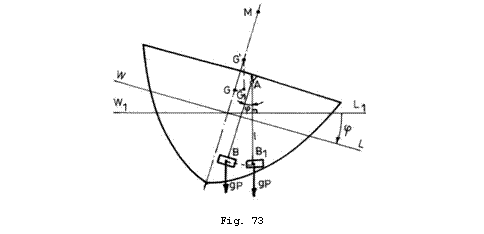
Cand nava este inclinata
transversal cu unghiul ![]() , masa
, masa ![]() isi deplaseaza
centrul de greutate din punctul
isi deplaseaza
centrul de greutate din punctul ![]() in
in ![]() parcurgand arcul de
cerc
parcurgand arcul de
cerc ![]() (Fig. 73), astfel
incat directia fortei de greutate sa fie in permanenta
verticala, perpendiculara pe suprafata apei. Unghiul de
inclinare transversala
(Fig. 73), astfel
incat directia fortei de greutate sa fie in permanenta
verticala, perpendiculara pe suprafata apei. Unghiul de
inclinare transversala ![]() este si unghiul
de rotatie al firului de lungime
este si unghiul
de rotatie al firului de lungime ![]() la capatul caruia
atarna masa
la capatul caruia
atarna masa ![]() .
.
In timpul inclinarii transversale
cu unghiul ![]() , deplasarea masei
, deplasarea masei ![]() determina un
moment exterior suplimentar de inclinare
determina un
moment exterior suplimentar de inclinare
![]() (26.1)
(26.1)
In aceste conditii momentul de stabilitate isi micsoreaza valoarea si devine:
![]() (26.2)
(26.2)
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4062
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved