| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
| Navigatie |
OSCILATIILE NAVEI
CONSIDERATII GENERALE
Prin oscilatie se intelege miscarea periodica executata de nava (considerata un corp rigid) aflata in stare de plutire pe mare calma sau agitata. In mod teoretic nava considerata un corp rigid poate executa sase miscari oscilatorii pe directia celor sase grade de libertate, trei rotatii si trei miscari liniare. Pe apa linistita nava oscileaza daca este scoasa din pozitia de echilibru de catre forte exterioare. Pe valuri nava oscileaza sub actiunea fortelor datorate maselor de apa aflate in miscare.
Pentru studiul oscilatiilor, se utilizeaza doua sisteme de coordonate (fig. 1):
un sisteme de coordonate fix Oξηζ, atasat suprafetei de plutire, avand originea pe verticala centrului de greutate a navei G;
un sistem de coordonate mobil Gxyz, atasat corpului navei aflat in miscare relativa fata de sistemul fix.
Axele sistemului mobil sunt axe centrale, principale de inertie.
Nava, considerata un solid rigid, liber, are sase grade de libertate, efectuand miscari pe toate cele trei directii:
1 deplasarea longitudinala (avansul);
2 deplasarea laterala (deriva);
3 deplasarea verticala;
4 rotatia in jurul axei x (ruliu);
5 rotatia in jurul axei y (tangaj);
6 rotatia in jurul axei z (pivotare).
Dupa directiile 1, 2 si 6, nava nu mai revine in pozitia initiala de echilibru, aceste miscari fiind obiectul studiului altor calitati ale navei.
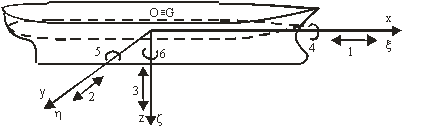
Fig. 1
De mare interes pentru comportarea navei si mai ales pentru consecinte il reprezinta urmatoarele tipuri de oscilatii:
Oscilatii transversale (ruliu) date de miscarea de rotatie periodica a navei in jurul axei longitudinale. Se prezinta sub forma unor deplasari unghiulare alternative, periodice, in planul cuplului maestru.
Oscilatii longitudinale (tangaj) date de miscarea de rotatie periodica a navei in jurul axei transversale. Reprezinta deplasari unghiulare alternative, periodice, in planul longitudinal al navei.
Oscilatii verticale date de deplasarea liniara periodica a navei in directie verticala in jurul pozitiei de echilibru.
Oscilatii cuplate rezultate din compunerea a cate doua sau trei oscilatii de tipuri diferite.
Pentru ca cele trei miscari periodice, necuplate, sa fie exprimate prin ecuatii diferentiale liniare se vor face urmatoarele ipoteze:
amplitudinile miscarilor sunt considerate mici, bordurile fiind verticale in limitele amplitudinilor, iar caracteristica de stabilitate corespunde stabilitatii initiale;
suprafata valului se considera plana, efectuand miscari periodice de translatie si de rotatie;
se neglijeaza efectul variatiei presiunii in val, in limita pescajului, datorita modificarii caracteristicilor valului cu adancimea.
Miscarile oscilatorii influenteaza negativ calitatile nautice ale navei, siguranta marfurilor la bord (miscarile produc deplasari, rostogoliri) si rezistenta structurii.
Aceste miscari dau nastere unor fenomene daunatoare cu consecinte mai mult sau mai putin grave pentru nava si incarcatura, cum sunt:
introducerea de forte si momente ale caror efecte pot provoca rasturnarea navei, ca urmare a pierderii stabilitatii;
aparitia fortelor de inertie si a loviturilor puternice de val, care pot duce la distrugerea partiala sau totala a navei;
micsorarea vitezei de mars a navei, deoarece bordurile, pupa si prova se afunda in apa (se mareste suprafata de frecare cu apa, rezultand cresterea rezistentei la inaintare);
inrautatirea conditiilor de viata la bordul navei, etc.
Miscarile oscilatorii, in special pe mare agitata, nu pot fi inlaturate, ci numai atenuate cu ajutorul unor instalatii speciale de amortizare a amplitudinii miscarilor. Data fiind influenta daunatoare a oscilatiilor, se iau o serie de masuri atat la proiectarea navelor cat si in timpul exploatarii lor in scopul micsorarii efectelor acestor oscilatii, astfel incat stabilitatea sa nu fie afectata.
Asupra caracterului miscarilor oscilatorii influenteaza in mare masura tipul navelor si modul de incarcare. Perioadele oscilatiilor depind de dimensiunile valurilor, dimensiunile principale ale navei, dispunerea incarcaturii la bord, viteza navei, drumul navei in raport cu directia valurilor, diferenta de faza dintre oscilatiile navei si oscilatiile valurilor, etc.
OSCILATIILE TRANSVERSALE SAU DE RULIU
Ruliul reprezinta miscarea de rotatie transversala a navei care are loc in jurul axului longitudinal care trece prin centrul de greutate. Este o oscilatie fortata produsa de fortele periodice exercitate de valuri si careia i se opun fortele de rezistenta ale mediului, de inertie si de redresare.
Studiul miscarii de ruliu prezinta interes practic atunci cand oscilatiile sunt provocate, intretinute si amplificate de hula. In cazul ruliului de hula, s-a constatat experimental ca perioada oscilatiilor este in general egala cu perioada oscilatiilor de ruliu in apa linistita, ceea ce justifica studierea initiala a ruliului in apa calma.
Studiul ruliului navei este necesar pentru a cunoaste eforturile la care este supus corpul navei datorita fortelor de inertie mari produse de miscarea oscilatorie si influenta lui asupra marfurilor incarcate.
Se alege ca sens pozitiv al unghiurilor de inclinare ![]() ale navei, al vitezelor unghiulare
ale navei, al vitezelor unghiulare ![]() si al acceleratiilor unghiulare
si al acceleratiilor unghiulare ![]() sensul orar, cand observatorul priveste de la
pupa spre prova.
sensul orar, cand observatorul priveste de la
pupa spre prova.
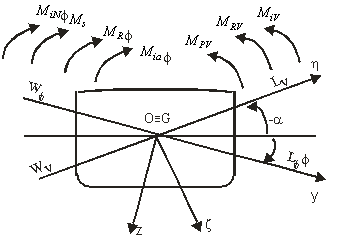
Fig.2
In cazul general, asupra navei vor actiona momentele (fig. 2):
![]() momentul fortelor de inertie al navei
momentul fortelor de inertie al navei
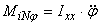 (1)
(1)
![]() momentul de stabilitate statica
momentul de stabilitate statica
![]() ; (2)
; (2)
![]() momentul fortelor de rezistenta ale apei
antrenata in miscare
momentul fortelor de rezistenta ale apei
antrenata in miscare
![]() (3)
(3)
![]() momentul fortelor de
inertie ale apei antrenata in miscare
momentul fortelor de
inertie ale apei antrenata in miscare
![]() (4)
(4)
![]() momentul perturbator dat de val.
momentul perturbator dat de val.
![]() (5)
(5)
![]() momentul fortelor de rezistenta suplimentar
din val
momentul fortelor de rezistenta suplimentar
din val
![]() (6)
(6)
![]() momentul fortelor de inertie suplimentar din
val
momentul fortelor de inertie suplimentar din
val
![]() (7)
(7)
Cunoscandu-se expresiile si sensurile celor sapte momente ce actioneaza asupra navei este usor sa se formuleze matematic miscarea, aplicand principiul lui D'Alembert si mai departe sa se determine caracteristicile mecanice influente din ecuatia diferentiala a miscarii:
![]() .
.
Daca se fac inlocuirile cu expresiile momentelor se obtine ecuatia diferentiala a miscarii de ruliu a navei pe valuri:
![]() (9)
(9)
unde
![]() este momentul de inertie al masei navei fata
de axa longitudinala
este momentul de inertie al masei navei fata
de axa longitudinala ![]() ;
;
![]() este momentul de inertie al masei de apa
antrenata in miscare fata de axa longitudinala
este momentul de inertie al masei de apa
antrenata in miscare fata de axa longitudinala ![]() ;
;
![]() este coeficient de amortizare.
este coeficient de amortizare.
Miscarea navei se studiaza atat in coordonate absolute pentru determinarea inclinarilor absolute, vitezelor si acceleratiilor fata de suprafata apei calme initiala, cat si in coordonate relative fata de suprafata valului, necesare pentru evaluarea gradului de inundare a puntii.
Studiul miscarii de ruliu, neamortizata pe apa linistita
Fortele care se iau in consideratie la studiul oscilatiilor libere al navei sunt:
deplasamentul navei;
forta de flotabilitate;
fortele de inertie ale apei si navei.
Deplasamentul navei ramane constant in timpul ruliului (incarcatura nu variaza), deci pozitia G a centrului de greutate al navei ramane neschimbata.
Forta de flotabilitate variaza ca pozitie, datorita faptului ca nava supusa miscarii de ruliu isi modifica volumul si forma operei vii, fata de plutirea dreapta. Se va schimba pozitia centrului de carena B, punct in care se aplica forta de flotabilitate.
Forta de flotabilitate si deplasamentul creeaza momentul de redresare al navei, moment ce se opune miscarii de ruliu, pe care o atenueaza treptat, imbunatatind astfel flotabilitatea navei.
Momentului de redresare ![]() in cazul miscarii de ruliu in apa calma,
pentru oscilatii mici executate de nava, este dat de relatia (2):
in cazul miscarii de ruliu in apa calma,
pentru oscilatii mici executate de nava, este dat de relatia (2):
![]()
Nava aflata in miscare de ruliu antreneaza o masa oarecare de apa, care
in virtutea principiului inertiei se va opune acestei miscari printr-un moment ![]() a carui expresie (4) este:
a carui expresie (4) este:
![]()
unde:
![]()
![]() este momentul de inertie masic al apei
antrenate, fata de axa
este momentul de inertie masic al apei
antrenate, fata de axa
longitudinala Gx a navei.
Valoarea momentului de inertie al apei antrenate de nava ![]() ,
depinde de forma si dimensiunile navei. Aceste momente se determina de obicei
pe cale experimentala.
,
depinde de forma si dimensiunile navei. Aceste momente se determina de obicei
pe cale experimentala.
In cazul miscarii de ruliu intervine si momentul de inertie al navei![]() ,
care se opune acestei miscari si a carui expresie (1) este:
,
care se opune acestei miscari si a carui expresie (1) este:
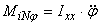
unde:
![]() este momentul de inertie masic al navei fata
de axa longitudinala Gx.
este momentul de inertie masic al navei fata
de axa longitudinala Gx.
Momentul de inertie ![]() nu trebuie confundat cu momentul de inertie al
suprafetei de plutire in raport cu axa longitudinala Gx a navei. Valoarea
momentului de inertie masic al navei se determina cu ajutorul unor formule
empirice, dintre care se foloseste in mod curent formula:
nu trebuie confundat cu momentul de inertie al
suprafetei de plutire in raport cu axa longitudinala Gx a navei. Valoarea
momentului de inertie masic al navei se determina cu ajutorul unor formule
empirice, dintre care se foloseste in mod curent formula:
![]() (10)
(10)
unde:
![]() - este raza de inertie [m];
- este raza de inertie [m];
![]() - deplasamentul navei in [kN];
- deplasamentul navei in [kN];
g - acceleratia gravitationala in [m/s2];
B = latimea navei la cuplu maestru in [m].
Raza de inertie a corpului navei fata de axa Gx se calculeaza cu relatia:
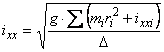 ,
(11)
,
(11)
unde:
![]() reprezinta masele componente de la bord;
reprezinta masele componente de la bord;
![]() este distanta de la axa de rotatie Gx la
centrul masei componente;
este distanta de la axa de rotatie Gx la
centrul masei componente;
![]() este momentul de inertie al masei i in raport cu axa proprie paralela cu
Gx.
este momentul de inertie al masei i in raport cu axa proprie paralela cu
Gx.
Din ecuatia (9) se obtine:
![]() (12)
(12)
Daca se imparte cu momentul de inertie masic, se obtine ecuatia diferentiala de ordinul doi, incompleta, omogena cu coeficienti constanti
![]() (13)
(13)
Daca notam
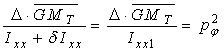 (14)
(14)
pulsatia oscilatiilor transversale libere, neamortizate, ecuatia (13) devine:
![]() (15)
(15)
a
carei ecuatie caracteristica este: ![]() ,
,
cu
radacinile imaginare: k1,2 =
i![]()
si solutia:
![]()
Constantele C1 si C2 se determina din conditiile initiale.
Astfel, in momentul initial, pentru t = 0, avem:
![]() si
si ![]() , adica:
, adica:
![]() din care rezulta
din care rezulta ![]() iar din
iar din
![]()
![]() rezulta
rezulta ![]()
Deci, ecuatia (12) se mai poate scrie, dupa inlocuire:
![]() , (17)
, (17)
sau sub forma armonica
![]() (18)
(18)
in care s-au notat:
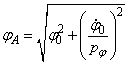 , amplitudinea
miscarii, (19)
, amplitudinea
miscarii, (19)
![]() (20)
(20)
faza initiala a oscilatiei libere neamortizata.
Ecuatia miscarii oscilatorii in cazul ruliului liber al navei
Amplitudinea
ruliului liber este teoretic constanta, fiind egala cu inclinarea initiala ![]() a navei fata de pozitia sa de echilibru
static.
a navei fata de pozitia sa de echilibru
static.
Pulsatia
unghiulara a oscilatiilor libere transversale este ![]() si are expresia:
si are expresia:
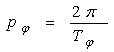 (21)
(21)
unde ![]() este perioada oscilatiilor libere de ruliu.
este perioada oscilatiilor libere de ruliu.
Din ecuatia (21) se obtine
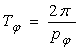 (22)
(22)
in care daca se inlocuieste relatia pulsatiei
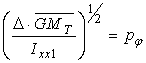 , se obtine urmatoarea expresie pentru calculul perioadei:
, se obtine urmatoarea expresie pentru calculul perioadei:
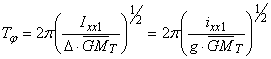 (23)
(23)
Perioada de ruliu ![]() depinde de valoarea
depinde de valoarea ![]() a
inaltimii metacentrice transversale. Daca aceasta inaltime este mare
(stabilitate buna), atunci
a
inaltimii metacentrice transversale. Daca aceasta inaltime este mare
(stabilitate buna), atunci ![]() va fi mica, iar oscilatiile au loc in mod
brusc (dure), si ca atare vitezele unghiulare vor atinge valori mai mari.
Depinzand si de
va fi mica, iar oscilatiile au loc in mod
brusc (dure), si ca atare vitezele unghiulare vor atinge valori mai mari.
Depinzand si de ![]() deci si de raza de inertie
deci si de raza de inertie ![]() ,
perioada de oscilatie poate creste la nave prin distribuirea corespunzatoare a
incarcaturii si echipamentelor diverse, si prin utilizarea chilelor de ruliu,
care maresc momentul de inertie al masei de apa..
,
perioada de oscilatie poate creste la nave prin distribuirea corespunzatoare a
incarcaturii si echipamentelor diverse, si prin utilizarea chilelor de ruliu,
care maresc momentul de inertie al masei de apa..
Practic, perioada proprie ![]() ,
se determina direct tinandu-se seama ca raza de inertie este proportionala cu
latimea navei folosind urmatoarea formula empirica:
,
se determina direct tinandu-se seama ca raza de inertie este proportionala cu
latimea navei folosind urmatoarea formula empirica:
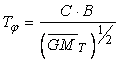 , (24)
, (24)
unde:
C - este coeficient de proportionalitate si reprezinta influenta distributiei greutatilor la bord si variaza intre 0,6 - 0,8 in raport de tipul navei;
B - latimea navei, in [m].
In baza formulei (24) a fost posibil sa se traseze curbele universale
de variatie ale inaltimii metacentrice ![]() in functie de perioada proprie si de latimea
navei.
in functie de perioada proprie si de latimea
navei.
Studiul miscarii de ruliu, cu amortizare pe apa linistita
In realitate amplitudinea ruliului nu este constanta, deoarece
oscilatiile se amortizeaza datorita rezistentei pe care o intampina corpul
navei din partea apei. Aceasta rezistenta este proportionala cu viteza
unghiulara ![]() de
inclinare a navei si se poate exprima printr-un moment
de
inclinare a navei si se poate exprima printr-un moment ![]() r care se opune miscarii de ruliu,
dat de relatia (3):
r care se opune miscarii de ruliu,
dat de relatia (3):
![]()
unde
![]() este coeficient de proportionalitate
(coeficient de amortizare).
este coeficient de proportionalitate
(coeficient de amortizare).
Coeficientul de amortizare datorat efectului apei in timpul oscilatiei transversale, se calculeaza cu metoda fasiilor. Astfel coeficientul de amortizare pe unitatea de lungime se determina cu relatia:
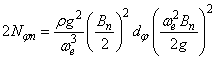 (25)
(25)
unde:
![]() este densitatea apei de mare;
este densitatea apei de mare;
![]() pulsatia de intalnire dintre nava si valuri;
pulsatia de intalnire dintre nava si valuri;
![]() latimea maxima a navei la sectiunea n;
latimea maxima a navei la sectiunea n;
![]() factor ce se determina grafic functie de
coeficientul de finete al suprafetei transversale si raportul
factor ce se determina grafic functie de
coeficientul de finete al suprafetei transversale si raportul![]() .
.
Pulsatia de intalnire dintre nava si valuri se determina cu relatia:
![]() (26)
(26)
unde
v este viteza de deplasare a navei;
c este viteza aparenta a valului;
![]() pulsatia absoluta a
valului;
pulsatia absoluta a
valului;
![]() unghiul de intalnire dintre directia de
propagare a valului si directia de deplasare a navei, masurat de la directia
valului in sensul acelor de ceas spre directia de deplasare a navei.
unghiul de intalnire dintre directia de
propagare a valului si directia de deplasare a navei, masurat de la directia
valului in sensul acelor de ceas spre directia de deplasare a navei.
Coeficientul total de amortizare, utilizand teoria fasiilor se determina din expresia:
![]() (27)
(27)
In acest caz ecuatia de echilibru a navei va fi:
![]() .
.
Inlocuind expresiile acestor momente se obtine ecuatia diferentiala a miscariii:
![]() (29)
(29)
iar
dupa impartire cu ![]()
![]() . (30)
. (30)
Se introduc notatiile (14) si
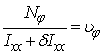 , (31)
, (31)
factorul de amortizare, astfel incat ecuatia (30) devine:
![]() (32)
(32)
Solutia ecuatiei (32) depinde de natura radacinilor ecuatiei sale caracteristice:
![]() . (33)
. (33)
Aceste radacini sunt:
![]()
dar
![]() ,
pentru ca
,
pentru ca ![]() ,
rezultand ca radacinile sunt complexe.
,
rezultand ca radacinile sunt complexe.
Daca se noteaza:
![]() (35)
(35)
pulsatia oscilatiei transversale amortizata, libera, radacinile ecuatiei (33) sunt:
![]() (36)
(36)
Solutia ecuatiei diferentiale (32) este:
![]() . (37)
. (37)
Constantele C1 si C2 se determina din conditiile
initiale. Astfel, in momentul initial cand t = 0 inclinarea ![]() si viteza unghiulara a navei aflata in miscare
de ruliu este
si viteza unghiulara a navei aflata in miscare
de ruliu este ![]() .
.
Din prima conditie rezulta ![]() .
.
Viteza unghiulara se obtine prin derivarea in raport cu timpul a expresiei (37).
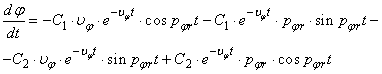 .
(38)
.
(38)
In momentul initial, avem:
![]()
de
unde rezulta 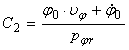
Introducand valorile lui C1 si C2 in relatia (37) se obtine:
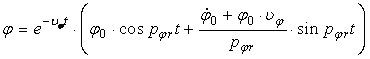
sau sub forma armonica
![]() (40)
(40)
In relatia (40) s-au notat expresiile:
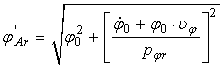
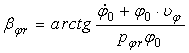 (42)
(42)
amplitudinea initiala a miscarii si faza initiala a oscilatiilor transversale amortizate pe apa linistita.
Legea de miscare de ruliu cu amortizare devine:
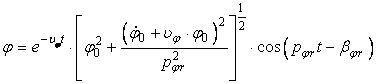 (43)
(43)
sau sub forma
![]()
unde: ![]() este amplitudinea oscilatiilor transversale
amortizate, libere, care descreste dupa o lege exponentiala in timp (fig. 3).
este amplitudinea oscilatiilor transversale
amortizate, libere, care descreste dupa o lege exponentiala in timp (fig. 3).
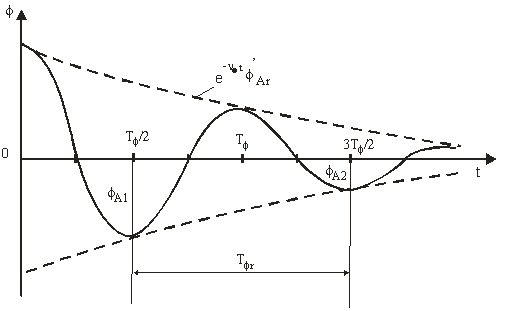
Fig.3
Din ecuatia (43) se observa ca miscarea de ruliu este o miscare
oscilatorie armonica amortizata, avand pulsatia ![]()
si
perioada 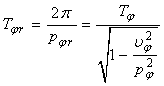 . (45)
. (45)
Tinand seama ca valoarea maxima a coeficientului de amortizare este:
![]()
se
poate remarca ca rezistenta mediului nu exercita o influenta esentiala asupra
perioadei proprii de ruliu a navei si ca pentru nevoile navigatiei ea poate fi
neglijata, cantitativ nedepasind erorile metodelor de determinare a perioadei ![]() ,
si
,
si ![]() .
.
Decrementul
logaritmic ![]() ,
ce reprezinta logaritmul natural al raportului dintre doua amplitudini
succesive, ne arata de cate ori amplitudinea descreste la o perioada de timp:
,
ce reprezinta logaritmul natural al raportului dintre doua amplitudini
succesive, ne arata de cate ori amplitudinea descreste la o perioada de timp:
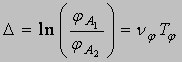 (46)
(46)
Daca se determina experimental decrementul logaritmic, utilizand
relatia (46), se poate calcula factorul de amortizare ![]()
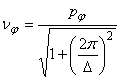 (47)
(47)
Timpul de amortizarea a oscilatiilor t, daca se adopta o valoare pentru raportul ![]() si se calculeaza
si se calculeaza 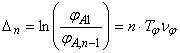 ,
se determina cu relatia:
,
se determina cu relatia:
![]() (48)
(48)
Oscilatia de ruliu pe valuri regulate in coordonate absolute
Se considera o nava pe valuri avand unghiul de intalnire ![]() .
.
La un moment dat t este definita pozitia relativa dintre nava si val:
![]() - inclinarea
relativa a navei - unghiul dintre axa Gz a navei si normala n la hula;
- inclinarea
relativa a navei - unghiul dintre axa Gz a navei si normala n la hula;
![]() - unghiul de
panta al hulei - care este egal cu unghiul de inclinare al normalei n cu verticala Oζ;
- unghiul de
panta al hulei - care este egal cu unghiul de inclinare al normalei n cu verticala Oζ;
![]() - inclinarea
absoluta a navei - unghiul dintre axele Gz si
Oζ.
- inclinarea
absoluta a navei - unghiul dintre axele Gz si
Oζ.
Inclinarea relativa este data de relatia
![]() (49)
(49)
In raport cu acest unghi se studiaza miscarea de ruliu relativa.
Suprafata libera a valului considerata simplu armonica, raportata la sistemul fix Oξηζ,
este data de ecuatia
![]() (50)
(50)
Daca
se considera ca originea sistemului fix se deplaseaza odata cu nava ![]() ,
ecuatia (50) devine:
,
ecuatia (50) devine:
![]() (51)
(51)
Panta hulei se obtine prin derivarea expresiei (50).in raport cu η:
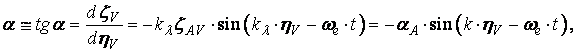
Facand aceeasi ipoteza ca la relatia (51), panta valului se determina cu expresia:
![]() (53)
(53)
S-au facut urmatoarele notatii:
![]() este pulsatia de intalnire (26);
este pulsatia de intalnire (26);
![]() , unde
, unde
![]() este amplitudinea valului regulat;
este amplitudinea valului regulat;
![]() este pulsatia formei valului;
este pulsatia formei valului;
![]() este lungimea valului.
este lungimea valului.
Derivatele pantei valului in raport cu timpul sunt date de relatiile:
![]() (54)
(54)
![]() (55)
(55)
Dupa inlocuirea expresiilor (53), (54) si (55) in (9) rezulta ecuatia:
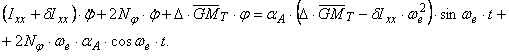
sau sub forma

in
care ![]() reprezinta diferenta de faza dintre momentul
perturbator si oscilatia unghiului de panta al valului
reprezinta diferenta de faza dintre momentul
perturbator si oscilatia unghiului de panta al valului
![]()
iar expresia
![]() (59)
(59)
reprezinta amplitudinea momentului perturbator.
Cu aceste notatii ecuatia (57) devine:
![]() (60)
(60)
Se imparte ecuatia cu ![]() si obtine forma
si obtine forma
![]() (61)
(61)
Daca se considera valul travers la nava si de amplitudine mica,
pulsatia de intalnire devine chiar pulsatia valului ![]() si termenii din ecuatia (56) care contin
si termenii din ecuatia (56) care contin ![]() si
si ![]() se neglijeaza, Se obtine ecuatia miscarii de
ruliu in forma simplificata
se neglijeaza, Se obtine ecuatia miscarii de
ruliu in forma simplificata
![]() (62)
(62)
sau sub forma
![]() .
(63)
.
(63)
Ecuatia (63) admite solutia ![]() ,
unde
,
unde ![]() este solutia ecuatiei omogene, iar
este solutia ecuatiei omogene, iar ![]() este solutia particulara.
este solutia particulara.
Consideram membrul doi egal cu zero si procedand ca in cazul ruliului in apa linistita, se obtine solutia de forma:
![]()
![]() (64)
(64)
Cand se tine cont si de membrul doi al relatiei (63) solutia
particulara ![]() este de forma:
este de forma:
![]() (65)
(65)
Punem conditia ca ![]() sa
verifice ecuatia (63) si se obtine.
sa
verifice ecuatia (63) si se obtine.
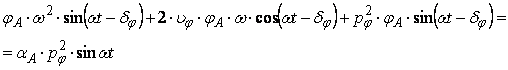
Solutia
particulara satisface ecuatia diferentiala pentru orice valori ![]() .
Se iau doua valori
.
Se iau doua valori ![]() si
si ![]() ,
obtinandu-se sistemul de ecuatii cu necunoscutele
,
obtinandu-se sistemul de ecuatii cu necunoscutele ![]() si
si ![]() :
:
![]()
![]() (68)
(68)
Ridicand la patrat cele doua ecuatii si adunandu-le rezulta expresia amplitudinii miscarii
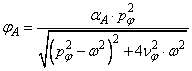 (69)
(69)
Din a doua ecuatie se obtine expresia defazajului dintre miscarea de oscilatie si excitatie
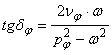 (70)
(70)
Daca se fac notatiile
: ![]() - coeficient de amortizare si
- coeficient de amortizare si
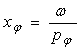 - pulsatia relativa a valului sau factor de
acordaj,
- pulsatia relativa a valului sau factor de
acordaj,
expresiile (69) si (70) devin:
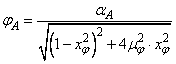 (69')
(69')
si 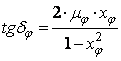 . . (70')
. Din expresiile legilor de miscare
(64) si (65) se poate observa ca oscilatia naturala are pulsatia de la miscarea
amortizata pe apa linistita si amplitudinea variabila dupa o lege exponentiala,
iar oscilatia fortata are pulsatia valului si amplitudinea constanta data de
relatia (69).
. . (70')
. Din expresiile legilor de miscare
(64) si (65) se poate observa ca oscilatia naturala are pulsatia de la miscarea
amortizata pe apa linistita si amplitudinea variabila dupa o lege exponentiala,
iar oscilatia fortata are pulsatia valului si amplitudinea constanta data de
relatia (69).
Deoarece oscilatia naturala se amortizeaza in timp, legea oscilatiei fortata stabilizata este:
![]() (71)
(71)
Pentru a analiza variatia amplitudinii oscilatiei stabilizate functie
de factorul de acordaj ![]() se
introduce notiunea de factor de amplificare
se
introduce notiunea de factor de amplificare ![]() dat de relatia
dat de relatia
 (72)
(72)
In activitatea practica, intereseaza in mod deosebit amplitudinea si
defazajul miscarii oscilatorii. In acest sens se vor reprezenta graficele de
variatie ale marimilor ![]() (fig. 4) si
(fig. 4) si ![]() (fig. 5)
(fig. 5)
a)
Pentru ![]() rezulta
rezulta ![]() .
Nava oscileaza pe un val cu lungime foarte mare, sau are un moment de inertie
foarte mic. In acest caz nava urmareste in permanenta suprafata valului, avand
inclinarea maxima egala cu amplitudinea unghiului de panta al valului.
.
Nava oscileaza pe un val cu lungime foarte mare, sau are un moment de inertie
foarte mic. In acest caz nava urmareste in permanenta suprafata valului, avand
inclinarea maxima egala cu amplitudinea unghiului de panta al valului.
b)
Pentru ![]() rezulta
rezulta ![]() .
Este cazul real de exploatare pe valuri cu perioade mici, sau nava are o
stabilitate foarte mica sau o inertie foarte mare.
.
Este cazul real de exploatare pe valuri cu perioade mici, sau nava are o
stabilitate foarte mica sau o inertie foarte mare.
c)
Pentru ![]() ,
cazul de rezonanta,
,
cazul de rezonanta, ![]() .
Factorul de amplificare depinde de coeficientul de amortizare al navei.
Amplitudinea oscilatiei este cu atat mai mare cu cat coeficientul de amortizare
este mai mic
.
Factorul de amplificare depinde de coeficientul de amortizare al navei.
Amplitudinea oscilatiei este cu atat mai mare cu cat coeficientul de amortizare
este mai mic
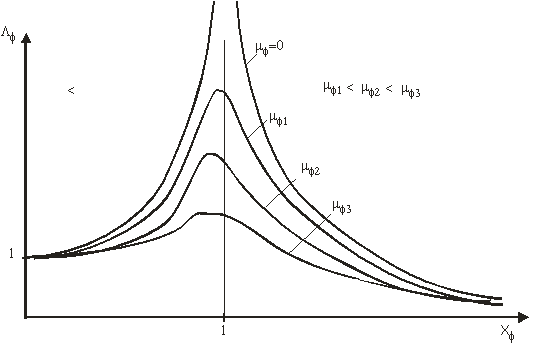
Fig. 4
Punctele de extem ale factorului de amplificare se obtin din egalarea
cu zero a primei derivate a functiei 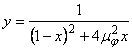 in raport cu x, introducandu-se notatiile
in raport cu x, introducandu-se notatiile ![]() si
si ![]() .
.
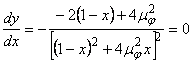 ,
,
din care rezulta
![]() si
si
![]() , sau daca se revine
la marimile initiale, considerand numai solutia pozitiva
, sau daca se revine
la marimile initiale, considerand numai solutia pozitiva
![]()
Din aceasta relatie se observa ca factorul de amplificare este maxim la valori mai mici decat 1, valoare ce corespunde rezonantei fara amortizare. Cunoscand pozitia de maxim, prin inlocuire in relatia (72) se obtine
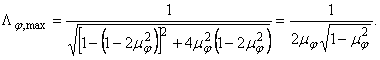 (74)
(74)
In figura 4 sunt reprezentate mai multe curbe de variatie a factorului de amplificare functie de factorul de racordaj, pentru diversi coeficienti de amortizare.Deoarece coeficientul de amortizare este foarte mic in comparatie cu unitatea, se considera ca pozitia si valoarea maxima a factorului de amplificare se afla in zona de rezonanta.
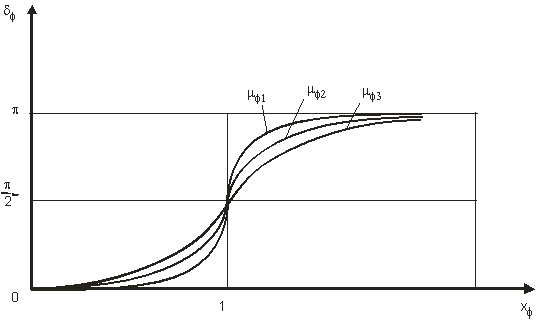
Fig. 5![]()
Din reprezentarea grafica a defazajului (fig. 5) se pot observa urmatoarele cazuri:
a)
Pentru![]() ,
,
![]()
![]() si
si ![]() .
Momentul perturbator este in faza cu unghiul de panta al valului;
.
Momentul perturbator este in faza cu unghiul de panta al valului;
b)
Pentru ![]()
![]()
![]() si
si ![]() ;
;
c)
Pentru ![]()
![]()
![]() si
si ![]() ;
;
d)
Pentru ![]()
![]()
![]() si
si ![]() .
.
Oscilatia transversala fortata in coordonate relative
Oscilatia transversala fortata in coordonate relative este dedusa din
ecuatia generala (9), folosind coordonata relativa ![]() si considerand valul travers la nava
si considerand valul travers la nava ![]() :
:
![]() (75)
(75)
Prin impartire cu momentul de inertei ![]() ,
se obtine o alta forma a ecuatiei (75), in care s-a folosit notatia
,
se obtine o alta forma a ecuatiei (75), in care s-a folosit notatia ![]() :
:
![]() (76)
(76)
Considerand ca oscilatia este amortizata, solutia are numai componenta particulara, caracteristica oscilatiei fortata stabilizata:
![]() (77)
(77)
in
care ![]() si
si ![]() reprezinta amplitudinea oscilatiei in
coordonate relative si
reprezinta amplitudinea oscilatiei in
coordonate relative si
defazajul , date de expresiile:
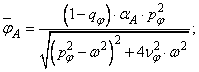 (78)
(78)
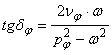
Daca se folosesc marimile adimensionale de la oscilatiile in coordonate
absolute, cu specificatia ca factorul de amplificare este ![]() ,
relatiile (78) si (79) devin:
,
relatiile (78) si (79) devin:
 ; (80)
; (80)
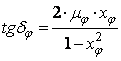 (81)
(81)
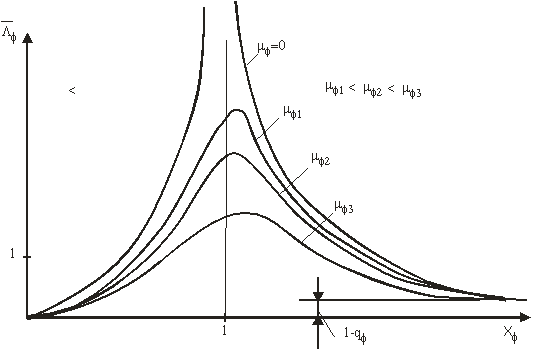
Fig. 6
Din anliza expresiei solutiei ecuatiei diferentiale in coordonate relative, se pot trage urmatoarele concluzii:
a)
Amplitudinea oscilatiei in coordonate relative ![]() este proportionala cu amplitudinea unghiului
de panta
este proportionala cu amplitudinea unghiului
de panta ![]() ;
;
b)
Amplitudinea oscilatiei in coordonate relative ![]() se poate micsora prin marirea momentului de
inertie a masei de apa antrenata in miscare care intervine in factorul
se poate micsora prin marirea momentului de
inertie a masei de apa antrenata in miscare care intervine in factorul ![]() ,
si prin cresterea coeficientului de amortizare
,
si prin cresterea coeficientului de amortizare ![]() ;
;
c)
Pentru ![]() rezulta
rezulta ![]() .
Nava oscileaza in faza cu valul. Aceasta este posibil in urmatoarele doua
situatii:
.
Nava oscileaza in faza cu valul. Aceasta este posibil in urmatoarele doua
situatii: ![]()
![]() respectiv
respectiv ![]() (val foarte lung);
(val foarte lung);
![]() respectiv
respectiv ![]() (stabilitate excesiv de mare);
(stabilitate excesiv de mare);
d)
Pentru ![]() rezulta
rezulta 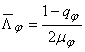 .
Apare fenomenul de rezonanta.Din relatie se poate observa ca coeficientul de
amortizare
.
Apare fenomenul de rezonanta.Din relatie se poate observa ca coeficientul de
amortizare ![]() influenteaza
valoarea maxima a amplitudinii. Aceasta influenta se stabileste studiind
extremitatile functiei (80).
influenteaza
valoarea maxima a amplitudinii. Aceasta influenta se stabileste studiind
extremitatile functiei (80).
Se procedeaza in mod asemanator ca la oscilatiile in coordonate absolute si se obtin pozitiile valorii maxime
![]() ;
; 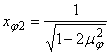 ,
(82)
,
(82)
si valoarea maxima a factorului de amplificare
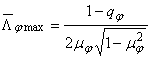 (83)
(83)
Din cele doua relatii si din graficul din figura 6 se poate vedea ca
valoarea maxima a factorului de amplificare scade cu cresterea coeficientului
de amortizare si se deplaseaza spre dreapta in raport cu ![]() .
.
e)
Pentru ![]() rezulta
rezulta
![]() .
Pentru pulsatii mari ale valului sau pulsatii proprii ale navei foarte mici,
nava tinde sa oscileze cu amplitudini apropiate de amplitudinea valului.
.
Pentru pulsatii mari ale valului sau pulsatii proprii ale navei foarte mici,
nava tinde sa oscileze cu amplitudini apropiate de amplitudinea valului.
In ceea ce priveste defazajul, discutia si graficul de variatie cu
factorul de acordaj ![]() sunt similare ca la oscilatia in coordonate
absolute (fig. 5).
sunt similare ca la oscilatia in coordonate
absolute (fig. 5).
OSCILATIILE LONGITUDINALE SAU DE TANGAJ
Miscarea de rotatie periodica a navei in jurul axei transversale Gy, sub actiunea momentelor exercitate de hula, se numeste oscilatie longitudinala ,sau de tangaj.
Pentru amplitudini mici, axa de rotatie in jurul caruia se produce miscarea se gaseste aproximativ la intersectia planului transversal care trece prin centrul de plutire si planul orizontal care trece prin centrul de greutate. In cazul miscarilor induse de valul de intalnire, oscilatia longitudinala nu poate fi separata de oscilatia verticala, datorita puternicelor interactiuni dintre acestea.
In baza ipotezelor adoptate in studiul oscilatiilor necuplate, se
considera ca asupra navei actioneaza un moment perturbator de forma armonica ![]() ,
care actioneaza in planul longitudinal al navei
,
care actioneaza in planul longitudinal al navei
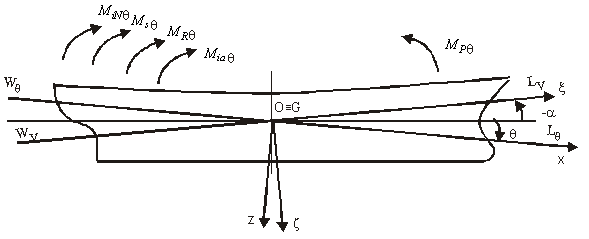
Fig. 7
Nava oscileaza sub actinea urmatoarelor momente(fig. 7):
![]() momentul fortelor de inertie al navei
momentul fortelor de inertie al navei
![]() (84)
(84)
![]() momentul de stabilitate statica
momentul de stabilitate statica
![]() ; (85)
; (85)
![]() momentul fortelor de rezistenta ale apei
antrenata in miscare
momentul fortelor de rezistenta ale apei
antrenata in miscare
![]() (86)
(86)
![]() momentul fortelor de inertie ale apei
antrenata in miscare
momentul fortelor de inertie ale apei
antrenata in miscare
![]() (87)
(87)
![]() momentul perturbator dat de val.
momentul perturbator dat de val.
![]() (88)
(88)
Cunoscandu-se expresiile si sensurile celor cinci momente ce actioneaza asupra navei este usor sa se formuleze matematic miscarea, aplicand principiul lui D'Alembert:
![]() .
.
Daca se fac inlocuirile cu expresiile momentelor se obtine ecuatia diferentiala a miscarii de tangaj a navei pe valuri:
![]() (90)
(90)
unde
![]() este momentul de inertie al masei navei fata
de axa transversala
este momentul de inertie al masei navei fata
de axa transversala ![]() ;
;
![]() este momentul de inertie al masei de apa
antrenata in miscare fata de axa transversala
este momentul de inertie al masei de apa
antrenata in miscare fata de axa transversala ![]() ;
;
![]() este coeficient de amortizare.
este coeficient de amortizare.
Miscarea navei se studiaza in coordonate absolute si se determina inclinarile absolute, vitezele si acceleratiile fata de suprafata apei calme initiala.
Studiul miscarilor de tangaj, neamortizate, pe apa linistita
Ecuatia diferentiala a miscarii este
![]() . (91)
. (91)
Momentul de inertie masic ![]() se
determina cu ajutorul unor formule empirice, dintre care se foloseste in mod
curent formula:
se
determina cu ajutorul unor formule empirice, dintre care se foloseste in mod
curent formula:
![]() (92)
(92)
unde:
![]() - este raza de
inertie [m] ( pentru nave cu forme normale
- este raza de
inertie [m] ( pentru nave cu forme normale
![]()
![]() - deplasamentul navei in [kN];
- deplasamentul navei in [kN];
g - acceleratia gravitationala in [m/s2];
Raza de inertie a corpului navei fata de axa Gy se calculeaza cu relatia:
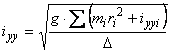 ,
(93)
,
(93)
unde:
![]() reprezinta masele componente de la bord;
reprezinta masele componente de la bord;
![]() este distanta de la axa de rotatie Gy lai
centrul masei componente;
este distanta de la axa de rotatie Gy lai
centrul masei componente;
![]() este momentul de inertie al masei i in raport cu axa proprie paralela cu
Gy.
este momentul de inertie al masei i in raport cu axa proprie paralela cu
Gy.
Momentul de inertie a masei de apa antrenata in miscare se calculeaza cu relatia
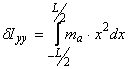 (94)
(94)
unde ![]() este
masa de apa specifica antrenata de nava, care se calculeza cu relatia
este
masa de apa specifica antrenata de nava, care se calculeza cu relatia
![]() (95)
(95)
in
care ![]() este densitatea apei, y semilatimea navei la linia de plutire in dreptul abscisei x si C coeficient, ce depinde de raportul
este densitatea apei, y semilatimea navei la linia de plutire in dreptul abscisei x si C coeficient, ce depinde de raportul ![]() si coeficientul de finete al sectiunii
transversale imerse.
si coeficientul de finete al sectiunii
transversale imerse.
Momentul de inetie al masei navei mai poate fi estimat cu relatia
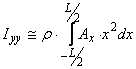 (96)
(96)
unde ![]() este aria sectiunii transversale imerse.
este aria sectiunii transversale imerse.
Din ecuatia (90) se obtine:
![]()
Daca se imparte cu momentul de inertie masic, se obtine ecuatia diferentiala de ordinul doi, incompleta, omogena cu coeficienti constanti:
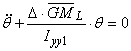 (98)
(98)
Se noteaza
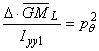 (99)
(99)
pulsatia oscilatiilor longitudinale libere, neamortizate, iar (98) devine:
![]() (100)
(100)
a
carei ecuatie caracteristica este ![]() ,
,
cu
radacinile imaginare: ![]()
si solutia ecuatiei diferentiala
![]() (101)
(101)
Constantele C1 si C2 se determina din conditiileinitiale.
Astfel, la momentul initial, pentru t = 0, se obtine:
![]() si
si ![]()
Dupa inlocuire in (101) se obtine expresia
![]() , (102)
, (102)
sau sub forma armonica
![]() (103)
(103)
in care s-au notat:
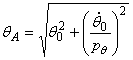 , amplitudinea
miscarii, si (104)
, amplitudinea
miscarii, si (104)
![]() (105)
(105)
faza initiala a oscilatiei libere neamortizata.
Perioada oscilatiilor libere de tangaj se calculeaza cu relatia:
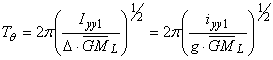 (106)
(106)
si depinde
de valoarea inaltimii metacentrice transversale ![]() .
Deoarece aceasta inaltime este mare (stabilitate buna), atunci perioada va fi
mica, iar oscilatiile vor fi dure, cu viteze unghiulare si acceleratii mai
mari.
.
Deoarece aceasta inaltime este mare (stabilitate buna), atunci perioada va fi
mica, iar oscilatiile vor fi dure, cu viteze unghiulare si acceleratii mai
mari.
Perioada oscilatiilor de tangaj ![]() se estimeaza cu relatia empirica:
se estimeaza cu relatia empirica:
![]()
unde T este pescajul navei corespunzator situatiei de incarcare.
Studiul miscarii de tangaj, amortizata pe apa linistita
Oscilatiile se amortizeaza datorita rezistentei pe care o intampina
corpul navei din partea apei. Aceasta rezistenta este proportionala in acest
caz de oscilatie cu viteza unghiulara ![]() de inclinare a navei, si se poate exprima
printr-un moment
de inclinare a navei, si se poate exprima
printr-un moment ![]() care se opune miscarii de tangaj, dat de
relatia (86):
care se opune miscarii de tangaj, dat de
relatia (86):
![]() (108)
(108)
unde
![]() este coeficient de proportionalitate
(coeficient de amortizare).
este coeficient de proportionalitate
(coeficient de amortizare).
Coeficientul de amortizare datorat efectului apei in timpul oscilatiei longitudinale, se calculeaza cu metoda fasiilor sau cu relatii empirice. Astfel coeficientul de amortizare se calculeaza cu formula lui Van-der-Fleet :
![]() ,
,
![]() (109)
(109)
unde:
![]() este momentul de inertie al suprafetei
plutirii, in raport cu axa transversala
este momentul de inertie al suprafetei
plutirii, in raport cu axa transversala ![]() ;
;
![]()
![]() este factor de proportionalitate care se
calculeaza cu relatia:
este factor de proportionalitate care se
calculeaza cu relatia:
![]() (110)
(110)
![]() este greutatea specifica a apei;
este greutatea specifica a apei;
M masa navei;
![]() coeficient adimensional
coeficient adimensional ![]() pentru amplitudini mici si
pentru amplitudini mici si ![]() pentru amplitudini mari.
pentru amplitudini mari.
In acest caz ecuatia de echilibru a navei va fi:
![]() .
.
Inlocuind expresiile acestor momente se obtine ecuatia diferentiala a miscariii:
![]()
iar
dupa impartire cu ![]() ,
,
![]() (113)
(113)
unde s-a notat factorul de amortizare 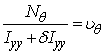 , (114)
, (114)
Din rezolvarea ecuatiei caracteristice corespunzatoare:
![]() (115)
(115)
rezulta radacinile:
![]() (116)
(116)
Daca se noteaza:
![]() (117)
(117)
pulsatia oscilatiei longitudinale amortizata, libera, radacinile ecuatiei (115) sunt:
![]() (118)
(118)
Solutia ecuatiei diferentiale (113) este:
![]() (119)
(119)
Constantele C1 si C2 se determina din conditiile initiale.
Astfel, in momentul initial cand t = 0 inclinarea ![]() si viteza unghiulara a navei aflata in miscare
de tangaj este
si viteza unghiulara a navei aflata in miscare
de tangaj este ![]() , obtinandu-se
, obtinandu-se ![]() si
si ![]()
Introducand valorile lui C1 si C2 in relatia (119) se obtine legea de miscare sub forma armonica:
![]() (120)
(120)
In relatia (120) s-au notat expresiile:
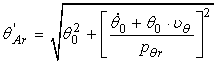 (121)
(121)
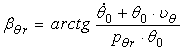
amplitudinea initiala a miscarii si faza initiala a oscilatiilor longitudinale amortizate pe apa linistita.
Legea de miscare de tangaj cu amortizare, devine:
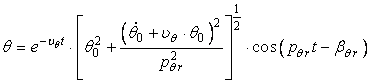 (123)
(123)
sau:
![]()
unde: ![]() este amplitudinea oscilatiilor longitudinale
amortizate, libere, care descreste dupa o lege exponentiala in timp (fig. 8).
este amplitudinea oscilatiilor longitudinale
amortizate, libere, care descreste dupa o lege exponentiala in timp (fig. 8).
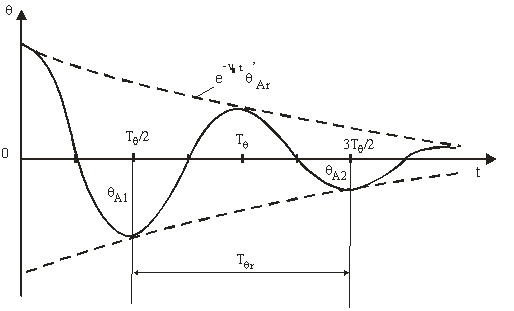
Fig.8
Din ecuatia (123) se observa ca miscarea de tangaj este in realitate o
miscare oscilatorie armonica amortizata, avand pulsatia ![]()
si
perioada 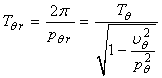 .
. ![]() (125)
(125)
Decrementul logaritmic ![]() ,
ce reprezinta logaritmul natural al raportului dintre doua amplitudini
succesive, este:
,
ce reprezinta logaritmul natural al raportului dintre doua amplitudini
succesive, este: 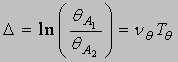
factorul de amortizare ![]() se calculeaza cu relatia
se calculeaza cu relatia
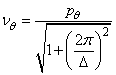 (126)
(126)
Timpul de amortizare a oscilatiilor t, se determina cu relatia:
![]() (127)
(127)
Oscilatia de tangaj pe valuri regulate in coordonate absolute
Ecuatia miscarii de ruliu in forma simplificata, in coordonate absolute este
![]()
sau sub forma
![]() .
(129)
.
(129)
Solutia particulara este de forma:
![]()
Punem conditia ca sa verifice ecuatia (129) si se obtine.
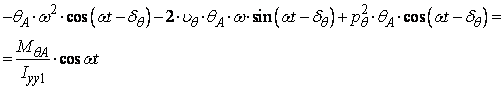
Solutia
particulara satisface ecuatia diferentiala pentru orice valori ![]() .
Se iau doua valori
.
Se iau doua valori ![]() si
si ![]() ,
obtinandu-se sistemul de ecuatii:
,
obtinandu-se sistemul de ecuatii:
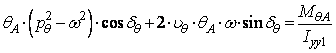 (132)
(132)
![]() (133)
(133)
Ridicand la patrat cele doua ecuatii si adunandu-le rezulta expresia amplitudinii miscarii
 (134)
(134)
Din a doua ecuatie se obtine expresia defazajului dintre miscarea de oscilatie si excitatie
![]() (135)
(135)
Daca se fac notatiile
: ![]() - coeficient de amortizare adimensional
si
- coeficient de amortizare adimensional
si
![]() - pulsatia relativa a valului sau factor de
acordaj,
- pulsatia relativa a valului sau factor de
acordaj,
expresiile (134) si (135) devin:

si 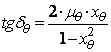 , . (135') unde
, . (135') unde ![]() reprezinta unghiul de inclinare sub actiunea
statica a amplitudinii momentului perturbator, iar .
reprezinta unghiul de inclinare sub actiunea
statica a amplitudinii momentului perturbator, iar . 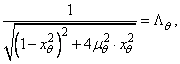 este factorul de amplificare
este factorul de amplificare
In activitatea practica, intereseaza in mod deosebit amplitudinea si
defazajul miscariioscilatorii. In acest sens se vor reprezenta graficele de
variatie ale marimilor ![]() (fig. 9) si
(fig. 9) si ![]() (fig. 10).
(fig. 10).
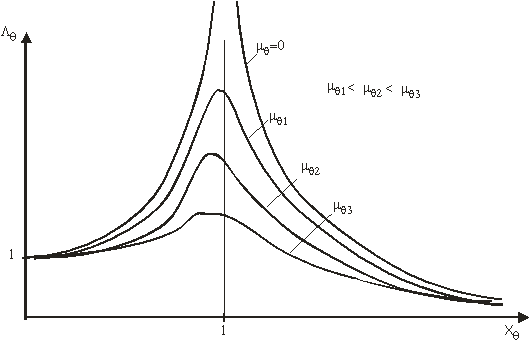
Fig.9
a)
Pentru ![]() rezulta
rezulta ![]() .
Nava oscileaza pe un val cu lungime foarte mare sau are un moment de inertie
foarte mic. In acest caz nava urmareste in permanenta suprafata valului, avand
inclinarea maxima egala cu amplitudinea unghiului de panta al valului.
.
Nava oscileaza pe un val cu lungime foarte mare sau are un moment de inertie
foarte mic. In acest caz nava urmareste in permanenta suprafata valului, avand
inclinarea maxima egala cu amplitudinea unghiului de panta al valului.
b)
Pentru ![]() rezulta
rezulta ![]() .
Este cazul real de exploatare pe valuri cu perioade mici sau are o inertie
foarte mare.
.
Este cazul real de exploatare pe valuri cu perioade mici sau are o inertie
foarte mare.
c)
Pentru ![]() ,
cazul de rezonanta,
,
cazul de rezonanta, ![]() .
La rezonanta factorul de amplificare depinde de coeficientul de amortizare al
navei. Amplitudinea oscilatiei este cu atat mai mare cu cat coeficientul de
amortizare este mai mic
.
La rezonanta factorul de amplificare depinde de coeficientul de amortizare al
navei. Amplitudinea oscilatiei este cu atat mai mare cu cat coeficientul de
amortizare este mai mic
Punctele de extem ale factorului de amplificare se obtin din egalarea
cu zero a primei derivate a functiei 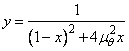 in raport cu x, introducandu-se notatiile
in raport cu x, introducandu-se notatiile ![]() si
si ![]() .
.
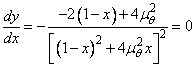
din care rezulta
![]() (136)
(136)
Din aceasta relatie se observa ca factorul de amplificare este maxim la valori mai mici decat 1, valoare ce corespunde rezonantei fara amortizare (Fig. ). Cunoscand pozitia de maxim prin inlocuire in relatia (134')
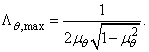
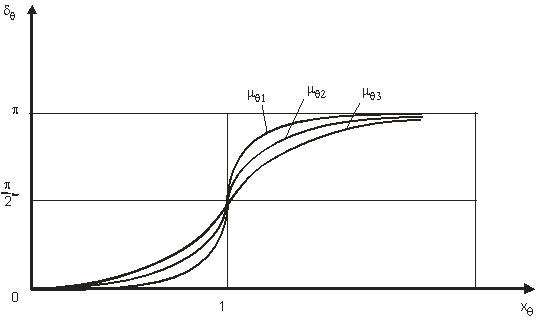
Fig. 10
Din reprezentarea grafica a defazajului (fig. 10) se pot observa urmatoarele cazuri:
a)
Pentru![]() ,
,
![]()
![]() .
Momentul perturbator este in faza cu unghiul de panta al valului;
.
Momentul perturbator este in faza cu unghiul de panta al valului;
b)
Pentru ![]()
![]()
![]() ;
;
c)
Pentru ![]()
![]()
![]() ;
;
d)
Pentru ![]()
![]()
![]() .
.
Studiul tangajului pe hula este asemanator cu cel al ruliului. Consideram cazul cand nava intra cu prova in val, iar lungimea hulei este de doua ori mai mare decat lungimea navei.
La tangajul pe mare agitata prezinta interes oscilatiile fortate,
deoarece oscilatiile libere se amortizeaza rapid datorita rezistentei mari
opusa de masa de apa antrenata. Axa de oscilatie la tangaj nu coincide, de
regula, cu axa transversala ![]() .
Pozitia axei de tangaj depinde de formele navei. Daca nava are o pupa lata si
plata, axa de tangaj se va gasi mai spre pupa si invers.
.
Pozitia axei de tangaj depinde de formele navei. Daca nava are o pupa lata si
plata, axa de tangaj se va gasi mai spre pupa si invers.
Deplasarea axei de tangaj de-a lungul navei se explica prin faptul ca rezistenta apei este diferita din cauza formelor diferite ale navei la prova si pupa. Dar de obicei, in urma tangajului, pupa se afunda mai mult fiind avantajos din punct de vedere al functionarii elicei.
Cand lungimea navei este mare in raport cu lungimea hulei oscilatiile miscarii de tangaj pot fi mari, viteza relativa a navei in raport cu hula fiind astfel importanta.
Daca nava merge cu valuri din prova si cu viteza mare, tangajul va creste. Nava inainteaza in acest caz mai incet, cu variatii bruste de viteza. Daca nava este mult iesita din apa, scade periculos stabilitatea transversala, iar cand se afunda se pot produce socuri violente ce pot provoca avarii serioase corpului navei si incarcaturii din nava.
Daca nava merge cu valuri din pupa, efectele de mai sus sunt atenuate, insa pozitia relativa a navei in raport cu hula variaza mai incet.
Cand viteza v a navei este egala cu viteza c a hulei, nava ramane mult timp in aceeasi pozitie fata de hula, situatie periculoasa privind stabilitatea transversala si guvernarea navei.
Cand nava se gaseste pe doua creste de val, este un caz destul de periculos deoarece apar eforturi mari ce actioneaza asupra corpului navei si care solicita excesiv materialul.
OSCILATIA VERTICALA A NAVEI
Oscilatia pe verticala este o miscare periodica de translatie pe verticala a navei considerata corp rigid, sub actiunea fortelor hidrostatice, hidrodinamice din hula si a fortei de inertie a navei.
Consideram o nava pe plutire dreapta (fig. 11) asupra careia actioneaza
o forta verticala orientata de sus in jos. Sub actiunea acestei forte creste pescajul
navei cu ![]() ,
linia de plutire devine
,
linia de plutire devine ![]() si este paralela cu plutirea initiala. Si in
acest caz raman valabile ipotezele admise la studiul miscarilor de ruliu si
tangaj
si este paralela cu plutirea initiala. Si in
acest caz raman valabile ipotezele admise la studiul miscarilor de ruliu si
tangaj
Daca aceasta forta inceteaza atunci nava incepe sa execute oscilatii verticale, de o parte si de alta a liniei de plutire initiala WL.
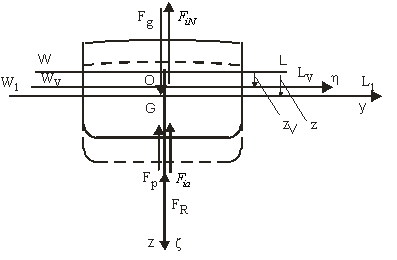
Fig. 11
Asupra navei, in timpul oscilatiilor, actioneaza urmatoarele forte:
Forta de greutate, aplicata in centrul de greutate G
![]() (138)
(138)
Forta de flotabilitate, aplicata in centrul de carena B
![]() (3.139)
(3.139)
Forta de inertie care actioneaza asupra masei navei, care se aplica in centrul de greutate G
![]() (140)
(140)
Forta de inertie a masei de apa antrenata,
![]() (141)
(141)
Forta de rezistenta a apei, proportionala cu viteza relativa de afundare.
![]() (142)
(142)
S-a notat cu ![]() coeficientul de proportionalitate, M masa navei,
coeficientul de proportionalitate, M masa navei, ![]() masa apei antrenata in miscare
masa apei antrenata in miscare
Scriind ecuatia echilibrului dinamic al fortelor ce actioneaza asupra navei aflata in miscare oscilatorie verticala, se obtine:
![]() (143)
(143)
sau daca se separa variabilele
![]() (144)
(144)
Miscarea navei se studiaza atat in coordonate absolute (144) pentru determinarea deplasarilor, vitezelor si acceleratiilor absolute fata de suprafata apei calme initiala, cat si in coordonate relative fata de suprafata valului.
Daca in ecuatia (143) se noteaza ![]() ,
,
![]() si
si ![]() acceleratia, viteza si deplasarea relative, se
obtine:
acceleratia, viteza si deplasarea relative, se
obtine:
![]()
Ecuatia valului raportat la sistemul Gxyz este de forma:
![]() (146)
(146)
iar primele doua derivate in raport cu timpul sunt:
![]() (147)
(147)
![]() (148)
(148)
unde ![]() este amplitudinea valului, iar
este amplitudinea valului, iar ![]() frecventa de intalnire a valului.
frecventa de intalnire a valului.
Daca se inlocuiesc relatiile (146), (147) si (148) in (144) si (145) se obtine:
![]()
si ![]() (145')
(145')
Aceste doua ecuatii diferentiale ale oscilatiei verticale, in coordonate absolute si relative se scriu in final sub forma:
![]() , (149)
, (149)
![]()
unde:
![]() , este amplitudinea
fortei
, este amplitudinea
fortei
perturbatoare la oscilatiile in coordonate
![]() , este amplitudinea
fortei perturbatoare, la oscilatiile in coordonate
, este amplitudinea
fortei perturbatoare, la oscilatiile in coordonate
![]() este amplitudinea valului;
este amplitudinea valului;
![]() , reprezinta
defazajul dintre forta perturbatoare si miscarea valului.
, reprezinta
defazajul dintre forta perturbatoare si miscarea valului.
Studiul oscilatiilor verticale, neamortizate pe apa linistita
In baza ipotezei facute, ca deplasarile pe verticala sunt mici, termenii
din membrul doi ai ecuatiei (144) ce contin pe ![]() si
si ![]() se neglijeaza si se obtine ecuatia de miscare
in forma simplificata
se neglijeaza si se obtine ecuatia de miscare
in forma simplificata
![]() . (151)
. (151)
Din ecuatia (151) se obtine:
![]()
Daca se imparte cu ![]() ,
se obtine ecuatia diferentiala de ordinul doi, incompleta, omogena cu
coeficienti constanti
,
se obtine ecuatia diferentiala de ordinul doi, incompleta, omogena cu
coeficienti constanti
![]()
Daca se noteaza 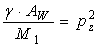 (154)
(154)
pulsatia oscilatiilor verticale libere, neamortizate, ecuatia (153) devine:
![]() (155)
(155)
a
carei ecuatie caracteristica este: ![]() ,
,
cu
radacinile imaginare: k1,2 =
i![]()
si solutia:
![]()
Constantele C1 si C2 se determina din conditiile initiale.
Astfel, in momentul initial, pentru t = 0, avem:
![]() si
si ![]() , din care rezulta
, din care rezulta ![]() si
si ![]()
Solutia (156) se mai poate scrie, dupa inlocuire:
![]() , (157)
, (157)
sau sub forma armonica
![]()
in care s-au notat:
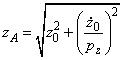 , amplitudinea
miscarii, (159)
, amplitudinea
miscarii, (159)
![]()
faza initiala a oscilatiei libere neamortizata.
Masa apei antrenata in miscare se poate calcula cu
formule empirice, aproximative:. 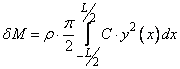 , (161)
, (161)
unde y
este semilatimea la plutirea navei in sectiunea x, C este coeficient pentru
sectiunile Lewis, determinat grafic functie de raportul ![]() ,
coeficientul de finete al sectiunii transversale si functie de frecventa de
intalnire a valului, prin expresia
,
coeficientul de finete al sectiunii transversale si functie de frecventa de
intalnire a valului, prin expresia ![]()
Pulsatia
oscilatiilor libere verticale este ![]() si are expresia:
si are expresia:
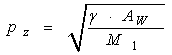
Pentru determinarea pulsatiei se utilizeaza si formule aproximative:
![]() (162)
(162)
unde ![]() este coeficientul de finete al suprafetei de
plutire.
este coeficientul de finete al suprafetei de
plutire.
Perioada oscilatiilor verticale este:.
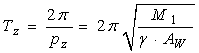 (163)
(163)
Perioada oscilatiei verticale ![]() depinde de valoarea
depinde de valoarea ![]() a masei navei si apei antrenata in miscare si
invers proportional de aria suprafetei de plutire. Practic, perioada proprie
a masei navei si apei antrenata in miscare si
invers proportional de aria suprafetei de plutire. Practic, perioada proprie ![]() se determina direct folosind formula empirica:
se determina direct folosind formula empirica:
![]() , (164)
, (164)
unde
factorul ![]() este dat de expresia
este dat de expresia
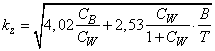
iar ![]() este coeficientul bloc.
este coeficientul bloc.
Studiul oscilatiilor verticale, cu amortizare pe apa linistita
Amplitudinea oscilatiei verticale nu este constanta, deoarece
oscilatiile se amortizeaza datorita rezistentei pe care o intampina corpul
navei din partea apei. Aceasta rezistenta este proportionala cu viteza liniara ![]() de
oscilatie a navei, si se poate exprima prin relatia:
de
oscilatie a navei, si se poate exprima prin relatia:
![]()
unde
![]() este coeficient de proportionalitate
(coeficient de amortizare).
este coeficient de proportionalitate
(coeficient de amortizare).
Coeficientul de amortizare datorat efectului apei in timpul oscilatiei verticale, se calculeaza cu metoda fasiilor. Astfel, coeficientul de amortizare pe unitatea de lungime se determina cu relatia:
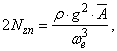 (167)
(167)
unde:
![]() este densitatea apei de mare;
este densitatea apei de mare;
![]() pulsatia de intalnire dintre nava si valuri;
pulsatia de intalnire dintre nava si valuri;
![]() factor ce se determina grafic functie de
coeficientul de finete al suprafetei transversale, raportul
factor ce se determina grafic functie de
coeficientul de finete al suprafetei transversale, raportul![]() si pulsatia de intalnire prin relatia
si pulsatia de intalnire prin relatia ![]() .
Acest factor este invers factorului de amplificare a miscarii si reprezinta
raportul dintre amplitudinea valului si amplitudinea miscarii.
.
Acest factor este invers factorului de amplificare a miscarii si reprezinta
raportul dintre amplitudinea valului si amplitudinea miscarii.
Coeficientul total de amortizare, utilizand teoria fasiilor, se determina din expresia:
![]() (168)
(168)
Ecuatia diferentiala a miscarii devine:
![]()
iar
dupa impartire cu ![]()
![]() . (170)
. (170)
S-a introdus notatia
![]() , (171)
, (171)
ce reprezinta factorul de amortizare.
Solutia ecuatiei diferentiale (170) este:
![]() . (172)
. (172)
Constantele C1 si C2 se determina din conditiile initiale.
Astfel, in momentul initial cand t = 0, inclinarea ![]() si viteza unghiulara a navei
si viteza unghiulara a navei ![]() .
.
Rezulta ![]() si
si ![]() .
.
Introducand valorile lui C1 si C2 in relatia (172) se obtine:
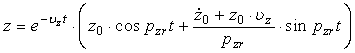
sau sub forma armonica
![]() (174)
(174)
In relatia (174) s-au notat expresiile:
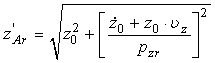
![]() (176)
(176)
amplitudinea initiala a miscarii si faza initiala a oscilatiilor verticale amortizate pe apa linistita.
Legea de miscare a oscilatiilor verticale cu amortizare devine:
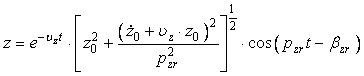
sau sub forma
![]() (178)
(178)
unde: ![]() este amplitudinea oscilatiilor verticale
amortizate, libere, care descreste dupa o lege exponentiala in timp (fig. 12)
este amplitudinea oscilatiilor verticale
amortizate, libere, care descreste dupa o lege exponentiala in timp (fig. 12)
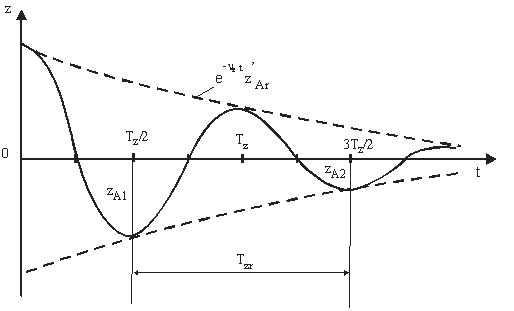
Fig. 12
Din ecuatia (178) se observa ca oscilatia verticala este o miscare
oscilatorie armonica amortizata, avand pulsatia ![]()
si
perioada 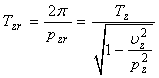 . (179)
. (179)
Amplitudinea descreste la o perioada de timp cu valoarea decrementului logaritmic:
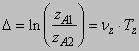 (180)
(180)
Daca se determina experimental decrementul logaritmic, utilizand relatiile
(179) si (180), se poate calcula factorul de amortizare ![]()
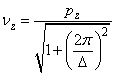 (181)
(181)
Timpul de amortizarea a oscilatiilor t, daca se adopta o valoare pentru raportul ![]() si se calculeaza
si se calculeaza 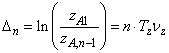 ,
se determina cu relatia:
,
se determina cu relatia:
![]() (182)
(182)
In figura 12 este reprezentat graficul de variatie in timp a elongatiei miscarii oscilatorii a navei, data de legea (178).
Oscilatia verticala pe valuri regulate in coordonate absolute
Se considera o nava pe valuri avand unghiul de intalnire ![]() .
.
Ecuatia diferentiala a miscarii in forma simplificata este:
![]() (183)
(183)
Se imparte ecuatia cu ![]() si obtine forma
si obtine forma
![]() (184)
(184)
Ecuatia (184) admite solutia ![]() ,
unde
,
unde ![]() este solutia ecuatiei omogene, iar
este solutia ecuatiei omogene, iar ![]() este solutia particulara.
este solutia particulara.
Consideram membrul doi egal cu zero si se obtine solutia ecuatiei omogene de forma
![]()
![]() (185)
(185)
Solutia particulara ![]() este de forma:
este de forma:
![]() (186)
(186)
Punem conditia ca ![]() sa verifice ecuatia (184) si se obtine:.
sa verifice ecuatia (184) si se obtine:.
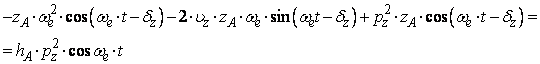
Solutia
particulara satisface ecuatia diferentiala pentru orice valori ![]() .
Se iau doua valori
.
Se iau doua valori ![]() si
si ![]() ,
obtinandu-se sistemul de ecuatii cu necunoscutele
,
obtinandu-se sistemul de ecuatii cu necunoscutele ![]() si
si ![]() :
:
![]()
![]() (189)
(189)
Ridicand la patrat cele doua ecuatii si adunandu-le rezulta expresia amplitudinii miscarii
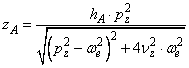
Din ecuatia (189) se obtine expresia defazajului dintre miscarea de oscilatie si excitatie
![]() (191)
(191)
Daca se noteaza
: ![]() - coeficient de amortizare si
- coeficient de amortizare si
![]() - pulsatia relativa a valului sau factor de
acordaj,
- pulsatia relativa a valului sau factor de
acordaj,
expresiile (190) si (191) devin:
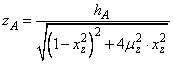 (190')
(190')
si 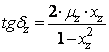 . (191') . Din
expresiile legilor de miscare (185) si (186) se poate observa ca oscilatia
naturala are pulsatia de la miscarea amortizata pe apa linistita si amplitudinea
variabila dupa o lege exponentiala, iar oscilatia fortata are pulsatia valului
si amplitudinea constanta data de relatia (190).
. (191') . Din
expresiile legilor de miscare (185) si (186) se poate observa ca oscilatia
naturala are pulsatia de la miscarea amortizata pe apa linistita si amplitudinea
variabila dupa o lege exponentiala, iar oscilatia fortata are pulsatia valului
si amplitudinea constanta data de relatia (190).
Deoarece oscilatia naturala se amortizeaza in timp, legea oscilatiei fortata stabilizata este
![]()
Se analizeaza variatia amplitudinii oscilatiei stabilizate functie de
factorul de acordaj ![]() .
Se introduce notiunea de factor de amplificare
.
Se introduce notiunea de factor de amplificare ![]() dat de relatia
dat de relatia
 (193)
(193)
In activitatea practica, intereseaza in mod deosebit amplitudinea si
defazajul miscarii oscilatorii. In acest sens se vor reprezenta graficele de
variatie ale marimilor ![]() (fig. 13) si
(fig. 13) si ![]() (fig. 14)
(fig. 14)
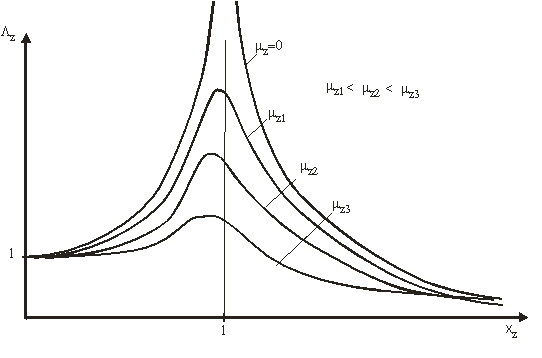
Fig.13
a)
Pentru ![]() rezulta
rezulta ![]() .
Nava oscileaza pe un val cu lungime foarte mare sau are o masa foarte mica. In
acest caz nava oscileaza odata cu suprafata valului.
.
Nava oscileaza pe un val cu lungime foarte mare sau are o masa foarte mica. In
acest caz nava oscileaza odata cu suprafata valului.
b)
Pentru ![]() rezulta
rezulta ![]() .
Este cazul real de exploatare pe valuri cu perioade mici sau nava are o arie a
suprafetei de plutire foarte mica sau o masa foarte mare.
.
Este cazul real de exploatare pe valuri cu perioade mici sau nava are o arie a
suprafetei de plutire foarte mica sau o masa foarte mare.
c)
Pentru ![]() ,
cazul de rezonanta,
,
cazul de rezonanta, ![]() .
Factorul de amplificare depinde de coeficientul de amortizare al navei.
Amplitudinea oscilatiei este cu atat mai mare cu cat coeficientul de amortizare
este mai mic
.
Factorul de amplificare depinde de coeficientul de amortizare al navei.
Amplitudinea oscilatiei este cu atat mai mare cu cat coeficientul de amortizare
este mai mic
Punctele de extem ale factorului de amplificare se obtin din egalarea
cu zero a primei derivate a functiei 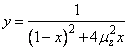 in raport cu x, introducandu-se notatiile
in raport cu x, introducandu-se notatiile ![]() si
si ![]() .
.
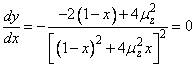 ,
,
din care rezulta
![]() si
si
![]() sau daca se revine la marimile initiale,
considerand numai solutia pozitiva
sau daca se revine la marimile initiale,
considerand numai solutia pozitiva
![]() (194)
(194)
Din aceasta relatie se observa ca factorul de amplificare este maxim la valori mai mici decat 1, valoare ce corespunde rezonantei fara amortizare. Cunoscand pozitia de maxim, prin inlocuire in relatia (193), se obtine
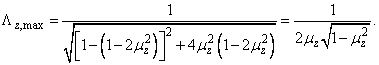
In figura 13 sunt reprezentate mai multe curbe de variatie a factorului de amplificare functie de factorul de racordaj, pentru diversi coeficienti de amortizare.Deoarece coeficientul de amortizare este foarte mic in comparatie cu unitatea, se considera ca pozitia si valoarea maxima a factorului de amplificare se afla in zona de rezonanta.
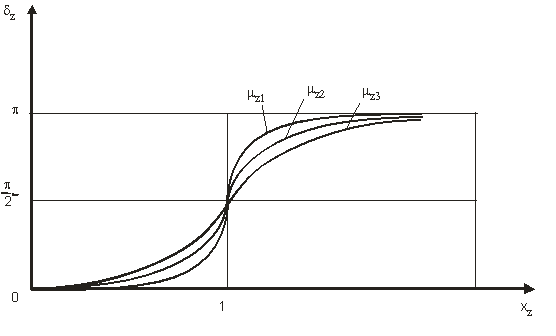
Fig.14
Din reprezentarea grafica a defazajului (fig. 14) se pot observa urmatoarele cazuri:
a)
Pentru![]() ,
,
![]()
![]() si
si ![]() .
Momentul perturbator este in faza cu unghiul de panta al valului;
.
Momentul perturbator este in faza cu unghiul de panta al valului;
b)
Pentru ![]()
![]()
![]() si
si ![]() ;
;
c)
Pentru ![]()
![]()
![]() si
si ![]() ;
;
d)
Pentru ![]()
![]()
![]() si
si ![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 9339
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved