| CATEGORII DOCUMENTE |
Reprezentarea sistemelor Lindenmayer ca documente XML
Rezumat
In aceasta lucrare se prezinta LSML (L-Systems Modeling Language) - un limbaj structurat de definire a sistemelor Lindenmayer (L-sisteme), ca aplicatie a meta-limbajului XML (eXtensible Markup Language). Documentele LSML vor putea fi utilizate pe Web si integrate in alte documente XML, precum XHTML si Web Schematics sau in aplicatii hipermedia distribuite.
Cuvinte cheie XML, Web, sisteme dinamice, fractali, documente, grafica, limbaje formale
Dezvoltarea accentuata a Internetului si mai ales a Web-ului a dus la aparitia meta-limbajului structurat XML (eXtensible Markup Language), descendent al SGML (Standard Generalized Markup Language). Limbajul XML ofera suport pentru specificarea si validarea - printr-o constructie definind structura unui document denumita DTD (Document Type Definition) - a documentelor complexe. XML este independent de platforma hardware si software, fiind un meta-limbaj simplu de utilizat, folosit pentru definirea unor noi tipuri de documente prin intermediul unei specificatii formale. Un document XML consta dintr-o secventa de elemente (marcatori delimitati de < si >), fiecare element putand include recursiv alte elemente sau text si putand avea atasate diverse atribute. Fiecare element va poseda un marcator de inceput si un marcator de sfarsit, regulile de imbricare a elementelor si numarul, modul de aparitie si tipul atributelor fiind definite in mod formal de definitia tipului de document (DTD) atasata fiecarei clase de documente care se doreste a fi specificata.
Datorita flexibilitatii limbajului XML, in prezent exista o multitudine de aplicatii, una dintre cele mai importante fiind interschimbarea datelor electronice intre diverse locatii de pe Web. Alte directii de cercetare includ: MathML, un limbaj menit sa reprezinte formulele matematice intr-un mod consistent si independent de editor, QL (Query Language), destinat modelarii inte-rogarilor de baze de date distribuite, sau EFDL (Extensible Forms Description Language), limbaj utilizat pentru descrierea formularelor electronice etc.
Vom defini un tip de document XML pentru reprezentarea sistemelor dinamice Lindenmayer (fractalii L-sistem), specificand DTD-ul pentru limbajul LSML (L-Systems Modeling Language) si vom ilustra o parte dintre posibilele lui utilizari viitoare. Se va urmari si definirea riguroasa a L-sistemelor pe baza careia vom dezvolta elementele limbajului LSML.
Un sistem Lindenmayer (L-sistem) este un tip particular de sistem dinamic simbolic in care evolutia sistemului poseda o interpretare geometrica bazata pe grafica turtle si a fost introdus de Aristid Lindenmayer (1968) pentru a modela dezvoltarea biologica. Un L-sistem poate fi definit formal de un 6-uplu:
Ls # alphabet, axiom, rules, order, angle, colour ñ
fiind construit din segmente de linii folosind un set de reguli (rules) care specifica diverse comenzi de desenare.
Pornind de la un sir initial numit axioma (axiom) sau initiator, un sir de simboluri w I V* , unde V este un alfabet (alphabet) de simboluri, vor fi aplicate de un anumit numar de ori (definind ordinul fractalului, dat de order I N^) anumite reguli de transformare pentru a produce un sir final continand comenzi folosite pentru reprezentarea fractalului dorit. Se mai precizeaza valoarea unghiului angle I (1, 360) si culoarea initiala (colour I N) folosite in cadrul regulilor de desenare. Regulile sunt similare productiilor gramaticilor din teoria limbajelor formale, putand contine atat comenzi de desenare, cat si neterminali folositi in generarea sirului final. Regulile (productiile sau legile de rescriere) au forma n w, unde n I V, w I V*, cu V # N È C, in care N este multimea neterminalilor folositi in definirea L-sistemului, iar C este multimea comenzilor de desenare permise (vezi sectiunea 2.4). Pot exista, de asemeni, si reguli de stergere. Daca un simbol n I V nu are asociata o productie data in mod explicit, atunci se considera ca este asociat lui insusi si reprezinta o constanta a sistemului Lindenmayer. Axioma poate contine comenzi de desenare si macar un simbol neterminal (se permite folosirea ca neterminali a numelor comenzilor de desenare).
Evolutia unui L-sistem este definita de o secventa (gi), i # 0, 1, 2, , unde fiecare generatie gi este un cuvant din V* obtinut prin aplicarea regulilor (in paralel) tuturor simbolurilor din cuvantul gi-1, prima generatie fiind axioma. Evolutia unui L-sistem modeleaza intr-o maniera simpla si concisa dezvoltarea unei populatii de forme biologice.
In functie de tipul de reguli de productie, un L-sistem poate fi independent sau dependent de context. La fel, in functie de numarul de reguli ce pot fi aplicate la un pas in evolutia unui sistem, un L-sistem poate fi determinist sau nederminist. Daca exista mai mult de o regula de aplicare pentru un anumit simbol (de exemplu avem a w1 si b w2, cu a, b I V, w1, w2 I V*), atunci este nevoie de un criteriu de alegere de aplicare a unei reguli. In cazul in care aceasta alegere se realizeaza in functie de anumite probabilitati asociate fiecarei reguli in parte, sistemul Lindenmayer se numeste stohastic. In continuare ne vom referi numai la L-sisteme deterministe, independente de context, denumite si DOL-sisteme. O clasa de DOL-sisteme este cea a BDOL-sistemelor (bracketed L-Systems), utile pentru modelarea matematica a structurilor (biologice) ramificate.
De fapt, limbajele generate de L-sisteme apartin clasei limbajelor recursiv-enumerabile. Aspectele spe-cifice L-sistemelor sunt acelea referitoare la evolutia paralela a unui cuvant (generatii) pe baza generatiei precedente si la reprezentarea grafica a sirului rezultat in urma unui numar de generatii succesive.
Radomir Mech si Przemyslaw Prusinkiewicz (1996) au propus un nou tip de L-sistem numit Open L-system, in vederea modelarii formale a interactiunii dintre plante si mediu prin intermediul proceselor comunicante.
Consideram urmatorul sistem Lindenmayer denumit L-sistem Fibonacci:
F # , a, , w ñ
unde am omis angle si colour. Putem pune in corespondenta cu acest L-sistem relatiile recursive definind sirul Fibonacci (f0 # f1 # 1, fn^2 # fn^1 ^ fn, cu n ³ 0). Se demonstreaza usor ca numarul de organisme la a n-a generatie gn este êgn ê # fn. Putem observa ca gn^2 # gn^1gn (de exemplu g7 # (babbababbabba)(babbabab) # g6 g5).
In cadrul unui L-sistem dinamic se poate pune in evidenta un proces local (afectand fiecare organism individual si fiind reprezentat de aplicarea unei reguli de productie unui simbol particular) care duce la aparitia in fapt a unui proces global, la nivelul intregii populatii. Evolutia locala se desfasoara in paralel, in intreaga populatie, similar procesului de dezvoltare observat la plante.
Din acest aspect deriva o parte din preocuparile matematicienilor de a modela dezvoltarea biologica cu ajutorul L-sistemelor. O alta utilizare este studiul dinamic al suprafetelor geodezice (L-sisteme Thue-Morse) ori simularea tesuturilor nervoase (arbori de dendrite si axoni neuronali). Se cunosc si instante ale problemei comisului voiajor modelate ca sisteme Lindenmayer (Adrian Mariano, 1995). Diverse L-sisteme (e.g. Penrose tiles) au fost utilizate pentru rezolvarea problemei acoperirii planului.
Seymour Papert (1967) a inventat grafica turtle ca un sistem pentru translatarea unei secvente de simboluri ale unui alfabet in miscari ale unui automat, numit broasca (turtle) pe un mediu de vizualizare (ecran grafic), oferind astfel copiilor un obiect programabil pentru facilitarea invatarii informaticii (prin intermediul limbajului LOGO). Sistemul de baza este urmatorul: fixam un pas d reprezentand distanta in pixeli parcursa de broasca in cadrul unei operatiuni de miscare. Se mai defineste un unghi u, in mod uzual u # 360/n, cu 1 £ n £ 360. Pentru reprezentari mai complexe se poate modifica si culoarea segmentelor de dreapta figurate. In acest mod, L-sistemul este definit complet.
Comenzile standard de desenare (apartinand multimii de comenzi C) sunt inspirate din limbajul LOGO (grafica turtle). Iata o parte dintre ele:
F (forward) deseneaza trasand o linie inainte
G (go) deplaseaza broasca, fara desenare
(increment) roteste broasca cu unghiul u ales, in sens trigonometric
(decrement) roteste broasca cu unghiul u ales, in sens anti-trigonometric
(turn) incearca sa se intoarca cu 180 de grade
(reverse) inverseaza sensurile comenzilor + si -
n incrementeaza unghiul cu n grade
/n decrementeaza unghiul cu n grade
Cn schimba culoarea la culoarea n
<n incrementeaza culoarea cu n
>n decrementeaza culoarea cu n
@n multiplica lungimea segmentului de linie cu n
Starea broastei este definita de tripletul (x, y, a), unde x si y reprezinta pozitia curenta a broastei, iar unghiul a este interpretat ca directie de translare a broastei. Pentru generarea de forme grafice 3D, starea broastei este data de 6-uplul (x, y, z, a b d), in care (x, y, z) sunt coordonate in spatiul cartezian tridimensional, iar unghiurile a b si d modeleaza orientarea curenta a broastei.
Consideram urmatorul exemplu clasic (simbolul din cadrul regulilor il vom inlocui cu #, iar comenzile Angle si Axiom vor preciza unghiul initial u si, respectiv, axioma):
Dragon
, Fx, , 5, 8, 0 ñ in care am considerat order # 5 si colour # 0 (negru). Inlaturand comenzile de desenare, L-sistemul consta din regulile de productie urmatoare: a ab si b ba, avand drept axioma simbolul a I V, cu V # . Benoit Mandelbrot numeste acest tip de L-sistem dragonul Harter-Heighway.
In urma aplicarii regulilor de desenare, pentru exemplul de mai sus se va genera sistemul Lindenmayer din figura 1. Pentru un numar mare de iteratii, reprezentarea grafica (denumita si curba Dragon) este ilustrata in figura 2. Pentru order tinzand la infinit, reprezentarea L-sistemului se numeste atractor. Mai mult, din figura 2 se poate remarca deja proprietatea de auto-similaritate a sistemului Dragon. Astfel, pentru majoritatea L-sistemelor se pot asocia doua numere, unul desemnand numarul de forme "congruente" in care este divizata reprezentarea in intregul ei si celalalt definind un "factor de scalare" a fiecarei forme din cadrul reprezentarii.
Datorita faptului ca multe forme biologice au un aspect "fragmentat" sau "ramuros" in dezvoltarea lor, in grafica turtle se vor defini doua noi comenzi push si pop care vor pune, respectiv vor extrage, de pe stiva starea unui L-sistem (clasa BDOL-sistemelor). Comanda push va fi reprezentata de simbolul s, iar push va fi reprezentata de t. Pentru sistemele Lindenmayer tridimensionale, operatiunile increment si decrement vor fi inlocuite de sase comenzi de rotatie 3D, cite o pereche pentru fiecare din cele trei axe Ox, Oy si respectiv Oz.
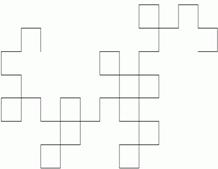
Figura L-sistemul Dragon de ordinul 5

Figura Curba Dragon
Exista diverse aplicatii destinate reprezentarii grafice a L-sistemelor, fiecare avand, din pacate, propriul format de stocare a datelor.
Unul dintre cele mai performante programe este Lparser, conceput de Laurens J.Lapre, care suporta definirea si reprezentarea L-sistemelor tridimensionale, formele grafice putand fi stocate in formate ca VRML, DXF sau POV. Drept componente suplimentare, bazate pe Lparser, se pot enumera LMUSe care genereaza, conform regulilor de rescriere, fisiere audio MIDI (Music Instrument Digital Interface) si LPEvol (Lparser Evolution Engine) - shell Java pentru analiza si reprezentarea grafica a L-sistemelor.
Ca alte exemple putem mentiona: Graphtal (sub UNIX) pentru simularea DOL-sistemelor parametrice, Plant and Fractal Generator 2D (pentru Macintosh), FRACTINT (sub DOS si Windows), L-systems Applet (pentru Web), toate fiind disponibile gratuit.
Figura 3: Airhorse (un L-sistem vizualizat intr-un mediu VRML, parte din proiectul Nerve Garden)
Un proiect spectaculos al organizatiei Biota este Nerve Garden, bazat pe L-sisteme, VRML, retele neuronale, tehnologii Web si tehnici de codificare genetica, al carui scop este explorarea interactiva a biologiei digitale pe Internet si, intr-un viitor mai departat, instituirea unei infrastructuri pentru medii virtuale biologice si crearea unor noi organisme (plante si animale) artificiale.
In continuare vom defini tipul de documente LSML conform standardului XML, un tip de document fiind definit formal de partile sale constituiente si de structura acestora, prin intermediul definitiei tipului de document (Definition Type Document - DTD). DTD este exprimata ca un set de afirmatii (instructiuni) declarative, utilizand o sintaxa speciala. Fiecare definitie de element (marcator sau tag) al limbajului este compusa din trei parti: un nume sau un grup de nume (neterminali in jargonul limbajelor formale), doua caractere specificand regulile de minimizare (vezi mai jos) si un continut (neterminali si terminali), fiecare definitie putand fi asimilata cu o regula de productie. Partile componente ale unei declaratii sunt separate de spatii albe.
Regulile de minimizare determina daca tag-urile de inceput si de sfarsit de element trebuie sa fie prezente la fiecare aparitie a respectivului element. Regulile sunt de fapt perechi de caractere: primul se refera la tag-ul de start, iar cel secund la tag-ul de sfarsit. Pot fi prezente numai caracterele '-' (marcator obligatoriu) si 'o' (marcator optional). In XML nu sunt permise tag-uri de sfarsit optionale, un element fara tag de sfarsit avand o sintaxa modificata.
Inchisa intre paranteze, a treia parte a definitiei unei element se numeste model-continut, specificand ce alte elemente pot apare in cadrul elementului definit. Cuvantul cheie #PCDATA (parsed character data) indica posibilitatea aparitiei oricarui caracter valid. Alte tipuri de date permise: CDATA (character data), NDATA (non-XML data), EMPTY (no data - element vid), ANY (orice tip de data) etc.
In declaratia unui model-continut putem include un semn special, denumit indicator de aparitie, care poate fi: semnul plus (elementul respectiv poate apare de una sau mai multe ori), semnul asterisc (elementul poate apare de zero, unu sau mai multe ori) sau semnul intrebarii (elementul poate apare cel mult o data).
Un model-continut poate cuprinde mai multe componente intr-o anumita ordine dictata de un conector. Un astfel de conector este unul din urmatoarele caractere: virgula (componentele trebuie sa apara obligatoriu in ordinea specificata), ampersand (componentele trebuie sa apara toate, dar in ordine aleatoare) ori bara verticala (doar una dintre componente poate apare).
Un anumit element poate poseda un set de atribute utilizate sa descrie o anumita proprietate a unei aparitii specifice (particulare) a acelui element. Atributele vor fi specificate numai in cadrul tag-ului de start, dupa numele elementului, ele declarandu-se in cadrul DTD, tipurile valorilor acceptate fiind: ID (identificator unic pentru fiecare instanta a elementului), CDATA (orice sir de caractere valide), ENTITY (nume de entitate generala), NUMBER (doar numerele intregi sunt acceptate ca valori) etc.
A treia parte a definitiei unui atribut specifica modul de interpretare a absentei atributului respectiv. Pot fi utilizate si aici o serie de cuvinte cheie predefinite: #REQUIRED (valoarea trebuie specificata in mod obligatoriu), #IMPLIED (valoarea poate lipsi) si altele.
Limbajul XML poseda o metoda flexibila si facila de codificare si referentiere a diferitelor parti ale continutului unui document, intr-un mod portabil, prin intermediul entitatilor (un fel de macro-uri). O forma speciala de entitati, numite entitati parametru, pot fi utilizate in declaratiile XML din cadrul DTD, dupa cum vom vedea mai jos.
Conform definitiei formale a unui sistem Lindenmayer, vor trebui specificate: numele L-sistemului, unghiul si culoarea initiale folosite in reprezentarea grafica, axioma (compusa dintr-un sir de simboluri, neterminali sau comenzi de desenare), regulile de productie si numarul de aplicare in paralel a lor (gradul L-sistemului). Vom lua in consideratie doar sistemele Lindenmayer deterministe si independente de context, avand reprezentari grafice bidimensionale, desi modelul propus poate fi folosit si pentru alte tipuri de L-sisteme.
Vom defini pentru inceput elementele limbajului, apoi atributele aferente fiecarui element considerat.
<!ENTITY % command
'forward | left | right | colour |
reverse | turn | push | pop'>
<!ELEMENT lsystem --
(axiom, rules)>
<!ELEMENT axiom -- ((%command; | symbol)*)>
<!ELEMENT rules -- (rule*)>
<!ELEMENT rule -- ((%command; | symbol)*)>
<!ELEMENT symbol -- (#PCDATA)>
<!ELEMENT forward -- EMPTY>
<!ELEMENT left -- EMPTY>
<!ELEMENT right -- EMPTY>
<!ELEMENT colour -- EMPTY>
<!ELEMENT reverse -- EMPTY>
<!ELEMENT turn -- EMPTY>
<!ELEMENT push -- EMPTY>
<!ELEMENT pop -- EMPTY>
Dupa cum se remarca din definitiile de mai sus, un document LSML va defini un L-sistem, fiind compus din elementele axiom si rules. Aceste elemente vor contine fie simboluri neterminale (date prin intermediul elementelui symbol), fie comenzi de desenare (elemente de tip command). Elementul left substituie comanda decrement, iar elementul right inlocuieste increment. Comanda go se obtine prin constructia <forward draw='off'>, iar comanda @ prin <forward lenght=''> (vezi atributele de mai jos).
Pentru aceste elemente, atributele asociate sunt urmatoarele:
<!ATTLIST lsystem
name PCDATA #REQUIRED
author PCDATA #REQUIRED
angle PCDATA #REQUIRED
colour PCDATA #IMPLIED
>
<!ATTLIST rules
repeat NUMBER #REQUIRED
>
<!ATTLIST rule
start PCDATA #REQUIRED
>
<!ATTLIST forward
draw on | off 'on'
lenght NUMBER #IMPLIED
>
<!ATTLIST left
degree NUMBER #IMPLIED
axis PCDATA #IMPLIED
>
<!ATTLIST right
degree NUMBER #IMPLIED
axis PCDATA #IMPLIED
>
<!ATTLIST colour
value PCDATA #IMPLIED
inc NUMBER #IMPLIED
dec NUMBER #IMPLIED
>
<!ATTLIST push
stack PCDATA #IMPLIED
>
<!ATTLIST pop
stack PCDATA #IMPLIED
>
Atributele asociate elementelor LSML permit specificarea unui set mai larg de L-sisteme (am inclus atributul axis pentru specificarea axei pentru care se modifica unghiul broastei, util pentru sisteme 3D, iar comenzile push si pop permit salvarea in si respectiv extragerea de informatii din mai multor stive prin intermediului atributului stack, permitandu-se astfel definirea de sisteme Lindenmayer cu stive multiple). In cadrul unui element rule, atributul start nu trebuie neaparat sa contina numai un neterminal, dandu-se in acest mod posibilitatea specificarii de L-sisteme dependente de context.
Vom rescrie definitia L-sistemului Dragon din sectiunea 2.4 ca document LSML:
<?xml version='1.0'>
<!DOCTYPE lsystem PUBLIC '-//LSML 1.0//EN'>
<lsystem name='dragon' author='Sabin Corneliu Buraga' angle='8'>
<axiom>
<forward />
<symbol>x</symbol>
</axiom>
<rules repeat='5'>
<rule start='y'>
<right />
<forward />
<symbol>x</symbol>
<left />
<left />
<forward />
<symbol>y</symbol>
<right />
</rule>
<rule start='x'>
<left />
<forward />
<symbol>x</symbol>
<right />
<right />
<forward />
<symbol>y</symbol>
<left />
</rule>
</rules>
</lsystem>
Se putea renunta la elementul symbol, insa l-am preferat din motive de claritate a documentului-sursa.
Modelul orientat-obiect pentru documente (Document Object Model - DOM) reprezinta o interfata de programare a aplicatiilor destinate sa prelucreze documentele XML si HTML, independenta de platforma si de limbaj, definind structura logica a documentelor si modalitatile de accesare si de modificare a lor. Aceasta structura logica este una arborescenta, orientata-obiect: documentele sunt modelate utilizand obiecte, iar modelul nu ofera doar o vizualizare structurata a documentului, ci si o maniera de specificare a comportamentului sau si a obiectelor componente. Fiecare element al unui document poate fi privit, deci, ca un obiect, fiecare obiect avand identitate si propriile sale functii. DOM identifica interfetele si obiectele utilizate sa reprezinte si sa manipuleze un document, semantica acestor interfete si obiecte (inclusiv comportamentul si atributele lor) si relatiile si dependentele intre aceste interfete si obiecte.
LSML fiind derivat din meta-limbajul XML, pentru scrierea aplicatiilor poate fi folosit DOM deja specificat de Consortiul Web pentru XML, fiind standardizat doar primul nivel, urmand a fi supus standardizarii si nivelul secund al modelului. In plus, ne propunem ca in viitor sa definim un model obiectual specific documentelor LSML.
Principalul avantaj al reprezentarii L-sistemelor ca documente LSML este independenta de platforma hardware si software, acest format putand fi folosit ca modalitate de interschimbare a definitiilor de sisteme Lindenmayer intre diverse programe de modelare a lor.
Documentele LSML sunt mai lizibile si mai usor de prelucrat decat fisierele de date (nestructurate) utilizate de diverse programe de reprezentare a sistemelor Lindenmayer ca Lparser sau L-systems Applet.
Fiind derivat din XML, limbajul LSML poate fi integrat in alte limbaje de adnotare, ca de exemplu in XHTML, succesor al HTML, in WebSchematics, utilizat in efectuarea de scheme si de ilustratii pe Web, in VML (Vector Markup Language) sau SVG (Scalable Vector Graphics), pentru reprezentarea imaginilor vectoriale.
Modelul obiectual pentru LSML ofera suport in dezvoltarea de aplicatii de manipulare a documentelor, in limbaje precum Java sau C++.
Reprezentarea L-sistemelor in LSML ofera o mai mare usurinta de procesare in paralel a regulilor de productie, deoarece structura arborescenta a documentelor permite utilizarea unor tehnici de accesare si de cautare paralele. Aceasta poate duce la accelerarea reprezentarii grafice a sistemelor Lindenmayer.
LSML poate fi integrat in proiectul Nerve Garden ca mijloc universal de reprezentare a formelor biologice descrise de L-sisteme in medii virtuale distribuite, L-sistemele 3D stocate ca documente LSML putand fi convertite ulterior in obiecte VRML.
In prezenta lucrare am definit un limbaj derivat din XML pentru reprezentarea eleganta, independenta de hardware si de software, a sistemelor Lindenmayer, avand multiple utilizari in domenii ca biologia, simularea computerizata sau grafica de sinteza.
Limbajul specificat, L-System Modeling Language, poate fi folosit pentru interschimbarea reprezentarilor L-sistemelor in diverse programe de vizualizare sau pentru integrarea fractalilor L-sistem in alte documente XML ori in paginile Web. De asemeni, operatiile de cautare in astfel de structuri pot fi efectuate in paralel. Ne propunem ca pe viitor sa oferim si un model orientat-obiect pentru documentele LSML in vederea conceperii de aplicatii Web de prelucrare distribuita a L-sistemelor, sa studiem posibilitatile de integrare completa in limbaje de specificare a graficii pe calculator precum Web Schematics sau VML si sa realizam o aplicatie de vizualizare si prelucrare a documentelor LSML.
T.Bray, J.Paoli, C.M.Sperberg-McQueen (eds.) - "Extensible Markup Language (XML)", W3C, nov.1997: https://www.w3.org/TR/REC-xml
B.F.Damer - "Amoeba: a Simulator for Molecular Nanotechnology", The Fouth Foresight Conference on Molecular Nanotechnology, Paco Alto, 1995
R.M.Dickau - "Three-dimensional L-Systems": https://forum.swarthmore.edu/advanced/robertd/ lsys3d.html
D.Duce, B.Hopgood - "Web Schematics on WWW", Web Consortium's Note, mart.1998: https://www.w3.org/TR/1998/NOTE-WebSchematics
M.Hammel - "L-Systems Software": https://www.cpsc.ucalgary.ca/Ihammel/BioSim/ Lsystems/software/software.html
T.Jucan - "Limbaje formale si automate", Ed. MatrixRom, Bucuresti, 1999
L.Lapre - "Lparser": https://www.xs4all.nl/Iljlapre
T.Lin - "Animation of L-system based 3-D Plant Growing in Java", Maryland Univ., nov.1996: https://www.cs.umbc.edu/Iebert/693/TLin/
B.Mandelbrot - "The fractal geometry of nature", W.H. Freeman, San Francisco, 1982
B.Mandelbrot - "Obiectele fractale", Ed.Nemira, Bucuresti, 1998
A.Mariano, P.Moscato, M.Norman - "Using L-Systems to generate arbitrarily large instances of the Euclidean Traveling Salesman Problem with known optimal tours", Anales del XXVII Simposio Brasileiro de Pesquisa Operacional, Victoria, Brazil, nov.1995: ftp://ftp.ing.unlp.edu.ar/pub/ papers/memetic/final.ps.Z
M.Masse - "L-system Applet": https://ugrad-www.cs.colorado.edu/ masse/Java/Lsystem/Lsys.html
S.Papert - "Mindstorms: Children, Computers, and Powerful Ideas", Basic Books, NewYork, 1980
P.Prusinkiewicz, A. Lindenmayer - "The Algorithmic Beauty of Plants", Springer-Verlag, NewYork, 1990
P.Prusinkiewicz, L.Kavi - "Subapical bracketed L-systems", in Grammars and Their Application to Computer Science, LCNS 1073, Springer-Verlag, Berlin, 1996
P.Prusinkiewicz, M.Hammel - "Language-Restricted Iterated Function Systems, Koch Constructions, and L-systems", in New Directions for Fractal Modeling in Computer Graphics, SIGGRAPH'94 Course Notes, ACM Press, 1994
G.Rozenberg, A.Salomaa - "Lindenmayer Systems: Impacts on Theoretical Computer Science, Computer Graphics, and Developmental Biology", Springer-Verlag, Berlin, 1992
D.Skillicorn - "Structured Parallel Computation in Structured Documents", Journal of Universal Computer Science, vol.3, no.1, 1997
M.Taylor, J.P.Louvet - "sci.fractals Frequently Asked Questions", 1998: https://www.mta.ca/ Imctaylor/sci.fractals-faq/
J.Vaario, K.Shimohara - "Modeling Environment Sensitive L-systems", Kyoto Conference on Mathematical Biology'96, Japon, 1996
L.Wood (ed.) - "Document Object Model (DOM) Level 1 Specification", Web Consortium, oct.1998: https://www.w3.org/TR/REC-DOM-Level-1
D.Wright - "Dynamical Systems and Fractals": https://www.math.okstate.edu/mathdept/dynamics/ lecnotes/
* * * - "FRACTINT Web Pages": https://spanky.triumf.ca/www/fractint/
* * * - "Live Alife Page": https://www.fusebox.com/cb/alife.html
* * * - "VRML Resources": https://www.vrml.com
* * * - "World-Wide Web Consortium's Technical Reports", Boston, 2000: https://www.w3.org/TR/
Autor:
Sabin-Corneliu Buraga
Facultatea de Informatica, Universitatea "A.I.Cuza", Iasi
Email: busaco@infoiasi.ro
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1814
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved