| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
CINETICA REACTIILOR CHIMICE
1. CONSIDERATII GENERALE
Cinetica chimica studiaza desfasurarea in timp a reactiilor chimice, ocupandu-se cu determinarea vitezei acestora, cu descrierea evolutiei sistemului chimic de la starea initiala la cea finala. In abordarea cinetica, sistemul evolueaza catre o noua stare de echilibru. Descrierea sistemului se poate face in doua moduri care constituie cele doua laturi ale cineticii chimice. In primul dintre acestea, transformarea poate fi caracterizata fenomenologic prin masurarea unor marimi la diferite momente de timp (compozitia, presiunea, volumul), urmarindu-se masurarea vitezei de reactie. Al doilea mod de abordare se refera la descrierea mecanismului de reactie, adica cunoasterea etapelor intermediare pe care le parcurge un sistem intr-o transformare chimica. Aceste reactii care compun procesul global se numesc etape elementare. In multe reactii apar intermediari care sunt specii chimice nestabile cu viata foarte scurta, dar care iau parte efectiv la mersul reactiei.
VITEZA DE REACTIE. MODURI DE EXPRIMARE
Prin viteza de reactie se intelege variatia concentratiei reactantilor sau produsilor de reactie in unitatea de timp.
Se considera reactia generala:
aA + bB à cC + dD (1)
Pentru caracterizarea cantitativa a progresului unei reactii chimice este necesara definirea unui parametru care sa fie o masura a gradului de transformare. Cum reactia implica micsorarea numarului de moli de reactanti, respectiv cresterea numarului de moli de produsi, s-ar putea alege chiar numarul de moli.
Marimea se defineste conform relatiei:
![]()
unde: a, b, c, d = coeficientii stoechiometrici;
![]() = numarul de moli initial de reactanti, respectiv de produsi de reactie;
= numarul de moli initial de reactanti, respectiv de produsi de reactie;
![]() = numarul de moli de reactanti, respectiv de produsi de reactie, la un
timp t.
= numarul de moli de reactanti, respectiv de produsi de reactie, la un
timp t.
se numeste variabila de avansare sau de reactie si se poate scrie in general ca:
![]()
unde: νi = coeficient stoechiometric, negativ pentru reactanti si pozitiv pentru produsii de reactie;
ni = numarul de moli transformati din substanta i.
Exemplu: ![]()
Coeficientii stoechiometrici ai reactantilor se iau cu semn negativ deoarece ei se consuma in reactie, iar cei ai produsilor de reactie cu semn pozitiv, acestia formandu-se in urma reactiei.
ξ este o marime extensiva, dependenta de timp. Pentru a trece la o marime intensiva, se va imparti cu volumul sistemului. Se obtine variabila de conversie care se noteaza cu x:
![]() (5)
(5)
unde: ci = variatia de concentratie molara a substantei i;
V = volumul sistemului.
Pentru reactia generala considerata:
![]()
Deoarece ξ are aceeasi valoare pentru toti reactantii, viteza de reactie (r) se defineste conform relatiei:
![]() (7)
(7)
Inlocuind ξ cu relatia (2), se obtine pentru viteza de reactie:
![]() (8)
(8)
Este posibil sa se defineasca viteza in raport cu fiecare dintre reactanti sau produsi de reactie, fara raportarea la coeficientii stoechiometrici astfel:
![]() (9)
(9)
![]()
si
![]()
Deci, viteza de reactie a componentului i se defineste in modul urmator:
![]() (12)
(12)
unde: semnul (-) pentru reactanti; semnul (+) pentru produsi de reactie.
Viteza de reactie se poate defini si cu ajutorul variabilei de conversie x.
Inlocuind pe ξ in functie de x, relatia (7) devine:
![]() (13)
(13)
Daca se lucreaza intr-un sistem cu volumul constant, se poate folosi concentratia molara in definirea vitezei de reactie care devine:
![]() (14)
(14)
De exemplu, pentru reactia generala avem:
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
3. ORDIN DE REACTIE. MOLECULARITATE. LEGE DE VITEZA
O reactie chimica are loc numai intre molecule care se ciocnesc, iar viteza de reactie este proportionala cu frecventa ciocnirilor care la randul ei este proportionala cu produsul concentratiilor reactantilor.
Dependenta vitezei de reactie de concentratiile molare ale reactantilor, la temperatura constanta, este exprimata prin legea vitezei sau legea cinetica a actiunii maselor:
![]() (18)
(18)
unde: k = constanta de viteza sau viteza specifica;
n1, n2, , ni = ordinele partiale de reactie in raport cu reactantii respectivi (1, 2, , i);
c1, c2, , ci = concentratia molara a reactantilor 1, 2, .., i.
Constanta de viteza reprezinta viteza de reactie la concentratii molare unitare (1 mol/dm3) ale tuturor reactantilor.
Ordinele partiale de reactie difera in general de coeficientii stoechiometrici din ecuatia chimica.
Suma ordinelor partiale de reactie reprezinta ordinul total sau global de reactie (n):
![]() (19)
(19)
Ordinele de reactie pot avea valori pozitive, negative, zero, intregi sau fractionare.
Suma coeficientilor stoechiometrici a reactantilor dintr-o reactie chimica se numeste molecularitate (m), dar ea are semnificatie doar pentru procesele elementare (intr-o singura etapa).
Reactiile elementare care constituie procesul chimic pot avea viteze diferite si pot fi de ordine diferite. Una din reactiile elementare este cea mai lenta si va determina viteza globala a procesului. Aceasta etapa lenta se numeste etapa determinanta de viteza (e.d.v.).
Daca un reactant participant la stoechiometria globala are ordin de reactie zero, inseamna ca el participa la o reactie foarte rapida, urmand etapei determinante de viteza din mecanism.
4. CLASIFICAREA CINETICA A REACTIILOR CHIMICE
Reactiile chimice pot fi:
a) simple: se desfasoara intr-o singura etapa
b) complexe: se desfasoara in mai multe etape
a) Reactiile simple se clasifica dupa ordinul de reactie in:
reactii de ordinul intai: n = 1
reactii de ordinul al doilea: n = 2
reactii de ordinul al treilea: n = 3
reactii de ordin superior n
b) Reactiile complexe pot fi:
reactii opuse (reversibile)
A ![]() B (20)
B (20)
reactii paralele
A → P
A → R
reactii succesive (consecutive)
A → B → C (22)
reactii cu preechilibru
A
+ B ![]() C → P (23)
C → P (23)
5. CINETICA FORMALA A REACTIILOR SIMPLE
Urmarirea influentei concentratiei reactantilor asupra vitezei de reactie in conditii izoterme (T = const.), formeaza obiectul cineticii chimice formale. In general, ecuatiile sau legile de viteza sunt date sub forma diferentiala si ele necesita a fi integrate intre anumite limite pentru a determina variatia concentratiilor.
Se vor discuta reactii ireversibile care se desfasoara la volum constant.
5.1. Reactii de ordinul intai
Exista numeroase reactii in care sufera transformarea o singura substanta, iar viteza de reactie este proportionala cu concentratia acestui reactant.
O astfel de reactie decurge conform schemei:
aA → Produsi (24)
Ordinul de reactie este n = 1.
Concentratia molara se poate folosi la definirea vitezei de reactie deoarece volumul este constant.
Viteza de reactie este:
![]()
sau daca se foloseste variabila de conversie:
![]()
Stiind ca: ![]()
rezulta ca: ![]() (27)
(27)
Ecuatia (26) devine:
![]() (28)
(28)
Ecuatiile (25) si (28) sunt ecuatii cinetice diferentiale de ordinul I.
Separand variabilele in ecuatia (25)
si prin integrare intre limitele ![]() , cA si respectiv 0, t:
, cA si respectiv 0, t:
![]()
rezulta ecuatia cinetica integrata a reactiei de ordinul intai:
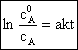 (30)
(30)
respectiv ![]()
Analog, separand variabilele in ecuatia (28) si integrand-o intre limitele 0, x si respectiv 0, t:
![]() (32)
(32)
Dupa integrare, rezulta ecuatia cinetica integrata de ordinul intai care contine variabila de conversie:
![]() (33)
(33)
Daca se trece de la logaritm la numar, se obtine variabila de conversie:
![]() (34)
(34)
In cele mai multe cazuri, coeficientul stoechiometric a este 1 si ecuatiile se simplifica.
Din ecuatia cinetica integrata (30) rezulta constanta de viteza k:
![]() (35)
(35)
Analiza dimensionala a ecuatiei (35) arata dimensiunea de timp-1 (s-1, min-1 sau h-1) a constantei de viteza.
Constanta de viteza se poate determina, folosind ecuatia cinetica integrata (30) in forma liniarizata si trecand la logaritm zecimal:
![]()
In
fig. 1. este prezentata forma liniarizata a ecuatiei cinetice integrate a
reactiei de ordinul intai (ecuatia 36), obtinandu-se o dreapta cu panta
negativa care are valoarea ![]() si permite determinarea
constantei de viteza k.
si permite determinarea
constantei de viteza k.
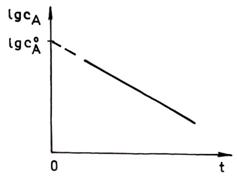
Fig. 1. Liniarizarea ecuatiei cinetice integrate
pentru reactia de ordinul intai
O marime des folosita pentru caracterizarea unei reactii este timpul de injumatatire t1/2 care este timpul in care concentratia substantei se reduce la jumatate.
Inlocuind
![]() in ecuatia (30) se obtine:
in ecuatia (30) se obtine:
![]()
Se constata ca timpul de injumatatire este independent de concentratia initiala.
Exemple tipice pentru reactii de ordinul intai sunt descompunerile termice ale unor compusi organici sau anorganici:
C2H5Cl
![]() C2H4 + HCl
C2H4 + HCl
2N2O5![]() 4NO2 + O2
4NO2 + O2
izomerizarea unor compusi organici (ciclobutena → 1,3-butadiena), reactiile nucleare de dezintegrare radioactiva, procese ce se desfasoara in solutii. In categoria reactiilor de ordinul intai se incadreaza reactiile care au loc in solutie, in care unul din reactanti (solventul) este prezent intr-un exces foarte mare astfel incat concentratia lui practic nu variaza in decursul reactiei. Aceste reactii se numesc reactii de ordin pseudo-unu. O astfel de reactie este invertirea zaharozei, in care concentratia apei din expresia vitezei de reactie ramane practic constanta si se poate ingloba in valoarea constantei de viteza:
![]()
5. Reactii de ordinul al doilea
Ordinul de reactie este n =
Viteza de reactie este proportionala cu patratul concentratiei unui reactant sau cu produsul concentratiilor a doi reactanti.
O reactie de ordinul al doilea se reprezinta schematic astfel:
a) aA → Produsi
b) aA + bB → Produsi
Viteza de reactie este:
![]() pentru cazul 39a (40)
pentru cazul 39a (40)
respectiv
![]() pentru cazul 39b (41)
pentru cazul 39b (41)
Daca
![]() , ecuatia
(41) devine ecuatia (40).
, ecuatia
(41) devine ecuatia (40).
Se considera cazul 39a.
Considerand ca volumul sistemului este constant, viteza se poate defini in raport cu concentratia cA sau variabila de conversie x. Ecuatiile cinetice diferentiale sunt de forma:
![]() (42)
(42)
respectiv
![]() (43)
(43)
Se
separa variabilele si se integreaza ecuatia (42) intre limitele ![]() cA, respectiv 0, t:
cA, respectiv 0, t:
![]()
Rezulta ecuatia cinetica integrata a reactiei de ordinul al doilea:
![]() (45)
(45)
In ecuatia (43) se separa variabilele si se integreaza intre limitele 0, x, respectiv 0, t:
![]()
Se obtine ecuatia cinetica integrata care contine variabila de conversie x:
![]() (47)
(47)
sau ![]() (48)
(48)
Rezulta: ![]() (49)
(49)
Din ecuatia cinetica integrata (45) rezulta constanta de viteza k:
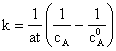 (50)
(50)
Se observa din ecuatia (50) ca dimensiunile constantei de viteza sunt [conc]-1[timp]-1, adica lmol-1s-1.
Ecuatia (45) se poate scrie si sub forma:
![]() (51)
(51)
Reprezentand
grafic ![]() in functie de t (fig. 2) se
obtine o dreapta care are panta egala cu ak si care permite determinarea
constantei de viteza.
in functie de t (fig. 2) se
obtine o dreapta care are panta egala cu ak si care permite determinarea
constantei de viteza.
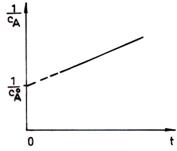
Fig. Liniarizarea ecuatiei cinetice integrate pentru reactia
de ordinul al doilea cu reactanti in concentratii
stoechiometrice
Daca
se pune conditia ![]() in ecuatia (45), se obtine
valoarea timpului de injumatatire:
in ecuatia (45), se obtine
valoarea timpului de injumatatire:
![]() (52)
(52)
care depinde de concentratia initiala a reactantului.
Se considera cazul 39b in care reactantii sunt in concentratii nestoechiometrice. Ecuatiile cinetice diferentiale sunt de forma:
![]() (53)
(53)
respectiv
![]() (54)
(54)
Separarea variabilelor in ecuatia diferentiala (54) si integrarea acesteia duce la ecuatia cinetica integrata de ordinul al doilea:
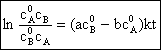
Ecuatia (55) poate fi transpusa in forma liniara:
![]()
Reprezentand
grafic ![]() in functie de timp, se obtine o
dreapta din a carei panta egala cu
in functie de timp, se obtine o
dreapta din a carei panta egala cu ![]() se calculeaza constanta de
viteza de ordinul al doilea (fig. 3.).
se calculeaza constanta de
viteza de ordinul al doilea (fig. 3.).
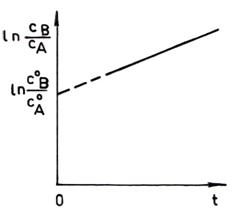
Fig. 3. Liniarizarea ecuatiei cinetice integrate pentru reactia
de ordinul al doilea cu reactanti in concentratii
nestoechiometrice
Reactii de ordinul al doilea sunt descompunerea acidului iodhidric, reactiile de esterificare ale alcoolilor, saponificarea esterilor, formarea sarurilor cuaternare de amoniu:
2HI ![]() H2 + I2
H2 + I2
RCOOH +
R'OH ![]() RCOOR' + H2O
RCOOR' + H2O
RCOOR'
+ OH- ![]() RCOO- + R'OH
RCOO- + R'OH
R3N
+ RX ![]() R4N+X-
R4N+X-
5.3. Reactii de ordinul al treilea
Exista mai multe posibilitati de reactie, cu o singura specie, doua sau trei specii reactante, in care viteza se exprima dupa o cinetica de ordinul al treilea. Reactiile decurg dupa urmatoarele scheme:
a) aA → Produsi
b) aA + bB → Produsi (57)
c) aA + bB + cC → Produsi
In fiecare caz, viteza de reactie se exprima prin urmatoarele ecuatii cinetice diferentiale:
Cazul 57a ![]() (58)
(58)
![]() (59)
(59)
Cazul 57b ![]() (60)
(60)
![]()
Cazul 57c ![]() (62)
(62)
![]()
Integrarea ecuatiei cinetice diferentiale corespunzatoare cazului 57a ce corespunde reactiei unui singur reactant sau a trei reactanti in concentratii stoechiometrice, este cea mai simpla. Ecuatia cinetica integrata de ordinul al treilea este:
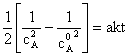 (64)
(64)
Reactiile oxidului de azot cu oxigenul, halogenii sau hidrogenul sunt de ordinul al treilea.
6. CINETICA FORMALA A REACTIILOR COMPLEXE
Cele mai multe reactii chimice din natura sau industrie nu au loc intr-o singura etapa, ci cuprind mai multe etape. Ecuatiile de viteza pentru aceste reactii complexe sau multiple contin mai multe constante de viteza.
6.1. Reactii reversibile (opuse)
Sunt cunoscute numeroase reactii in care reactantii nu se consuma in intregime, instalandu-se un echilibru cand reactia dintre reactantii directi este limitata de reactia dintre produsii de reactie cu reformarea reactantilor initiali. Dintre aceste reactii pot fi amintite reactia de formare a acidului iodhidric, a amoniacului, reactiile de izomerizare.
Reactiile opuse pot avea ordine de reactie diferite.
Pentru discutie se considera ca reactia elementara este de ordinul intai in ambele sensuri, fiind de tipul:
A ![]() B (65)
B (65)
unde: k1 = constanta de viteza a reactiei directe;
k-1 = constanta de viteza a reactiei inverse.
Viteza globala este data de diferenta celor doua viteze de reactie in sens direct si opus prin ecuatia cinetica diferentiala:
![]() (66)
(66)
respectiv
![]() (67)
(67)
La atingerea starii de echilibru, vitezele proceselor in cele doua sensuri ale reactiei sunt egale:
![]()
Rezulta:
![]() (69)
(69)
unde: Kc = constanta de echilibru exprimata prin concentratii;
![]() = concentratiile la echilibru ale lui A,
respectiv B;
= concentratiile la echilibru ale lui A,
respectiv B;
xe = variabila de conversie la echilibru (t = ∞).
Relatia (68) se poate scrie sub forma:
![]() (70)
(70)
Rezulta:
![]() (71)
(71)
Integrarea ecuatiei diferentiale (67) duce la ecuatia cinetica integrata:
![]() (72)
(72)
![]() (73)
(73)
unde: kobs = constanta de viteza observata (experimentala).
6. Reactii paralele
In multe cazuri se obtin alaturi de produsii de reactie doriti si produsi de reactie secundari datorita unor reactii paralele.
Reactiile paralele se clasifica in:
a) reactii paralele gemene
Toti reactantii participa la formarea tuturor produsilor de reactie. De exemplu: nitrarea sau bromurarea fenolului.
Pot fi:
1) reactii paralele gemene de ordinul intai.
Decurg dupa schema:
![]() (74)
(74)
Exemplu: transformari radioactive ale unor nuclee.
2) reactii paralele gemene de ordinul intai cu formarea unui produs de reactie comun
Decurg dupa schema:
![]() (75)
(75)
Exemplu: descompuneri radioactive ale unor nuclee.
3) reactii paralele gemene de ordinul al doilea
Decurg dupa schema:
 (76)
(76)
Exemplu: nitrarea toluenului, halogenarea hidrocarburilor aromatice substituite in nucleul aromatic, halogenarea fenolilor.
b) reactii paralele catalitice
Cand se foloseste un catalizator pentru marirea vitezei de reactie, reactia necatalizata are loc in paralel.
Reactia catalizata si necatalizata decurg dupa schema:
![]() (77)
(77)
unde: C = catalizator.
c) reactii paralele concurente
Din doi sau mai multi reactanti se obtin in mod specific anumiti produsi de reactie, dar numai unii din reactanti participa la toate reactiile.
Se desfasoara dupa schema:
![]() (78)
(78)
Exemplu: reactii de substitutie ale unor complecsi anorganici.
6.1. Reactii paralele gemene de ordinul intai
Schema de reactii elementare:
![]() (74)
(74)
prezinta transformarea unui singur reactant A pe doua cai paralele si independente in doi produsi de reactie.
Viteza globala este suma vitezelor celor doua reactii:
![]() (79)
(79)
Relatia intre viteza de consum a reactantului A si cele de formare a produsilor P si R este:
![]()
sau
![]()
Ecuatia (81) reprezinta ecuatia cinetica diferentiala pentru reactii paralele gemene de ordinul intai.
Constanta de viteza observata este suma constantelor de viteza pentru cele doua reactii:
kobs = k1 + k2 (82)
Integrarea ecuatiei (81) duce la:
![]()
respectiv
![]() (84)
(84)
Raportul vitezelor de formare a produsilor de reactie este:
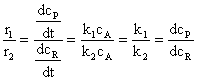 (85)
(85)
respectiv
![]()
Intrucat ![]() se obtine:
se obtine:
![]() (87)
(87)
Conform relatiei (87) se constata ca daca reactiile paralele gemene sunt de acelasi ordin, raportul concentratiei produsilor de reactie este egal cu raportul constantelor de viteza individuale si este independent de timp. Raportul concentratiei produsilor de reactie numit factor de selectivitate se poate modifica in scopul obtinerii produsului dorit in concentratie mai mare, daca se modifica temperatura.
6. Reactii paralele gemene de ordinul intai cu formarea unui produs de reactie comun
Se desfasoara dupa schema:
![]() (75)
(75)
Ecuatiile de viteza pentru reactiile paralele sunt:
![]()
![]()
Relatia intre vitezele de consum a reactantilor si cea de formare a produsului de reactie este:
![]() (90)
(90)
sau
![]() (91)
(91)
Integrarea ecuatiilor cinetice diferentiale (88) si (89) duce la:
![]() (92)
(92)
si
![]() (93)
(93)
Ecuatia cinetica diferentiala (91) poate fi scrisa sub forma:
![]() (94)
(94)
Prin integrarea ecuatiei diferentiale (94) rezulta:
![]()
6.3. Reactii paralele gemene de ordinul al doilea
Reactiile pot fi reprezentate dupa schema:
 (76)
(76)
Legea de viteza este descrisa de ecuatia cinetica diferentiala:
![]()
Daca cA = cB atunci prin integrarea ecuatiei diferentiale (96) se obtine ecuatia cinetica integrata de ordinul al doilea:
![]() (97)
(97)
unde: kobs = k1 + k2 + k3 (98)
Daca reactantii sunt in concentratii nestoechiometrice, ecuatia cinetica integrata de ordinul al doilea este de forma:
![]() (99)
(99)
Raportul vitezelor de formare a produsilor de reactie dau factorii de selectivitate conform relatiilor:
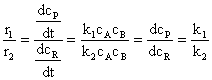 (100)
(100)
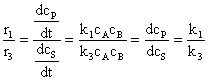 (101)
(101)
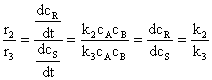 (102)
(102)
Deoarece
![]() ,
relatiile (100), (101) si (102) devin:
,
relatiile (100), (101) si (102) devin:
![]() (103)
(103)
![]() (104)
(104)
![]() (105)
(105)
6.4. Reactii paralele. O reactie catalizata si alta necatalizata
Reactia catalizata decurge in paralel cu reactia necatalizata conform schemei:
![]() (77)
(77)
unde: ![]() =
constanta de viteza in absenta catalizatorului;
=
constanta de viteza in absenta catalizatorului;
![]() = constanta de viteza in prezenta catalizatorului.
= constanta de viteza in prezenta catalizatorului.
Viteza globala a procesului exprimata fie prin disparitia reactantului A, fie prin aparitia produsului de reactie P este:
![]() (106)
(106)
sau
![]() (107)
(107)
unde: kobs
= ![]() (108)
(108)
Concentratia catalizatorului cC este constanta.
Integrand ecuatia cinetica diferentiala (107) se obtine:
![]() (109)
(109)
Desi reactia catalizata urmeaza o cinetica de ordinul al doilea, procesul global este de ordinul intai.
Prin reprezentarea grafica a constantei de viteza observate in functie de concentratia de catalizator (ecuatia 108) se obtine o dreapta a carei parametrii permit determinarea constantelor de viteza individuale pentru reactia catalizata si cea necatalizata.
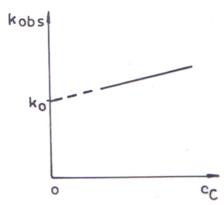
Fig. 4. Dependenta liniara a constantei de viteza observate de
concentratia de catalizator
6.5. Reactii paralele concurente
Aceste reactii au loc dupa schema:
![]() (78)
(78)
Vitezele celor doua reactii sunt date de legea vitezei :
![]() (110)
(110)
respectiv
![]() (111)
(111)
Viteza globala sau viteza de transformare a reactantului A este:
![]() (112)
(112)
Exista urmatoarele situatii:
1) Daca reactantii B si C se afla in exces fata de A, adica cB >> cA si cC >>cA atunci ecuatia diferentiala (112) devine:
![]() (113)
(113)
Concentratiile cB si cC raman practic constante in timpul reactiei si pot fi inglobate in constantele de viteza individuale.
Ecuatia (113) este asemanatoare ecuatiei diferentiale (81) de la reactii paralele gemene de ordinul intai.
2) Daca reactantul A este in exces atunci reactiile paralele concurente se vor comporta ca reactii independente, avand ecuatiile de viteza de forma:
![]() (114)
(114)
![]() (115)
(115)
deoarece cA este considerata constanta.
6.3. Reactii succesive sau consecutive
Sunt procese in care produsul de reactie al unei etape este reactant pentru urmatoarea etapa.
Reactiile succesive se caracterizeaza prin formarea unor intermediari reactivi inainte de formarea produsului final.
Aceste reactii pot fi exemplificate prin dezintegrari ale elementelor radioactive, hidrolize succesive, aditie de apa la nitrili, substitutii in nucleul benzenic.
Cea mai frecventa succesiune de reactii este cea formata din doua reactii de ordinul intai ireversibile dupa schema:
![]()
Ecuatiile cinetice diferentiale care descriu variatia concentratiilor in timp sunt:
![]() (117)
(117)
![]() (118)
(118)
![]() (119)
(119)
Prin integrarea ecuatiei (117) se obtine:
![]() (120)
(120)
Prin rearanjarea ecuatiei (118) si substitutia lui cA, rezulta:
![]() (121)
(121)
Evolutia concentratiei intermediarului cB cu timpul se obtine prin rezolvarea ecuatiei diferentiale (121):
![]() (122)
(122)
Concentratia lui C se poate obtine din bilantul de concentratii:
![]() (123)
(123)
Substitutia lui cA si cB in acest bilant si rearanjarea ecuatiei (123) duce la:
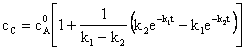 (124)
(124)
Fig. 5. prezinta reprezentarea concentratiilor speciilor A, B si C in functie de timp, descrise de ecuatiile (120), (122) si (124).
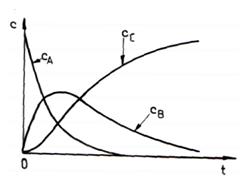
Fig. 5. Curbele cinetice ale unei succesiuni de doua reactii
de ordinul intai
Ecuatia (124) are doua cazuri limita:
a)
Daca k1 >> k2,
intermediarul se formeaza rapid si dispare lent. In ecuatia (124) se neglijeaza
termenul ![]() in comparatie cu
in comparatie cu ![]() si k2 fata de k1,
reducandu-se la:
si k2 fata de k1,
reducandu-se la:
![]() (125)
(125)
Viteza de obtinere a produsului final C depinde numai de etapa a doua care este mai lenta. Aceasta etapa se numeste etapa determinanta de viteza.
b) Daca k2 >> k1, intermediarul este foarte reactiv si se consuma, avand o concentratie maxima foarte scazuta. Aceasta concentratie se mentine aproape constanta pe un interval de timp mare. Ecuatia (124) devine:
![]() (126)
(126)
Viteza globala este determinata de prima etapa care este lenta. Intermediarul se formeaza lent si se consuma in ritmul in care se formeaza. Concentratia intermediarului este practic stationara si se poate considera ca viteza sa de acumulare este zero, adica:
![]() (127)
(127)
sau
![]() (128)
(128)
Rezulta:
![]() (129)
(129)
Acest caz limita in care viteza de transformare a intermediarului reactiv este nula se numeste aproximatia starii stationare.
Substituind valoarea lui cB data de relatia (129) in ecuatia (119), aceasta devine:
![]() (130)
(130)
Integrarea ecuatiei (130) duce la ecuatia (126) corespunzatoare cazului limita k2 >> k1.
7. FACTORII CARE INFLUENTEAZA VITEZA DE REACTIE
7.1. Influenta concentratiei reactantilor
Dependenta vitezei de reactie de concentratia reactantilor este exprimata prin legea vitezei sau legea cinetica a actiunii maselor (18).
7. Influenta temperaturii
Pentru cele mai multe reactii chimice, viteza de reactie se modifica cu cresterea temperaturii. Examinand legea vitezei se constata ca temperatura nu are influenta asupra concentratiei reactantilor, ci asupra constantei de viteza.
Primul care a incercat pe cale empirica sa exprime dependenta constantei de viteza de temperatura a fost J. J. Hood si apoi van't Hoff sub forma ecuatiei:
![]()
unde: A, B = constante independente de temperatura.
Nu toate ciocnirile dintre particulele reactante sunt eficace astfel incat sa conduca la produsii de reactie. Daca energia cinetica a particulelor care se ciocnesc depaseste o anumita energie de activare, reactia se produce, iar particulele care satisfac aceasta conditie sunt activate , suferind ciocniri eficace.
Deci energia de activare reprezinta energia cinetica minima pe care trebuie sa o posede particulele reactante in momentul ciocnirii pentru a realiza reactia chimica.
Cresterea
temperaturii produce o crestere a energiei cinetice. Numarul ciocnirilor
eficace dintre particulele care ating energia de activare creste in unitatea de
timp. ceea ce duce la cresterea vitezei de reactie. Fractia de ciocniri eficace
este data de moleculele ce vor avea o energie cinetica mai mare decat energia
de activare si este proportionala cu factorul lui Boltzmann: ![]() .
.
Dependenta acestei constante de viteza de temperatura este data de ecuatia Arrhenius:
![]() (132)
(132)
unde: A = factor preexponential (factor de frecventa): constanta caracteristica reactiei chimice data de fractia de ciocniri eficace;
Ea = energie de activare;
R = constanta generala a gazelor;
T = temperatura absoluta.
Ecuatia Arrhenius (132) poate fi scrisa sub forma logaritmica:
![]() (133)
(133)
Constanta de viteza k este cu atat mai mare cu cat A este mai mare si cu cat Ea este mai mica.
Se considera ca reactia chimica este la echilibru.
Constanta de echilibru Kc este raportul constantelor de viteza ale reactiei directe (k1) si ale reactiei inverse (k2):
Kc = k1/k (relatia 69)
Influenta temperaturii asupra constantei de echilibru Kc este data de izocora de reactie a lui van't Hoff (volumul 1):
![]()
Entalpia
de reactie ![]() este diferenta celor doua energii de activare
care caracterizeaza reactia directa si reactia inversa:
este diferenta celor doua energii de activare
care caracterizeaza reactia directa si reactia inversa:
![]()
unde: E1 = energia de activare a reactiei directe;
E2 = energia de activare a reactiei indirecte.
Substituind
Kc si ![]() in izocora de reactie a lui van't Hoff
rezulta:
in izocora de reactie a lui van't Hoff
rezulta:
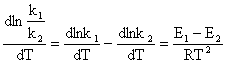
Relatia (135) se poate scrie sub forma:
![]() (136.a)
(136.a)
si
![]() (136.b)
(136.b)
Relatiile (136.a) si (136.b) sunt valabile pentru orice temperatura daca constanta din membrul al doilea este nula.
Prin derivarea ecuatiei Arrhenius (133) in raport cu temperatura se obtine:
![]()
Deci ecuatiile (136.a) si (136.b) sunt identice cu ecuatia Arrhenius in forma derivata (137).
In fig. 6. este prezentata diagrama energetica calitativa pentru o reactie chimica exoterma la echilibru:
A + B ![]() Produsi.
Produsi.
Indiferent de sensul reactiei chimice, intre reactanti si produsi exista o bariera energetica care trebuie invinsa pentru a se produce transformarea in sens direct sau in sens invers.
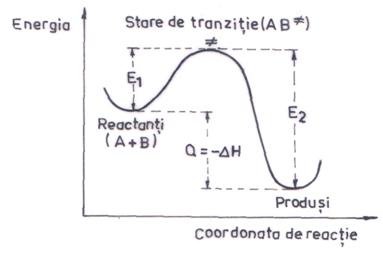
Fig. 6. Diagrama energetica a reactiei chimice:
Reactanti ![]() Produsi
Produsi
Teoria complexului activat sau a starii de tranzitie postuleaza formarea unui complex activat sau stare de tranzitie care exista in trecerea de la starea de reactanti la cea de produsi de reactie (fig. 6.).
Energia complexului activat este cea mai mare pe aceasta cale, fiind in maximul curbei energetice care leaga reactantii de produsi. De asemenea, s-a postulat ca complexul activat se afla in echilibru cu reactantii.
Calea de energie minima se numeste coordonata de reactie.
O reactie elementara are un singur complex activat. Daca exista un set de reactii elementare care formeaza un mecanism complex, atunci fiecare etapa elementara are complexul activat propriu.
7.1. Determinarea energiei de activare
a) Metoda grafica
Se determina constantele de viteza la cateva temperaturi si se reprezinta grafic lnk in functie de 1/T (fig. 7). Ecuatia (133) arata ca reprezentarea grafica este o dreapta a carei panta permite determinarea energiei de activare, iar ordonata la origine furnizeaza factorul de frecventa A.
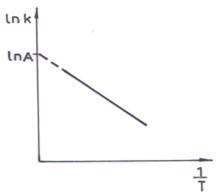
Fig. 7. Reprezentarea ecuatiei Arrhenius in forma
logaritmica pentru calculul energiei de activare
si a factorului de frecventa.
b) Metoda analitica
Se determina constanta de viteza pentru doua temperaturi si se scrie forma logaritmica a ecuatiei Arrhenius:
![]() (138)
(138)
![]() (139)
(139)
Prin scadere se obtine:
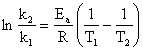 (140)
(140)
Din relatia (140) rezulta energia de activare:
![]() (141)
(141)
Acest calcul se efectueaza pentru mai multe valori ale temperaturii, obtinandu-se aceeasi valoare pentru energia de activare.
7.3. Influenta presiunii
Cand reactantii sunt in stare gazoasa, viteza de reactie este influentata de presiune intrucat concentratia este direct proportionala cu aceasta: p = cRT.
7.4. Influenta suprafetei de contact
Suprafata de contact este un factor care influenteaza viteza reactiilor chimice eterogene.
Se considera pentru exemplificare reactia:
Pb(NO3)2 + 2KI à PbI2↓ + 2KNO3
pp galben
Se constata ca reactia are loc practic instantaneu in solutie si cu viteza mica in amestecul pulverulent. Cand reactantii sunt sub forma de cristale, viteza reactiei este mai mica decat cazurile anterioare.
Numarul punctelor de contact care se stabilesc intre granulele reactantilor solizi este mai mare cand acestia au diametrul particulelor mai mic (grad de dispersie mai mare).
In sistemele eterogene, desfasurarea reactiei este favorizata de existenta unor suprafete de contact mari.
7.5. Influenta catalizatorilor
Notiunea de catalizator a fost introdusa de J.J. Berzelius (1836).
Catalizatorul este o substanta care participa la reactia chimica si ramane netransformat din punct de vedere chimic dupa reactie.
Catalizatorul
mareste viteza reactiei chimice termodinamic posibile (![]() ).
).
Energia de activare a reactiei necatalizate este mai mare decat a celei catalizate. Acest fapt este ilustrat in fig. 8..
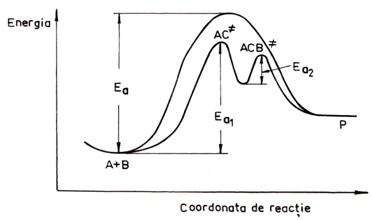
Fig. 8. Diagrama energetica a reactiei necatalizate si a
reactiei catalizate
Reactia necatalizata: A + B à P Ea
Reactia catalizata: A + C à
AC ![]()
(142)
AC
+ B à P + C ![]()
unde: C = catalizator.
In cazul reactiilor de echilibru, catalizatorul modifica in egala masura atat viteza reactiei directe cat si a celei opuse deoarece nu modifica constanta de echilibru data de raportul celor doua constante de viteza.
8. CATALIZA
Prin cataliza se intelege fenomenul de modificare a vitezei de reactie in urma folosirii catalizatorului.
Cataliza poate fi omogena cand reactantii si catalizatorul se gasesc in aceeasi faza sau eterogena cand catalizatorul se afla in alta faza.
Daca reactia chimica este catalizata de enzime, cataliza este enzimatica.
Enzimele sunt macromolecule cu structura complexa care catalizeaza reactiile biochimice din organismele vii (oxidare, reducere, hidroliza). Enzimele sunt catalizatori deosebit de eficienti pentru o mare varietate de reactii de importanta biologica.
8.1. Cataliza omogena
Catalizatorul si reactantii se gasesc in aceeasi faza fluida. Catalizatorul participa direct in mecanismul de reactie. Exemple de cataliza omogena sunt date de cataliza cu acizi si baze si cataliza cu complecsi metalici.
Mecanismul cel mai frecvent intalnit implica formarea unui complex intermediar intre catalizator si unul din reactanti numit substrat care apoi se descompune, formand produsii de reactie. Daca intervine un al doilea reactant, acesta va interactiona cu intermediarul. Mecanismul a fost formulat de Laidler (1950):
 (143)
(143)
unde: S = substrat;
C = catalizator;
X = complex intermediar intre substrat si catalizator;
R = al doilea reactant;
P = produs de reactie;
Y = produs (in multe reactii nu apare).
Aceasta succesiune de reactii elementare se numeste mecanism de activare asociativa a substratului.
In cataliza cu ioni metalici, in special in cea redox, exista situatii cand X nu este un complex intermediar intre catalizator si substrat, ci o forma modificata a catalizatorului (o alta stare de valenta). Aceasta interactioneaza cu reactantul R spre a regenera catalizatorul C si produsul de reactie. Acest tip de mecanism mediat de catalizator se numeste mecanism de activare neasociativa a substratului.
Privind varianta activarii asociative exista doua posibilitati:
1) Formarea complexului intermediar are loc rapid, iar reactia lui cu reactantul R este lenta, fiind etapa determinanta de viteza. Daca se indeplineste conditia k1, k-1 >> k2, formarea intermediarului este un preechilibru, iar concentratia sa se poate obtine din constanta de echilibru:
![]() (144)
(144)
Concentratia
totala de catalizator (![]() ) este
egala cu suma dintre concentratia catalizatorului in stare libera (
) este
egala cu suma dintre concentratia catalizatorului in stare libera (![]() ) si cea a
complexului intermediar (cX):
) si cea a
complexului intermediar (cX):
![]()
Rezulta concentratia catalizatorului in stare libera din relatia (145):
![]()
Inlocuind
![]() in relatia (144), se obtine concentratia
complexului intermediar X:
in relatia (144), se obtine concentratia
complexului intermediar X:
![]()
Rezulta:
![]() (148)
(148)
Legea de viteza este:
![]() (149)
(149)
De regula, k1 << k-1 si constanta de echilibru Kc are o valoare mica. Prin neglijarea termenului KccS de la numitorul ecuatiei (149), viteza de reactie devine:
![]() (150)
(150)
Daca Y nu apare in mecanism atunci legea de viteza este de forma:
![]() (151)
(151)
si prezinta ordinul intai in raport cu catalizatorul, substratul si respectiv reactantul.
2) Daca k2 >> k1, k-1 atunci complexul intermediar este foarte reactiv, iar concentratia sa este constanta si se poate aplica metoda starii stationare. In acest caz formarea complexului intermediar este lenta si este etapa determinanta de viteza. Viteza de transformare a lui X este:
![]() (152)
(152)
Substituind
![]() data de relatia (146), ecuatia (152) devine:
data de relatia (146), ecuatia (152) devine:
![]() (153)
(153)
Rezulta concentratia complexului intermediar:
![]() (154)
(154)
Viteza de formare a produsului de reactie este:
![]() (155)
(155)
Ecuatia (155) prezinta doua cazuri limita:
a) k2 >> k1, k-1
Legea de viteza devine:
![]() (156)
(156)
Se observa ca viteza de reactie nu depinde de concentratia reactantului R, dar depinde de concentratia catalizatorului. Formarea complexului intermediar este etapa lenta care determina viteza procesului, iar transformarea sa in produs de reactie este rapida. Intermediarul de acest tip se numeste intermediar van't Hoff.
Un exemplu il constituie halogenarea cetonelor in cataliza acida.
b) k1, k-1 >> k2
Legea de viteza devine:
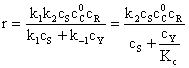
Deoarece k1 <<k-1, Kc are o valoare mica, iar termenul cS se poate neglija la numitorul ecuatiei (157) care devine ecuatia (150) corespunzatoare unui preechilibru.
Formarea intermediarului este rapida, iar transformarea sa in produs de reactie este etapa determinanta de viteza, adica etapa lenta. Intregul proces poate fi tratat ca o reactie cu preechilibru, iar intermediarul este de tip Arhenius. Viteza de reactie depinde de concentratia catalizatorului.
Un exemplu il reprezinta reactiile de hidroliza catalizate de acizi.
8. Cataliza enzimatica
Enzimele sunt substante macromoleculare de natura proteica cu mase moleculare in domeniul 105 - 107 g/mol. Ele catalizeaza o varietate mare de tipuri de reactii, avand ca substrat de la molecule mici la macromolecule, cum sunt proteinele. Se clasifica in enzime hidrolitice, oxidoreducatoare, de transfer, de aditie si de izomerizare.
Enzimele se caracterizeaza printr-o eficienta si specificitate mare, iar actiunea lor prezinta o dependenta pronuntata de pH.
Se considera ca o parte anume din macromolecula enzima numita centru activ care este polifunctional, are rol determinant in procesul catalitic.
Enzimele se folosesc in industria alimentara si in industria farmaceutica. In industria alimentara enzimele se utilizeaza la obtinerea berii, vinului, painii, glucozei. In prezenta enzimelor are loc scindarea unor molecule precum: zaharoza in glucoza si fructoza, lactoza in glucoza si galactoza.
Enzimele sunt catalizatori atat de eficienti incat au actiune importanta chiar la concentratii foarte mici: 10-10 - 10-8 mol/l. Domeniul de concentratii de substrat este 10-6 - 10-3 mol/l. In asemenea conditii, intermediarii de reactie sunt intr-o concentratie mult mai mica decat a substratului. Dupa o perioada de timp mica de la declansarea reactiei enzimatice, intermediarii pot fi considerati ca atingand o concentratie stationara.
Cinetica reactiilor enzimatice a fost explicata de catre Michaelis si Menten care au folosit aproximatia starii stationare. Ei au propus urmatorul mecanism:
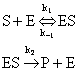 (158)
(158)
unde: S = substrat;
P = produs de reactie;
E = enzima;
ES = intermediar sau complex enzima-substrat.
Intermediarul ES are o concentratie constanta, atingand starea stationara, adica:
![]() (159)
(159)
Rezulta concentratia intermediarului ES:
![]() (160)
(160)
Folosind relatia:
![]() (161)
(161)
unde: ![]() =
concentratia totala a enzimei;
=
concentratia totala a enzimei;
cE = concentratia enzimei in stare libera.
expresia (160) devine:
![]()
Se obtine:
![]() (163)
(163)
Viteza de formare a produsului este:
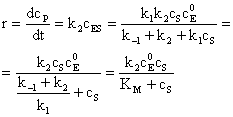 (164)
(164)
unde: 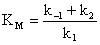 (165)
(165)
KM se numeste constanta Michaelis pentru substrat.
Legea de viteza (164) prezinta doua situatii limita:
a) Daca cS >>KM, legea de viteza devine:
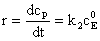 (166)
(166)
Ordinul de reactie in raport cu substratul este zero.
Viteza de reactie este constanta daca concentratia substratului este foarte mare.
Etapa
determinanta de viteza este descompunerea complexului enzima-substrat in
produsul de reactie. Constanta de viteza k2 se numeste numarul de
ciclu (turnovernumber) si reprezinta repetabilitatea actului catalitic in
unitatea de timp. Produsul ![]() reprezinta viteza maxima a reactiei enzimatice,
fiind proportionala cu concentratia totala de enzima. Dependenta vitezei de
reactie de concentratia substratului este prezentata in fig. 9.
reprezinta viteza maxima a reactiei enzimatice,
fiind proportionala cu concentratia totala de enzima. Dependenta vitezei de
reactie de concentratia substratului este prezentata in fig. 9.

Fig. 9. Dependenta vitezei de reactie de concentratia
de substrat la concentratie de enzima constanta
b) Daca cS << KM, legea de viteza devine:
![]() (167)
(167)
Viteza de reactie este proportionala cu concentratia de substrat si cu concentratia totala de enzima.
In general in mecanismul reactiilor enzimatice apar mai multi intermediari pentru care se aplica aproximatia starii stationare, iar forma ecuatiei de viteza nu se schimba.
9. APLICATII NUMERICE
1) Reactia de ordinul intai de descompunere in faza gazoasa a bromurii de etil are loc la temperatura de 450C. Stiind ca concentratia initiala a bromurii de etil este de 1,08510-2 molil-1, sa se determine viteza de reactie dupa 10 minute, daca in acest moment 45,5% din cantitatea initiala de reactant a trecut in produsi de reactie.
Rezolvare:
C2H5Br à C2H4 + HBr
c
= ![]() - x
- x
c
= ![]() -
- ![]() c0
= 0,545
c0
= 0,545 ![]()
![]()
=>
![]()
r = kc = 1,01 10-3 0,545 1,805 10-2
r = 9,935 10-6 moll-1s-1
2) Pentru o reactie de ordinul intai, constanta de viteza functie de temperatura are urmatoarele valori:
pentru 0C k1 = 10-5 s-1;
pentru 45C k2 = 310-3 s-1.
Considerand concentratia initiala egala cu 0,1 moll-1 si temperatura de 25C, sa se calculeze viteza de reactie dupa 3000 s.
Rezolvare:
lnk1
= lnA - ![]()
lnk2
= lnA - ![]()
=>
![]()
Ea = 9,15104 Jmol-1
lnk1
= lnA - ![]()
=>
lnA = lnk1 + ![]()
![]()
k3 = constanta de viteza la 25C
lnk3 = lnA - ![]()
![]()
k3 = 3,24 10-4 s-1
![]()
![]()
r = 1,37 10-5 moll-1s-1
3) Viteza reactiei A à Produsi are valoarea 3,810-4 moll-1s-1 cand cA = 0,2 moll-1 si 9,510-4 moll-1s-1 cand cA = 0,5 moll-1. Sa se calculeze ordinul reactiei si constanta de viteza.
Rezolvare:
![]()
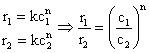
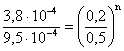 =>
=>
2,5 = (2,5)n => n = 1 =>
r1
= kc1 => ![]()
![]()
4) Descompunerea in faza gazoasa, conform reactiei:
CH3CHO à CH4 + CO
este o reactie de ordinul al doilea in raport cu aldehida acetica. La 530C, concentratia initiala de aldehida acetica este de 8 moll-1, iar cea finala este de 6 moll-1 dupa 100 secunde.
a) Sa se determine constanta de viteza la 530C.
b) Cunoscand ca energia de activare a reactiei este 1,9105 Jmol-1, sa se calculeze temperatura la care constanta de viteza devine de 10 ori mai mare ca la 530C.
Rezolvare:
a) ![]() =>
=>
![]()
![]()
b) k2 = 10k1
![]()
![]()
=> 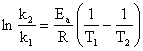
=> 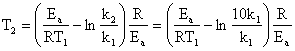
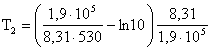
T2 = 873,67 K
5) Reactia A à P este de ordinul al doilea. In momentul initial, viteza de reactie este 10-3 moll-1min-1, iar dupa 60 de minute, viteza de reactie are valoarea 2,510-4 moll-1min-1. Sa se calculeze concentratia initiala a lui A si constanta de viteza.
Rezolvare:
![]() =>
=> ![]()
r = kc2
=> ![]()
![]()
=> ![]() =>
=> ![]()
![]()
=> ![]()
=> ![]()
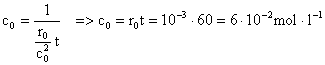
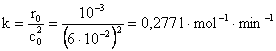
6) Reactia 2A à P este de ordinul al doilea, avand constanta de viteza 3,510-4 lmol-1s-1. Sa se determine timpul necesar ca pentru reactantul A, concentratia sa scada de la 0,260 moll-1 la 0,011 moll-1.
Rezolvare:
![]()
=> 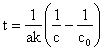
![]()
t = 1,24105 s
7) Constanta de viteza in functie de temperatura pentru reactia de dimerizare a butadienei are valorile:
|
T (K) | ||
|
k (moll-1s-1) |
Sa se determine energia de activare a reactiei.
Rezolvare:
![]()
![]()
=> ![]()
![]()
8) Pentru o reactie de ordinul intai, constantele de viteza au urmatoarele valori:
|
T (K) | ||
|
k (s-1) |
Reactia are loc in doua reactoare, unul functionand la 313 K si celalalt la 333 K. Daca concentratia initiala in al doilea reactor este de 2,72 ori mai mare ca in primul, sa se calculeze timpul dupa care concentratia este egala in cele doua reactoare.
Rezolvare:
![]()
![]()
![]()
![]()
c1 = c2 => ![]()
ln2,72 = (k2 - k1)t
![]()
9) Constanta de viteza la descompunerea de ordinul intai a N2O5 in reactia:
2N2O5 à 4NO2 + O2
este 1,3810-5 s-1 la 25C. Cat este timpul de injumatatire a N2O5?
Rezolvare:
![]()
10) O reactie de ordinul al doilea, de tipul A + B à P, s-a desfasurat intr-o solutie care are concentratia initiala 0,05 moll-1 in A si 0,08 moll-1 in B. Dupa o ora, concentratia lui A a scazut la 0,02 moll-1. Sa se calculeze constanta de viteza.
Rezolvare:
![]()
x = 0,05 - 0,02 = 0,03 ![]()
=> ![]()
![]()
=> ![]()
![]()
11) Reactia A + 2B à P1 + P2 este de ordinul al doilea. Concentratiile initiale sunt 510-3 moll-1 pentru A si 1010-3 moll-1 pentru B. Concentratia de P1 obtinuta dupa 14,6 min a fost de 210-3 moll-1, la 50C. Sa se calculeze constanta de viteza.
Rezolvare:
r = kc1c2
![]()
![]()
![]()
=> ![]()
![]()
=> ![]()
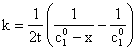
![]()
![]()
12) O substanta A participa la doua reactii paralele de ordinul intai:
![]()
Constantele de viteza depind de temperatura, conform ecuatiilor:
![]()
![]()
a) Sa se calculeze raportul vitezelor de reactie la 800 K.
b) Sa se determine temperatura la care vitezele de reactie devin egale.
Rezolvare:
a) ![]()
![]()
![]()


b) r1 = r2 => k1cA = k2cA
k1 = k2
![]()
![]()
=> ![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 9678
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved