| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Cinetica reactiilor elementare. Efectul concentratiilor
Reactiile elementare reprezinta elementele constitutive ale tuturor transformarilor chimice. Cu rare exceptii, cele mai complexe transformari chimice pot fi reprezentate ca un ansamblu de reactii elementare, monomoleculare si bimoleculare. Uneori se presupune ca pot avea loc si reactii trimoleculare. Dupa cum se va vedea in continuare, o reactie trimoleculara poate fi asimilata, cu o foarte buna aproximatie, cu o succesiune de doua reactii bimoleculare, astfel incat se poate renunta la conceptul de reactie trimoleculara fara a pierde din precizia descrierii cantitative a unui sistem chimic reactant. Reactiile cu o molecularitate superioara nu sunt considerate ca evenimente probabile.
Astfel, elementele constitutive ale oricarei reactii complexe sunt reactiile monomoleculare si cele bimoleculare. Numarul de molecule care participa la o reactie elementara si sufera transformari chimice este numit molecularitate. Trebuie remarcat ca molecularitatea este o notiune conceptuala, bazata pe modelele cinetico-moleculare ale substantelor in diferite stari de agregare. Ea a fost definita la inceput pentru reactiile din faza gazoasa. In sisteme condensate (lichide, sau in stare adsorbita pe o suprafata solida) moleculele reactante sufera numeroase alte ciocniri cu particulele vecine ale solventului sau ale suprafetei solide, dar aceste particule nu sunt luate in consideratie la definirea molecularitatii, atata timp cat ele nu sufera transformari chimice. Cunoasterea comportarii cinetice a reactiilor elementare este indispensabila in analiza evolutiei temporale a sistemelor chimice mai simple sau mai complexe.
Ecuatiile cinetice definite anterior sunt de forma generala:
![]()
unde notatia vR este simbolica; ea
reprezinta de fapt un cat diferential de forma generala: ![]() ,care, pentru o
reactie intr-un sistem omogen avand loc intr-un reactor discontinuu cu
volum constant, devine:
,care, pentru o
reactie intr-un sistem omogen avand loc intr-un reactor discontinuu cu
volum constant, devine: 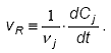
Ecuatii cinetice diferentiale
Se vede ca ecuatia cinetica in care variabila dependenta este o viteza de reactie este o ecuatie diferentiala. Vom discuta in continuare ecuatiile cinetice diferentiale pentru reactiile elementare in sisteme omogene la volum constant. Aceste ecuatii pot fi extinse fara dificultate si pentru alte conditii. Ecuatiile cinetice sunt dependente atat de concentratii, prin functia f Cj , cat si de temperatura prin constanta de viteza k. Pentru inceput vom analiza dependenta de concentratie.
Reactii monomoleculare
Reactii monomoleculare de forma A produsi (produsii posibili sunt de forma B, 2B, B + C)
Ecuatia cinetica diferentiala este de forma:
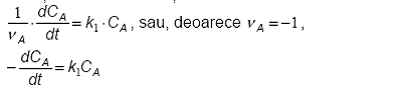 (42)
(42)
Reactii bimoleculare monocomponente
Reactii bimoleculare de forma 2A produsi (reactie bimoleculara monocomponenta)
Ecuatia cinetica diferentiala este de forma:
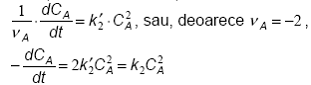 (43)
(43)
Reactii bimoleculare bicomponente
Reactii bimoleculare de forma A + B produsi (reactie bimoleculara bicomponenta)
Ecuatia cinetica diferentiala este de forma:
![]() (44)
(44)
Ultima ecuatie contine, aparent, doua variabile de
compozitie (doua concentratii, CA si CB). In realitate, cele
doua variabile nu sunt independente, dupa cum se poate vedea din
relatia de definitie a avansarii reactiei![]() , de unde
rezulta
, de unde
rezulta![]() . Ecuatia
cinetica (44) ia forma:
. Ecuatia
cinetica (44) ia forma:
![]() (44
(44
Printr-un procedeu analog, ecuatiile ( 42) si (43) iau formele:
![]() (42
(42
![]() (43
(43
Constantele de viteza pentru procesele monomoleculare au fost notate cu indicele 1, iar pentru cele bimoleculare cu 2. In continuare nu se va mai face aceasta distinctie, apartenenta la unul din cele doua procese elementare rezultand din forma ecuatiei stoichiometrice.
Se observa ca ecuatiile cinetice diferentiale, caracteristice celor trei tipuri de reactii elementare, respecta legea actiunii maselor. Aceasta comportare este specifica numai reactiilor elementare.
Prin extensie, se pot deduce si ecuatiile cinetice diferentiale pentru ipoteticele reactii trimoleculare.
Din formele ecuatiilor cinetice diferentiale ale reactiilor elementare se observa ca viteza de reactie depinde numai de concentratiile componentilor reactanti si este independenta de concentratiile produsilor de reactie. O astfel de comportare este caracteristica sistemelor ideale, in care interactiile dintre moleculele componentilor sunt neglijabile. In sistemele reale, in care natura mediului (solventul, taria ionica etc.) se schimba semnificativ odata cu avansarea reactiei, acumularea produsilor de reactie poate influenta sensibil viteza reactiei (efectul de feedback).
Forma ecuatiilor cinetice diferentiale este cunoscuta numai pentru reactiile elementare. Pentru reactiile complexe, aceasta forma poate fi gasita numai pe cale experimentala. Legea actiunii maselor nu poate fi aplicata reactiilor complexe.
Fiecare ecuatie cinetica discutata contine cate un parametru caracteristic, numit in acest caz constanta de viteza. Constantele de viteza reflecta specificul fiecarei reactii elementare si depind de caracteristicile structurale ale reactantilor. Asa cum s-a precizat mai sus, constantele de viteza sunt dependente de temperatura. Pentru multe dintre sistemele reale, constantele de viteza depind si de natura mediului.
Utilitatea ecuatiilor cinetice diferentiale in studiul evolutiei temporale a sistemelor chimice reactante
Ecuatiile cinetice diferentiale ale reactiilor elementare pot fi utilizate
pentru:
![]() evaluarea constantelor de viteza din curbele
cinetice experimentale
evaluarea constantelor de viteza din curbele
cinetice experimentale
![]() simularea evolutiei temporale a unei
reactii elementare atunci cand se cunoaste constanta de viteza
si compozitia initiala
simularea evolutiei temporale a unei
reactii elementare atunci cand se cunoaste constanta de viteza
si compozitia initiala
![]() descrierea evolutiei temporale a
reactiilor complexe ca rezultat al cuplarii reactiilor
elementare
descrierea evolutiei temporale a
reactiilor complexe ca rezultat al cuplarii reactiilor
elementare
Evaluarea constantelor de viteza
Vom discuta pentru inceput procedeul de evaluare a constantelor de viteza din curbele cinetice experimentale. Presupunem ca am obtinut curba Cj F t , fie ca o curba continua, fie ca o succesiune de perechi concentratie - timp. Conform relatiei de definitie a avansarii reactiei, se poate construi si curba l j t , din care, prin derivare, se obtin vitezele dl dt , corespunzatoare fiecarei valori a avansarii reactiei.
Reprezentarile grafice (sau analiza
statistica cu ajutorul metodei de regresie liniara) ) dl dt in functie de ![]() pentru reactiile
monomoleculare, sau in functie de
pentru reactiile
monomoleculare, sau in functie de ![]() pentru reactiile bimoleculare monocomponente, sau in
functie de
pentru reactiile bimoleculare monocomponente, sau in
functie de ![]() pentru reactiile
bimoleculare bicomponente, dau posibilitatea evaluarii grafice sau
statistice a constantelor de viteza.
pentru reactiile
bimoleculare bicomponente, dau posibilitatea evaluarii grafice sau
statistice a constantelor de viteza.
Celelalte doua aplicatii ale ecuatiilor cinetice diferentiale vor fi discutate in capitolele care urmeaza.
Dimensiuni ale constantelor de viteza
Analiza dimensionala a ecuatiilor cinetice si utilizarea probabilitatii de reactie
Conform definitiei, viteza de reactie ![]() , sau dl dt se exprima in
, sau dl dt se exprima in ![]() Daca reactia are loc pe o suprafata,
unitatea de masura este
Daca reactia are loc pe o suprafata,
unitatea de masura este ![]() . Dimensiunile constantelor
de viteza rezulta din ecuatia cinetica:
. Dimensiunile constantelor
de viteza rezulta din ecuatia cinetica:
o pentru reactii monomoleculare <k> = s-1 si are deci semnificatia unei frecvente
o pentru reactii bimoleculare <k> = L mol-1 s-1, sau m2 mol-1 s-1 pentru reactii bimoleculare superficiale.
Deseori este necesara o comparatie a vitezelor diferitelor reactii.
Aceasta comparatie este transferata uneori constantelor de viteza.
Se pune insa intrebarea: putem compara o constanta de viteza a unei reactii monomoleculare cu o constanta de viteza a unei reactii bimoleculare? Raspunsul este evident NU, deoarece au dimensiuni diferite. Pentru a solutiona problema din punct de vedere dimensional, putem folosi probabilitatea de reactie definita prin ecuatia (21):
![]() (21)
(21)
Comparand cu ecuatiile cinetice ale reactiilor elementare se obtine:
![]() (45)
(45)
pentru reactiile monomoleculare, in care wA k
![]() (46)
(46)
pentru reactiile bimoleculare monocomponente, in care wA kCA
![]() (47)
(47)
pentru reactiile bimoleculare bicomponente, in care wA kCB, iar wB kCA
Se poate verifica usor ca <wj> = s-1, pentru oricare dintre reactii, astfel incat comparatia dintre diferitele probabilitati de reactie nu are nici o restrictie. Pentru reactiile monomoleculare probabilitatile de reactie sunt egale cu constantele de viteza (w k), pentru reactiile bimoleculare monocomponente probabilitatile de reactie sunt egale cu produsul dintre constanta de viteza si concentratia reactantului (w kCA), iar pentru reactiile bimoleculare bicomponente probabilitatile de reactie sunt egale cu produsul dintre constanta de viteza si concentratia celuilalt partener reactant (wA kCB wB kCA
Timpul de viata al unui reactant
Intrucat probabilitatile de reactie wj au semnificatiile unor frecvente de transformare chimica, inversul lor, cu dimensiuni de timp (s), reprezinta timpul de viata (t k ), independent de concentratii pentru reactiile monomoleculare si respectiv timpul momentan de viata pentru reactiile bimoleculare (t kCA sau t kCB ), dependent de concentratia momentana.
Comparatie intre ecuatia cinetica teoretica bazata pe legea actiunii maselor si ecuatia cinetica empirica
Ecuatia cinetica diferentiala a unei reactii elementare poate fi generalizata in forma:
![]() (48)
(48)
unde produsul concentratiilor se refera numai la reactanti, iar coeficientii stoichiometrici se iau in valoare absoluta.
Pe de alta parte, legea empirica este de forma:
![]() (49)
(49)
comparatie a celor doua ecuatii ne conduce la urmatoarele concluzii, cunoscute sub denumirea de regula lui van't Hoff pentru reactii elementare:
Intr-o reactie elementara, ordinele partiale de reactie sunt egale cu valorile absolute ale coeficientilor stoichiometrici (ai reactantilor), iar ordinul global de reactie este egal cu molecularitatea
Ecuatia cinetica diferentiala a unei reactii elementare poate fi stabilita daca se cunoaste ecuatia sa stoichiometrica. Extinderea acestor proprietati ale reactiilor elementare la reactii de complexitate necunoscuta poate sa conduca la concluzii eronate.
Utilizarea notiunii de molecularitate pentru reactii a caror natura este necunoscuta sau pentru reactii complexe este de asemenea improprie. Pentru o reactie complexa se poate vorbi despre molecularitatea fiecarei reactii elementare componente.
Ecuatiile cinetice diferentiale au avantajul simplitatii, dar necesita calculul vitezei de reactie prin derivarea curbei cinetice, operatie care conduce la o amplificare a erorilor experimentale.
Degenerarea ordinului de reactie
Ecuatia cinetica diferentiala
pentru o reactie bimoleculara bicomponenta in forma ![]() arata ca ne
putem astepta la doua comportari extreme:
arata ca ne
putem astepta la doua comportari extreme:
a). cand cele doua concentratii sunt de acelasi ordin de marime, reactia este de ordinul global doi (unu in raport cu fiecare reactant).
b). Cand unul dintre componenti este in exces foarte mare (este component majoritar) in raport cu celalalt (care devine component minoritar), de exemplu CB >> CA, atunci cand componentul minoritar este consumat complet, concentratia componentului
majoritar ramane practic constanta. Ecuatia cinetica
poate fi reorganizata in forma: ![]() , unde k este o pseudo - constanta a
unei reactii de ordin aparent unu.
, unde k este o pseudo - constanta a
unei reactii de ordin aparent unu.
Denumirea de pseudo - constanta reflecta posibilitatea acesteia de schimbare atunci cand excesul se schimba. Desi molecularitatea ramane aceeasi, ordinul global de reactie a degenerat de la doi la unu.
Integrarea ecuatiilor cinetice diferentiale. Ecuatii cinetice integrale
Reactii monomoleculare
Ecuatia diferentiala![]() poate fi
integrata analitic prin separare de variabile:
poate fi
integrata analitic prin separare de variabile: ![]() . Integrarea intre
limitele
. Integrarea intre
limitele ![]() si CA de la t = 0
pana la t conduce la:
si CA de la t = 0
pana la t conduce la: 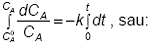
![]() (49)
(49)
Aceasta este ecuatia cinetica integrala, in forma logaritmica, a unei reactii monomoleculare. Ecuatia poate fi adusa si in forma exponentiala:
![]() (50)
(50)
Cele doua forme servesc la evaluarea constantei de viteza si la simularea evolutiei temporale atunci cand se cunoaste constanta de viteza si compozitia initiala.
Evaluarea constantei de viteza se bazeaza pe utilizarea
ecuatiei (49). Graficul ln(CA in functie de timp
conduce la o dreapta cu panta egala cu (-k) si cu intersectia (ordonata la origine)
egala cu ![]()
Ecuatia (50) poate fi folosita pentru simularea unei curbe cinetice, cand se cunosc constanta de viteza si concentratia initiala
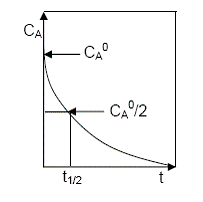
Figura 2. Curba cinetica integrala pentru o reactie monomoleculara
Timpul de injumatatire
Graficul ecuatiei (50) reprezinta o scadere exponentiala a concentratiei CA si poate fi folosit la determinarea timpului de injumatatire a reactantului, dupa cum se ilustreaza in Figura 2.
Daca in ecuatia (49) se considera ![]() se obtine
se obtine![]() . Determinarea
timpului de injumatatire serveste la evaluarea constantei
de viteza. Timpul de injumatatire( t ln 2/k ) este corelat cu timpul
de viata discutat anterior (l k
. Determinarea
timpului de injumatatire serveste la evaluarea constantei
de viteza. Timpul de injumatatire( t ln 2/k ) este corelat cu timpul
de viata discutat anterior (l k
2. Reactii bimoleculare monocomponente
Ecuatia diferentiala ![]() , poate fi
integrata analitic prin separare de variabile:
, poate fi
integrata analitic prin separare de variabile: ![]() . Integrarea intre
limitele
. Integrarea intre
limitele ![]() si CA de la t = 0
pana la t conduce la:
si CA de la t = 0
pana la t conduce la: 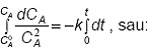
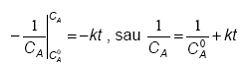 (51)
(51)
Forma finala reprezinta o scadere hiperbolica a concentratiei CA
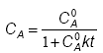 (52)
(52)
Ecuatia integrala serveste atat la evaluarea constantei de viteza, din reprezentarea grafica 1/CA in functie de timp (conform ecuatiei (51)), cat si la simularea unei curbe cinetice, cand se cunosc constanta de viteza si concentratia initiala, utilizand ecuatia (52).
Curba cinetica CA in functie de timp serveste la determinarea
timpului de injumatatire (sau pentru o alta
fractionare), ca si la reactiile monomoleculare. Substituind ![]() in ecuatia (3, 52) se obtine:
in ecuatia (3, 52) se obtine:
![]() (53)
(53)
Spre deosebire de reactiile monomoleculare,
pentru care t este independent de
concentratia initiala, la reactiile bimoleculare
monocomponente t variaza invers
proportional cu ![]()
3. Reactii bimoleculare bicomponente
Ecuatia cinetica diferentiala ![]() in forma ei care contine avansarea
reactiei,
in forma ei care contine avansarea
reactiei, ![]() poate fi integrata prin separare de
variabile:
poate fi integrata prin separare de
variabile:
![]() (54 a)
(54 a)
Descompunerea in fractii simple si integrarea intre limitele ![]() si CA de la t = 0
pana la t conduce la:
si CA de la t = 0
pana la t conduce la:
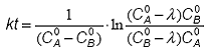 (54
b)
(54
b)
Cand ![]() , ecuatia
cinetica diferentiala (54a) se reduce la forma caracteristica
reactiilor bimoleculare monocomponente, iar cea integrala este de
forma (52).
, ecuatia
cinetica diferentiala (54a) se reduce la forma caracteristica
reactiilor bimoleculare monocomponente, iar cea integrala este de
forma (52).
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1771
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved