| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
PROPRIETATILE SISTEMELOR COLOIDALE
Sistemele coloidale prezinta proprietati cinetico-moleculare, optice, electrice diferite de ale solutiilor.
1. Proprietati cinetico-moleculare
Particulele coloidale suspendate in mediul de dispersie lichid sau gazos prezinta proprietati cinetico-moleculare daca asupra lor actioneaza forta gravitationala, centrifugala sau un gradient de potential chimic rezultat dintr-o diferenta de concentratie a fazei disperse.
Aceste proprietati sunt: sedimentarea, difuzia, miscarea browniana.
1.1. Sedimentarea
Sedimentarea consta in depunerea particulelor coloidale sub actiunea fortei gravitationale sau centrifugale si duce la separarea sistemului coloidal in doua straturi: unul in care concentratia fazei disperse este maxima (sediment) si un strat care contine mediul de dispersie.
Sistemele microeterogene (suspensii, emulsii) sedimenteaza in camp gravitational, in timp ce sistemele ultramicroeterogene (soluri) sedimenteaza in camp centrifugal.
a) Sedimentarea gravitationala
Fiecare particula care sedimenteaza in camp gravitational se misca in interiorul unui mediu de dispersie vascos, fiind supusa la doua forte ce actioneaza in sens opus: forta gravitationala fg si forta de rezistenta vascoasa a mediului fs.
Pentru particula de volum V si densitate ρ1 imersata in mediul de dispersie de densitate ρ2, forta gravitationala este:
fg = m'g = V(ρ1 - ρ2)g (4.2)
unde: g = acceleratia gravitationala;
m' = masa efectiva a particulei, egala cu diferenta dintre masa proprie si cea a mediului de dispersie dezlocuit.
Daca ρ1 > ρ2 are loc depunerea particulelor (suspensii), iar daca ρ1 < ρ2, particulele urca si are loc ecremarea (emulsii). Forta fs este functie de viteza v a particulei conform relatiei:
fs = fv (4.3)
unde: f = coeficientul de frecare.
La inceput fg > fs si miscarea particulei este accelerata deoarece fg este constanta. fs creste odata cu viteza, iar la un moment dat, cele doua forte devin egale, iar particula se deplaseaza uniform cu o viteza constanta numita viteza de sedimentare.
Din egalitatea celor doua forte:
fg = fs (4.4)
respectiv
V(ρ1 - ρ2)g = fv (4.5)
rezulta:
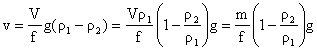 (4.6)
(4.6)
unde: m = masa particulei.
Relatia (4.6) permite evaluarea vitezei de sedimentare independent de forma particulei coloidale daca se cunoaste raportul m/f.
Daca particula este sferica, se foloseste relatia lui Stokes pentru forta de rezistenta vascoasa a mediului de dispersie:
fs = 6 π r η v (4.7)
unde: η = vascozitatea mediului de dispersie;
r = raza particulei sferice.
f = 6 π r η (4.8)
Inlocuind in expresia (4.6) valoarea lui f din ecuatia (4.8) si volumul particulei sferice dat de relatia:
![]() (4.9)
(4.9)
se obtine viteza de sedimentare a particulei coloidale sferice:
![]() (4.10)
(4.10)
unde: C = constanta de sedimentare gravitationala.
Din relatia (4.10) se observa ca viteza de sedimentare creste cu dimensiunea particulei si se aplica sistemelor monodisperse cu particule sferice.
Studiul sedimentarii permite aprecierea dimensiunii particulelor. Metoda de analiza dispersa se numeste sedimentometrie sau analiza de sedimentare.
b) Sedimentarea centrifugala
Pentru analiza dispersa a sistemelor coloidale ultramicroeterogene, macromoleculare si inalt disperse, sedimentarea gravitationala se inlocuieste cu sedimentarea centrifugala.
In camp centrifugal, particula este supusa la actiunea a doua forte de sens contrar: forta centrifuga fc si forta de frecare Stokes, fs. La un moment dat cele doua forte devin egale. Viteza de sedimentare a particulelor sferice este data de relatia:
![]() (4.11)
(4.11)
unde: ω = viteza unghiulara a rotorului centrifugii;
x = distanta particulei fata de axa de rotatie a centrifugii.
Ecuatia (4.11) este asemanatoare cu relatia (4.10), insa in locul acceleratiei gravitationale apare acceleratia centrifugala ω2x.
Intrucat ω2x >> g, viteza de sedimentare creste in acest caz.
In ecuatia (4.11) Svedberg a definit constanta de sedimentare centrifugala S care este egala cu viteza de sedimentare intr-un camp centrifugal de acceleratie unitara, cu expresia:
![]() (4.12)
(4.12)
Svedberg (1923) a construit prima
ultracentrifuga pentru care ω2x ![]() 104
g, ceea ce a permis sa se realizeze sedimentarea unor sisteme inalt disperse (r
= 10-6 cm dintr-un sol de aur). La ultracentrifugile actuale,
valoarea acceleratiei centrifugale a atins 1010 g.
104
g, ceea ce a permis sa se realizeze sedimentarea unor sisteme inalt disperse (r
= 10-6 cm dintr-un sol de aur). La ultracentrifugile actuale,
valoarea acceleratiei centrifugale a atins 1010 g.
1.2. Difuzia
Prin difuzie se intelege procesul spontan de egalizare a concentratiei fazei disperse in volumul intregului sistem coloidal daca forta gravitationala este neglijata.
Sedimentarii i se opune difuzia
particulelor sub actiunea gradientului de concentratie ![]() care apare.
care apare.
Difuzia este descrisa matematic de legile lui Fick (1855).
Se admite ca toate particulele difuzeaza dupa o singura directie, sensul pozitiv al axei x, cu o viteza identica, dintr-un domeniu de concentratie mai mare spre un domeniu de concentratie mai mica.
Forta motoare a difuziei pentru o
particula este gradientul potentialului chimic ![]() :
:
![]() (4.13)
(4.13)
unde: NA = numarul lui Avogadro.
Semnul minus se datoreaza faptului ca atunci cand x creste, potentialul chimic μ scade.
Stiind ca pentru un sistem coloidal diluat, potentialul chimic este dat de relatia μ = μ0 + RTlnc, rezulta:
![]() (4.14)
(4.14)
Inlocuind valoarea dμ data de expresia (4.14) in ecuatia (4.13) se obtine:
![]() (4.15)
(4.15)
unde: ![]() =
constanta lui Boltzmann;
=
constanta lui Boltzmann;
![]() = gradientul de concentratie;
= gradientul de concentratie;
c = concentratia molara a sistemului coloidal.
In conditii de stationaritate, forta de difuzie fd va egala forta de rezistenta vascoasa a mediului de dispersie fs:
![]() (4.16)
(4.16)
Se obtine pentru viteza de difuzie:
![]() (4.17)
(4.17)
Viteza de difuzie se exprima prin numarul de moli ce difuzeaza in unitatea de timp printr-o suprafata S perpendiculara pe directia de deplasare a particulelor coloidale.
Viteza de difuzie este data de legea intai a lui Fick:
![]() (4.18)
(4.18)
unde: D = coeficientul de difuzie.
Coeficientul de difuzie se defineste prin expresia lui Einstein:
![]() (4.19)
(4.19)
Cu cat particula coloidala este mai mare, coeficientul de difuzie are valori mai mici.
1.3. Echilibrul de sedimentare
Prin sedimentare in camp gravitational sau centrifugal, particulele tind sa fie colectate in sediment. Difuzia duce la dispersia lor datorita gradientului de concentratie aparut prin sedimentare.
Cand cele doua procese se compenseaza reciproc, se stabileste un echilibru intre sedimentare si difuzie numit si echilibru de sedimentare.
Se considera ca particulele sedimenteaza in sensul negativ al axei x datorita actiunii campului gravitational, iar pe de alta parte ele sunt solicitate prin difuzie in sensul invers al aceleiasi axe. Echilibrul de sedimentare se concretizeaza prin faptul ca viteza de sedimentare si cea de difuzie devin egale. Tinand cont de relatiile (4.6) si (4.17) rezulta:
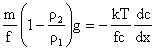 (4.20)
(4.20)
Separand variabilele si definind c1 si c2, concentratiile particulelor in coloana de sistem coloidal la distantele x1 si x2, se obtine prin integrarea ecuatiei (4.20):
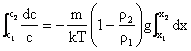 (4.21)
(4.21)
adica
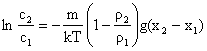 (4.22)
(4.22)
In cazul campului centrifugal, in ecuatia (4.20) acceleratia gravitationala se inlocuieste cu cea centrifugala ω2x, adica:
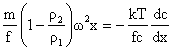 (4.23)
(4.23)
respectiv
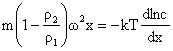 (4.24)
(4.24)
Integrarea ecuatiei (4.24) duce la:
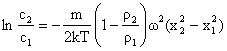 (4.25)
(4.25)
Ecuatiile (4.22) si (4.25) releva faptul ca din masuratori privind echilibrul de sedimentare se pot obtine informatii cu privire la masa m a particulelor, independent de forma lor.
Reprezentarile semilogaritmice ![]() sau
sau ![]() sunt drepte a caror panta este proportionala
cu masa particulelor coloidale, cel putin la sistemele monodisperse. In cazul
polidispersiei apar abateri de la liniaritate.
sunt drepte a caror panta este proportionala
cu masa particulelor coloidale, cel putin la sistemele monodisperse. In cazul
polidispersiei apar abateri de la liniaritate.
Daca se considera x1 = 0
in ecuatia (4.22) drept nivel de zero arbitrar la care concentratia ![]() , se
obtine:
, se
obtine:
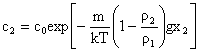 (4.26)
(4.26)
Ecuatia (4.26) se numeste legea hypsometrica sau barometrica a lui Laplace si descrie echilibrul de sedimentare.
Legea hypsometrica se refera la conditii de echilibru, iar echilibrul se stabileste lent in cazul sistemelor cu particule fine.
Viteza de sedimentare este proportionala cu patratul dimensiunii liniare a particulelor conform ecuatiei (4.10), in timp ce viteza de difuzie (conform ecuatiei 4.17) este invers proportionala cu dimensiunea liniara (prin intermediul coeficientului de frecare) astfel incat pe masura ce scade dimensiunea particulei, viteza de sedimentare se micsoreaza mai repede decat creste viteza de difuzie. Rezulta ca echilibrul de sedimentare se va realiza cu atat mai incet cu cat sistemele coloidale sunt constituite din particule mai mici.
In campul gravitational sau centrifugal particulele coloidale se repartizeaza la echilibru astfel incat concentratia lor scade conform legii barometrice. Aceasta scadere este cu atat mai pronuntata cu cat particulele sunt mai grosiere.
Se spune ca sistemele formate din
asemenea particule sunt instabile fata de sedimentare, iar daca particulele
sunt mai fine, sistemele poseda o anumita stabilitate cinetica. Masura acestei
stabilitati pentru un sistem dat este valoarea marimii x1/2 obtinuta
din ecuatia (4.26) cand ![]() .
.
1.4. Miscarea browniana
Miscarea browniana este unul dintre cele mai caracteristice fenomene coloidale. Fenomenul a fost descoperit de botanistul Brown (1828) care a studiat la microscop miscarea dezordonata a unei suspensii apoase de polen. Cauza acestei miscari dezordonate in toate directiile este agitatia termica haotica a moleculelor mediului de dispersie in care se afla suspendate particulele coloidale. Impulsurile moleculare suferite de o particula suficient de mica nu se compenseaza. Drept urmare apare o forta corespunzatoare variatiilor de impuls ce insotesc ciocnirile statistic dezordonate dintre moleculele mediului si particula. Aceasta forta numita si fluctuatie determina miscarea hazardata a particulei.
Aspectul la microscop al miscarii browniene care este o miscare in zig-zag este diferit dupa forma si marimea particulelor.
Teoria miscarii browniene a fost elaborata de Einstein (1905) si independent de Smoluchowski (1906). Ea a fost confirmata de Perrin si Svedberg.
Numarul mediu de impulsuri
moleculare primite de catre o particula este foarte mare, de ordinul 1012/secunda.
Se admite drept marime ce caracterizeaza miscarea browniana, segmentul de
dreapta care uneste punctele in care se afla particula la inceputul si la
sfarsitul unui interval de timp t cunoscut. Proiectia acestui segment pe o axa
orizontala oarecare x se numeste deplasare orizontala a particulei. Este
evident ca trebuie sa se opereze cu o valoare medie, dar simpla medie
aritmetica a deplasarilor orizontale ![]() este nula, conform legii hazardului, datorita
probabilitatilor egale de miscare a particulei in toate directiile. In calcule
se introduce o alta marime numita media patratelor deplasarilor orizontale
este nula, conform legii hazardului, datorita
probabilitatilor egale de miscare a particulei in toate directiile. In calcule
se introduce o alta marime numita media patratelor deplasarilor orizontale ![]() .
.
Miscarea browniana este descrisa de ecuatia lui Einstein:
![]() (4.27)
(4.27)
unde: D = coeficientul de difuzie (cm2/s);
t = timpul;
![]() = media patratelor deplasarilor orizontale ale
particulei.
= media patratelor deplasarilor orizontale ale
particulei.
Einstein a presupus ca miscarea browniana, ca si difuzia este cauzata de agitatia termica, astfel ca miscarea browniana poate fi interpretata din punctul de vedere al difuziei particulelor coloidale. Se poate considera ca difuzia este o consecinta a miscarii browniene.
Tinand cont de relatia (4.19) care pentru particule sferice este:
![]() (4.28)
(4.28)
ecuatia (4.27) devine:
![]() (4.29)
(4.29)
Relatia (4.29) arata ca miscarea browniana este cu atat mai intensa cu cat temperatura este mai mare si vascozitatea mediului de dispersie mai mica. Ea se manifesta intens doar la particulele mici, astfel in mediul de dispersie apos, miscarea browniana apare practic numai la particule cu r ≤ 10-5 cm.
Miscarea browniana a fost cercetata experimental de catre Perrin (1910) care a verificat ecuatia lui Einstein.
Fluctuatiile de impuls care dau nastere miscarii browniene de translatie produc in acelasi timp si o miscare oscilatorie a particulelor coloidale numita miscare browniana de rotatie. Miscarea browniana de rotatie se manifesta in special la particulele asimetrice mai mari care efectueaza numai aceasta miscare.
2. Proprietati optice
Proprietatile optice ale sistemelor coloidale pot fi studiate prin intermediul metodelor care implica interactiunea radiatiei cu materia. Trecerea luminii prin sistemele coloidale se supune legilor reflexiei, refractiei si absorbtiei luminii. O proprietate optica caracteristica coloizilor este efectul Tyndall.
2.1. Absorbtia sistemelor coloidale
Cand un fascicul de lumina traverseaza un strat de sistem coloidal, o parte a luminii este absorbita, ceea ce determina culoarea sistemului, o alta parte este difuzata, iar cea ramasa este lumina transmisa.
Pozitia maximelor curbelor de extinctie se schimba la solutiile coloidale, deplasandu-se spre lungimi de unda din ce in ce mai mari cu cat diametrul particulei respective este mai mare, conform unei reguli stabilite de Ostwald.
In acelasi timp maximul de intensitate al luminii transmise (difuzate) de unii soli atinge cea mai mare valoare pentru o lungime de unda data, caracteristica fiecarui sol si apare efectul de rezonanta optica.
Un sol poate prezenta o culoare in lumina directa si alta culoare in lumina reflectata. Aceasta proprietate se numeste dicroism. Un sol poate avea diverse culori in functie de metodele de preparare a acestuia (ex.: solurile de aur). Aceasta proprietate se numeste policromie. Ea este determinata de forma si marimea particulelor coloidale si de absorbtia selectiva si de difuzia luminii. Astfel, solul de aur, cu particule avand diametrul mai mic de 40 m prezinta culoare rosie, iar cel cu particule avand diametrul mai mare de 60 m are culoare albastra.
2.2. Difractia in sisteme coloidale
Difractia este fenomenul prin care lumina ocoleste obstacolele si are numeroase aplicatii in chimia coloidala.
Fenomenul difractiei s-a aplicat la calculul razei particulelor mici de ceata care produc efectul corona al difractiei luminii soarelui sau a lunii atunci cand particulele sunt de aceeasi marime (monodisperse). Young a construit un aparat de masura a marimii particulelor dispersate, bazat pe efectul corona si numit eriometru.
Solurile examinate in lumina reflectata prezinta fenomenul de opalescenta. Solul se tulbura usor si isi schimba culoarea in domeniul lungimilor de unda mici. Opalescenta este cauzata de difractia luminii si este cu atat mai accentuata cu cat diferenta dintre indicii de refractie ai substantei disperse si ai mediului de dispersie este mai mare.
2.3. Difuzia luminii in sisteme coloidale
Difuzia sau imprastierea luminii de catre sistemele disperse reprezinta cauza a numeroase fenomene naturale cum sunt: culoarea albastra a cerului, curcubeul.
Fenomenul de difuzie a luminii a fost descris pentru prima data de Tyndall (1869), iar Rayleigh (1871) a expus bazele teoretice ale fenomenului. Teoriile asupra difuziei luminii includ si cercetarile lui Mie (1908), Debye (1915) si Gauss (1925).
Cand un fascicul de lumina traverseaza o dispersie coloidala, o parte a luminii incidente este absorbita, iar alta parte este intotdeauna difuzata. Difuzia luminii rezida in faptul ca luminii incidente ii este asociat un camp electric care induce oscilatii periodice ale norilor electronici ai atomilor din mediul material dat, acestia devenind surse secundare ce radiaza lumina difuzata.
Difuzia luminii este pregnanta la sistemele coloidale in care particulele au indicele de refractie diferit de cel al mediului de dispersie. Astfel se explica turbiditatea pronuntata a unor emulsii si suspensii la lumina zilei.
Proiectand un fascicul de lumina printr-o dispersie coloidala si privind perpendicular pe directia incidenta, drumul fasciculului devine vizibil. Pe acest fapt se bazeaza functionarea ultramicroscopului unde fiecare punct luminos aparut in campul intunecat al aparatului indica prezenta unei particule coloidale.
Nefelometria este o alta metoda de studiu a sistemelor coloidale in care se evalueaza lumina difuzata.
Difuzia luminii pentru lungimi de unda din spectrul vizibil poate fi impartita in: difuzie Rayleigh, difuzie Debye si difuzie Mie.
Difuzia Rayleigh este
specifica sistemelor coloidale cu particule sferice, izotrope, avand dimensiuni
mai mici de ![]() din lungimea de unda a luminii folosite.
din lungimea de unda a luminii folosite.
Difuzia Debye este specifica sistemelor disperse, avand particule izotrope, dielectrice, cu dimensiuni comparabile cu lungimea de unda a luminii folosite si cu indicele de refractie apropiat de unitate.
Difuzia Mie este aplicabila tuturor sistemelor coloidale difuzante.
Calcularea intensitatii luminii difuzate se poate realiza pe doua cai: fie considerand difuzia de pe fiecare particula ca urmare a difractiei si interferentei luminii si insumand contributia tuturor particulelor, fie tratand particulele difuzante ca rezultat al fluctuatiilor de densitate sau concentratie ceea ce determina fluctuatii ale constantei dielectrice, respectiv a indicelui de refractie.
Slabirea intensitatii unui fascicul luminos ce strabate un sistem coloidal ca urmare a difuziei poate fi exprimata cantitativ, fie prin intensitatea luminii transmise prin sistem, iar metoda se numeste turbidimetrica, fie se masoara intensitatea luminii difuzate dupa o directie ce face un anumit unghi cu directia initiala de propagare si metoda se numeste difuziometrica.
Daca intensitatea luminii transmise prin sistem este mult mai mica decat cea initiala, se prefera metoda turbidimetrica. Cand intensitatea luminii transmise prin sistemul coloidal este comparabila cu cea initiala, se foloseste metoda de determinare a intensitatii luminii difuzate.
Una din caracteristicile fenomenului de difuzie a luminii consta in polarizarea totala sau partiala a luminii difuzate chiar daca lumina initiala este nepolarizata.
2.3.1. Efectul Tyndall
Daca in fata unei cuve cu pereti plani-paraleli ce contine un sol incolor se aseaza o sursa puternica de lumina alba si un condensator, drumul fasciculului prin cuva devine vizibil. Privind perpendicular pe directia fasciculului incident, se poate observa un con de luminozitate albastruie. Descoperit de Faraday (1857), fenomenul a fost studiat de Tyndall (1869). Acest fenomen nu poate fi pus in evidenta daca in cuva se gaseste o solutie moleculara. Aparitia conului Tyndall se explica prin aceea ca particulele coloidale imprastie in toate partile lumina ce cade asupra lor. Sistemul coloidal este tulbure, opalescent. O astfel de tulbureala este caracteristica multor sisteme coloidale (emulsii, suspensii) chiar la lumina zilei. Modul in care se produce difuzia luminii de catre particule depinde de dimensiunile acestora. Daca raza particulelor este mare fata de lungimea de unda a luminii incidente atunci pe suprafata particulelor se produce reflexia luminii. Daca particulele sunt transparente poate avea loc concomitent refractie si reflexie interna. Razele luminoase deviate de o particula se intalnesc cu alte particule pe care pot suferi din nou reflexii si refractii. Lumina este imprastiata in toate directiile.
Pentru lumina vizibila ( ≈ 10-5 cm), difuzia luminii este caracteristica sistemelor cu o dispersie mai grosiera pentru care r > 10-5 cm. Pentru particule cu r < 10-5 cm, adica pentru un grad de dispersie coloidal, are loc un fenomen de difractie. Daca mediul contine neomogenitati spatiale mici in comparatie cu lungimea de unda a luminii, prin aceste neomogenitati se produce o difractie care se caracterizeaza printr-o redistributie uniforma a luminii in toate directiile. O astfel de difractie prin neomogenitati mici se numeste difuzia luminii.
In sistemele microeterogene si ultramicroeterogene, neomogenitatile spatiale sunt particulele coloidale. Din acest motiv, sistemele coloidale sunt medii optic neomogene sau tulburi si vor prezenta puternic fenomenul de difuzie a luminii.
2.3.2. Legea lui Rayleigh
La trecerea luminii printr-un mediu material, ea provoaca electronilor din acest mediu oscilatii fortate. Rezultatul acestor oscilatii este aparitia unor unde secundare. Ca urmare, o parte a energiei aduse de unda incidenta este imprastiata in toate directiile sub forma undelor secundare si apare difuzia luminii. Undele secundare care merg in alte directii decat cea primara pot sa se compenseze mutual intr-o masura apreciabila astfel ca difuzia sa fie slaba. Simpla prezenta a electronilor nu poate explica difuzia. Pentru ca ea sa se produca, este necesar perturbarea omogenitatii mediului. In acest caz, mici portiuni ale mediului, apropiate intre ele si egale ca volum, devin sursa unor unde secundare de intensitati diferite. Aceste unde nu se mai pot compensa mutual si apare o redistribuire a energiei luminoase pe diferite directii, adica difuzia luminii.
Pentru ca un electron in oscilatia sa fortata sa dea nastere unei unde electromagnetice secundare, el trebuie sa se miste accelerat, iar miscarea sa sub actiunea undei luminoase se supune legii armonice:
x = asin ωt = asin 2πνt (4.30)
unde: a = amplitudinea oscilatiei;
ν = frecventa;
t = timpul.
Acceleratia sa va fi derivata de ordinul doi:
![]() (4.31)
(4.31)
Intensitatea Id a undei secundare emise (luminii difuzate) este proportionala cu amplitudinea, respectiv patratul acceleratiei:
![]() (4.32)
(4.32)
Se stie ca:
![]() (4.33)
(4.33)
unde: c = viteza luminii;
= lungimea de unda a luminii.
Relatia (4.32) devine:
![]() (4.34)
(4.34)
Ecuatia (4.34) este cunoscuta sub numele de legea lui Rayleigh (1871). Proportionalitatea inversa cu puterea a patra a lungimii de unda explica faptul ca lumina difuzata este bogata in radiatii cu lungime de unda mica, adica albastre, daca lumina incidenta este alba (cazul conului Tyndall). Cand lumina incidenta este monocromatica, radiatia difuzata are aceeasi lungime de unda cu cea incidenta.
Legea lui Rayleigh este aplicabila sistemelor ultramicroeterogene ale caror particule au dimensiunile mai mici decat 1/20 din lungimea de unda a luminii (r = 410-6 - 510-6 cm). In cazul particulelor mai mari, cu r > 510-6 cm, relatia dintre intensitatea luminii difuzate si lungimea de unda se schimba, adica exponentul lui λ se micsoreaza. Ecuatia (4.34) devine:
![]() (4.35)
(4.35)
Pentru particule foarte mari se ajunge la:
![]() (4.36)
(4.36)
In acest caz, faptul ca intensitatea luminii difuzate nu mai depinde de lungimea de unda se explica prin aceea ca imprastierea luminii nu se datoreaza difuziei, ci reflexiilor si refractiilor succesive pe suprafata particulelor. Astfel, ceata compusa din particule fine are o nuanta albastra (difuzie Rayleigh), iar la cea cu particule mai mari apare alba.
Generalizand legea lui Rayleigh pentru particule de orice marime, ecuatia (4.34) devine:
![]() (4.37)
(4.37)
unde: 4 ≥ z ≥ 0.
Ecuatia (4.37) reprezinta ecuatia lui Teorell. Prin logaritmarea ecuatiei (4.37) se obtine:
![]() (4.38)
(4.38)
ceea ce reprezinta ecuatia unei drepte. Reprezentand grafic lgId = f(lg ) se obtine o dreapta din a carei panta se obtine z. Cunoscand z, se poate determina raza particulelor. Variatia exponentului z al lungimii de unda a luminii difuzate in functie de raza particulelor coloidale este prezentata in fig. 4.1. Curba este trasata dupa datele lui Teorell (1930) pentru particule de mastic.
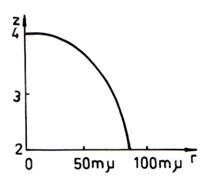
Fig. 4.1. Dependenta dintre exponentul lungimii de unda
a luminii difuzate si dimensiunea particulelor
coloidale
Intensitatea, polarizarea si distributia unghiulara a luminii difuzate de catre un sistem coloidal depind de dimensiunile, forma si concentratia particulelor difuzante. Daca dimensiunea particulelor este mica in comparatie cu lungimea de unda a luminii si ele nu absorb lumina (sunt incolore), intensitatea luminii difuzate Id este data de Rayleigh:
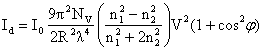 (4.39)
(4.39)
unde: ![]() =
intensitatea luminii incidente;
=
intensitatea luminii incidente;
R = distanta la care se face observarea;
V = volumul fiecarei particule;
= lungimea de unda a luminii difuzate;
NV = numarul de particule din unitatea de volum;
![]() = unghiul dintre directia de observare si cea
incidenta;
= unghiul dintre directia de observare si cea
incidenta;
n1 = indicele de refractie al fazei disperse;
n2 = indicele de refractie al mediului de dispersie.
Ecuatia (4.39) sta la baza metodei ultramicroscopice si nefelometrice de cercetare a sistemelor coloidale.
3. Proprietati electrice
La suprafetele de separare dintre faze apar sarcini electrice care dau nastere la o diferenta de potential electric intre cele doua faze ca urmare a unei distributii neuniforme a sarcinilor. Datorita acestor interactiuni specifice, sarcinile de un anumit semn se acumuleaza la interfata, iar cele de semn contrar vor fi atrase de primele prin interactiuni electrostatice si se formeaza stratul dublu electric.
Incarcarea electrica a sistemelor coloidale se evidentiaza prin fenomenele electrocinetice generate ca: electroforeza, electroosmoza.
3.1. Originea sarcinilor electrice in sistemele coloidale
In sistemele coloidale, sarcinile electrice sunt determinate de ionii care pot proveni din faza dispersa sau din solutia cu care aceasta vine in contact. Semnul sarcinii particulelor coloidale depinde de adsorbtia relativa de anioni si cationi sau de natura ionilor formati prin disocierea fazei disperse. Daca suprafata fazei disperse adsoarbe mai multi anioni, ea se va incarca negativ.
Pentru cazul interfetei dintre doua substante pure, regula lui Cohen postuleaza ca cea cu constanta dielectrica mai mare se incarca pozitiv. Ex.: incarcarea negativa a coloizilor in apa care are constanta dielectrica mare .
Aparitia sarcinilor electrice in sistemele coloidale poate fi determinata de urmatoarele fenomene:
a) disocierea grupelor ionogene continute in substanta care formeaza faza dispersa.
Aceasta situatie este specifica coloizilor de asociatie ionici. Grupe de tipul -COOH, -NH2, -SO3Me sunt intalnite in acesti compusi. Cand aceeasi molecula contine atat grupe acide cat si bazice, sistemul se numeste amfoter si sarcina rezultata prin disociere depinde de pH-ul mediului, existand un pH numit izoelectric pentru care incarcarea este nula.
b) adsorbtia ionilor din solutie este principala cale de formare a stratului dublu electric pe dispersiile liofobe.
In cazul formarii sistemelor coloidale prin reactii de condensare, cand unul din reactanti este in exces, se vor adsorbi acei ioni care intra si in compozitia coloidului. De exemplu, la formarea solului de AgI in exces de AgNO3, acesta va deveni pozitiv ca urmare a adsorbtiei ionilor Ag+. Daca excesul este de KI, solul devine negativ datorita adsorbtiei ionilor I-.
Sistemele coloidale poseda o conductivitate electrica redusa care este determinata de incarcarea electrica a suprafetelor de separare. Datorita sarcinilor electrice ale sistemelor coloidale, se produce migratia particulelor coloidale sub actiunea curentului electric.
3.2. Stratul dublu electric
Existenta unui potential caracteristic sistemelor coloidale se explica la fel ca si potentialul de electrod pe baza stratului dublu electric. Cea dintai abordare a stratului dublu electric care apare la interfata particulelor coloidale apartine lui Helmholtz (1853). Acesta presupune ca ionii adsorbiti la interfata atrag ionii de semn contrar (contraionii) din solutie. Apare stratul dublu electric, cele doua straturi de sarcini electrice asemanandu-se cu armaturile unui condensator intre care apare un salt al potentialului electric. Modelul Helmholtz este ilustrat in fig. 4.2.
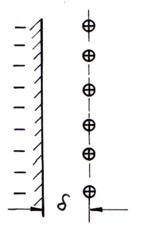
Fig. 4.2. Modelul Helmholtz al stratului dublu electric
Modelul lui Gouy (1910) si Chapmann (1913) numit si modelul stratului dublu difuz, considera ca distributia contraionilor pe distante mari fata de interfata este o urmare a agitatiei termice, formand un nor ionic in solutie.
Interfata incarcata va fi inconjurata de un nor ionic difuz in care se gasesc cu precadere ioni de semn contrar (contraioni) si in mod intamplator ioni de aceeasi sarcina cu interfata. Modelul Gouy-Chapmann al stratului dublu electric este prezentat in fig. 4.3.
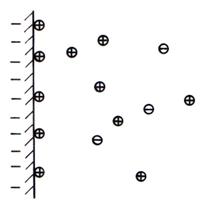
Fig. 4.3. Modelul Gouy-Chapmann al stratului dublu electric
Modelul Stern (1924) considera dimensiunea finita a ionilor care limiteaza distanta minima pana la care se pot apropia de interfata. Modelul Stern este o sinteza a celor doua modele anterioare, considerand stratul dublu electric format dintr-un strat fix (compact) si un strat difuz al ionilor. O parte din contraioni se afla in stratul fix la o anumita distanta de interfata incarcata electric, iar restul de contraioni se dispun sub forma stratului difuz. Modelul Stern se numeste si modelul stratului dublu mixt si este ilustrat in fig.
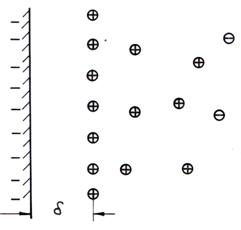
Fig. Modelul Stern al stratului dublu electric
Modelul Grahame (1947) distinge in interiorul stratului compact de tip Stern, doua planuri paralele cu interfata (suprafata solida): planul Helmholtz extern (PHE) situat in planul care contine contraionii hidratati la distanta δ de interfata incarcata si planul Helmholtz intern (PHI) in care se afla ionii adsorbiti specific, deshidratati. Ionii aflati in contact direct cu interfata solida nehidratata se numesc ioni de contact sau adsorbiti specific. Modelul Grahame al stratului dublu electric este prezentat in fig. 4.5.
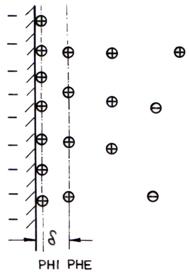
Fig. 4.5. Modelul Grahame al stratului dublu electric
In toate modelele mentionate nu s-a luat in considerare prezenta moleculelor de solvent aflate in contact cu interfata. Moleculele de solvent intra in competitie cu ionii adsorbiti specific la interfata, conform modelului elaborat de Bockris si Reddy (1970).
3.3. Potentialul electrocinetic
Structura stratului dublu electric permite intelegerea fenomenelor ce apar la miscarea reciproca a doua faze in contact. Existenta potentialului electrocinetic este legata de stratul dublu electric. Stratul Stern de grosime este rigid legat de suprafata solida a particulei coloidale, fiind practic imobil, in timp ce stratul difuz Gouy (d) prezinta o mobilitate pronuntata.
Limita de separatie dintre cele doua parti ale stratului dublu electric se numeste plan de alunecare. El este situat in partea difuza a stratului dublu electric si se poate deplasa spre suprafata (interfata) solida cel mult pana la planul Helmholtz extern.
Potentialul in planul de alunecare determinat de densitatea de sarcina in acest plan se numeste potential electrocinetic. Particulele coloidale se afla in miscare browniana. Partea difuza mobila a stratului dublu electric se gaseste in mediul de dispersie, ea fiind deplasata fata de cea compacta, aderenta la suprafata particulelor coloidale. Apare un excedent de sarcini pe suprafata solida a particulelor coloidale, acestea incarcandu-se fata de faza lichida la un potential electric care este potentialul electrocinetic definit de relatia:
![]() (4.40)
(4.40)
unde: ζ = potentialul electrocinetic;
= densitatea de sarcina din stratul difuz;
d = grosimea stratului difuz;
= constanta dielectrica a mediului.
3.4. Fenomene electrocinetice
In orice sistem coloidal cand una din faze se misca fata de cealalta, potentialul electrocinetic determina fenomene electrocinetice. Sunt posibile doua situatii:
a) O diferenta de potential exterioara provoaca miscarea reciproca a fazelor si determina fenomenele de electroforeza (soluri, suspensii) si electroosmoza (sisteme capilare).
b) O forta mecanica exterioara (presiune, forta gravitationala) provoaca miscarea unei faze fata de cealalta si determina aparitia unei diferente de potential electric ceea ce se concretizeaza in potential de curgere la deplasarea mediului de dispersie si potential de sedimentare la deplasarea fazei disperse.
3.4.1. Electroforeza
Daca particulele unui sistem coloidal se afla intr-un camp electric, sub actiunea acestuia, ionii din stratul mobil difuz se deplaseaza spre polul de sarcina contrara. Mediul de dispersie lichid este imobil.
Deplasarea unilaterala a particulelor coloidale (fazei disperse) incarcate spre unul din electrozii conectati la o sursa de curent continuu se numeste electroforeza.
Acest fenomen electrocinetic a fost descoperit de Reiss.
Viteza de deplasare a particulelor coloidale in camp electric este data de relatia:
![]() (4.41)
(4.41)
unde: ζ = potentialul electrocinetic;
E = intensitatea campului electric;
= coeficientul de vascozitate a mediului de dispersie;
= constanta dielectrica a mediului.
Daca E = 1 se defineste mobilitatea electroforetica a particulelor coloidale:
![]() (4.42)
(4.42)
Cunoscand mobilitatea electroforetica, se poate determina potentialul electrocinetic al particulelor coloidale in volti, folosind relatia (4.42):
![]() (4.43)
(4.43)
Determinarea experimentala a mobilitatii electroforetice a particulelor coloidale se poate realiza prin diferite metode:
metode macroscopice care urmaresc viteza de deplasare a limitei de separatie dintre sistemul coloidal cercetat (sol, suspensie) si un lichid auxiliar in care sunt introdusi electrozii conectati la sursa de curent continuu;
metode microscopice care urmaresc deplasarea individuala a particulelor in camp electric cu ajutorul microscopului sau ultramicroscopului;
metode speciale la care migrarea particulelor coloidale are loc in capilarele unui material poros (hartie de filtru, acetat de celuloza, poliacrilamida): electroforeza zonala.
Electroforeza prezinta aplicatii multiple. In industria portelanului se utilizeaza la purificarea caolinei. De asemenea se foloseste la acoperiri cu latex de cauciuc a suprafetelor metalice si a tesaturilor textile. Eletroforeza zonala (pe hartie) are aplicatii in biologie si in biochimia clinica, la studiul proteinelor.
3.4.2. Electroosmoza
Electroosmoza consta in deplasarea mediului de dispersie prin peretii membranelor semipermeabile sau capilare sub actiunea unui camp electric.
Fenomenul electrocinetic a fost pus in evidenta de catre Reiss in 1807.
Explicatia fenomenului electrocinetic rezulta din structura stratului dublu electric de la suprafata capilarelor cum sunt membranele, diafragmele, materialele poroase. Daca suprafata este incarcata negativ, in stratul difuz mobil se afla ionii pozitivi. Sub influenta campului electric, stratul difuz se deplaseaza spre catod, antrenand in aceasta miscare mediul de dispersie. Datorita existentei stratului difuz, mediul de dispersie are sarcina electrica si ca urmare el se deplaseaza spre unul din electrozi.
Incarcarea electrica a suprafetei capilarelor care determina fenomenul de electroosmoza se datoreaza fie unei ionizari superficiale, fie adsorbtiei de ioni. Astfel, sticla se incarca negativ deoarece ionii alcalini trec usor in solutie, in timp ce macroanionii (silicat), voluminosi, raman la suprafata. In acest mod se explica ca toate materialele poroase cu caracter acid se incarca negativ deoarece trimit ionii H+ in solutie (ex.: cuart, portelan, lemn, hartie de pergament). Materialele cu caracter bazic (ex.: corindon, carbonat de calciu) se vor incarca superficial pozitiv, trimitand anionii in solutie. Daca suprafata solida nu se ionizeaza (ex.: carbune), aproape intotdeauna se incarca negativ in contact cu apa datorita adsorbtiei ionilor OH-.
Electroosmoza se caracterizeaza prin viteza de migrare a moleculelor mediului de dispersie (relatia 4.41), identica cu viteza de deplasare a particulelor coloidale la electroforeza si prin debitul sau volumul de lichid scurs in unitatea de timp prin diafragma formata din capilare, conform relatiei:
![]() (4.44)
(4.44)
unde: V = volumul de lichid scurs in unitatea de timp prin diafragma;
I = intensitatea curentului electric;
η = coeficientul de vascozitate a mediului de dispersie;
= conductivitatea mediului de dispersie (lichidului);
ζ = potentialul electrocinetic;
ε = constanta dielectrica a mediului.
Cunoscand volumul de lichid scurs in unitatea de timp prin diafragma, se poate determina potentialul electrocinetic, in volti, folosind relatia (4.41):
![]() (4.45)
(4.45)
Electroosmoza are numeroase aplicatii tehnice. Prin electroosmoza se separa apa din unele sisteme capilare cum sunt: turba, argila, caolinul cat si din unele produse alimentare (gelatina).
Materialele poroase pot fi impregnate cu solutiile unor substante care le maresc valoarea. De exemplu, lemnul se impregneaza cu substante conservante, iar pieile supuse tabacirii se trateaza electroosmotic cu solutii de tananti.
O aplicatie biomedicala a electroosmozei este analiza curgerii in tuburile renale.
3.4.3. Potentialul de curgere
Se presupune ca in cazul electroosmozei se inverseaza conditiile de lucru. In loc ca mediul de dispersie (lichidul) sa migreze sub actiunea unui camp electric exterior, se va exercita o presiune exterioara care forteaza lichidul sa curga prin capilare. Se constata ca intre cei doi electrozi apare o diferenta de potential Ec numita potential de curgere.
Aparitia potentialului de curgere prin capilare este fenomenul invers electroosmozei si se datoreaza potentialului electrocinetic de la suprafata capilarelor.
Fenomenul electrocinetic a fost semnalat de catre Quinque in 1859.
3. Potentialul de sedimentare
In 1880 Dorn a constatat ca daca in drumul particulelor coloidale care sedimenteaza in camp gravitational sau centrifugal, se aseaza doi electrozi, intre acestia apare gradientul de potential Es numit potential de sedimentare.
Potentialul de sedimentare este determinat de incarcarea electrica a particulelor, respectiv de potentialul electrocinetic. Fenomenul este reciproc electroforezei. In loc ca particulele sa migreze sub actiunea unei diferente exterioare de potential, miscarea lor in absenta sursei de curent da nastere unui potential electric.
Acest fenomen electrocinetic se produce accentuat la sedimentarea aerosolilor.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 5331
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved