| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
APROXIMAREA FUNCTIILOR
1. INTRODUCERE
Prin
aproximarea unei functii ![]() , se intelege inlocuirea acesteia cu o
alta functie convenabila
, se intelege inlocuirea acesteia cu o
alta functie convenabila ![]() . Aceasta operatie se
realizeaza atunci cand functia
. Aceasta operatie se
realizeaza atunci cand functia ![]() este
greu de calculat (prin derivare sau integrare), iar functia
este
greu de calculat (prin derivare sau integrare), iar functia ![]() are o
expresie mai simpla, convenabila calculului numeric. Aproximarea
functiilor se face si atunci cand functia
are o
expresie mai simpla, convenabila calculului numeric. Aproximarea
functiilor se face si atunci cand functia ![]() este
obtinuta grafic sau din experimentari si se cere imaginea
analitica a acesteia.
este
obtinuta grafic sau din experimentari si se cere imaginea
analitica a acesteia.
La baza aproximarii functiilor stau mai multe principii, si anume:
- principiul interpolarii;
- principiul celor mai mici patrate (minipatrat Gauss);
- principiul maximelor minime (minimax Cebisev).
Fie ![]() , cu
, cu ![]() , pentru care se cunosc valorile
, pentru care se cunosc valorile 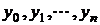 in
nodurile
in
nodurile ![]() . Se cere determinarea unei functii
analitice
. Se cere determinarea unei functii
analitice ![]() , destul de simpla, care sa
aproximeze functia
, destul de simpla, care sa
aproximeze functia ![]() . Functia
. Functia ![]() fiind
imaginea analitica a functiei
fiind
imaginea analitica a functiei ![]() , operatia de aproximare poarta
numele de interpolare si nu are
solutie unica deoarece prin (n+1)
puncte:
, operatia de aproximare poarta
numele de interpolare si nu are
solutie unica deoarece prin (n+1)
puncte: ![]() , se pot trasa o infinitate de curbe.
, se pot trasa o infinitate de curbe.
De
regula, pentru functia ![]() se
foloseste o combinatie liniara de functii simple,
adica un polinom de functii de forma:
se
foloseste o combinatie liniara de functii simple,
adica un polinom de functii de forma:
![]() (2.1)
(2.1)
Acest polinom de functii se particularizeaza in:
polinom de puteri:
![]() (2.2)
(2.2)
polinom trigonometric:
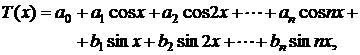 (2.3)
(2.3)
polinom de exponentiale reale:
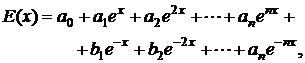 (2.4)
(2.4)
polinom de exponentiale complexe:
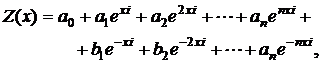 (2.5)
(2.5)
polinom de functii speciale: Legendre, Laguere, Hermite, Cebisev.
Pentru
o retea de noduri ![]() considerate distincte, presupunem cunoscute
valorile
considerate distincte, presupunem cunoscute
valorile 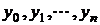 . Avand in vedere ca functia este
data tabelar, nu putem determina valoarea functiei intr-un punct al
carui abscisa difera de nodurile considerate, decat daca
apelam la o formula de interpolare. Se va incepe studiul
aproximarii functiilor prin interpolare cu cea mai simpla
metoda, si anume: interpolarea liniara.
. Avand in vedere ca functia este
data tabelar, nu putem determina valoarea functiei intr-un punct al
carui abscisa difera de nodurile considerate, decat daca
apelam la o formula de interpolare. Se va incepe studiul
aproximarii functiilor prin interpolare cu cea mai simpla
metoda, si anume: interpolarea liniara.
Din
setul de puncte date, consideram doar doua puncte, si anume: ![]() si
si ![]() (fig. 2.1).
(fig. 2.1).
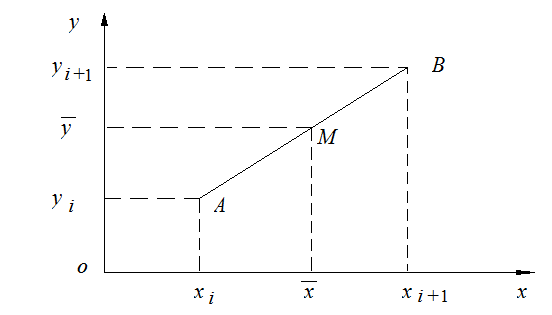
Fig. 2.1. Imaginea interpolarii liniare
Pentru a determina valoarea ![]() , intr-un punct
, intr-un punct ![]() (
(![]() ), vom considera ecuatia dreptei ce trece
prin cele doua puncte A si B, si anume:
), vom considera ecuatia dreptei ce trece
prin cele doua puncte A si B, si anume:
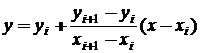 (2.9)
(2.9)
Pentru
![]() , rezulta:
, rezulta:
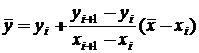
Se
demonstreaza [11] ca eroarea de trunchiere in nodul considerat ![]() , folosind interpolarea liniara, este:
, folosind interpolarea liniara, este:
![]() (2.10)
(2.10)
Deoarece, in general,
functiile de interpolat difera de o functie liniara, se
procedeaza la interpolarea polinomiala, cu gradul polinomului mai
mare sau egal cu doi. In cazul interpolarii patratice, se considera
trei puncte consecutive ![]()
![]() si
si
![]() (fig. 2.2) si se presupune ca prin
cele trei puncte trebuie sa treaca graficul unei functii de
forma:
(fig. 2.2) si se presupune ca prin
cele trei puncte trebuie sa treaca graficul unei functii de
forma:
![]() . (2.11)
. (2.11)
unde ![]() .
.
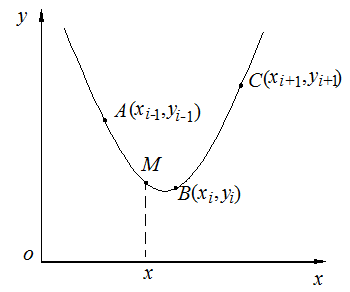
Fig. 2.2. Imaginea interpolarii patratice
Pentru determinarea
coeficientilor ![]() si
si
![]() , se inlocuieste x, din relatia
(2.11), succesiv cu
, se inlocuieste x, din relatia
(2.11), succesiv cu ![]()
![]()
![]() si se obtin
ecuatiile:
si se obtin
ecuatiile:
![]() (2.12)
(2.12)
![]() (2.13)
(2.13)
![]() (2.14)
(2.14)
Relatiile
(2.12), (2.13) si (2.14) formeaza un sistem de trei ecuatii
liniare in necunoscutele ![]() si
si
![]() , sistem ce se poate rezolva analitic sau
numeric (de exemplu, prin metoda eliminarii gaussiene).
, sistem ce se poate rezolva analitic sau
numeric (de exemplu, prin metoda eliminarii gaussiene).
Fie o functie ![]() , pentru care se cunosc valorile
, pentru care se cunosc valorile ![]() in nodurile
in nodurile ![]() presupuse
echidistante, adica:
presupuse
echidistante, adica: ![]()
![]() , h fiind pasul
retelei. Se pune problema determinarii unui polinom de grad mai mic
sau egal cu n, care sa
satisfaca conditiile de interpolare:
, h fiind pasul
retelei. Se pune problema determinarii unui polinom de grad mai mic
sau egal cu n, care sa
satisfaca conditiile de interpolare:
![]()
![]() (2.15)
(2.15)
Pentru aproximarea functiei f, se va considera un polinom de forma:
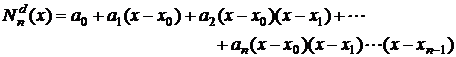 (2.16)
(2.16)
Folosind conditiile de interpolare (2.15) si expresia (2.16), se obtine:
- pentru ![]()
![]()
- pentru ![]()
![]()
- pentru ![]()
![]()
.........................
- pentru ![]()
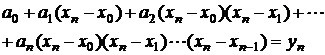
Nodurile fiind echidistante, se pot scrie relatiile:
![]() (2.17)
(2.17)
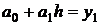 (2.18)
(2.18)
![]() (2.19)
(2.19)
.................
![]() (2.20)
(2.20)
Din relatia (2.17) se
obtine coeficientul ![]() , si anume:
, si anume:
![]()
Inlocuind valoarea lui ![]() in relatia (2.18),
se obtine:
in relatia (2.18),
se obtine:
![]() (2.21)
(2.21)
In mod analog se obtin si ceilalti coeficienti, si anume:
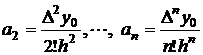 (2.22)
(2.22)
Prin inlocuirea valorilor coeficientilor din expresiile (2.17), (2.21) si (2.22), in relatia (2.16), se obtine:
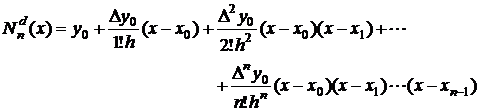 (2.23)
(2.23)
Pentru intocmirea programului
de calcul se face o schimbare de notatie, si anume ![]() . In acest caz, polinomul (2.23) devine:
. In acest caz, polinomul (2.23) devine:
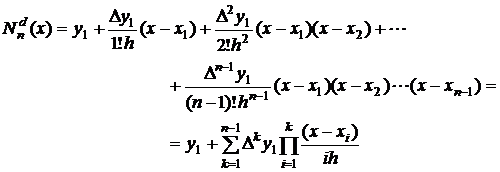 (2.23')
(2.23')
2.4.2. Polinom de interpolare Newton stanga
(cu diferente finite regresive)
Polinomul Newton de interpolare stanga are forma:
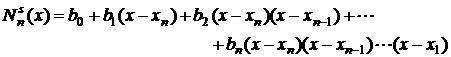 (2.25)
(2.25)
Pentru determinarea
coeficientilor ![]() se folosesc
conditiile de interpolare:
se folosesc
conditiile de interpolare:
![]()
![]() . (2.26)
. (2.26)
Astfel:
- pentru ![]()
![]()
- pentru ![]()
![]()
- pentru ![]()
![]() .........................
.........................
- pentru ![]()
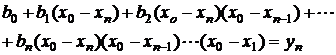 (2.27)
(2.27)
Nodurile fiind echidistante, din relatiile (2.27) se obtin
coeficientii ![]()
![]()
![]() , de forma:
, de forma:
![]()
![]() (2.28)
(2.28)
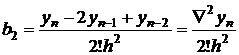
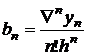
Dupa inlocuiri in relatia (2.25), se obtine:
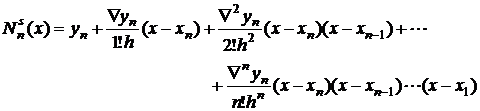 (2.29)
(2.29)
Fie ![]() , pentru care se cunosc valorile
, pentru care se cunosc valorile ![]() in punctele
in punctele ![]() din intervalul
din intervalul ![]() . Punctele sunt considerate echidistante, iar pasul
retelei este h. Pentru
aproximarea functiei f, se construieste un polinom de interpolare
pornind de la un punct
. Punctele sunt considerate echidistante, iar pasul
retelei este h. Pentru
aproximarea functiei f, se construieste un polinom de interpolare
pornind de la un punct ![]() interior intervalului
interior intervalului ![]() , care conduce la o eroare minima de interpolare pentru
, care conduce la o eroare minima de interpolare pentru ![]()
Polinomul Gauss de interpolare de prima speta este de forma:
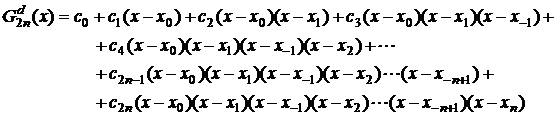 (2.31) sau
(2.31) sau
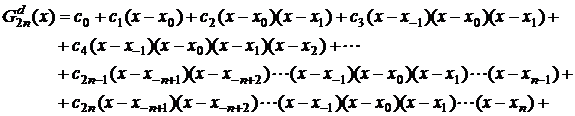 (2.32)
(2.32)
Pentru determinarea constantelor ![]() se pun conditiile
de interpolare:
se pun conditiile
de interpolare:
![]()
![]()
Astfel:
- pentru ![]()
![]()
- pentru ![]()
![]()
- pentru ![]()
![]()
- pentru ![]()
![]()
Folosind relatiile
anterioare, se obtin coeficientii ![]() , dupa cum urmeaza:
, dupa cum urmeaza:
![]()
![]() (2.33)
(2.33)
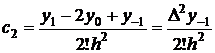
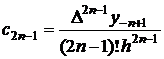
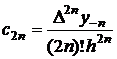
Dupa inlocuiri in relatia (2.32), se obtine:
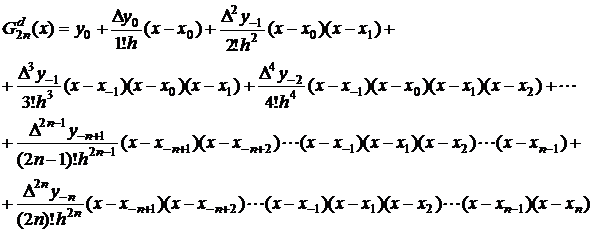
(2.34)
Daca se face schimbarea
de variabila ![]() , rezulta:
, rezulta:
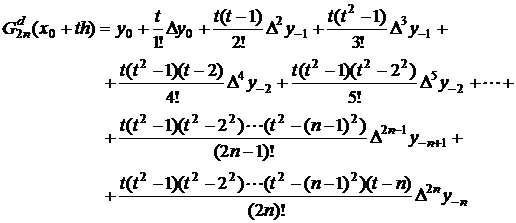 (2.35)
(2.35)
Polinomul Gauss de interpolare de speta a doua este de forma:
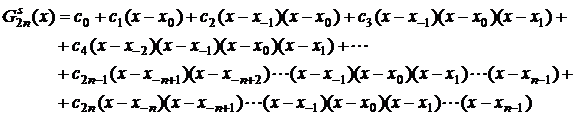
(2.36)
Pentru determinarea constantelor ![]() , se pun conditiile de interpolare:
, se pun conditiile de interpolare:
![]()
![]()
Astfel:
- pentru ![]()
![]()
- pentru ![]()
![]()
- pentru ![]()
![]()
- pentru ![]()
![]()
Folosind relatiile anterioare, se obtine:
![]()
![]()
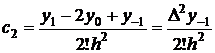
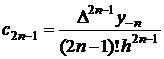
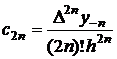
Dupa inlocuiri in relatia (2.36), se obtine:
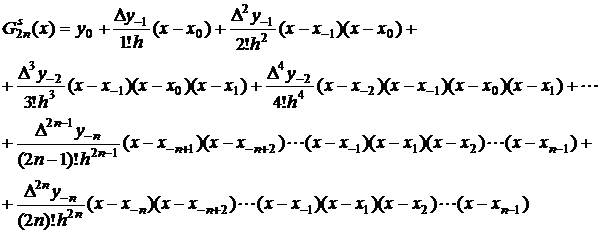
(2.37)
Daca se face schimbarea
de variabila ![]() , rezulta:
, rezulta:
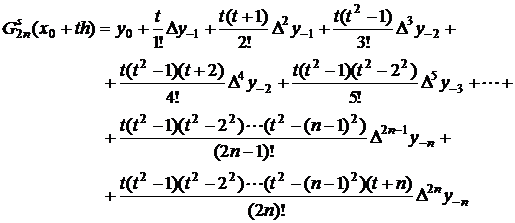 (2.38)
(2.38)
Fie ![]() , si
, si ![]() (n+1) puncte din intervalul
(n+1) puncte din intervalul ![]() , pentru care se cunosc valorile
, pentru care se cunosc valorile ![]() . Punctele sunt considerate echidistante, iar pasul
retelei este h. Pentru
aproximarea functiei f, se
construieste un polinom de interpolare de forma:
. Punctele sunt considerate echidistante, iar pasul
retelei este h. Pentru
aproximarea functiei f, se
construieste un polinom de interpolare de forma:
![]() (2.39)
(2.39)
unde ![]() reprezinta
polinoame de gradul n.
Conditiile de interpolare sunt:
reprezinta
polinoame de gradul n.
Conditiile de interpolare sunt:
![]()
![]() (2.40)
(2.40)
Pentru a obtine forma polinoamelor ![]() , se pun conditiile de interpolare (2.40), si
anume:
, se pun conditiile de interpolare (2.40), si
anume:
![]()
![]()
.........
![]()
Prin identificare, rezulta:
![]()
![]()
![]()
![]()
![]()
![]() (2.41)
(2.41)
...........
![]()
![]()
![]()
Din relatiile (2.41), rezulta ca fiecare
dintre polinoamele ![]() are n zerouri distincte, ceea ce
inseamna ca un polinom oarecare,
are n zerouri distincte, ceea ce
inseamna ca un polinom oarecare, ![]() , are forma:
, are forma:
![]() (2.42)
(2.42)
Constantele ![]() se determina din
conditiile:
se determina din
conditiile: ![]()
![]() , si sunt de forma:
, si sunt de forma:
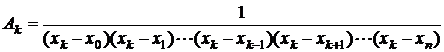 (2.43)
(2.43)
Daca se inlocuiesc relatiile (2.42) si (2.43) in relatia (2.39), se obtine polinomul Lagrange de interpolare, de forma:
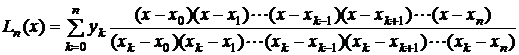 (2.44)
(2.44)
Forma polinomului Lagrange se simplifica daca se face notatia:
![]() (2.45)
(2.45)
Derivata functiei ![]() este:
este:
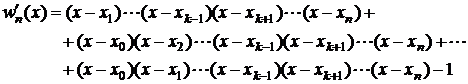 (2.46)
(2.46)
Daca se inlocuieste ![]() cu
cu ![]() , se obtine:
, se obtine:
![]() (2.47)
(2.47)
astfel ca polinomul de interpolare Lagrange devine:
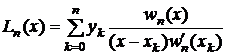 (2.48)
(2.48)
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3404
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved