| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Fie
si 
de dimensiune n+1. Dorim sa gasim o aproximanta 
astfel incat 
.
Scriem
(1)
unde 
este o baza a lui 
Coeficientii sunt solutiile ecuatiilor normale
(2)
Daca
sistemul este ortogonal,
coeficientii se pot obtine cu ajutorul formulelor
(3)
Aproximanta poate fi continua sau discreta, in functie de masura aleasa in definitia produsului scalar. In cazul continuu produsul scalar are forma
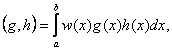
iar in cazul discret
Sa consideram relatia de recurenta pentru polinoamele ortogonale monice
|
|
unde
|
|
Coeficientii din relatia de recurenta (4) au expresia
|
|
Reamintim cateva dintre polinoamele ortogonale si coeficientii din relatiile lor de recurenta:
|
w(t) |
[a,b] |
Pol. ort. |
k |
k |
|
Legendre |
2(k=0) (4-k-2)-1 (k>0) |
|||
|
|
Cebisev I |
(k=0) 1/2 (k=1) 1/4 (k>1) |
||
|
|
Cebisev II |
/2 (k=0) 1/4 (k>0) |
||
|
|
¥ |
Laguerre |
2k+ |
) (k=0) k(k+ ) (k>0) |
|
|
¥ ¥ |
Hermite |
(k=0) k/2 (k>0) |
Probleme propuse.
Sa se gaseasca aproximanta
discreta prin metoda celor mai mici patrate pentru ponderea w(x)=1 si baza 
Sa se gaseasca aproximanta
continua pe [-1,1], pentru 
si baza formata din polinoamele Cebisev de
speta I
Sa se gaseasca aproximanta
continua pe [-1,1], pentru 
si baza formata din polinoamele Legendre.
Probleme facultative
Sa se gaseasca aproximanta discreta prin metoda celor mai mici patrate pentru ponderea w(x)=1 si baza formata din polinoamele Cebisev de speta I. Produsul scalar are forma
unde 
sunt radacinile polinomului Cebasev de speta I
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |
Vizualizari: 2172
Importanta: 
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved
