| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Functii
Generalitati
Definitie. Fie ![]() ,
, ![]() doua multimi nevide. Un element
doua multimi nevide. Un element ![]() din
din ![]() si un element
si un element ![]() din
din ![]() , luate in aceasta ordine formeaza un cuplu notat
, luate in aceasta ordine formeaza un cuplu notat ![]() .
.
In cuplul ![]() :
: ![]() se numeste primul element (sau prima
componenta sau abscisa) al
cuplului;
se numeste primul element (sau prima
componenta sau abscisa) al
cuplului; ![]() se numeste al doilea element (sau a doua componenta
sau ordonata) cuplului.
se numeste al doilea element (sau a doua componenta
sau ordonata) cuplului.
Doua cupluri ![]() si
si ![]() sunt egale si scriem
sunt egale si scriem ![]() .
.
Definitie. Fie ![]() ,
, ![]() doua multimi
nevide. Se numeste produsul
cartezian al multimii
doua multimi
nevide. Se numeste produsul
cartezian al multimii ![]() cu multimea
cu multimea ![]() , luate in aceasta ordine, multimea cuplurilor
avand prima componenta in
, luate in aceasta ordine, multimea cuplurilor
avand prima componenta in ![]() si a doua
componenta in
si a doua
componenta in ![]() .
.
Notatie.
Produsul cartezian al multimii ![]() cu multimea
cu multimea ![]() se noteaza :
se noteaza :
![]() .
.
Definitie. Fie ![]() ,
, ![]() doua multimi nevide. Spunem ca am definit o functie pe multimea
doua multimi nevide. Spunem ca am definit o functie pe multimea ![]() cu valori in
multimea
cu valori in
multimea ![]() daca printr-un
procedeu oarecare facem ca fiecarui element
daca printr-un
procedeu oarecare facem ca fiecarui element ![]() sa-i
corespunda un singur element
sa-i
corespunda un singur element ![]() .
.
Notatie. O
functie definita pe ![]() cu valori in
cu valori in ![]() se noteaza
se noteaza ![]() (citim "
(citim " ![]() definita pe
definita pe ![]() cu valori in
cu valori in ![]() ") sau
") sau ![]() . Uneori o functie se noteaza simbolic
. Uneori o functie se noteaza simbolic ![]() ,
, ![]() (citim "
(citim " ![]() de
de ![]() "), unde
"), unde ![]() este imaginea elementului
este imaginea elementului ![]() din
din ![]() sau valoarea
functiei
sau valoarea
functiei ![]() in
in ![]() . Elementul
. Elementul ![]() se numeste argument al functiei sau
variabila independenta.
se numeste argument al functiei sau
variabila independenta.
Elementele care definesc o functie sunt :
![]() domeniul de definitie ;
domeniul de definitie ;
![]() multimea de valori ale lui
multimea de valori ale lui ![]() sau codomeniul ;
sau codomeniul ;
legea ![]() care leaga cele
doua multimi.
care leaga cele
doua multimi.
Definitie. O
functie ![]() se numeste numerica daca
se numeste numerica daca ![]() .
.
Definitie. Fie ![]() o functie. Se
numeste graficul functiei
o functie. Se
numeste graficul functiei
![]() multimea de
cupluri
multimea de
cupluri ![]() .
.
Definitie. Fie ![]() ,
, ![]() doua
functii. Spunem ca functiile
doua
functii. Spunem ca functiile ![]() sunt egale (si scriem
sunt egale (si scriem ![]() ) daca :
) daca :
o
![]() (domeniile lor sunt
egale) ;
(domeniile lor sunt
egale) ;
o
![]() (codomeniile lor sunt
egale) ;
(codomeniile lor sunt
egale) ;
o
![]() (functiile
coincid in fiecare punct din domeniu).
(functiile
coincid in fiecare punct din domeniu).
Operatii cu functii
Fie ![]() o multime
nevida si
o multime
nevida si ![]() doua functii
reale.
doua functii
reale.
Functia ![]() definita prin
definita prin ![]() ,
, ![]() , se numeste suma
dintre functia
, se numeste suma
dintre functia ![]() si functia
si functia ![]() .
.
Functia ![]() definita prin
definita prin ![]() ,
, ![]() , se numeste produsul
functiilor
, se numeste produsul
functiilor ![]() si
si ![]() .
.
Functia ![]() definita prin
definita prin 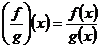 ,
, ![]() , unde
, unde ![]() ,
, ![]() , se numeste catul
(raportul) dintre functia
, se numeste catul
(raportul) dintre functia
![]() si functia
si functia ![]() .
.
Fie acum ![]() si
si ![]() . Functia
. Functia ![]() definita prin
definita prin ![]() ,
, ![]() , se numeste compusa
lui
, se numeste compusa
lui ![]() cu
cu ![]() .
.
Schema compunerii :
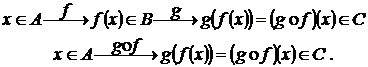
Observatie. Pentru doua functii are sens compunerea acestora numai daca codomeniul primei functii coincide cu domeniul celei de a doua.
Observatie.
Compunerea functiilor este asociativa, adica ![]() ,
, ![]() astfel incat sa
aiba sens compunerea acestora.
astfel incat sa
aiba sens compunerea acestora.
Exemple
1. Fie ![]() definite prin :
definite prin : ![]() ,
, ![]() . Sa se determine functiile
. Sa se determine functiile ![]() si
si ![]() .
.
Deoarece
codomeniul lui ![]() coincide cu domeniul
lui
coincide cu domeniul
lui ![]() (=
(=![]() ), are sens compunerea
), are sens compunerea ![]() .
.
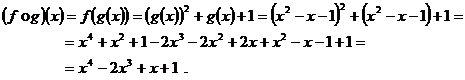
Deoarece codomeniul
lui ![]() coincide cu domeniul
lui
coincide cu domeniul
lui ![]() (=
(=![]() ), are sens compunerea
), are sens compunerea ![]() .
.
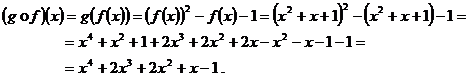
2. Fie ![]() definite prin :
definite prin : ![]() ,
, ![]() . Sa se determine
functiile
. Sa se determine
functiile ![]() si
si ![]() .
.
Deoarece codomeniul
lui ![]() coincide cu domeniul
lui
coincide cu domeniul
lui ![]() (=
(=![]() ), are sens compunerea
), are sens compunerea ![]() .
.
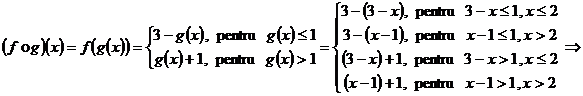
![]()
Deoarece codomeniul
lui ![]() coincide cu domeniul
lui
coincide cu domeniul
lui ![]() (=
(=![]() ), are sens compunerea
), are sens compunerea ![]() .
.
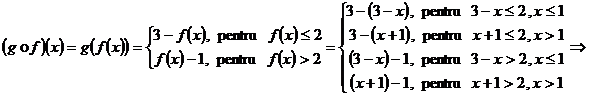
![]() .
.
Definitie.
Functia ![]() , definita prin
, definita prin ![]() ,
, ![]() , se numeste functia
identica a multimii
, se numeste functia
identica a multimii ![]() .
.
Observatie.
Daca ![]() este o functie
arbitrara, atunci
este o functie
arbitrara, atunci ![]() , iar daca
, iar daca ![]() este o functie
arbitrara, atunci
este o functie
arbitrara, atunci ![]() .
.
Definitie. Fie ![]() o functie. Se
numeste imaginea
functiei
o functie. Se
numeste imaginea
functiei ![]() multimea
notata cu
multimea
notata cu ![]() si egala cu
si egala cu ![]() . Uneori in loc de
. Uneori in loc de ![]() se scrie
se scrie ![]() . Se numeste preimaginea
functiei
. Se numeste preimaginea
functiei ![]() multimea
notata cu
multimea
notata cu ![]() si egala cu
si egala cu ![]() .
.
Observatie. ![]()
Exemple
1. Fie ![]() ,
, ![]() . Sa se determine
. Sa se determine ![]() .
.
Avem ![]() . Din
. Din ![]() rezulta
rezulta ![]() si deci
si deci ![]() . Cum
. Cum ![]() , rezulta
, rezulta ![]() . Deci
. Deci ![]() .
.
2. Fie ![]() ,
, ![]() . Sa se determine
. Sa se determine ![]() .
.
Fie ![]() . Deci exista
. Deci exista ![]() astfel incat
astfel incat ![]() , adica
, adica ![]() . De aici
. De aici ![]() si
si ![]() . Cum
. Cum ![]() se disting doua
cazuri :
se disting doua
cazuri :
Prin urmare, daca ![]() , atunci
, atunci ![]() . Deci
. Deci ![]() .
.
3. Se considera functia ![]() ,
, ![]() . Se cere
. Se cere ![]() .
.
Fie ![]() . Deci exista
. Deci exista ![]() astfel incat
astfel incat ![]() , adica
, adica ![]() . De aici
. De aici ![]() . Cum
. Cum ![]() rezulta
rezulta ![]() . De aici si
. De aici si ![]() rezulta
rezulta ![]() . Asadar
. Asadar ![]() .
.
Definitie. Fie ![]() si
si ![]() doua functii
cu proprietatile :
doua functii
cu proprietatile :
atunci ![]() se numeste prelungirea functiei
se numeste prelungirea functiei ![]() la
la ![]() , in timp ce
, in timp ce ![]() este numita restrictia lui
este numita restrictia lui ![]() la
la ![]() .
.
Definitie. O
multime ![]() se numeste simetrica in raport cu 0
(zero) daca pentru orice
se numeste simetrica in raport cu 0
(zero) daca pentru orice ![]() si
si ![]() .
.
Exemple :
Urmatoarele multimi sunt simetrice in raport cu 0 : ![]() ,
, ![]() ,
, ![]() ,
, ![]() , etc.
, etc.
Urmatoarele multimi nu sunt
simetrice in raport cu 0 : ![]() ,
, ![]() ,
, ![]() , etc.
, etc.
Definitie. Fie ![]() o multime
simetrica in raport cu zero. Functia
o multime
simetrica in raport cu zero. Functia ![]() se numeste para daca
se numeste para daca ![]() . Functia
. Functia ![]() se numeste impara daca
se numeste impara daca ![]() .
.
Observatie.
Graficul unei functii pare este simetric fata de axa ![]() , iar cel al unei functii impare este simetric in raport
cu originea O.
, iar cel al unei functii impare este simetric in raport
cu originea O.
Exemple
1. Sa se arate ca functia ![]() ,
, ![]() este para, in
timp ce functia
este para, in
timp ce functia ![]() ,
, ![]() .
.
Intr-adevar, avem : ![]() . Deci
. Deci ![]() este functie
para. Din
este functie
para. Din
![]() se deduce ca
se deduce ca ![]() este functie
impara.
este functie
impara.
2. Sa se arate ca functia ![]() ,
, ![]() nu este nici para
nici impara.
nu este nici para
nici impara.
Calculam ![]() . Pentru
. Pentru ![]() avem
avem ![]() , iar pentru
, iar pentru ![]()
Se obtine ![]() . Deci
. Deci ![]() . Prin urmare, nu pentru oricare
. Prin urmare, nu pentru oricare ![]() avem
avem ![]() sau
sau ![]() .
.
Observatie. Dupa cum am vazut mai sus, exista functii care nu sunt nici pare, nici impare .
Definitie. O
functie ![]() se numeste periodica daca
exista un numar real nenul
se numeste periodica daca
exista un numar real nenul ![]() astfel incat
astfel incat ![]() . Numarul
. Numarul ![]() se numeste perioada a functiei
se numeste perioada a functiei ![]() .
.
Daca printre numerele nenule pozitive ![]() exista un cel mai
mic numar pozitiv
exista un cel mai
mic numar pozitiv ![]() , atunci acesta se va numi perioada principala a functiei
, atunci acesta se va numi perioada principala a functiei ![]() .
.
Observatie.
Daca ![]() este perioada
pentru
este perioada
pentru ![]() , atunci orice numar de forma
, atunci orice numar de forma ![]() ,
, ![]() este de asemenea o
perioada pentru
este de asemenea o
perioada pentru ![]() .
.
Exemplu :
Functia ![]() ,
, ![]() este periodica,
de perioada principala
este periodica,
de perioada principala ![]() .
.
Monotonia functiilor
A studia monotonia unei functii ![]() revine la a preciza :
revine la a preciza :
Definitie. Fie ![]() o functie de
variabila reala si
o functie de
variabila reala si ![]() .
.
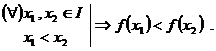
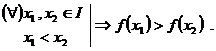
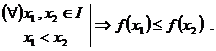
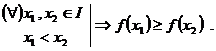
Observatie. O
functie ![]() strict
crescatoare pe
strict
crescatoare pe ![]() sau strict
descrescatoare pe
sau strict
descrescatoare pe ![]() se numeste functie
strict monotona pe
se numeste functie
strict monotona pe ![]() . O functie
. O functie ![]() crescatoare pe
crescatoare pe ![]() sau
descrescatoare pe
sau
descrescatoare pe ![]() se numeste monotona
pe
se numeste monotona
pe ![]() . Daca
. Daca ![]() este strict
monotona (sau monotona) pe
este strict
monotona (sau monotona) pe ![]() (pe tot domeniul de
definitie) spunem simplu ca
(pe tot domeniul de
definitie) spunem simplu ca ![]() este strict
monotona (sau monotona) fara a mai indica multimea.
este strict
monotona (sau monotona) fara a mai indica multimea.
Teorema. Fie ![]() o functie
numerica si
o functie
numerica si ![]() . Atunci :
. Atunci :
Observatie. Demonstratia
teoremei precedente rezulta direct din definitie. Raportul ![]() se mai numeste
raportul de variatie asociat lui
se mai numeste
raportul de variatie asociat lui ![]() si numerelor
si numerelor ![]() .
.
Observatie.
Folosind cunostintele de analiza matematica, teorema
precedenta se poate reformula : Daca
prima derivata a functiei ![]() este strict
pozitiva, atunci functia este strict crescatoare, daca
prima derivata a functiei
este strict
pozitiva, atunci functia este strict crescatoare, daca
prima derivata a functiei ![]() este strict
negativa, atunci functia este strict descrescatoare.
este strict
negativa, atunci functia este strict descrescatoare.
Observatie. O
functie monotona pe o multime ![]() , ramane monotona pe orice submultime a sa.
, ramane monotona pe orice submultime a sa.
Exemple
1. Functia
de gradul intai ![]() ,
, ![]() .
.
Daca ![]() , atunci
, atunci ![]() este strict
crescatoare, deoarece, daca
este strict
crescatoare, deoarece, daca ![]() ,
, ![]() , atunci :
, atunci :
![]() si conform
teoremei precedente, functia este strict crescatoare.
si conform
teoremei precedente, functia este strict crescatoare.
Daca ![]() , atunci
, atunci ![]() este strict
crescatoare, deoarece, daca
este strict
crescatoare, deoarece, daca ![]() ,
, ![]() , atunci :
, atunci :
![]() si conform
teoremei precedente, functia este strict descrescatoare.
si conform
teoremei precedente, functia este strict descrescatoare.
2. Functia
de gradul doi ![]() ,
, ![]() ,
, ![]() ,
, ![]() 0. Intervalele de monotonie ale aceste functii sunt :
0. Intervalele de monotonie ale aceste functii sunt : ![]() ,
,![]() .
.
Daca ![]() , atunci monotonia lui
, atunci monotonia lui ![]() este indicata in
tabelul :
este indicata in
tabelul :
|
|
|
|
|
descrescatoare |
Daca ![]() , atunci monotonia lui
, atunci monotonia lui ![]() este indicata in
tabelul :
este indicata in
tabelul :
|
|
|
|
|
crescatoare |
3. Functia
putere cu exponent natural ![]() ,
, ![]() ,
, ![]() .
.
Daca ![]() este par, atunci
monotonia lui
este par, atunci
monotonia lui ![]() este indicata in
tabelul :
este indicata in
tabelul :
|
|
|
|
|
descrescatoare 0 crescatoare |
Daca ![]() este impar, atunci
monotonia lui
este impar, atunci
monotonia lui ![]() este indicata in
tabelul :
este indicata in
tabelul :
|
|
|
|
|
crescatoare 0 crescatoare |
Observatie.
Daca o functie ![]() este strict
crescatoare pe
este strict
crescatoare pe ![]() si pe
si pe ![]() , nu rezulta neaparat ca este strict
crescatoare pe
, nu rezulta neaparat ca este strict
crescatoare pe ![]() (adica pe tot
domeniul). De exemplu, fie
(adica pe tot
domeniul). De exemplu, fie ![]() , definita prin
, definita prin ![]() . Cum functiile
. Cum functiile ![]() ,
, ![]() ,
, ![]() ,
, ![]() sunt strict
crescatoare pe
sunt strict
crescatoare pe ![]() , atunci ele raman la fel si pe intervalele
, atunci ele raman la fel si pe intervalele ![]() si respectiv
si respectiv ![]() . Deci
. Deci ![]() este strict
crescatoare pe
este strict
crescatoare pe ![]() ,
, ![]() , fara a fi strict crescatoare pe
, fara a fi strict crescatoare pe ![]() , deoarece pentru
, deoarece pentru ![]() avem
avem ![]() .
.
Conditiile ce ar trebui verificate pentru
ca functia sa fie strict crescatoare pe ![]() sunt :
sunt :
Observatie. Un alt mod de a studia monotonia este acela de a utiliza graficul.
Definitie.
Daca exista ![]() astfel incat
astfel incat ![]() ,
, ![]() , atunci
, atunci ![]() se numeste maximul functiei
se numeste maximul functiei ![]() pe multimea
pe multimea ![]() si scriem
si scriem ![]() . Punctul
. Punctul ![]() pentru care se
obtine valoarea maxima a lui
pentru care se
obtine valoarea maxima a lui ![]() pe
pe ![]() se numeste punct de maxim pentru
functia
se numeste punct de maxim pentru
functia ![]() pe
pe ![]() .
.
Definitie.
Daca exista ![]() astfel incat
astfel incat ![]() ,
, ![]() , atunci
, atunci ![]() se numeste minimul functiei
se numeste minimul functiei ![]() pe multimea
pe multimea ![]() si scriem
si scriem ![]() . Punctul
. Punctul ![]() pentru care se
obtine valoarea minima a lui
pentru care se
obtine valoarea minima a lui ![]() pe
pe ![]() se numeste punct de minim pentru
functia
se numeste punct de minim pentru
functia ![]() pe
pe ![]() .
.
Definitie.
Valoarea maxima sau minima a lui ![]() pe
pe ![]() se numeste valoare extrema a
functiei
se numeste valoare extrema a
functiei ![]() pe
pe ![]() . Punctul
. Punctul ![]() de maxim sau
de maxim sau ![]() de minim se
numeste punct de extrem
pentru functia
de minim se
numeste punct de extrem
pentru functia ![]() pe
pe ![]() .
.
Definitie. O
functie numerica ![]() se numeste marginita, daca
exista doua numere reale
se numeste marginita, daca
exista doua numere reale ![]() astfel incat
astfel incat ![]() ,
, ![]() .
.
Observatie.
Semnificatia geometrica a unei functii marginite este
ca aceea ca graficul functiei este cuprins intre dreptele
orizontale ![]() ,
, ![]() .
.
Operatii cu functii strict monotone
Teorema. Fie ![]() doua
functii.
doua
functii.
Daca ![]() sunt strict
crescatoare (strict descrescatoare), atunci
sunt strict
crescatoare (strict descrescatoare), atunci ![]() este strict
crescatoare (strict descrescatoare). (Suma a doua functii strict crescatoare (strict
descrescatoare) este o functie strict crescatoare (strict
descrescatoare)).
este strict
crescatoare (strict descrescatoare). (Suma a doua functii strict crescatoare (strict
descrescatoare) este o functie strict crescatoare (strict
descrescatoare)).
Daca ![]() sunt strict
crescatoare (sau strict descrescatoare), atunci
sunt strict
crescatoare (sau strict descrescatoare), atunci ![]() este strict
crescatoare. (Compunerea a doua
functii de aceeasi monotonie da o functie strict
crescatoare).
este strict
crescatoare. (Compunerea a doua
functii de aceeasi monotonie da o functie strict
crescatoare).
Daca ![]() au monotonii diferite,
atunci
au monotonii diferite,
atunci ![]() este strict
descrescatoare.
este strict
descrescatoare.
Definitie. Fie
functia ![]() ,
, ![]() interval. Se spune
ca functia
interval. Se spune
ca functia ![]() este convexa pe
este convexa pe ![]() , daca
, daca ![]() si
si ![]() ,
, ![]() , avem :
, avem :
![]() .
.
Functia ![]() se numeste conacava pe
se numeste conacava pe ![]() ,daca
,daca ![]() si
si ![]() ,
, ![]() , avem :
, avem :
![]() .
.
Exemplu
Functia
de gradul al doilea, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 0.
0.
Daca ![]() , atunci
, atunci ![]() este convexa .
este convexa .
Daca ![]() , atunci
, atunci ![]() este concava .
este concava .
Observatie. Interpretarea geometrica a concavitatii si convexitatii :

In limbaj trivial spunem despre graficul functiei convexe ca " tine apa " in timp ce graficul functiei concave " nu tine apa ".
Injectivitate, surjectivitate, bijectivitate
Definitie. Fie o
functie ![]() , unde
, unde ![]() . Functia
. Functia ![]() se numeste injectiva, daca
si numai daca :
se numeste injectiva, daca
si numai daca :
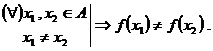
Propozitie. ![]() este injectiva
este injectiva 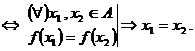
Observatie. In exercitii, pentru a proba ca o functie este injectiva, este mai practic sa se foloseasca propozitia precedenta.
Propozitie. Orice functie strict monotona este injectiva.
Observatie. Foloind cunostintele de analiza matematica, propozitia precedenta se poate reformula astfel : O functie a carei derivata este strict pozitiva sau strict negativa este injectiva.
Propozitie.
Daca ![]() si
si ![]() sunt doua
functii injective, atunci
sunt doua
functii injective, atunci ![]() este o functie
injectiva. (Compunerea a doua
functii injective este tot o functie injectiva).
este o functie
injectiva. (Compunerea a doua
functii injective este tot o functie injectiva).
Propozitie.
Functia ![]() este injectiva
daca : pentru orice
este injectiva
daca : pentru orice ![]() (codomeniului),
ecuatia
(codomeniului),
ecuatia ![]() are cel mult o
solutie.
are cel mult o
solutie.
Observatie. Folosind
graficul functiei ![]() , putem stabili injectivitatea astfel : Daca
, putem stabili injectivitatea astfel : Daca
orice paralela ![]() dusa prin un punct
al codomeniului la axa
dusa prin un punct
al codomeniului la axa ![]() intersecteaza
graficul in cel mult un punct, atunci functia este injectiva. Functia nu este injectiva, daca exista cel putin o
paralela dusa prin un punct al codomeniului la axa
intersecteaza
graficul in cel mult un punct, atunci functia este injectiva. Functia nu este injectiva, daca exista cel putin o
paralela dusa prin un punct al codomeniului la axa ![]() care
intersecteaza graficul in cel putin doua puncte.
care
intersecteaza graficul in cel putin doua puncte.
Exemple
1. Sa se arate ca functia de
gradul intai ![]() ,
, ![]() este injectiva.
este injectiva.
Metoda
1. Folosim prima propozitie : Fie ![]() (domeniului), astfel incat
(domeniului), astfel incat ![]() si deci
functia este injectiva.
si deci
functia este injectiva.
Metoda 2. Ne folosim de monotonia functiei de gradul intai :
Metoda 3. Folosim graficul functiei de gradul intai :
Dupa cum stim din clasa a-VII-a,
garficul functiei de gradul intai este o dreapta, care nu este
paralela cu axa ![]() (ar fi paralela
cu axa
(ar fi paralela
cu axa ![]() numai in cazul in care
numai in cazul in care
![]() , exclus in cazul functiei de gradul intai) si deci
orice paralela la axa
, exclus in cazul functiei de gradul intai) si deci
orice paralela la axa ![]() poate intersecta
graficul functiei in exact un punct.
poate intersecta
graficul functiei in exact un punct.
2. Sa se studieze injectivitatea
functiei ![]() ,
, 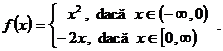
Metoda
1. Fie ![]() cu
cu ![]()
![]() , intrucat
, intrucat 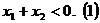
Fie ![]() cu
cu ![]()
Fie ![]() si
si ![]() , evident
, evident ![]() . Sa analizam imaginile acestor argumente :
. Sa analizam imaginile acestor argumente :
![]() ,
, ![]() , adica
, adica ![]()
Din ![]() si
si ![]() rezulta ca
rezulta ca ![]() este injectiva.
este injectiva.
Metoda
2. Se arata ca ![]() este strict
descrescatoare, considerand de asemenea cele trei cazuri.
este strict
descrescatoare, considerand de asemenea cele trei cazuri.
Metoda 3. Este metoda verificarii dupa trasarea graficului .
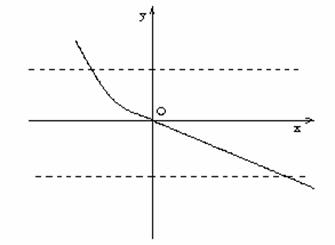
Dupa cum se vede
in figura din stanga, orice paralela (doua dintre ele au fost trasate
punctat) dusa prin un punct al codomeniului la axa ![]() , intersecteaza graficul functiei in exact un
punct, deci functia
, intersecteaza graficul functiei in exact un
punct, deci functia ![]() este injectiva .
este injectiva .
3. Aratati ca functia ![]() ,
, ![]() nu este
injectiva.
nu este
injectiva.
Pentru a demonstra ca aceasta
functie nu este injectiva vom utiliza ultima propozitie. Aceasta
se traduce in cazul nostru prin : Pentru orice valoare ![]() (din codomeniu), ecuatia
(din codomeniu), ecuatia ![]() are cel mult o
solutie , adica
are cel mult o
solutie , adica ![]() , ecuatia
, ecuatia ![]() are cel mult o
solutie. Fie
are cel mult o
solutie. Fie ![]() , atunci ecuatia se scrie
, atunci ecuatia se scrie ![]()
![]() care admite
solutiile distincte
care admite
solutiile distincte ![]() si conform
ultimei propozitii rezulta ca functia nu este
injectiva .
si conform
ultimei propozitii rezulta ca functia nu este
injectiva .
Definitie. Fie o
functie ![]() , unde
, unde ![]() . Functia
. Functia ![]() se numeste surjectiva daca pentru
orice
se numeste surjectiva daca pentru
orice ![]() (codomeniului), exista cel putin un element
(codomeniului), exista cel putin un element ![]() (domeniului) astfel
incat
(domeniului) astfel
incat ![]() .
.
Observatie.
Elementul ![]() care apare in definitie
se obtine rezolvand ecuatia
care apare in definitie
se obtine rezolvand ecuatia ![]() .
.
Propozitie.
Functia ![]() este surjectiva
daca : pentru orice
este surjectiva
daca : pentru orice ![]() (codomeniului),
ecuatia
(codomeniului),
ecuatia ![]() are cel putin o
solutie
are cel putin o
solutie ![]() .
.
Observatie.
Folosind graficul unei functii ![]() , putem stabili surjectivitatea acesteia astfel : Daca
orice paralela
, putem stabili surjectivitatea acesteia astfel : Daca
orice paralela ![]() dusa prin un
punct al codomeniului la axa
dusa prin un
punct al codomeniului la axa ![]() intersecteaza graficul in cel putin
un punct, atunci functia este
surjectiva. Functia
intersecteaza graficul in cel putin
un punct, atunci functia este
surjectiva. Functia ![]() nu este surjectiva, daca exista cel putin o
paralela dusa prin un punct al codomeniului la axa
nu este surjectiva, daca exista cel putin o
paralela dusa prin un punct al codomeniului la axa ![]() care nu
intersecteaza graficul in nici un punct.
care nu
intersecteaza graficul in nici un punct.
Propozitie.
Daca ![]() ,
, ![]() sunt doua
functii surjective, atunci si functia
sunt doua
functii surjective, atunci si functia ![]() este surjectiva .
(Compunerea a doua functii surjective este tot o functie
surjectiva).
este surjectiva .
(Compunerea a doua functii surjective este tot o functie
surjectiva).
Propozitie. O functie este surjectiva, daca codomeniul coincide cu imaginea functiei prin domeniul de definitie.
Exemple
1. Sa se arate ca functia de
gradul intai ![]() ,
, ![]() este surjectiva.
este surjectiva.
Conform definitiei, vrem sa
aratam ca pentru orice ![]() (codomeniului)
exista cel putin un
(codomeniului)
exista cel putin un ![]() (domeniului), astfel
incat
(domeniului), astfel
incat ![]() . Fie pentru aceasta
. Fie pentru aceasta ![]() astfel incat
astfel incat ![]()
![]()
![]() si cum
si cum ![]() rezulta ca
pentru
rezulta ca
pentru ![]() , exista un
, exista un ![]() , astfel incat
, astfel incat ![]() . In concluzie, conform definitiei rezulta ca
functia este surjectiva.
. In concluzie, conform definitiei rezulta ca
functia este surjectiva.
2. Sa se studieze surjectivitatea
functiei ![]() ,
, 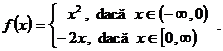
Metoda
1. Deoarece ![]() si
si ![]() , rezulta ca imaginea functiei este
, rezulta ca imaginea functiei este ![]() , cu alte cuvinte
, cu alte cuvinte ![]() si conform
ultimei propozitii, functia este surjectiva.
si conform
ultimei propozitii, functia este surjectiva.
Metoda
2. Fie ![]() , atunci
, atunci ![]() si deci
si deci ![]() , adica ecuatia
, adica ecuatia ![]() are solutii in
domeniu.
are solutii in
domeniu. ![]()
Fie ![]() , atunci
, atunci ![]() si cum
si cum ![]() , adica ecuatia
, adica ecuatia ![]() are si in acest
caz solutie in domeniu.
are si in acest
caz solutie in domeniu. ![]()
Din ![]() si
si ![]() rezulta ca
rezulta ca ![]() este surjectiva .
este surjectiva .
Metoda 3. Este metoda grafica .
3. Sa se arate ca functia ![]() ,
, 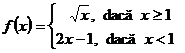 este surjectiva.
este surjectiva.
Aratam ca ecuatia in ![]() ,
, ![]() ,
, ![]() are cel putin o
radacina reala. Distingem doua cazuri :
are cel putin o
radacina reala. Distingem doua cazuri :
![]() , ecuatia este
, ecuatia este ![]() . Membrul stang
. Membrul stang ![]() fiind pozitiv, se
impune
fiind pozitiv, se
impune ![]() . Din
. Din ![]() . Cum
. Cum ![]() , care coroborat cu
, care coroborat cu ![]() da
da ![]() . Asadar pentru
. Asadar pentru ![]() , exista
, exista ![]() astfel incat
astfel incat ![]() .
. ![]()
![]() , ecuatia este
, ecuatia este ![]() cu solutia
cu solutia ![]() . Din
. Din ![]() rezulta
rezulta ![]() , adica
, adica ![]() . Deci pentru
. Deci pentru ![]() , exista
, exista ![]() astfel incat
astfel incat ![]() .
. ![]()
Din ![]() si
si ![]() rezulta ca
rezulta ca ![]() , exista
, exista ![]() astfel incat
astfel incat ![]() , ceea ce arata ca
, ceea ce arata ca ![]() este surjectiva.
este surjectiva.
4. Sa se arate ca functia ![]() ,
, 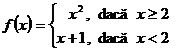 nu este surjectiva.
nu este surjectiva.
Metoda 1. Utilizam graficul functiei .
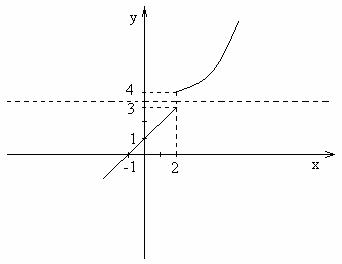 Trasam graficul functiei (vezi figura din stanga) si
constatam ca o paralela la axa
Trasam graficul functiei (vezi figura din stanga) si
constatam ca o paralela la axa ![]() dusa printr-un
punct din intervalul
dusa printr-un
punct din intervalul ![]() al codomeniului nu
taie graficul in nici un punct .
al codomeniului nu
taie graficul in nici un punct .
Metoda
2. Aratam ca ecuatia ![]() nu are solutii
pentru orice
nu are solutii
pentru orice ![]() . Analizam cele doua cazuri date de definitia
functiei :
. Analizam cele doua cazuri date de definitia
functiei :
![]() , ecuatia este
, ecuatia este ![]() . Se impune
. Se impune ![]() , unde
, unde ![]() . Cum
. Cum ![]() rezulta ca
rezulta ca ![]() , adica
, adica ![]() . Deci pentru
. Deci pentru ![]() , exista
, exista ![]() astfel incat
astfel incat ![]() .
. ![]()
![]() , ecuatia este
, ecuatia este ![]() , care are solutia
, care are solutia ![]() . Din
. Din ![]() se deduce
se deduce ![]() . Deci pentru
. Deci pentru ![]() , exista
, exista ![]() , astfel incat
, astfel incat ![]() .
. ![]()
Din ![]() si
si ![]() se vede ca numai
pentru
se vede ca numai
pentru ![]() si
si ![]() ecuatia are
solutie. Daca
ecuatia are
solutie. Daca ![]() , ecuatia nu mai are solutii, deci functia nu
este surjectiva.
, ecuatia nu mai are solutii, deci functia nu
este surjectiva.
Definitie. Fie o
functie ![]() , unde
, unde ![]() . Functia
. Functia ![]() se numeste bijectiva daca este
atat injectiva cat si surjectiva.
se numeste bijectiva daca este
atat injectiva cat si surjectiva.
Propozitie.
Functia ![]() este bijectiva
daca : pentru orice
este bijectiva
daca : pentru orice ![]() (codomeniului),
ecuatia
(codomeniului),
ecuatia ![]() are exact o
solutie
are exact o
solutie ![]() .
.
Observatie.
Folosind graficul unei functii ![]() , putem stabili bijectivitatea acesteia astfel : Daca
orice paralela
, putem stabili bijectivitatea acesteia astfel : Daca
orice paralela ![]() dusa prin un
punct al codomeniului la axa
dusa prin un
punct al codomeniului la axa ![]() intersecteaza
graficul in exact un punct, atunci functia este bijectiva. Functia
intersecteaza
graficul in exact un punct, atunci functia este bijectiva. Functia ![]() nu este bijectiva, daca exista cel putin o
paralela dusa prin un punct al codomeniului la axa
nu este bijectiva, daca exista cel putin o
paralela dusa prin un punct al codomeniului la axa ![]() care nu
intersecteaza graficul in nici un punct sau il intesecteaza in mai
multe puncte .
care nu
intersecteaza graficul in nici un punct sau il intesecteaza in mai
multe puncte .
Exemple de functii bijective
Propozitie.
Daca ![]() ,
, ![]() sunt doua
functii bijective, atunci si functia
sunt doua
functii bijective, atunci si functia ![]() este bijectiva. (Compunerea a doua functii
bijective este tot o functie bijectiva).
este bijectiva. (Compunerea a doua functii
bijective este tot o functie bijectiva).
Definitie. O
functie ![]() se numeste inversabila daca
exista o functie
se numeste inversabila daca
exista o functie ![]() astfel incat :
astfel incat : ![]() si
si ![]() . Functia
. Functia ![]() din definitie se
numeste inversa functiei
din definitie se
numeste inversa functiei ![]() si se
noteaza
si se
noteaza ![]() .
.
Teorema. O
functie ![]() este inversabila
daca si numai daca este bijectiva.
este inversabila
daca si numai daca este bijectiva.
Observatie.
Practic, inversa lui ![]() se determina prin
rezolvarea ecuatiei in
se determina prin
rezolvarea ecuatiei in ![]() ,
, ![]() ,
, ![]() . Solutia unica
. Solutia unica ![]() ,
, ![]() precizeaza
inversa lui
precizeaza
inversa lui ![]() .
.
Propozitie. Fie ![]() o functie
bijectiva si strict crescatoare (strict descrescatoare).
o functie
bijectiva si strict crescatoare (strict descrescatoare).
Atunci ![]() este de asemenea,
strict crescatoare (strict descrescatoare).
este de asemenea,
strict crescatoare (strict descrescatoare).
Exemple
1. Sa se determine inversa functiei
de gradul intai ![]() ,
, ![]() .
.
Atat injectivitatea cat si surjectivitatea functiei de gradul intai au fost demonstrate mai sus. Functia fiind bijectiva, conform teoremei precedente, admite inversa.
Conform observatiei, inversa este precizata
de solutia ecuatiei in ![]() ,
, ![]() . Deci inversa este data de
. Deci inversa este data de ![]() . Inversa este
. Inversa este ![]() . Trecand la variabila
. Trecand la variabila ![]() , putem scrie
, putem scrie ![]() .
.
2. Fie functia ![]() definita prin
definita prin 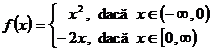 . Sa se arate ca
. Sa se arate ca ![]() este bijectiva
si sa se calculeze inversa
este bijectiva
si sa se calculeze inversa ![]() .
.
Bijectivitatea (injectivitatea + surjectivitatea) functiei a fost demonstrata mai sus. Pentru determinarea functiei inverse, avem :
![]() , cu
, cu ![]() , cu
, cu ![]() .
.
![]() , cu
, cu ![]() , cu
, cu ![]() . In final rezulta deci
. In final rezulta deci 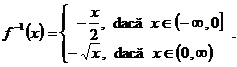
Exercitii propuse
1. Fie aplicatia "![]() " prin care, fiecarui cetatean roman
(nascut pe teritpriul Romaniei) ii corespunde localitatea sa natala
si aplicatia "
" prin care, fiecarui cetatean roman
(nascut pe teritpriul Romaniei) ii corespunde localitatea sa natala
si aplicatia "![]() " care face ca fiecarei localitati sa-i corespunda
codul sau postal.
" care face ca fiecarei localitati sa-i corespunda
codul sau postal.
2. Fie ![]() si
si ![]() , o functie care indeplineste conditiile :
, o functie care indeplineste conditiile :
a)
Sa se determine ![]() si functia
de gradul intai care verifica conditiile 1), 2).
si functia
de gradul intai care verifica conditiile 1), 2).
b)
Sa se arate ca singura
functie ![]() care verifica
conditiile 1), 2) este functia gasita la punctul a).
care verifica
conditiile 1), 2) este functia gasita la punctul a).
3. Fie functia ![]() ,
, ![]() , unde
, unde ![]() . Sa se detremine :
. Sa se detremine :
![]() .
.
4. Fie functiile ![]() ,
, ![]() si
si ![]() ,
, ![]() . Sa se determine
. Sa se determine ![]() si
si ![]() .
.
5. Fie functia ![]() ,
, ![]() . Sa se arate ca
. Sa se arate ca ![]() este inversabila
si sa se determine
este inversabila
si sa se determine ![]() .
.
6. Sa se arate ca functia ![]() , definita prin
, definita prin ![]() admite restrictii
inversabile definite pe :
admite restrictii
inversabile definite pe :
i) ![]() ; ii)
; ii)
![]() ; iii)
; iii) 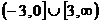 .
.
7. Sa se demonstreze ca urmatoarele functii sunt injective :
a)
![]() ,
, ![]()
b)
![]() ,
, ![]() .
.
8. Sa se determine imaginea urmatoarelor functii :
a)
![]() ,
, ![]() ;
;
b)
![]() ,
, ![]() ;
;
c)
![]() ,
, ![]() ;
;
d) ![]() ,
, ![]() .
.
9. Fie functiile ![]() si
si ![]() definite prin :
definite prin :
a) 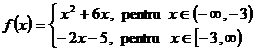 ,
, ![]()
b) 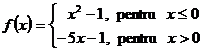 ,
, ![]() .
.
Sa se calculeze ![]() si
si ![]() .
.
10. Fie ![]() , unde
, unde ![]() este o multime
finita. Sa se arate ca urmatoarele afirmatii sunt
echivalente
este o multime
finita. Sa se arate ca urmatoarele afirmatii sunt
echivalente
a)
![]() este injectiva ;
este injectiva ;
b)
![]() este surjectiva ;
este surjectiva ;
c)
![]() este bijectiva .
este bijectiva .
11. Fie ![]() ,
, ![]() doua
functii. Sa se arate ca daca
doua
functii. Sa se arate ca daca
a)
![]() este injectiva,
atunci
este injectiva,
atunci ![]() este injectiva ;
este injectiva ;
b)
![]() este surjectiva, atunci
este surjectiva, atunci ![]() este surjectiva
este surjectiva
c)
![]() este bijectiva, atunci
este bijectiva, atunci ![]() este injectiva,
iar
este injectiva,
iar ![]() este surjectiva ;
este surjectiva ;
d)
![]() este injectiva, iar
este injectiva, iar ![]() este surjectiva ,
atunci
este surjectiva ,
atunci ![]() este injectiva .
este injectiva .
12. Sa se arate,
folosind graficul, ca functia ![]() ,
, 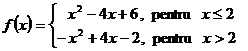 este bijectiva
si sa se determine
este bijectiva
si sa se determine ![]() .
.
13. Sa se arate ca urmatoarele functii nu sunt injective :
a)
![]() ,
, ![]() ;
;
b)
![]() ,
, ![]() ;
;
c)
![]() ,
, ![]() ;
;
d) ![]() ,
, ![]() .
.
14. Fie functia ![]() de forma :
de forma :
![]() .
.
a)
Sa se determine ![]() astfel incat graficul
functiei sa treaca prin punctul
astfel incat graficul
functiei sa treaca prin punctul ![]() .
.
b)
Sa se cerceteze daca
functia ![]() este injectiva .
este injectiva .
15. Pentru orice ![]() se considera
functia
se considera
functia
![]() ,
, ![]() . Sa se determine valorile lui
. Sa se determine valorile lui ![]() si
si ![]() pentru care
pentru care ![]() este :
este :
a) injectiva b) surjectiva c) bijectiva .
16. Fie functia ![]() , definita prin
, definita prin 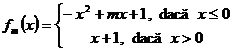 unde
unde ![]() este un parametru
real. Sa se determine valorile lui
este un parametru
real. Sa se determine valorile lui ![]() pentru care
pentru care ![]() este surjectiva,
injectiva, respectiv inversabila. In cazul in care
este surjectiva,
injectiva, respectiv inversabila. In cazul in care ![]() este inversabila,
sa se determine inversa functiei
este inversabila,
sa se determine inversa functiei ![]() .
.
17. Se considera functia ![]() care verifica
relatia :
care verifica
relatia : ![]() ,
, ![]() si
si ![]() . Sa se arate ca
. Sa se arate ca ![]() este functie
periodica de perioada 4.
este functie
periodica de perioada 4.
18. Sa se arate ca functia ![]() ,
, ![]() , este impara.
, este impara.
19. Sa se determine ![]() , astfel incat
, astfel incat
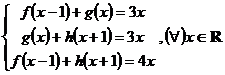 .
.
20. Exista functii ![]() cu proprietatea
cu proprietatea
![]() ,
, ![]() ?
?
21. Fie functiile ![]() , unde
, unde ![]() si
si ![]() . Sa se arate ca
. Sa se arate ca ![]() nu este
injectiva, iar
nu este
injectiva, iar ![]() este injectiva .
este injectiva .
22. Fie functia ![]() ,
, ![]() . Sa se determine
. Sa se determine ![]() si
si ![]() astfel incat
astfel incat ![]() .
.
23. Fie functia ![]() ,
, ![]() ,
, ![]() . Sa se determine valorile lui
. Sa se determine valorile lui ![]() astfel incat
astfel incat 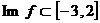 .
.
24. Fie functiile ![]() definite prin
definite prin
![]() ;
; ![]() .
.
Sa se determine functiile : ![]()
25. Sa se
determine functiile ![]() care satisfac
relatia :
care satisfac
relatia : ![]() .
.
26. Fie functia ![]() ,
, 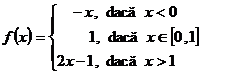 .
.
a)
Sa se
determine functiile ![]() si
si ![]() si
verificati egalitatea
si
verificati egalitatea ![]() ;
;
b)
Studiati paritatea
functiilor ![]() .
.
27. Utilizand metoda grafica sa se precizeze care din functiile de mai jos sunt bijective :
a)
![]() ,
, ![]() ;
;
b)
![]() ,
, ![]()
28. Daca ![]() ,
, ![]() sa se arate
ca functia
sa se arate
ca functia ![]() definita prin
definita prin 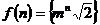 este injectiva
(s-a notat
este injectiva
(s-a notat ![]() ).
).
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 27368
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved