| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Caracteristici numerice asociate variabilelor aleatoare
Definitia 1 Fie variabila aleatoare X de tip discret, avand distributia 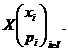 Numim valoare medie
(speranta matematica ), caracteristica numerica
Numim valoare medie
(speranta matematica ), caracteristica numerica
![]()
Observatia 2. Daca variabila aleatoare X este simpla, adica are un numar finit de valori, atunci valoarea medie exista.
Daca multimea de indici I este infinit numarabila, valoarea medie exista cand seria care o defineste este absolut convergenta.
Exemplul 3 Fie variabila aleatoare X ce urmeaza legea binomiala, adica are distributia
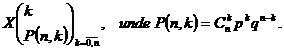
Pentru a calcula valoarea medie a variabilei aleatoare X, scriem succesiv
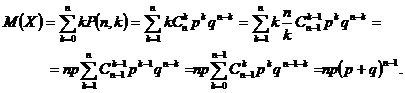
In sirul de egalitati
scrise, s-a folosit formula de recurenta pentru numarul de
combinari ![]() si formula
binomului lui Newton. Daca se tine
seama de faptul ca
si formula
binomului lui Newton. Daca se tine
seama de faptul ca ![]() rezulta ca
rezulta ca ![]()
Exemplul 4 Se considera variabila aleatoare X ce urmeaza legea lui Poisson, adica are distributia
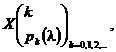 unde
unde ![]()
Putem scrie succesiv
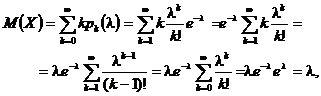
deci ![]()
Propozitia 5 Valoarea medie poseda urmatoarele proprietati:
![]()
![]()
daca variabilele aleatoare X si Y sunt independente, atunci
![]()
Demonstratie Vom considera variabilele aleatoare X si Y de tip discret cu distributiile
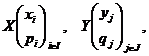
pentru care exista ![]() si
si ![]()
(1) Scriem succesiv
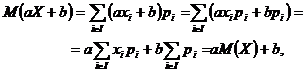
de unde ![]()
(2) Daca
variabilele aleatoare X si Y au distributiile, precizate mai
sus, atunci variabila aleatoare ![]() are distributia
are distributia
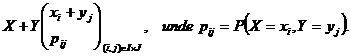
Prin urmare, avem ca
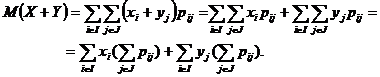
Tinand seama de Observatia 3.24, se obtine ca
![]()
Avand in vedere ca variabilele aleatoare X si Y sunt independente, se obtine distributia variabilei aleatoare produs
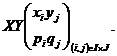
Asadar, putem scrie sucesiv
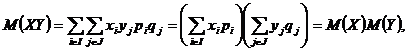
adica ![]()
Observatia 6 Daca in propozitia precedenta,
la punctul (1) se ia ![]() , atunci se obtine ca valoarea medie a unei
constante este constanta insasi, iar punctele (2) si (3) se pot
extinde pentru un numar finit de variabile aleatoare.
, atunci se obtine ca valoarea medie a unei
constante este constanta insasi, iar punctele (2) si (3) se pot
extinde pentru un numar finit de variabile aleatoare.
Definitia 7. Numim valoare medie (speranta matematica) pentru variabiala aleatoare X de tip continuu, caracteristica numerica
![]()
Exemplul 8 Fie variabila aleatoare X ce urmeaza legea uniforma pe intervalul ![]() , adica are densitatea de probabilitate
, adica are densitatea de probabilitate
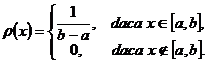
Valoarea medie a variabilei aleatoare X va fi
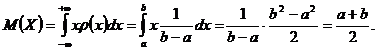
Exemplul 9. Daca variabila aleatoare X urmeaza legea normala ![]() , atunci are densitatea de probabilitate
, atunci are densitatea de probabilitate
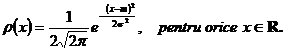
Pentru aceasta variabila
aleatoare, facand schimbarea de variabila ![]() avem ca
avem ca
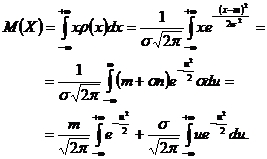
A doua integrala este zero, deoarece
functia ce se integreaza este o functie impara, iar
intervalul de integrare este simetric fata de origine. Prima
integrala se cunoaste ca este ![]() . Prin urmare avem ca
. Prin urmare avem ca ![]()
Propozitia 10. Valoarea medie poseda urmatoarele proprietati:
(1) ![]()
(2) ![]()
(3) daca variabilele aleatoare X si Y sunt independente, atunci ![]()
Demonstratie. (1) Daca notam prin ![]() atunci, conform Aplicatiaiei
3.69, avem
atunci, conform Aplicatiaiei
3.69, avem
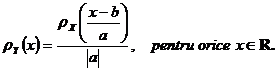
Putem scrie, prin urmare, ca
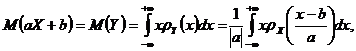
de unde prin schimbrea de variabila ![]() se obtine
succesiv
se obtine
succesiv
![]()
deci ![]()
(2) Daca notam prin ![]() care are densitatea de
probabilitate
care are densitatea de
probabilitate ![]() , iar densitatea de probabilitate a vectorului aleator
, iar densitatea de probabilitate a vectorului aleator ![]() o notam prin
o notam prin ![]() , atunci
, atunci
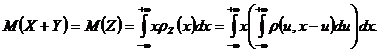
Facem schimbarea ordinei de integrare, iar
apoi efectuam schimbarea de variabila ![]() si obtinem
si obtinem
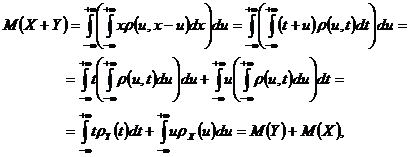
deci ![]() .
.
Se arata in mod analog ca relatia de la punctul precedent.
Definitia 11. Numim dispersia (variatia) variabilei aleatoare X, caracteristica numerica
![]()
iar caracteristica numerica ![]() se numeste
abatereaa medie patratica (abatere standard).
se numeste
abatereaa medie patratica (abatere standard).
Prpozitia 12. Dispersia satisface urmatoarele proprietati
(1) ![]()
(2) ![]()
(3) daca variabilele aleatoare X si Y sunt independente, atunci
![]()
Demonstratie.
Avand in vedere proprietati ale valorii medii, putem scrie succesiv
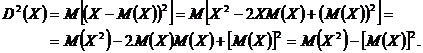
Se procedeaza analog si se obtine
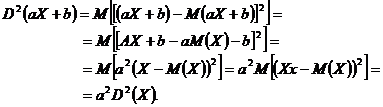
Deoarece vriabilele aleatoare X si Y sunt independente, rezulta succesiv
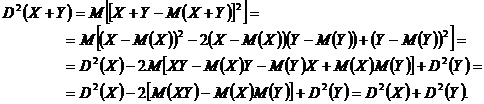
Observatia 13. Deoarece ![]() folosind (1), avem
ca
folosind (1), avem
ca ![]() , iar din (2), considerand
, iar din (2), considerand ![]() se obtine ca
dispersia unei constante este zero.
se obtine ca
dispersia unei constante este zero.
Exemplul 1 Fie variabila aleatoare X ce urmeaza legea binomiala, adica are distributia
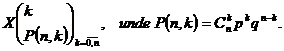
Pentru a calcula dispersia variabilei X, folosim
formula ![]() . Se stie ca
. Se stie ca ![]() Ramane sa
calculam valoarea medie
Ramane sa
calculam valoarea medie ![]() Pentru aceasta avem
succesiv
Pentru aceasta avem
succesiv
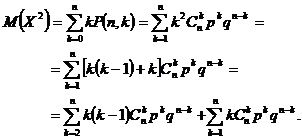
Ultima suma este chiar ![]() iar cealalta
suma se calculeaza aplicand de doua ori formula de
recurenta pentru numarul de combinari, anume
iar cealalta
suma se calculeaza aplicand de doua ori formula de
recurenta pentru numarul de combinari, anume
![]()
Astfel, se poate scrie
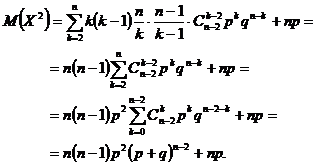
Deoarece ![]() rezulta ca
rezulta ca ![]() si drept urmare
avem
si drept urmare
avem
![]() ,
,
deci ![]()
Exemplul 15 Daca variabila alatoare X urmeaza legea normala ![]() , atunci are densitatea de porbabilitate
, atunci are densitatea de porbabilitate
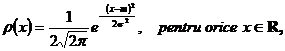
iar valoarea medie este ![]()
Folosind definitia dispersiei, se scrie
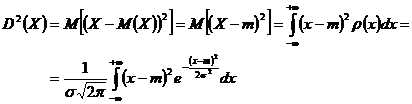
Pentru calculul integralei facem schimbarea de variabila
![]() si vom obtine
si vom obtine
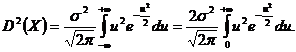
Pentru ultima egalitate am avut in vedere ca
functia ce se integreaza este functie para, iar intervalul
de integrare este simetric fata de origine. Mai efectuam
schimbarea de variabila ![]() ceea ce conduce la
ceea ce conduce la
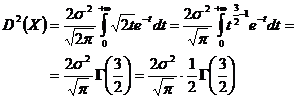
Dar se stie ca ![]() arfel ca
arfel ca ![]()
Definitia 16. Numim moment (initial) de ordin k pentru variabila aleatoare X, caracteristica numerica ![]()
Observatia 17 Pentru ![]() avem ca
avem ca ![]() adica momentul
initial de ordinul intai este chiar vloarea medie. De asemenea, avem
ca
adica momentul
initial de ordinul intai este chiar vloarea medie. De asemenea, avem
ca ![]()
Definitia 18 Numim moment centrat de ordinul k al varaibialei aleatoare X, caracteristica numerica ![]()
Observatia 19. Pentru ![]() avem ca
avem ca
![]()
iar pentru ![]() se obtine
se obtine
![]()
Proprietatea 20. Intre momentele centrate si momentele initiale exista urmatoarea relatie
![]()
Demonstratie. Folosind formula binomului lui Newton si avand in vedere proprietatile valorii medii, se poate scrie
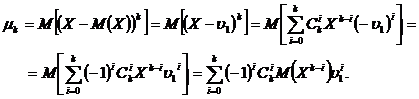
Inlocuindu-se 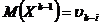 si retinand
extremitatile acestui sir de egalitati se obtine relatia
enuntata.
si retinand
extremitatile acestui sir de egalitati se obtine relatia
enuntata.
Observatia 21. In statistica matematica se utilizeaza de regula momente centrate pana la ordinul patru, pentru care avem:
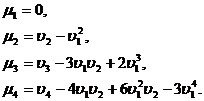
Exemplul 22. Vrem
sa calculam momentele centrate ale variabilei aleatoare X ce urmeaza legea normala ![]() . Se stie ca variabila aleatoare X are media
. Se stie ca variabila aleatoare X are media ![]() si are densitatea
de probabilitate
si are densitatea
de probabilitate
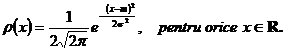
Momentul centrat de ordinul k se calculeaza cu formula
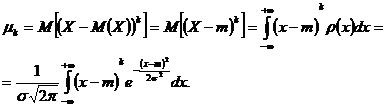
Pentru calculul acestei integrale, facem schimbarea de variabila
data prin relatia ![]() ,
, ![]() .Astfel obtinem ca:
.Astfel obtinem ca:
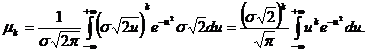
Se observa ca pentru k
impar, adica k = 2r-1, functia care se
integreaza este functie impara, iar intervalul de integrare este
simetric fata de origine, drept urmare integrala este zero, deci ![]()
Pentru k=2r, functia care se integreaza este functie para, deci
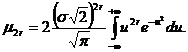
In aceasta integrala se
face schimbarea de variabila ![]() .Astfel se obtine
.Astfel se obtine
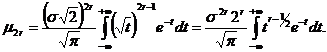
Cunoastem ca functia gamma a lui Euler este definita prin
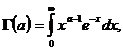 pentru orice a > 0.
pentru orice a > 0.
si ca verifica
relatia de recurenta ![]() iar pe de alta parte
iar pe de alta parte ![]() Folosind aceste rezultate putem scrie succesiv
Folosind aceste rezultate putem scrie succesiv
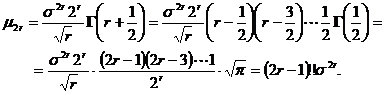
In concluzie
![]()
Definitia 23. Numim
moment (initial) de ordinul ![]() al vectorului aleator
al vectorului aleator ![]() , caracteristica numerica
, caracteristica numerica ![]() si de asemenea
numim moment (centrat) de ordinul
si de asemenea
numim moment (centrat) de ordinul ![]() al vectorului aleator
al vectorului aleator ![]() , caracteristica numerica
, caracteristica numerica
![]()
Observatia 2 Prin particularizari ale lui r si s avem:
![]() si
si ![]() respectiv
respectiv
![]() si
si
![]()
Definitia 25. Numim corelatia sau covarianta dintre variabilele aleatoare X si Y, caracteristica numerica
![]()
Observatia 26. Daca se aplica proprietatile valorii medii, avem ca
![]()
adica ![]()
Observatia 27. Daca variabilele aleatoare X si Y sunt independente, atunci
![]() deci
deci ![]()
Definitia 28. Numim coeficient de corelatie dintre variabilele aleatoare X si Y, caracteristica numerica
![]()
Observatia 29. Din Observatia 27 avem ca daca
varibilele aleatoare X si Y sunt independente, atunci ![]()
De
asemenea, daca ![]() vom spune ca
variabilele aleatoare sunt necorelate, ceea ce nu este echivalent cu
independenta variabileleor aleatoare.
vom spune ca
variabilele aleatoare sunt necorelate, ceea ce nu este echivalent cu
independenta variabileleor aleatoare.
Propozitia 30 Coeficientul de corelatie satisface urmatoarele proprietati:
(1) ![]() sau
sau ![]()
(2) ![]() daca si
numai daca
daca si
numai daca ![]()
Demonstartie.
S considera varibila aleatoare definita prin
![]()
Astfel avem ca ![]() pentru orice
pentru orice ![]() .
.
Pe de alta parte putem scrie
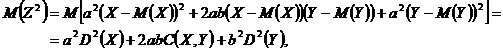
pentru orice ![]() .
.
Rezulta ca discriminantul ![]() Prin urmare, se
obtine ca
Prin urmare, se
obtine ca ![]() sau
sau
![]() adica
adica 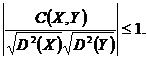
Astfel s-a ajuns la ![]() sau
sau ![]()
Consideram variabile aleatoare normate reduse
![]()
pentru care avem ![]() si
si
![]()
Pe
de alta parte, considerand variabilele aleatoare ![]() dupa cum
dupa cum ![]() avem ca
avem ca
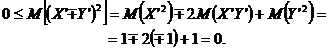
Din acest sir de relatii se obtine
ca ![]() prin urmare
prin urmare ![]() de unde rezulta
ca
de unde rezulta
ca ![]() , unde constantele
, unde constantele ![]() pot fi determinate.
pot fi determinate.
Invers,
daca ![]() ,
, ![]() , atunci
, atunci
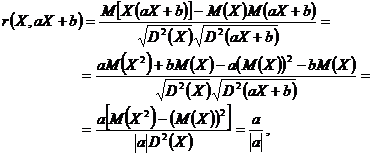
de unde ![]() , dupa cum
, dupa cum ![]() , respectiv
, respectiv ![]()
Exemplul 31. Fie variabilele aleatoare X si Y, care verifica relatia ![]() iar variabila aleatoare X
are distributia
iar variabila aleatoare X
are distributia
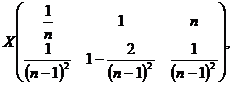
unde ![]()
Deoarece
![]() adica
adica ![]() avem distributia variabilei Y data prin
avem distributia variabilei Y data prin
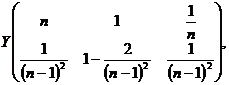
Vom calcula coeficientul de corela'ie dintre X si Y. Pentru aceasta avem
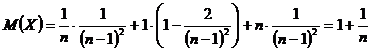
si de asemenea, ![]()
Pentru a calcula dispersiile X si Y, calculam
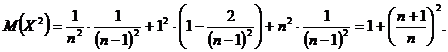
In mod analog, avem ca ![]()
Prin urmare, obtinem ca
![]()
si in mod analog ![]()
Mai
avem ca ![]() .
.
Astfel, in final, se ajunge la
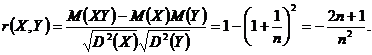
Definitia 32. Numim mediana unei variabile aleatoare X, caracteristica numerica m, care satisface conditia
![]()
Observatia 33. Daca
F este functia de repartitie a variabilei aleatoare X, atunci ![]() si
si ![]() Prin urmare,
conditia din definitia medianei se poate pune sub forma
echivalenta
Prin urmare,
conditia din definitia medianei se poate pune sub forma
echivalenta ![]() .
.
Ca
o consecinta a acestei scrieri, avem ca daca F este continua, atunci mediana m este data de ecuatia ![]()
Observatia 3 Madiana unei variabile aleatoare poate avea o
infinitate de valori, in cazul in care dreapta de ecuatie ![]() si curba de
ecuatie
si curba de
ecuatie ![]() au in comun un segment,
deci graficele acestora coincid pe un interval, sa zicem
au in comun un segment,
deci graficele acestora coincid pe un interval, sa zicem ![]() . In acest caz, de regula, se ia
. In acest caz, de regula, se ia ![]()
Definitia 35. Numim valoare modala sau modul variabilei aleatoare X, orice punct de maxim local al distributiei lui X (in cazul discret), respectiv al densitatii de probabilitate (in cazul continuu).
Observatia 36. Dcaa exista o singura vloare modala pentru variabila aleatoare X, vom spune ca aceasta este uninominala, iar daca exista doua sau mai multe valori modale o numim bimodala, respectiv plurimodala.
Definitia 37 Numim asimetria variabilei aleatoare X, caracteristica numerica
definita prin ![]()
Observatia 38. Daca variabila aleatoare X urmeaza legea normala ![]() , atunci
, atunci ![]() De asemenea, pentru o
lege unimodala, daca
De asemenea, pentru o
lege unimodala, daca ![]() , atunci ordonata
maxima a disributiei corespunde unei abcise mai mari decat valoarea
medie, iar daca
, atunci ordonata
maxima a disributiei corespunde unei abcise mai mari decat valoarea
medie, iar daca ![]() fenomenul este invers.
fenomenul este invers.
Definitia 39. Numim exces al variabilei aleatoare X, caracteristica numerica
data prin ![]()
Observatia 40. Daca
variabila aleatoare X urmeaza
legea normala ![]() , atunci
, atunci ![]() De aseaenea, pentru o lege unimodala, daca
De aseaenea, pentru o lege unimodala, daca ![]() atunci graficul
distributiei are un aspect turtit, in raport cu legea normala,
si se numeste platicurtica, iar daca
atunci graficul
distributiei are un aspect turtit, in raport cu legea normala,
si se numeste platicurtica, iar daca ![]() , atunci are un aspect ingustat (ascutit), in raport cu
legea normala, caz in care se numeste leptocurtica.
, atunci are un aspect ingustat (ascutit), in raport cu
legea normala, caz in care se numeste leptocurtica.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3014
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved