| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Derivabilitate (Gateaux) si diferentiabilitate (Frchet) de ordinul I.
Derivate (ordinare, directionale, partiale) si diferentiale (gradienti, jacobiene)
I
I.1) Sa se studieze derivabilitatea ( dupa caz - ordinara, directionala, Gateaux sau partiala a ) urmatoarelor functii, in punctele ori pe multimile si - unde este cazul - pe directiile indicate:
a) ![]() ,
, 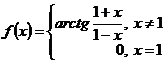 , in
, in ![]() ;
;
b) ![]() ,
, ![]() , pe
, pe ![]() ;
;
c) ![]() ,
, ![]() , pe R ;
, pe R ;
d) ![]() ,
, 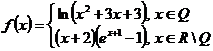 , in
, in ![]() ;
;
e)
![]() ,
, ![]() , in
, in ![]() , pe directia vectorului
, pe directia vectorului ![]() ;
;
f) ![]() ,
, ![]() , in
, in ![]() ;
;
g) ![]() ,
, ![]() , intr-un punct din
, intr-un punct din ![]() ,
,
pe directia v a intersectiei planelor ![]() si
si ![]() ;
;
h)![]() ,
, ![]() in punctul
in punctul ![]() , pe directia
, pe directia
v
a dreptei ce trece prin punctele ![]() si
si ![]() ;
;
i) ![]() ,
, 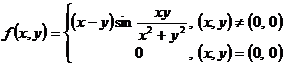 , in
, in ![]() ;
;
j) ![]() ,
, ![]() , in
, in ![]() , unde
, unde 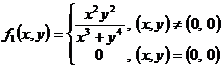 si
si 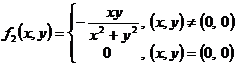 .
.
I.2) Sa se analizeze diferentiabilitatea ( Frchet ) in origine a fiecareia din urmatoarele functii:
a) ![]() ,
, ![]() ;
;
b) ![]() ,
, ![]() ,
, 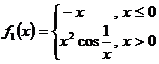 ,
, ![]() ;
;
c) ![]() ,
, 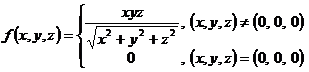 ;
;
d) ![]() ,
, ![]() ,
,
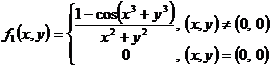 ,
, 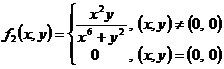 .
.
I.3) Sa se investigheze derivabilitatea functiei limita a sirului sau, dupa caz, suma a seriei de
functii de mai jos:
a) ![]() , unde
, unde ![]() ;
;
b) ![]() , unde
, unde 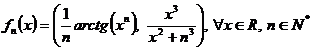 ;
;
c) ![]() , unde
, unde ![]() ;
;
d) ![]() , unde
, unde 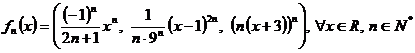 ;
;
e) ![]() , unde
, unde ![]() ;
;
f) ![]() , unde
, unde 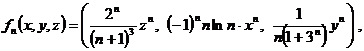
![]() .
.
II
II.1) Fie ![]() ,
, ![]() .
.
a) Sa se studieze derivabilitatea Gateaux si diferentiabilitatea Frchet a lui f pe Ker f ;
b)
Sa se arate ca jacobiana
functiei f exista si
este singulara in orice punct din ![]() .
.
II.2) Fie 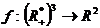 ,
, ![]() , unde
, unde ![]() si
si ![]() .Sa
se calculeze:
.Sa
se calculeze:
a) ![]() si
si ![]() ;
;
b) ![]() in punctul
in punctul ![]() ;
;
c) ![]() si
si ![]() ;
;
d) ![]() intr-un punct curent
intr-un punct curent ![]() .
.
II.3) Sa se arate ca functiile de mai jos, derivabile pe multimea lor de definitie, satisfac relatiile indicate:
a) ![]() ,
, ![]() ;
;
b) ![]() ,
,
![]() ;
;
c) ![]() ,
, ![]() ;
;
d) ![]() ,
,
![]() ;
;
e) ![]() ,
,
![]() ;
;
f) ![]() ,
, ![]() ,
,
![]() ;
;
g) ![]() ,
,
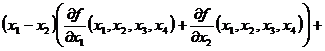
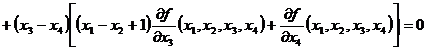 ,
,![]() .
.
II.4) Sa se determine diferentialele de ordinul intai ale urmatoarelor functii:
a) ![]() ;
;
b)
![]() ;
;
c) ![]() ,
, ![]() ;
;
d) ![]() ,
, ![]() , cu
, cu ![]() si
si ![]() .
.
II.5) Sa se verifice veridicitatea urmatoarelor afirmatii:
a)
Daca ![]() , unde
, unde ![]() , atunci
, atunci ![]() ,
, ![]() ,
, ![]() ;
;
b)
Daca ![]() , atunci
, atunci ![]() ,
, ![]() ,
, ![]() ;
;
c)
Daca ![]() , atunci
, atunci ![]() ,
, ![]() ,
, ![]() ;
;
d)
Daca ![]() , atunci
, atunci ![]() ,
, 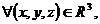
![]() .
.
F. Iacob, 01.10.2006
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2483
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved