| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Comparatia radacinilor unei ecuatii de gradul al doilea cu doua numere reale distincte
Fie ecuatia de gradul al doilea ![]() si
numerele reale a,b
(
si
numerele reale a,b
(![]() ).
Ne propunem sa stabilim seturile de conditii care
trebuie puse pentru pozitionarea corecta a radacinilor reale ale ecuatiei date
(deci conditia
).
Ne propunem sa stabilim seturile de conditii care
trebuie puse pentru pozitionarea corecta a radacinilor reale ale ecuatiei date
(deci conditia ![]() nu trebuie defel uitata).
nu trebuie defel uitata).
Am vazut ca la comparatia
radacinilor cu un singur numar real a
apareau trei cazuri distincte. Aminteam acolo ca problema se poate rezolva
relativ simplu notand y=x-a
si studiind apoi semnele ecuatiei in y care se obtine. Pentru stabilirea
pozitiei in raport cu doua numere a
si b date
(![]() ),
problema nu mai este la fel de simpla (desi se poate efectua substitutia
),
problema nu mai este la fel de simpla (desi se poate efectua substitutia
![]() ).
Apar urmatoarele 6 cazuri (cu modificari evidente cand inegalitatile sunt
stricte):
).
Apar urmatoarele 6 cazuri (cu modificari evidente cand inegalitatile sunt
stricte):
I) ![]()
II) ![]()
III) ![]()
IV) ![]()
V) ![]()
VI) ![]()
Cazul I) ![]() Setul de conditii echivalent este:
Setul de conditii echivalent este:
 (1)
(1) 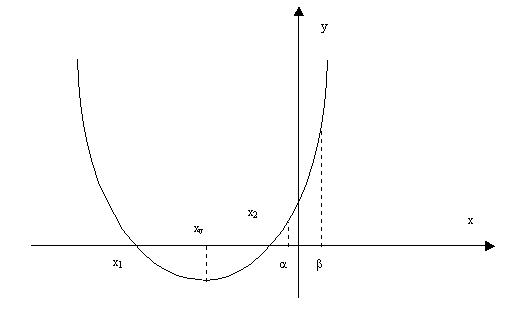
Nu mai prezentam justificarea acestor conditii; cand am comparat radacinile unei ecuatii de gradul al doilea cu un numar real a, am observat care este maniera de lucru.
Cazul II) ![]()
![]()
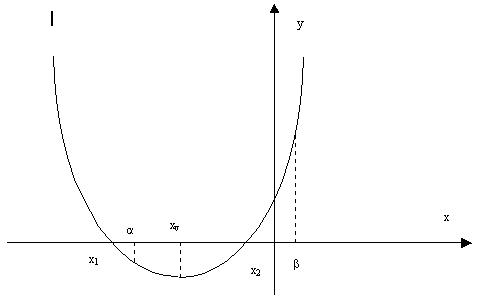
Figura 2. Pentru cazul II.
Cazul III) ![]()
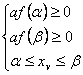 (3)
(3)
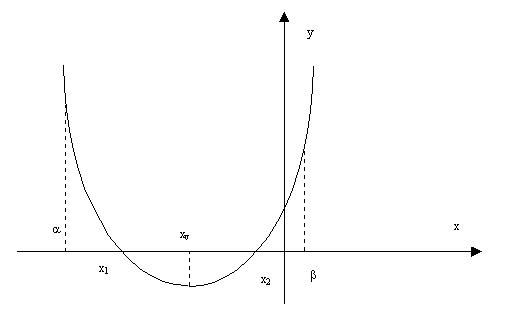
Figura 3. Pentru cazul III.
Cazul IV) ![]()
![]()
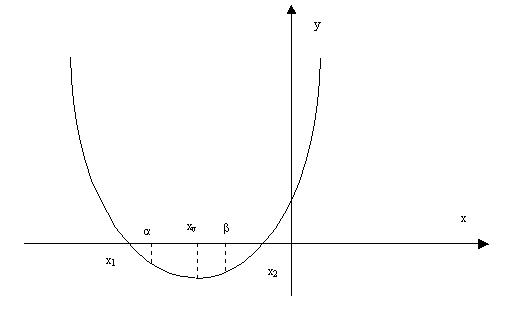
Figura 4. Pentru cazul IV.
Cazul
V) ![]()
![]() (5)
(5)
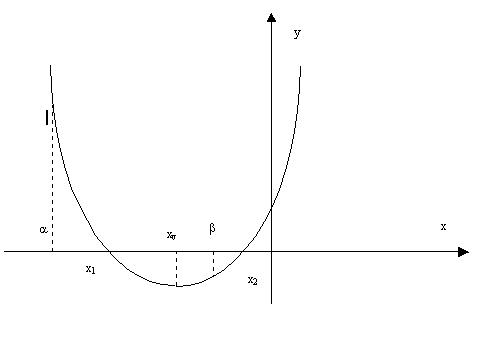
Figura 5. Pentru cazul V.
Cazul VI) ![]()

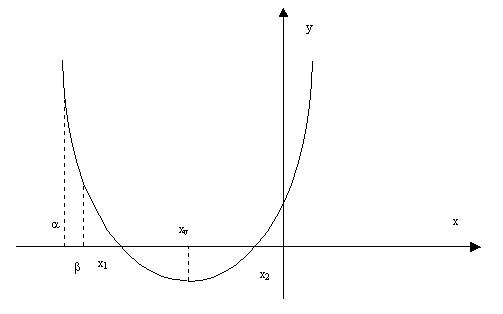
Figura 6. pentru cazul VI.
Observatie. In unele exercitii (in functie de
cerinte) este necesar si studiul cazului in care
ecuatia nu admite radacini reale (![]() ).
).
Exercitiu rezolvat (admitere,
1986) Sa se determine ![]() astfel incat functia
astfel incat functia ![]() sa pastreze semn constant pe intervalul
sa pastreze semn constant pe intervalul ![]() .
.
Solutie. Avem trei posibilitati:
a) fie functia data nu are radacini reale, deci pastreaza semn constant pe R,
deci si pe intervalul ![]()
b) fie functia
data are radacini reale, dar acestea nu apartin intervalului ![]() .
Aici vor aparea mai multe subcazuri, pe care le vom studia in mod separat.
.
Aici vor aparea mai multe subcazuri, pe care le vom studia in mod separat.
c) cazul special m=0 il vom studia separat.
Cazul a) Se pune conditia:
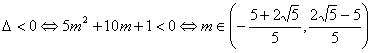
Cazul b) Punem mai intai conditia:
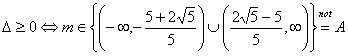
Pentru ca radacinile ![]() ale ecuatiei date sa nu se afle in intervalul
ale ecuatiei date sa nu se afle in intervalul ![]() ,
trebuie sa ne situam intr-unul din cazurile I, IV sau VI explicate in breviarul
teoretic. Calculam separat:
,
trebuie sa ne situam intr-unul din cazurile I, IV sau VI explicate in breviarul
teoretic. Calculam separat:
![]()
![]()
Punem pe rand seturile de conditii echivalente (cu inegalitati stricte):
(I): 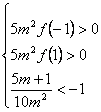
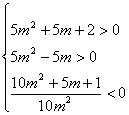
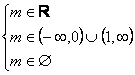
è ![]()
(IV 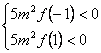
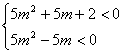
![]()
è ![]()
(VI) : 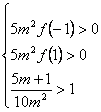
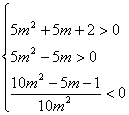
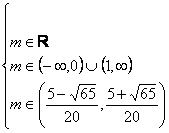 è
è
è 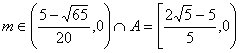
Cazul c) Daca m=0, avem f(x 1-x, care se anuleaza in x=1, deci pastreaza semn constant pe (-1,1).
Ramane sa reunim solutiile
gasite in cele trei cazuri, obtinand solutia generala 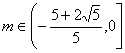
Exercitii propuse.
Sa se determine ![]() astfel incat multimea:
astfel incat multimea:
![]() sa aiba un singur
element.
sa aiba un singur
element.
Sa se determine ![]() astfel
incat multimea:
astfel
incat multimea:
![]() sa aiba doua
elemente.
sa aiba doua
elemente.
Sa se determine ![]() astfel
incat:
astfel
incat:
![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1747
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved