| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Spatii euclidiene
Definitie Fie V spatiu vectorial peste corpul de scalari K. O
aplicatie ![]() , notata
, notata ![]() se numeste produs
scalar daca satisface:
se numeste produs
scalar daca satisface:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() pentru
pentru ![]()
Definitie. Un spatiu vectorial E peste corpul K pe care s-a definit un produs scalar se numeste spatiu euclidian.
Definitie. Intr-un spatiu euclidian real sau complex, doi vectori ![]() se numesc vectori
ortogonali daca produsul loc scalar este nul, deci
se numesc vectori
ortogonali daca produsul loc scalar este nul, deci ![]()
Definitie. Fie E spatiu euclidian. Un
sistem ![]() se numeste sistem ortogonal de vectori daca
fiecare vector
se numeste sistem ortogonal de vectori daca
fiecare vector ![]() este ortogonal pe toti ceilalti vectori. Deci
este ortogonal pe toti ceilalti vectori. Deci ![]() pentru orice
pentru orice ![]() ,
, ![]() .
.
Se pleaca de la o baza oarecare a spatiului E, ![]() si se construiesc vectorii:
si se construiesc vectorii:
|
|
|
|
|
|
|
|
Scalarii ![]() se vor determina punand conditia ca oricare
doi vectori din
se vor determina punand conditia ca oricare
doi vectori din ![]() sa fie ortogonali, obtinand
sa fie ortogonali, obtinand
![]()
si prin recurenta
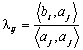
Procedeul descris mai sus poarta numele de procedeul lui Gramm - Schmidt.
Exemplu. Sa se construiasca o
baza ortogonala a spatiului euclidian ![]()
Solutie: Fie vectorii 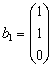
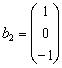 si
si 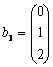 . Matricea A formata cu acesti trei vectori avand
. Matricea A formata cu acesti trei vectori avand ![]() inplica faptul ca acesti vectori formeaza o
baza a spatiului
inplica faptul ca acesti vectori formeaza o
baza a spatiului ![]() Se construiesc vectorii:
Se construiesc vectorii:
|
|
|
|
|
|
Vectorii ![]() formeaza o baza ortogonala a spatiului
formeaza o baza ortogonala a spatiului ![]() deoarece sunt trei vectori liniar independenti
si ortogonali doi cate doi.
deoarece sunt trei vectori liniar independenti
si ortogonali doi cate doi.
Definitie. Fie V spatiu vectorial peste
corpul K. O functie ![]() ,
notata
,
notata ![]() se numeste norma vectorului x,
se numeste norma vectorului x, ![]() daca verifica:
daca verifica:
![]()
![]()
![]()
Norma unui vector pe un spatiu euclidian se poate defini in mai multe feluri. Noi vom folosi norma definita cu ajutorul produsului scalar:
![]()
Definitie. Un spatiu vectorial pe care s-a definit o norma se va numi spatiu vectorial normat.
Propozitie: In orice spatiu vectorial normat exista o baza ortonormata adica o baza ortogonala in care norma fiecarui vector este egala cu unitatea.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1727
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved