| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
De multe ori este util sa aproximam o curba in jurul unui punct al sau printr-un arc de cerc care are aceeasi curbura ca si curba in punctul respectiv.
Fie C o curba parametrizata plana si urma sa.
Definitie. Se numeste cerc de curbura (osculator) al curbei C in punctul M I , cercul care:
este tangent in punctul M la curba C;
are convexitatea in jurul punctului M indreptata in aceeasi parte ca si urma curbei;
are aceeasi curba ca si curba in punctul M.
Centru cercului de curbura se numeste centru de curbura.
Din definitie rezulta ca centrul de curbura se afla pe normala la curba in punctul considerat de aceeasi parte cu convexitatea. Raza cercului de curbura este raza de curbura R a curbei in punctul respectiv. Asadar
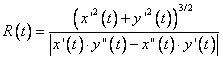 (8.1)
(8.1)
in cazul curbelor definite parametric de ecuatiile x = x(t), y = y(t), t I I si
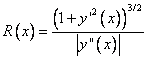 (8.2)
(8.2)
pentru curbele definite explicit de ecuatia y = y(x), x I I
Cand curba este concava, ca in fig. 8.1, y'(x) < 0, deci |y'(x)| = - y'(x).
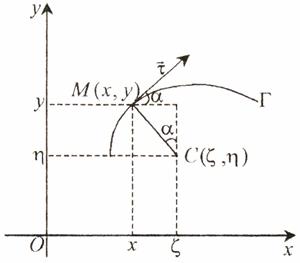
Fig. 8.1.
In consecinta, pentru R vom folosi formula
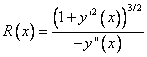 , (8.3)
, (8.3)
formula corespunzatoare curbelor definite parametric fiind
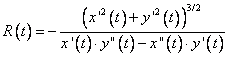
In continuare vom stabili formulele pentru coordonatele centrului de curbura. Pentru aceasta, fie M(x(t), y(t)) un punct pe curba si C(ξ(t), (t)) centrul de curbura (fig. 8.1).
Proiectand ortogonal segmentul MC pe axele de coordonate, gasim
![]() ,
, ![]() (8.4)
(8.4)
Pe de alta
parte, daca ![]() este versorul tangentei,
atunci
este versorul tangentei,
atunci ![]() . In consecinta
. In consecinta
![]()
Inlocuind in formulele (8.4), obtinem coordonatele centrului de curbura:
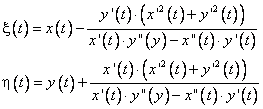 (8.5)
(8.5)
Se poate constata usor ca formulele (8.5) raman valabile si in cazul in care curba este convexa.
Observatie. Cercul de curbura (osculator) intr-un punct M al unei curbe se mai poate defini ca pozitie limita a unui cerc care trece prin trei puncte ale curbei, apropiate de M, cand acestea tind catre punctul M.
Probleme rezolvate.
1) Sa se determine coordonatele centrului de curbura intr-un punct oarecare al cicloidei de ecuatii parametrice
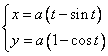
![]()
Solutie. Calculand, obtinem ![]()
![]() . Folosind (8.5),
rezulta
. Folosind (8.5),
rezulta ![]()
![]()
2) Fie elipsa x = acost, y = bsint, t I p]. Sa se scrie ecuatia cercului osculator in punctul A(0, b).
Solutie.
In acest caz ![]() .
Coordonatele centrului osculator sunt
.
Coordonatele centrului osculator sunt ![]()
![]() , iar
raza de curbura este
, iar
raza de curbura este ![]() In
consecinta, ecuatia cercului osculator in punctul A este
In
consecinta, ecuatia cercului osculator in punctul A este
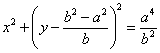
Fie ![]() , F I C1(D). Ecuatia
, F I C1(D). Ecuatia
F(x, y, t) = 0 (8.6)
defineste pentru orice t I ![]() fixat o curba plana Ct. Multimea curbelor Ct se numeste familie
de curbe plane (cu un parametru), iar ecuatia (8.6) se numeste ecuatia familiei de curbe.
fixat o curba plana Ct. Multimea curbelor Ct se numeste familie
de curbe plane (cu un parametru), iar ecuatia (8.6) se numeste ecuatia familiei de curbe.
Definitie.
O curba plana C se numeste infasuratoarea familiei t, daca, pentru orice
M I C, exista o curba unica din
familia t care este tangenta in M la curba C si orice curba din familie nu are un arc comun cu C (fig. 8.2).
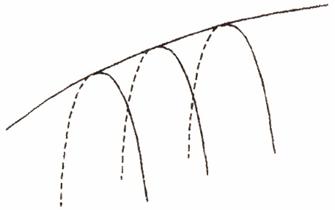
Fig. 8.2.
Sa presupunem acum ca infasuratoarea exista si ca are un singur punct de contact cu fiecare curba din familie. In consecinta, cooronatele acestui punct de contact se exprima in mod unic din ecuatia unei curbe Ct, adica prin valoarea parametrului t:
x = x(t), y = y(t) (8.7)
Deoarece infasuratoarea este formata din puncte de contact, aceste ecuatii dau si reprezentarea parametrica a infasuratoarei. Punctul (x(t), y(y)) verificand (8.6), rezulta ca
F(x(t), y(t), t) = 0 (8.8)
Derivand in raport cu t, gasim:
![]() (8.9)
(8.9)
Coeficientul unghiular al tangentei la curba (8.6) este
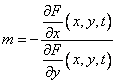
iar curba (8.7) este
![]()
Conditia m = m1 conduce la relatia
![]()
Tinand seama de (8.9), rezulta
![]() (8.10)
(8.10)
Identitatile (8.7) si (8.10) arata ca x(t) si y(t) trebuie sa verifice sistemul de ecuatii
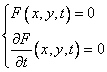 (8.11)
(8.11)
Asadar, daca infasuratoarea exista, reprezentarea ei parametrica (8.7) se obtine rezolvand sistemul (8.11) in raport cu x si y.
Problema rezolvata. Sa se gaseasca ecuatia infasuratoarei familiei de cercuri
(x - t)2 + y2 = r2, r = const.
Solutie. Derivand in raport cu t gasim x = t. Eliminand in
ecuatia familiei, obtinem
y2 - r2 = 0, adica y = t. Asadar, infasuratoarea este formata din doua drepte paralele cu
axa Ox.
Fie curba de ecuatii
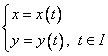 (8.12)
(8.12)
Definitie. Se numeste evoluta unei curbe plane infasuratoarea familiei normalelor la curba data.
Reamintim ca ecuatia normalei la o curba plana este
![]() (8.13)
(8.13)
Ecuatia 8.13 este ecuatia unei familii de curbe plane, parametrul fiind t. Derivand (8.13) in raport cu t obtinem
![]() (8.14)
(8.14)
Din sistemul (8.13), (8.14) rezulta
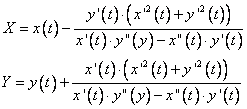 (8.15)
(8.15)
Aceste ecuatii pot fi considerate ca ecuatii parametrice ale evolutei.
Comparand cu (8.7), rezulta ca evoluta este locul geometric al centrelor de curbura ale unei curbe date.
Problema rezolvata. Sa se gaseasca evoluta elipsei x = acost, y = bsint, t I p
Solutie. Din (8.15) gasim
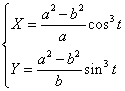
Aceasta este reprezentarea parametrica a evolutei elipsei. Eliminand parametrul t, gasim ecuatia acestei evolute sub forma implicita:
![]()
Aceasta curba aminteste de astroida (fig. 8.3)
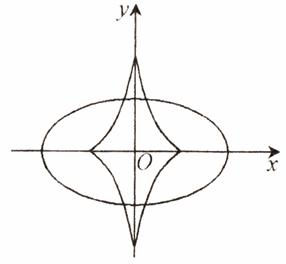
Fig. 8.3
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2830
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved