| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Derivate partiale de ordin superior
Fie ![]() o functie reala definita pe
o functie reala definita pe ![]() . Se
presupune ca functiile
. Se
presupune ca functiile ![]() si
si ![]() sunt definite pe
sunt definite pe ![]() si ca au derivate partiale pe
si ca au derivate partiale pe ![]() . Atunci
exista urmatoarele derivate partiale de ordinul II:
. Atunci
exista urmatoarele derivate partiale de ordinul II:
![]()
![]()
![]()
![]()
Functiile ![]() ,
, ![]() se numesc derivate mixte de ordinul II.
se numesc derivate mixte de ordinul II.
O functie de ![]() variabile
variabile ![]() poate avea
poate avea ![]() derivate partiale de ordinul doi,
derivate partiale de ordinul doi, ![]() ,
, ![]() .
.
Enuntam urmatoarele teoreme:
Teorema 2 (Criteriul lui Young). Daca functia ![]() are derivate
partiale de ordinul intai
are derivate
partiale de ordinul intai ![]() si
si ![]() intr-o vecinatate
intr-o vecinatate ![]() a lui
a lui ![]() si daca
si daca ![]() si
si ![]() sunt
diferentiabile in
sunt
diferentiabile in ![]() , atunci derivatele partiale mixte de ordinul doi in
, atunci derivatele partiale mixte de ordinul doi in ![]() exista si sunt
egale in acest punct,
exista si sunt
egale in acest punct, ![]()
Diferentiala
de ordinul ![]() in punctul
in punctul ![]() se defineste prin egalitatea:
se defineste prin egalitatea:
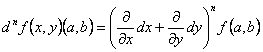
unde
exponentul ![]() inseamna ca se dezvolta suma din paranteza
dupa regula binomului lui Newton si apoi se inmulteste formal cu
inseamna ca se dezvolta suma din paranteza
dupa regula binomului lui Newton si apoi se inmulteste formal cu ![]() .
.
Diferentiala de ordinul ![]() pentru o functie de
pentru o functie de ![]() variabile va fi:
variabile va fi:
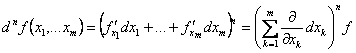
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3147
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved