TESTE TIP C
Sa
se calculeze ultima cifra a numarului E1999 unde
E = 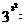
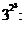
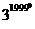 - (33 25)6 : (317
230) + 3 (5 + 2 3 - 2430 : 405).
- (33 25)6 : (317
230) + 3 (5 + 2 3 - 2430 : 405).
Bisectoarea
unghiului 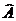 al triunghiului ABC intersecteaza (BC) in D. Fie
al triunghiului ABC intersecteaza (BC) in D. Fie 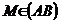 si
si 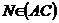 astfel incat
astfel incat 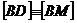 si
si 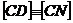 . Daca
. Daca 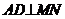 , demonstrati ca :
, demonstrati ca :
i)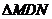 isoscel ;
isoscel ;
ii)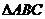 isoscel.
isoscel.
Calculati
media geometrica a numerelor 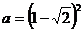 si
si 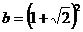 .
.
Sa
se rezolve si sa se discute ecuatia:
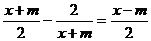 unde
unde 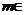 R.
R.
TESTUL C 2
Aflati cel mai mic numar natural care
impartit la 7 sa dea restul 6 si impartit la 5 sa dea restul 4.
Se da 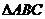
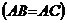 ,
, 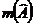 = 20.Pe latura AC se considera punctele M si E astfel incat
= 20.Pe latura AC se considera punctele M si E astfel incat
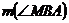 = 20,
= 20, 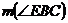 = 20, iar pe latura AB se ia punctul N astfel incat
= 20, iar pe latura AB se ia punctul N astfel incat 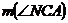 =
=
= 30. Aratati ca 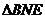 este
echilateral ;
este
echilateral ;
Calculati valoarea expresiei
E =
(tg 1 - 1) (tg 2 - 1) (tg 3 - 1) (tg
89 - 1).
O prisma dreapta are bazele romburi cu
diagonalele de 6 cm si 8 cm. Inaltimea prismei este de 5 cm.
Sa se afle aria totala a prismei.
Se dau multimile :
A =
,
B =
,
C
Calculati :
a)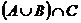 ; b) card
; b) card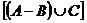
Fie [AD] bisectoarea unghiului 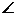 BAC al triunghiului
BAC al triunghiului
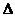 ABC si E mijlocul laturii [AC]. Stiind ca
ABC si E mijlocul laturii [AC]. Stiind ca 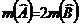 si DE║ AB, sa se calculeze masurile unghiurilor triunghiului.
si DE║ AB, sa se calculeze masurile unghiurilor triunghiului.
Fie N = 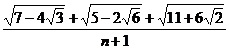 . Sa se afle numarul intreg n
. Sa se afle numarul intreg n Z astfel incat N sa
Z astfel incat N sa
fie intreg.
Simplificati expresia : 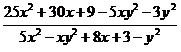 .
.
De ziua de nastere a lui Nicusor, 6.XII.1997,
bunicul i-a spus : Tatal tau, eu si tu avem astazi impreuna
115 ani. Cati ani avem fiecare, daca fiul meu este nascut in
anul MCMLIX, iar eu sunt de 6 ori mai in varsta ca tine ?
Numerele rationale 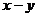 ,
, 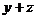 si
si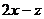 sunt invers proportionale cu 0,(3) ; 0,25 si
0,2.
sunt invers proportionale cu 0,(3) ; 0,25 si
0,2.
a)
Cu ce numere sunt direct proportionale x,
y si z.
b)
Daca 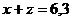 calculati x, y
si z.
calculati x, y
si z.
Sa se rezolve ecuatia:
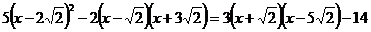 , unde x
, unde x R.
R.
Aratati ca un paralelipiped dreptunghic
pentru care patratul diagonalei este egal cu jumatate din aria sa
totala devine cub si reciproc.
Sa se afle ultima cifra a numarului : N = 31992 + 41994
+ 51996 + 61998 + 72000
Se da triunghiul isoscel  ABC cu [AB]
ABC cu [AB] [AC]. Fie [AD] mediana corespunzatoare laturii
[BC], [AE bisectoarea unghiului
[AC]. Fie [AD] mediana corespunzatoare laturii
[BC], [AE bisectoarea unghiului 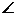 BAD, E
BAD, E (BC), iar AF
este bisectoarea unghiului
(BC), iar AF
este bisectoarea unghiului 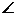 DAC, F
DAC, F (BC).
(BC).
a) Demonstrati ca 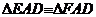 .
.
b) Demonstrati ca daca intr-un
triunghi isoscel, masura unui unghi este egala cu media
aritmetica a celorlalte doua
unghiuri, atunci triunghiul este echilateral.
Aflati (x ;y) R x R pentru care avem:
R x R pentru care avem:
59x + 41y = 59 si 41x + 59y = 41.
Un cub are diagonala egala cu 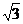 m. Aflati
capacitatea in litri a acestui cub.
m. Aflati
capacitatea in litri a acestui cub.
Aratati ca produsul a cinci numere naturale
consecutive se divide cu 120.
Doi muncitori termina o lucrare, lucrand impreuna,
in 4 zile. Primul muncitor lucrand singur termina lucrarea in 6 zile. In
cate zile termina lucrarea al doilea muncitor lucrand singur ?
Calculati:
a) 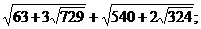
b)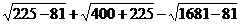 ;
;
c) 5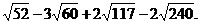
O piramida patrulatera regulata are latura
bazei egala cu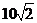 cm. Cat de mare trebuie sa fie
cm. Cat de mare trebuie sa fie
unghiul format de o muchie
laterala cu planul bazei, ca volumul piramidei sa fie egal cu
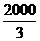 cm3?
cm3?
- Sa se arate ca pentru orice
n
 N*,
N*,
E = 52n 72n + 1
112n - 25n 72n 112n+1 - 52n+1
49n 121n se divide cu 5005.
- Pretul unui produs creste cu 25%.Cu cat la suta trebuie sa scada
noul pret pentru a obtine pretul initial al
produsului ?
- Aratati ca mijloacele laturilor unui romb formeaza
un dreptunghi.
- a) Sa se simplifice expresia
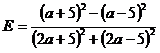 si sa se arate ca
si sa se arate ca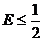 pentru orice numar real a.
pentru orice numar real a.
b) Fie a,b,c
si p numere reale astfel
incat a + b + c = 6p.Aratati ca 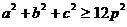 .
.
Aflati
elementele multimii: A = .
Daca
M1 este mijlocul
segmentului [AB], M2 este mijlocul segmentului
[AM1], . , M10 este mijlocul segmentului
[AM9] si daca AB = 211 3 cm, aflati
lungimea segmentului [AM10].
Calculati: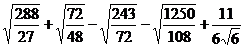 .
.
Se
da un triunghi ABC cu aria de 96
cm2.Laturile sale sunt proportionale cu numerele 3, 4, si
5. Se cere:
a)
Aflati laturile triunghiului ;
b) Calculati
razele cercurilor inscris si circumscris triunghiului ABC ;
c)
Determinati volumul piramidei VABC
stiind ca 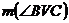 = 120 si VA = VB
= VC.
= 120 si VA = VB
= VC.
TESTUL C 9
- Calculati
suma:
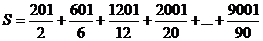 .
.
- Se dau
punctele O, A, B si M. Stiind ca O
 (AB), M este mijlocul segmentului [AB], OA = 32 cm si OM
= 14 cm, sa se afle OB.
(AB), M este mijlocul segmentului [AB], OA = 32 cm si OM
= 14 cm, sa se afle OB.
- Descompuneti
in factori ireductibili:
a) 9(x +
3)2 - 4x2; b)
625 - x4; c) 3x2 - 1; d) x4 + 3x2 + 4; e) 36x2
+60xy + 25y2.
- Pe planul
patratului ABCD se
ridica perpendiculara DM =
6
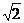 cm. Stiind ca
cm. Stiind ca 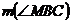 = 60, sa se afle:
= 60, sa se afle:
a) distanta de la punctul M la AC ;
b) distanta de la punctul D la MB ;
c) distanta de la punctul D la planul (MAC).
TESTUL C 10
- Aflati
numarul natural a pentru care
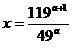
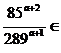 N.
N.
- Aflati
trei numere naturale stiind ca sunt direct proportionale cu
3, 5 si 7, iar produsul lor este 139755.
- Fie
triunghiul ABC si M
 (BC).Dreptele
MN si MP sunt paralele respective cu AB si AC ( N
(BC).Dreptele
MN si MP sunt paralele respective cu AB si AC ( N (AC), P
(AC), P (AB)).Demonstrati
ca
(AB)).Demonstrati
ca 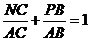 .
.
- Fie
expresiile
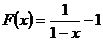 si
si 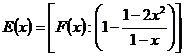
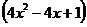 , unde x
, unde x R-.
R-.
a) Calculati F(2) F(-1);
b) Aratati ca E(x) = 2x - 1;
c) Cate elemente are A = ;
d) Calculati E(2) + E(3) + E(4) + + E(25).
TESTUL C 11
- Se dau
numerele: a = (1 + 2 + 3 + . +
1999) ∙ 2 : 2000 si b
= (217 : 48)2000 : 8666.
Calculati 2(a + b) - 100.
- Fie
numarul: N = 1 (-1) + 2
(-1)2 + 3 (-1)3 + . + n (-1)n. Calculati N
pentru :
a) n = 2003; b) n = 2004.
- In triunghiul
ABC avem: AB = 9, BC = 15, AC = 18, D
 (AB)
astfel incat AD = 6.Paralela
prin D la BC intersecteaza AC
in E. Calculati perimetrul
triunghiului
(AB)
astfel incat AD = 6.Paralela
prin D la BC intersecteaza AC
in E. Calculati perimetrul
triunghiului 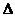 ADE.
ADE.
- Rezolvati
sistemele:
a) 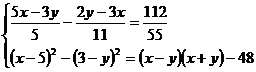 b)
b) 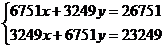
- Calculati restul
impartirii numarului N
= 1 2 3 . 1999 + 100 la numarul 99.
- Care este probabilitatea ca aruncand
doua zaruri sa obtinem doua fete in care suma
punctelor sa fie un numar prim?
- Fie ABCD un trapez in care AB║CD, AB = 42, BC = 32, CD = 14 si AD = 12.
Daca AD BC= = , calculati OC si OD.
BC= = , calculati OC si OD.
- Intr-un con circular drept, raza este
4 cm, iar generatoarea face cu planul bazei un unghi de 60.Se cere :
a) aria laterala si volumul conului;
b) distanta de la varf la planul de
sectiune paralel cu baza, pentru care aria sectiunii sa fie
egala
cu 4 cm2.
cm2.
- Un tata are cu douazeci de
ani mai mult decat fiul sau, iar peste 15 ani va avea de doua
ori varsta fiului sau. Cati ani are fiecare ?
- Doua unghiuri suplementare au
raportul masurilor lor egal cu
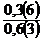 . Sa se afle masurile celor doua
unghiuri.
. Sa se afle masurile celor doua
unghiuri.
- Rezolvati in Q x Q
sistemele :
a) 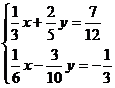 b)
b) 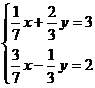
- a) O piramida patrulatera
regulata are aria laterala de 2320 m2 si aria
totala de 3920 m2.Aflati latura bazei, muchia
laterala, inaltimea, apotema si volumul piramidei.
b)
Aflati raza unei sfere pentru care aria si volumul sau sunt exprimate
prin acelasi numar
(unitatile de masura difera).
TESTUL C 14
- Calculati : a)
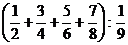 ; b)
; b) 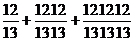 .
.
- Fie unghiurile
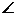 AOB,
AOB, 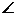 BOC,
BOC, 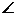 COD si
COD si 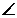 DOA in jurul unui punct O astfel incat masurile
unghiurilor
DOA in jurul unui punct O astfel incat masurile
unghiurilor 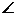 XOY,
XOY, 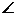 YOZ,
YOZ, 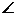 ZOT si TOX
sunt direct proportionale cu numerele 6, 7, 12 si 11, unde
semidreptele (OX, (OY, (OZ
si (OT sunt respectiv
bisectoarele unghiurilor
ZOT si TOX
sunt direct proportionale cu numerele 6, 7, 12 si 11, unde
semidreptele (OX, (OY, (OZ
si (OT sunt respectiv
bisectoarele unghiurilor 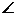 AOB,
AOB, 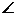 BOC,
BOC, 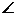 COD si
COD si 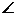 DOA. Sa se afle masurile unghiurilor
initiale daca unul dintre cele patru unghiuri este drept.
DOA. Sa se afle masurile unghiurilor
initiale daca unul dintre cele patru unghiuri este drept.
- Aflati x din:
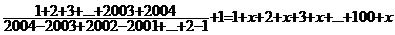 .
.
- Sa se afle raza,
inaltimea si volumul unui con circular drept pentru care
desfasurarea suprafetei laterale este un sector de disc cu
unghiul de 120 si raza de 9 cm.
- Aflati numerele naturale mai
mici decat 1000 stiind ca fiecare se imparte pe rand la 5, 6, 8,
9, 10 si 12 si se obtin respectiv resturile 4, 5, 7, 8, 9
si 11.
- Numerele a, b si c sunt direct
proportionale cu 2, 3, si 4, iar numerele b si d sunt
invers proportionale cu 2 si 9.
i)
Sa se arate ca 2a2 +
b2 + 3c2 + 10d2 este patratul unui
numar ;
ii)
Sa se afle numerele naturale a, b, c
si d stiind ca 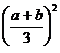
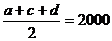 .
.
- In triunghiul
 ABC avem: M
ABC avem: M (BC), MD║AB, D
(BC), MD║AB, D (AC), ME║AC, E
(AC), ME║AC, E (AB),
(AB), 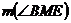 = 67 si
= 67 si 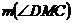 = 44.Aflati
masurile unghiurilor triunghiului
= 44.Aflati
masurile unghiurilor triunghiului 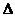 ABC.
ABC.
- Aflati aria si volumul unui
tetraedru regulat de muchie a.
TESTUL C 16
- Care dintre numerele : a = 258 si b = 339 - 919
este mai mare?
- a) Aratati ca:
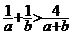 ,
, 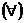 a, b > 0 si
a, b > 0 si 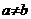 ; b)
Aratati ca :
; b)
Aratati ca :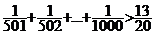 .
.
- Se da patratul ABCD. Pe latura DC se construieste triunghiul
echilateral DEC. Fie F mijlocul lui AB, EF
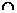 DC = , AE
DC = , AE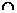 DC = . Construim MN
DC = . Construim MN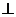 DE. Aratati ca MN = MO.
DE. Aratati ca MN = MO.
- Intr-un trunchi de con circular drept
cu R = 16 cm si r = 8 cm, se inscriu doua conuri care au ca baze
bazele trunchiului si generatoarele unuia in prelungirea
generatoarelor celuilalt. Stiind ca inaltimea
trunchiului este12 cm, aflati:
a)
aria laterala si volumul trunchiului;
b)
volumele celor doua conuri.
- Sa se determine numerele
naturale
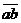 pentru care
pentru care 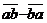 este patrat perfect.
este patrat perfect.
- Fie E(n) = (-1)n n, n
 N*.Calculati: E(1) + E(2) + + E(1999).
N*.Calculati: E(1) + E(2) + + E(1999).
- Unghiul
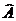 al triunghiului ABC
are masura de 50, iar unghiul
al triunghiului ABC
are masura de 50, iar unghiul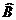 are masura de 70. Care sunt masurile
unghiurilor formate de semidreptele (AB
si (AC cu paralela prin A
la bisectoarea unghiului
are masura de 70. Care sunt masurile
unghiurilor formate de semidreptele (AB
si (AC cu paralela prin A
la bisectoarea unghiului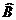 ?
?
- i) Calculati ma, mg
si mh a numerelor :
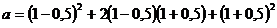 si
si
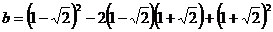 .
.
ii) De cate ori este mai mare distanta
dintre Pamant si Soare (15107 km) decat distanta
dintre
Pamant si Luna
(348103 km) ?
iii) Scrieti numarul 5 ca un produs
de doua numere care apartin multimii :
a) N ; b) Z - N ; c) Q -
Z ; d) R -Q .
TESTUL C 18
- Se da numarul A = 32n+153n+2
- 9n+153n+1.Aratati ca A se divide cu 90, oricare ar fi n
 N*.
N*.
- Daca intr-un triunghi mediana
corespunzatoare unei laturi este si bisectoarea unghiului opus
aceleiasi laturi, atunci triunghiul este isoscel.
- Se dau numerele :
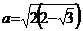 si
si 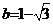 .Sa se arate ca :
.Sa se arate ca :
i)
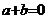 ; ii)
; ii) 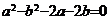 .
.
- Pe planul trapezului dreptunghic ABCD se ridica
perpendicularele CE si DF. Se stie ca : AB║CD, AD
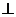 AB, AD = CD = DF = a si AB = CE = 2a. Se cere :
AB, AD = CD = DF = a si AB = CE = 2a. Se cere :
a) Aratati ca BC║(AEF);
b) Aratati ca AE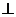 BC;
BC;
c) Aflati masura unghiului format de
dreptele BC si AF.
- Sa se gaseasca toate
numerele de forma
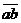 in baza 10, care au proprietatea ca
in baza 10, care au proprietatea ca 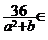 N.
N.
- lucrare trebuie sa fie
predata in 21 de zile. 12 muncitori lucreaza in 14 zile
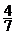 din lucrare. Cati muncitori mai trebuie
angajati pentru a respecta termenul de predare.
din lucrare. Cati muncitori mai trebuie
angajati pentru a respecta termenul de predare.
- Lungimile catetelor unui triunghi
dreptunghic ABC sunt AB = 15 cm si AC = 20 cm.
Se cer : BC, AD, BD, tg(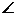 BAD) si cos(
BAD) si cos(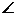 ACD).
ACD).
- i) Determinati functia
liniara al carui grafic contine punctele A(a;2) si B(-1;a);
ii)
Aflati valorile lui a R, pentru care functia este
descrescatoare ;
R, pentru care functia este
descrescatoare ;
iii)
Pentru a = 1 trasati graficul
functiei.
TESTUL C 20
- Sa se determine multimile A si B stiind ca sunt satisfacute simultan
conditiile :
a)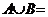 ;
;
b)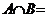 ;
;
c)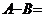 .
.
- Rezolvati ecuatia :
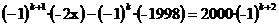 , unde k
, unde k N*.
N*.
- In triunghiul ABC se duc medianele AA'
si BB' unde A'
 (BC) si B'
(BC) si B' (AC).
(AC).
Se stie ca: AA' = 7,5
cm, BB' = 6 cm si BC = 5 cm. Sa se afle perimetrul
si inaltimea din A ale
triunghiului ABC.
- Calculati :
i)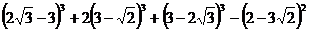 ;
;
ii) Calculati media aritmetica
si media armonica a numerelor: 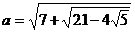 si
si
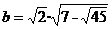 .
.
TESTUL C 21
- Aflati cel mai mic si cel mai mare
numar de forma
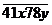 divizibil cu 15. Cate astfel de numere
exista ?
divizibil cu 15. Cate astfel de numere
exista ?
- Stiind ca x, y, z sunt direct proportionale cu 2, 3, 4 si 2x - y + 5z = 21, aflati 3x - y + 2z.
- Fie
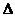 ABC
dreptunghic in A si AM mediana. Daca
ABC
dreptunghic in A si AM mediana. Daca 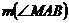 = 30,
aratati ca
= 30,
aratati ca 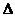 AMC este
echilateral.
AMC este
echilateral.
- Fie ABCD un dreptunghi cu AB = 10 cm si BC
= 6 cm. Prin A, B, C si D se duc de aceeasi parte a
planului (ABC), AA'║BB'║CC'║DD', unde AA' = 8 cm, BB' = 6
cm, CC' = 2 cm si DD' = 6 cm. Daca A'B'
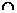 AB = si D'C'
AB = si D'C' DC = , aflati MN.
DC = , aflati MN.
TESTUL C 22
Calculati :
S1 = (3 + 5 + 7+ . +1999) - 2
- 4 - 6 - . - 1998 ;
S2 = (1 2 + 2 3 + . + 1999
2000= -12 - 22 - . - 19992.
Stiind
ca 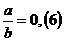 calculati x din
calculati x din 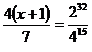
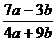 .
.
 Doua coarde ale unui cerc AB si CD se
intersecteaza in exteriorul cercului in punctul O, A
Doua coarde ale unui cerc AB si CD se
intersecteaza in exteriorul cercului in punctul O, A (OB)
si C
(OB)
si C (OD). Daca
(OD). Daca 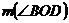 = 30, atunci :
= 30, atunci :

 i) Aflati
m(BD) si masura
unuia dintre unghiurile formate de BC
si AD, pentru care
i) Aflati
m(BD) si masura
unuia dintre unghiurile formate de BC
si AD, pentru care
m(AC) este de 20 ;
ii)
Aratati ca OA OB = OC
OD.
Aflati (x;y) R x R pentru care xy - 3x = 7 si x2y - 9x
= 175.
R x R pentru care xy - 3x = 7 si x2y - 9x
= 175.
Aflati
cel mai mare numar natural care la impartirea cu 1999 da
catul egal cu restul.
Fie AOC si
AOC si  COB doua
unghiuri adiacente suplementare, care se impart in cate trei parti
congruente prin semidreptele [OM, [ON, [OP
si [OQ (in aceasta ordine).
Se cer masurile unghiurilor
COB doua
unghiuri adiacente suplementare, care se impart in cate trei parti
congruente prin semidreptele [OM, [ON, [OP
si [OQ (in aceasta ordine).
Se cer masurile unghiurilor  NOP si
NOP si 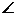 MOQ.
MOQ.
Aratati
ca :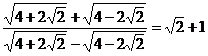 .
.
i) Daca 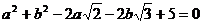 , calculati
, calculati 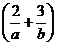
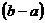 ;
;
ii)
Aflati 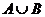 ,
, 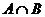 , A - B si B -A unde A = si B
, A - B si B -A unde A = si B
TESTUL C 24
- Un baiat afirma ca are tot
atatea surori cat si frati. O sora a baiatului
afirma ca are de doua ori mai multi frati decat
surori. Cati frati si cate surori sunt in acea familie?
- Sa se afle media aritmetica a tuturor
fractiilor supraunitare care au numaratorul 6.
- Calculati
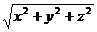 , unde x, y, z
, unde x, y, z Z si x
si y sunt numere
consecutive, iar z = xy.
Z si x
si y sunt numere
consecutive, iar z = xy.
- Pe planul patratului ABCD se ridica perpendiculara VD = AB. Fie M mijlocul
lui CV.
a)
Aratati ca BV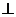 AC si VA║ (MBD);
AC si VA║ (MBD);
b)
Calculati d(D, (VBC)) stiind ca CV = 10 cm;
c)
Daca AC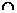 BD = , calculati DM + VO + CM;
BD = , calculati DM + VO + CM;
d)
Aflati aria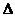 VBC.
VBC.
TESTUL C 25
- Aratati
ca numarul
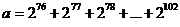 nu poate fi
patrat perfect.
nu poate fi
patrat perfect.
- Perimetrul
unui triunghi este 24 cm, iar suma oricaror doua laturi ale sale
este egala cu k, unde k
 N. Aflati natura triunghiului si cu
ajutorul instrumentelor geometrice construiti triunghiul si
liniile sale importante.
N. Aflati natura triunghiului si cu
ajutorul instrumentelor geometrice construiti triunghiul si
liniile sale importante.
- a) Sa
se stabileasca natura triunghiului ABC in care are loc relatia :
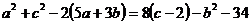 , unde a = BC, b = AC si c = AB ;
, unde a = BC, b = AC si c = AB ;
b) Sa se afle aria cercului circumscris
triunghiului ABC ;
c) Fie [CD
bisectoarea 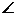 ACB, D
ACB, D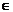 (AB). Sa se
afle aria triunghiului CAD.
(AB). Sa se
afle aria triunghiului CAD.
- Rezolvati
in R ecuatia x + 2 + 3x + 4 + 5x +6 + . + 99x
+ 100 = 50.
TESTUL C 26
- Intr-o
cutie sunt de cinci ori mai multe bile rosii decat galbene. Daca
se scot 5 bile rosii si se adauga o bila galbena
atunci in cutie sunt de 4 ori mai multe bile rosii decat galbene.
Cate bile de fiecare culoare au fost la inceput ?
- Aflati
a si b daca
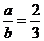 si
si 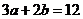 .
.
- In
triunghiul ABC,
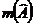 = 90, AB = 15 cm si AC = 20 cm. Pe (BC) se ia un punct P , astfel incat suma segmentelor AB si BP sa fie cu 2 cm mai mica decat suma segmentelor AC si CP. Sa se calculeze lungimea segmentului AP.
= 90, AB = 15 cm si AC = 20 cm. Pe (BC) se ia un punct P , astfel incat suma segmentelor AB si BP sa fie cu 2 cm mai mica decat suma segmentelor AC si CP. Sa se calculeze lungimea segmentului AP.
- Aflati
x, y, z
 R astfel
incat :
R astfel
incat :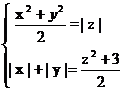
- Aflati
numarul natural x pentru care avem: a)
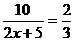 ; b)
; b) 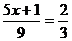 .
.
- Fie ABCD un trapez cu AB║CD, AB > CD, E
 (AD), [AE]
(AD), [AE]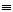 [ED], EF║AB, F
[ED], EF║AB, F (BC) si AC
(BC) si AC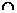 EF = . Daca EG = 3 cm si AB
= 8 cm, calculati DC, EF si GH, unde = BD
EF = . Daca EG = 3 cm si AB
= 8 cm, calculati DC, EF si GH, unde = BD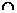 EF.
EF.
- Media
aritmetica ponderata a numerelor 6; 9 si x cu ponderile 2; 1 si 3 este
9,5. Aflati
numarul x.
- a)
Aratati ca oricare ar fi a, b, c
 R are loc egalitatea:
R are loc egalitatea:
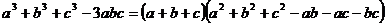 .
.
b) Aratati ca daca 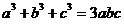 atunci paralelipipedul dreptunghic ABCDA'B'C'D' este cub, unde AB
= a, BC = b si CC' = c.
atunci paralelipipedul dreptunghic ABCDA'B'C'D' este cub, unde AB
= a, BC = b si CC' = c.
- Suma a
trei numere naturale consecutive este un numar par. Cel mai mic
dintre ele este par sau impar ?
- Aratati
ca mijloacele laturilor unui dreptunghi formeaza un romb.
- Calculati :
a)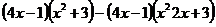 ;
;
b)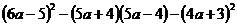 ;
;
c)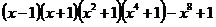 .
.
- Un con din
metal are raza de 60 cm si generatoarea de 100 cm. La o
distanta de 20 cm de varful conului se face o sectiune
paralela cu baza.
a) Aflati volumul
trunchiului de con ;
b) Din trunchi se scoate
un con care are ca baza, baza mica a trunchiului si varful in
centrul
bazei mari. Aflati
aria corpului format.
- Calculati :
a)
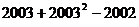 2004 ; b)
2004 ; b) 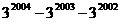 - 5
- 5 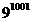 .
.
- Fie ABC un triunghi cu
inaltimea [AH], H
 (BC) si
cu mediana [AM], M
(BC) si
cu mediana [AM], M (BC). Se
prelungeste inaltimea cu un segment [HD] = [AH] si
mediana cu [ME]
(BC). Se
prelungeste inaltimea cu un segment [HD] = [AH] si
mediana cu [ME] 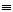 [AM]. Dreptele BD si CE se
intersecteaza in P. Sa
se arate ca :
[AM]. Dreptele BD si CE se
intersecteaza in P. Sa
se arate ca :
i) Triunghiul PBC
este isoscel ;
ii) PM
este mediatoarea segmentelor [BC]
si [DE].
- Calculati:
a)
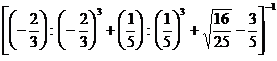 ;
;
b) 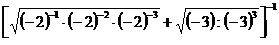 .
.
- Aflati
masurile unghiurilor unui triunghi ABC stiind ca:
 ,unde a, b si c sunt lungimile laturilor BC,
AC, respective AB.
,unde a, b si c sunt lungimile laturilor BC,
AC, respective AB.
Care
este exponentul lui 2 in descompunerea in factori primi a produsului :
31 32
33 . 59 60 ?
Sa
se determine valoarea minima si maxima a expresiei
numerice :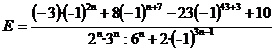 , unde n
, unde n N*.
N*.
Pe
prelungirea coardei [AB] din
cercul de centru O se ia [BC]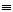 [AO], prelungirea
lui CO taie cercul in E. Aratati ca
[AO], prelungirea
lui CO taie cercul in E. Aratati ca  .
.
Se
da prisma triunghiulara ABCA'B'C'
si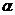 un plan care trece prin A
si intersecteaza muchiile laterale (BB') si (CC') in
punctele D, respectiv E. Aratati ca : SABD + SABC = SECBD.
un plan care trece prin A
si intersecteaza muchiile laterale (BB') si (CC') in
punctele D, respectiv E. Aratati ca : SABD + SABC = SECBD.
- Suma a
doua numere rationale este 2, iar produsul lor este
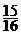 . Aflati
suma inverselor lor.
. Aflati
suma inverselor lor.
- a) Sa
se determine numerele naturale prime a,
b, c stiind ca
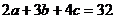 ;
;
b) Un burete de 2 kg
contine 99% apa. Aflati masa buretelui dupa o perioada
de evaporare,
stiind ca
dupa aceasta perioada, el contine 98% apa.
- Lungimea
unui cerc este
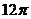 cm. Aflati :
cm. Aflati :
a) aria cercului ;
b) aria patratului inscris in
cerc ;
c) latura si apotema triunghiului echilateral
inscris in cerc.
- Aflati functia f : R
 R care verifica egalitatea:
R care verifica egalitatea: 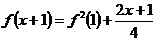 .
.
- Numerele
1330 si 344 dau resturile 10 si respectiv 8 la
impartirea cu acelasi numar a. Aflati toate valorile lui a.
- 4
muncitori pot termina o lucrare in 2 zile, lucrand la acea lucrare cate 4
ore pe zi. In cate zile vor termina acea lucrare 2 muncitori care vor
lucra 8 ore pe zi.
- In
triunghiul
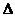 ABC, D
ABC, D (AB), E
(AB), E (AC), DE║BC, DB = 6 cm, AE = 5 cm, AC = 15 cm.
(AC), DE║BC, DB = 6 cm, AE = 5 cm, AC = 15 cm.
Se cer AD si EC.
- Sa se
determine m
 R astfel ca ecuatia :
R astfel ca ecuatia : 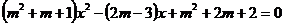 sa admita radacina x = 1. Aflati apoi si
cealalta radacina.
sa admita radacina x = 1. Aflati apoi si
cealalta radacina.
TESTUL C 33
- Se dau
multimile : A = si B
= .
Calculati : A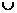 B ; A
B ; A B; A - B
si B - A.
B; A - B
si B - A.
- In
triunghiul ABC, fie mediana [AD], D
 (BC) si [BM] mediana triunghiului ABD, M
(BC) si [BM] mediana triunghiului ABD, M (AD).
Daca aria triunghiului ABC
este de 60 cm2, atunci aflati ariile triunghiurilor ADC si BMD.
(AD).
Daca aria triunghiului ABC
este de 60 cm2, atunci aflati ariile triunghiurilor ADC si BMD.
- Aflati
x
 Z astfel incat
Z astfel incat 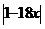 <
<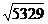 .
.
- Se
considera o piramida hexagonala regulata avand aria
bazei
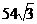 cm2 si inaltimea de 4 cm.
cm2 si inaltimea de 4 cm.
a) Sa se afle aria
laterala a piramidei triunghiulare, care are acelasi varf cu
piramida
hexagonala si
ca baza un triunghi ce se obtine unind din doua in doua
varfurile hexagonului de
baza ;
b) Sa se afle cat la
suta din volumul piramidei hexagonale, reprezinta diferenta
volumelor celor
doua piramide.
- Aratati
ca numarul
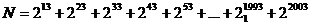 este divizibil cu
103.
este divizibil cu
103.
- Rezolvati
ecuatia :
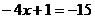 si aflati n
si aflati n Z astfel incat
Z astfel incat 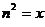 .
.
- Cum se
poate obtine, prin amestecul unor cantitati de acid
sulfuric cu concentratiilor de 20% si 38%, trei litri de acid cu
concentratia de 32% ?
- Rezolvati
ecuatiile :
a)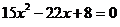 ; b)
; b)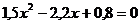 ; c)
; c)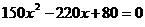 ; Ce se observa ?
; Ce se observa ?
- Determinati
numerele naturale a, b pentru care avem :
i) (a;b) = 28; [a;b] = 980; ii) [a;b] = 720; a b = 34560;
iii) (a;b) = 15; a b = 6300; iv) (a;b) = 18; a + b = 180.
- Raportul
dintre complementul si suplementul unui unghi este
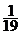 . Aflati masura unghiului.
. Aflati masura unghiului.
- Aflati
A
 B, A
B, A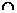 B, A - B si B - A, unde A = si B = .
B, A - B si B - A, unde A = si B = .
- Fie f : R
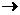 R data de relatia:
R data de relatia: 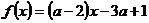 ; a
; a R. Aratati ca oricare ar fi a
R. Aratati ca oricare ar fi a R , graficele acestei functii trec
printr-un acelasi punct.
R , graficele acestei functii trec
printr-un acelasi punct.
- a)
Aratati ca 5 | n,
unde
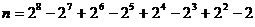 ;
;
b)
Aratati ca 15 | a,
unde 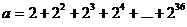 .
.
- Un ceas
indica ora 14 si 30 minute. Masura unghiului format de acul
orar si cel minutar este de : a) 60 ; b) 95 ; c) 105 ; d) 120.
- Rezolvati
ecuatia :
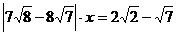 .
.
- Raza,
inaltimea si generatoarea unui con (in aceasta ordine)
au lungimile exprimate prin trei numere naturale consecutive. Aflati
inaltimea unui cilindru care are aceeasi raa cu a
conului si volumul de 4 ori mai mare.
- Aratati
ca urmatoarele fractii sunt ireductibile : a)
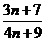 ; b)
; b) 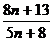 ; c)
; c) 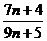 .
.
- Fie ABCD un patrat,
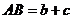 ,
,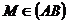 ,
,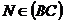 ,
,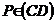 ,
,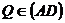 ,
, 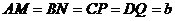 . Se cere. a) MNPQ
este patrat ; b)
. Se cere. a) MNPQ
este patrat ; b)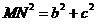 .
.
- Calculati :
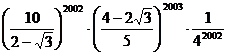 .
.
- Un trunchi
de con are aria bazei mari de 4 ori mai mare decat aria bazei mici.
Sa se afle raportul dintre volumul trunchiului si volumul
conului din care provine trunchiul.
- Aflati
numerele naturale x si y stiind ca diferenta dintre x si y este 2 si
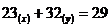 .
.
- Fie
numerele naturale a, b si c proportionale cu 2, 3 si 5.
a)
Aratati ca bc - ab si bc + ac sunt patrate
perfecte ;
b)
Daca ab + ac = bc + 4, aflati a, b,
c.
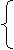 Se considera E(n) = 2n + 3 , pentru n par
Se considera E(n) = 2n + 3 , pentru n par
, pentru n impar
Calculati suma 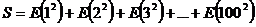 .
.
4. Stiind ca o
prisma are 2350 de diagonale, sa se determine numarul laturilor
poligonului convex
de la baza ei.
- Aflati
numarul natural x pentru care are loc egalitatea :
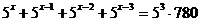 .
.
- Calculati:
a)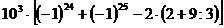 ;
;
b) 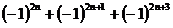 , n
, n N;
N;
c) 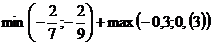 .
.
- Aratati
ca paralela dusa prin punctul de intersectie a diagonalelor
unui trapez oarecare are lungimea egala cu media armonica a
lungimilor bazelor trapezului.
- Doi
cilindri circulari drepti au acelasi volum, razele si
inaltimile fiind diferite. Sa se demonstreze ca
inaltimile lor sunt invers proportionale cu patratele
razelor lor.
- Calculati :
a)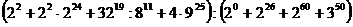 ;
;
b)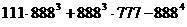 ;
;
- Sa se
afle masurile a doua unghiuri adiacente stiind ca
dublul masurii primului este cat triplul masurii celui de-al
doilea si ca masura unghiului format de bisectoarele lor
este de 20.
- Aratati
ca inaltimea unui trapez dreptunghic cu diagonalele
perpendiculare este medie geometrica intre lungimile bazelor
trapezului.
- Fie
ABCDA'B'C'D' un cub.
a) Aratati ca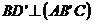 ;
;
b) Aflati distanta de la centrul
fetei ABB'A' la diagonala AC'.
![]()
![]()
![]() - (33 25)6 : (317
230) + 3 (5 + 2 3 - 2430 : 405).
- (33 25)6 : (317
230) + 3 (5 + 2 3 - 2430 : 405).![]() al triunghiului ABC intersecteaza (BC) in D. Fie
al triunghiului ABC intersecteaza (BC) in D. Fie ![]() si
si ![]() astfel incat
astfel incat ![]() si
si ![]() . Daca
. Daca ![]() , demonstrati ca :
, demonstrati ca :![]() isoscel ;
isoscel ; ![]() isoscel.
isoscel.![]() si
si ![]() .
.![]() unde
unde ![]() R.
R.![]()
![]() ,
, ![]() = 20.Pe latura AC se considera punctele M si E astfel incat
= 20.Pe latura AC se considera punctele M si E astfel incat ![]() = 20,
= 20, ![]() = 20, iar pe latura AB se ia punctul N astfel incat
= 20, iar pe latura AB se ia punctul N astfel incat ![]() =
= ![]() este
echilateral ;
este
echilateral ;![]() ; b) card
; b) card![]()
![]() BAC al triunghiului
BAC al triunghiului
![]() ABC si E mijlocul laturii [AC]. Stiind ca
ABC si E mijlocul laturii [AC]. Stiind ca ![]() si DE║ AB, sa se calculeze masurile unghiurilor triunghiului.
si DE║ AB, sa se calculeze masurile unghiurilor triunghiului.![]() . Sa se afle numarul intreg n
. Sa se afle numarul intreg n![]() Z astfel incat N sa
Z astfel incat N sa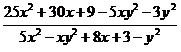 .
.![]() ,
, ![]() si
si![]() sunt invers proportionale cu 0,(3) ; 0,25 si
0,2.
sunt invers proportionale cu 0,(3) ; 0,25 si
0,2.![]() calculati x, y
si z.
calculati x, y
si z.![]() , unde x
, unde x![]() R.
R.![]() ABC cu [AB]
ABC cu [AB]![]() [AC]. Fie [AD] mediana corespunzatoare laturii
[BC], [AE bisectoarea unghiului
[AC]. Fie [AD] mediana corespunzatoare laturii
[BC], [AE bisectoarea unghiului ![]() BAD, E
BAD, E![]() (BC), iar AF
este bisectoarea unghiului
(BC), iar AF
este bisectoarea unghiului ![]() DAC, F
DAC, F![]() (BC).
(BC).![]() .
.![]() R x R pentru care avem:
R x R pentru care avem:![]() m. Aflati
capacitatea in litri a acestui cub.
m. Aflati
capacitatea in litri a acestui cub.![]()
![]() ;
;![]()
![]() cm. Cat de mare trebuie sa fie
cm. Cat de mare trebuie sa fie ![]() cm3?
cm3? 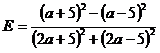 si sa se arate ca
si sa se arate ca![]() .
.![]() .
.![]() = 120 si VA = VB
= VC.
= 120 si VA = VB
= VC. 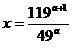
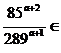 N.
N.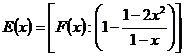
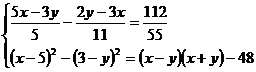 b)
b) ![]()
![]() BC= = , calculati OC si OD.
BC= = , calculati OC si OD.![]() cm2.
cm2.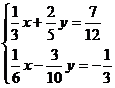 b)
b) 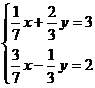
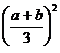
![]() .
.![]() si
si![]() .
.![]() ; ii)
; ii) ![]() .
.![]() BC;
BC;![]() BAD) si cos(
BAD) si cos(![]() ACD).
ACD).![]() R, pentru care functia este
descrescatoare ;
R, pentru care functia este
descrescatoare ;![]() ;
;![]() ;
;![]() .
.![]() ;
; ![]() si
si ![]() .
.![]() calculati x din
calculati x din 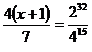
![]() .
.![]() Doua coarde ale unui cerc AB si CD se
intersecteaza in exteriorul cercului in punctul O, A
Doua coarde ale unui cerc AB si CD se
intersecteaza in exteriorul cercului in punctul O, A![]() (OB)
si C
(OB)
si C![]() (OD). Daca
(OD). Daca ![]() = 30, atunci :
= 30, atunci :![]()
![]() i) Aflati
m(BD) si masura
unuia dintre unghiurile formate de BC
si AD, pentru care
i) Aflati
m(BD) si masura
unuia dintre unghiurile formate de BC
si AD, pentru care![]() R x R pentru care xy - 3x = 7 si x2y - 9x
= 175.
R x R pentru care xy - 3x = 7 si x2y - 9x
= 175.![]() AOC si
AOC si ![]() COB doua
unghiuri adiacente suplementare, care se impart in cate trei parti
congruente prin semidreptele [OM, [ON, [OP
si [OQ (in aceasta ordine).
Se cer masurile unghiurilor
COB doua
unghiuri adiacente suplementare, care se impart in cate trei parti
congruente prin semidreptele [OM, [ON, [OP
si [OQ (in aceasta ordine).
Se cer masurile unghiurilor ![]() NOP si
NOP si ![]() MOQ.
MOQ.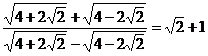 .
.![]() , calculati
, calculati ![]()
![]() ;
;![]() ,
, ![]() , A - B si B -A unde A = si B
, A - B si B -A unde A = si B ![]() AC si VA║ (MBD);
AC si VA║ (MBD);![]() BD = , calculati DM + VO + CM;
BD = , calculati DM + VO + CM;![]() VBC.
VBC.![]() ACB, D
ACB, D![]() (AB). Sa se
afle aria triunghiului CAD.
(AB). Sa se
afle aria triunghiului CAD.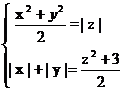
![]() .
.![]() atunci paralelipipedul dreptunghic ABCDA'B'C'D' este cub, unde AB
= a, BC = b si CC' = c.
atunci paralelipipedul dreptunghic ABCDA'B'C'D' este cub, unde AB
= a, BC = b si CC' = c. ![]() ;
;![]() ;
;![]() .
.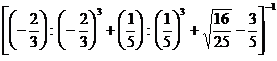 ;
; ![]() .
. 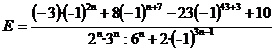 , unde n
, unde n![]() N*.
N*.![]() [AO], prelungirea
lui CO taie cercul in E. Aratati ca
[AO], prelungirea
lui CO taie cercul in E. Aratati ca ![]() .
.![]() un plan care trece prin A
si intersecteaza muchiile laterale (BB') si (CC') in
punctele D, respectiv E. Aratati ca : SABD + SABC = SECBD.
un plan care trece prin A
si intersecteaza muchiile laterale (BB') si (CC') in
punctele D, respectiv E. Aratati ca : SABD + SABC = SECBD.![]() B ; A
B ; A![]() B; A - B
si B - A.
B; A - B
si B - A.![]() ; b)
; b)![]() ; c)
; c)![]() ; Ce se observa ?
; Ce se observa ?![]() .
.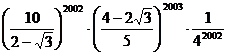 .
.![]() Se considera E(n) = 2n + 3 , pentru n par
Se considera E(n) = 2n + 3 , pentru n par![]() .
.![]() ;
; ![]() , n
, n![]() N;
N;![]() .
.![]() ;
;![]() ;
;![]() ;
;
![]()