| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Exercitii si probleme rezolvate
1. Se aruncǎ o monedǎ de trei ori. Sǎ se determine
a)
Spatiul
![]() al probelor,
al probelor,
b) probele care favorizeazǎ aparitia
evenimentelor: ![]() - ca la prima aruncare sa se obtinǎ marca,
- ca la prima aruncare sa se obtinǎ marca, ![]() - la ultimele douǎ aruncǎri sǎ se obtinǎ marca, respectiv
- la ultimele douǎ aruncǎri sǎ se obtinǎ marca, respectiv ![]() - marca sǎ aparǎ o singurǎ datǎ in cele trei
aruncǎri,
- marca sǎ aparǎ o singurǎ datǎ in cele trei
aruncǎri,
c)
c)evenimentele
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
d) probabilitǎtile evenimentelor precizate la punctele precedente.
Solutie. a)
Dacǎ notǎm prin ![]() aparitia
fetei cu marca (valoarea monedei) la o aruncare si prin
aparitia
fetei cu marca (valoarea monedei) la o aruncare si prin ![]() aparitia
fetei opuse, atunci spatiul
aparitia
fetei opuse, atunci spatiul ![]() al probelor este
al probelor este
![]() .
.
Asadar, spatiul ![]() are 8 probe.
are 8 probe.
b) Probele care favorizeazǎ
aparitia evenimentului ![]() , care inseamnǎ
cǎ la prima aruncare apare marca sunt:
, care inseamnǎ
cǎ la prima aruncare apare marca sunt: ![]()
![]()
![]()
![]() , adicǎ
, adicǎ
![]() .
.
In mod analog, avem cǎ
![]()
![]() .
.
c)
Evenimentul ![]() inseamnǎ cǎ marca apare la prima
aruncare sau o singurǎ datǎ in cele trei aruncǎri, adicǎ
inseamnǎ cǎ marca apare la prima
aruncare sau o singurǎ datǎ in cele trei aruncǎri, adicǎ
![]() .
.
Evenimentul ![]() este evenimentul ca
marca sǎ aparǎ in toate cele trei aruncǎri, adicǎ
este evenimentul ca
marca sǎ aparǎ in toate cele trei aruncǎri, adicǎ ![]() .
.
Evenimentul ![]() inseamnǎ aparitia mǎrcii numai la prima aruncare,
adicǎ
inseamnǎ aparitia mǎrcii numai la prima aruncare,
adicǎ ![]()
Evenimentul ![]() este evenimentul
imposibil, deci
este evenimentul
imposibil, deci ![]() , adicǎ evenimentele
, adicǎ evenimentele ![]() si
si ![]() sunt incompatibile.
sunt incompatibile.
Deoarece ![]() , rezultǎ cǎ
, rezultǎ cǎ ![]() .
.
Evenimentele, ![]() ,
, ![]() , si
, si ![]() , inseamnǎ respectiv cǎ la prima aruncare se
obtine
, inseamnǎ respectiv cǎ la prima aruncare se
obtine ![]() , la ultimele douǎ aruncǎri se obtine cel putin odatǎ
, la ultimele douǎ aruncǎri se obtine cel putin odatǎ ![]() , marca nu apare o singurǎ datǎ in cele trei
aruncǎri. Astfel, putem scrie
, marca nu apare o singurǎ datǎ in cele trei
aruncǎri. Astfel, putem scrie
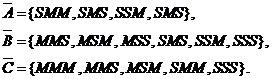
Evenimentul diferentǎ ![]() inseamnǎ cǎ
la prima aruncare apare marca si cǎ
marca apare cel putin de douǎ ori, adicǎ
inseamnǎ cǎ
la prima aruncare apare marca si cǎ
marca apare cel putin de douǎ ori, adicǎ
![]()
Evenimentul diferenta ![]() inseamnǎ cǎ
la prima aruncare apare marca si cǎ
marca apare cel mult douǎ ori, adicǎ
inseamnǎ cǎ
la prima aruncare apare marca si cǎ
marca apare cel mult douǎ ori, adicǎ
![]()
Evenimentul diferentǎ ![]() inseamnǎ cǎ
marca apare o singurǎ datǎ, dar nu la prima aruncare, deci
inseamnǎ cǎ
marca apare o singurǎ datǎ, dar nu la prima aruncare, deci
![]()
d) Folosim definitia
calasicǎ a probabilitǎtii. Pentru aceasta avem cǎ
numǎrul cazurilor posibile este dat de numǎrul probelor lui ![]() , adicǎ 8.
, adicǎ 8.
Numǎrul cazurilor favorabile
evenimentului ![]() este 4, prin urmare se
obtine cǎ
este 4, prin urmare se
obtine cǎ ![]()
Analog avem cǎ
![]()
![]()
![]()
De asemenea avem cǎ
![]() sau folosind formula
sau folosind formula
![]()
In mod analog, ![]()
La fel, avem cǎ ![]() si
si ![]()
2. Un aparat este format din trei componenete.
Se noteazǎ cu ![]() ,
, ![]() si
si ![]() respectiv evenimentele
ca prima, a doua si a treia componentǎ sǎ fie defectǎ.
Sǎ se exprime cu ajutorul evenimentelor
respectiv evenimentele
ca prima, a doua si a treia componentǎ sǎ fie defectǎ.
Sǎ se exprime cu ajutorul evenimentelor ![]() ,
, ![]() si
si ![]() evenimentul ca:
evenimentul ca:
a) cel putin o componentǎ este defectǎ,
b) exact o componentǎ este defectǎ,
c) nici o componenta nu este defectǎ,
d) toate componentele sunt defecte.
Solutie. a)
Dacǎ ![]() este evenimentul ca
cel putin o componentǎ sǎ fie defectǎ, atunci
este evenimentul ca
cel putin o componentǎ sǎ fie defectǎ, atunci ![]() , adicǎ sau prima componentǎ este defectǎ, sau
a doua componentǎ sǎ fie defectǎ, sau a treia componentǎ
sǎ fie defectǎ, ceea ce nu exclude cǎ douǎ sau trei
componente sunt defecte.
, adicǎ sau prima componentǎ este defectǎ, sau
a doua componentǎ sǎ fie defectǎ, sau a treia componentǎ
sǎ fie defectǎ, ceea ce nu exclude cǎ douǎ sau trei
componente sunt defecte.
b) Evenimentul ![]() ca exact o
componentǎ sǎ fie defectǎ se realizeazǎ dacǎ prima
componentǎ este defectǎ si
celelalte douǎ nu sunt defecte, sau a doua componentǎ este defectǎ si celelalte douǎ nu sunt defecte,
sau a treia este defectǎ si
celelale douǎ nu sunt defecte, adicǎ
ca exact o
componentǎ sǎ fie defectǎ se realizeazǎ dacǎ prima
componentǎ este defectǎ si
celelalte douǎ nu sunt defecte, sau a doua componentǎ este defectǎ si celelalte douǎ nu sunt defecte,
sau a treia este defectǎ si
celelale douǎ nu sunt defecte, adicǎ
![]()
c) Evenimentul ![]() ca nici o
componentǎ sǎ nu fie defectǎ, adicǎ fiecare componentǎ
sǎ fie bunǎ, se poate exprima prin
ca nici o
componentǎ sǎ nu fie defectǎ, adicǎ fiecare componentǎ
sǎ fie bunǎ, se poate exprima prin ![]() sau
sau ![]()
d) Evenimentul ![]() ca toate cele trei
componente sǎ fie defecte are exprimarea
ca toate cele trei
componente sǎ fie defecte are exprimarea ![]()
3. Pe un raft sunt asezate la intamplare 10 cǎrti, dintre care trei reprezintǎ cele trei volume ale aceluiasi roman. Sǎ se calculeze probabilitatea ca:
a) cele trei volume ale romanului sǎ fie asezate unul langa altul in ordinea naturalǎ (vol.1,2,3),
b) cele trei volume ale romanului sǎ fie asezate unul langǎ altul in orice ordine,
c) cele trei volume ale romanului sǎ fie asezate unul langǎ altul in ordinea naturalǎ, la inceputul raftului.
Solutie. Numǎrul cazurilor posibile este dat de numǎrul total al modurilor de aranjare a celor 10 cǎrti de pe raft, adic
a) Dacǎ ![]() este evenimentul ca
cele trei volume sǎ fie asezate
unul dupǎ altul in ordine naturalǎ, atunci pentru a stabili cazurile
favorabile, considerǎm cele trei volume ca o singurǎ carte. In acest
fel, numǎrul cazurilor favorabile evenimentului
este evenimentul ca
cele trei volume sǎ fie asezate
unul dupǎ altul in ordine naturalǎ, atunci pentru a stabili cazurile
favorabile, considerǎm cele trei volume ca o singurǎ carte. In acest
fel, numǎrul cazurilor favorabile evenimentului ![]() este dat de
numǎrul modurilor de aranjare a celor 8 cǎrti pe raft (cele 7 rǎmase la care se adaugǎ una
formatǎ din cele trei volume), adicǎ 8! Prin urmare, avem cǎ
este dat de
numǎrul modurilor de aranjare a celor 8 cǎrti pe raft (cele 7 rǎmase la care se adaugǎ una
formatǎ din cele trei volume), adicǎ 8! Prin urmare, avem cǎ ![]()
b) Notǎm cu ![]() evenimentul ca cele
trei volume sǎ fie asezate
unul langǎ altul in orice ordine. Se repetǎ rationamentul de la punctul precedent, cu observatia cǎ 8!
se va inmulti cu 3!, ceea ce reprezintǎ in cate moduri se pot
aseza cele trei volume unul langǎ altul. Asadar obtinem,
cǎ
evenimentul ca cele
trei volume sǎ fie asezate
unul langǎ altul in orice ordine. Se repetǎ rationamentul de la punctul precedent, cu observatia cǎ 8!
se va inmulti cu 3!, ceea ce reprezintǎ in cate moduri se pot
aseza cele trei volume unul langǎ altul. Asadar obtinem,
cǎ ![]()
c) Fie ![]() evenimentul ca cele
trei volume sǎ fie asezate la
inceputul raftului, in ordine naturalǎ. Deoarece "cartea" formatǎ din
cele trei volue este asezatǎ la inceputul raftului, numǎrul
cazurilor favorabile evenimentului
evenimentul ca cele
trei volume sǎ fie asezate la
inceputul raftului, in ordine naturalǎ. Deoarece "cartea" formatǎ din
cele trei volue este asezatǎ la inceputul raftului, numǎrul
cazurilor favorabile evenimentului ![]() este dat de
numǎrul modurilor de aranjare pe raft a celor 7 cǎrti rǎmase, adicǎ 7!. Astfel,
rezultǎ cǎ
este dat de
numǎrul modurilor de aranjare pe raft a celor 7 cǎrti rǎmase, adicǎ 7!. Astfel,
rezultǎ cǎ ![]()
4. Cu ocazia sǎrbǎtorilor de iarnǎ, la un magazin cu dulciuri sunt pregǎtite pachete pentru copii. Stiind cǎ pentru pregǎtirea unui pachet se dispune de ciocolatǎ in 6 sortimente, cutii cu bomboane in 10 sortimente si cutii cu biscuiti in 9 sortimente si cǎ in fiecare pachet se pun la intamplare 5 sortimente de dulciuri(ciocolatǎ, bomboane, biscuiti), sǎ se determine probabilitatea ca un pachet luat la intamplare sǎ contin
a) douǎ ciocolate, douǎ cutii cu bomboane si o cutie cu biscuiti(toate de sortimente diferite),
b) trei ciocolate si douǎ cutii cu bomboane.
Solutie.
Numǎrul total de
sortimente de dulciuri de care se dispune pentru formarea unui pachet este 25,
iar pentru fiecare pachet se ia la intamplare 5 sortimente de dulciuri. Prin urmare, numǎrul total
a modurilor de formare a unui pachet este ![]() si care
reprezintǎ numǎrul cazurilor posibile.
si care
reprezintǎ numǎrul cazurilor posibile.
a) Dacǎ ![]() este evenimentul ca
pachetul sǎ continǎ
douǎ ciocolate, douǎ cutii de bomboane si o cutie de
biscuiti, atunci numǎrul cazurilor favorabile acestui eveniment este
este evenimentul ca
pachetul sǎ continǎ
douǎ ciocolate, douǎ cutii de bomboane si o cutie de
biscuiti, atunci numǎrul cazurilor favorabile acestui eveniment este ![]() . Intr-adevǎr, cele douǎ ciocolate de sortimente
diferite se pot lua din cele 6 sortimente in
. Intr-adevǎr, cele douǎ ciocolate de sortimente
diferite se pot lua din cele 6 sortimente in ![]() . La fel se rationeazǎ pentru cele douǎ
sortimente de bomboane si pentru cutia de biscuiti. Rezultǎ
cǎ
. La fel se rationeazǎ pentru cele douǎ
sortimente de bomboane si pentru cutia de biscuiti. Rezultǎ
cǎ
![]()
b) Fie ![]() evenimentul ca
pachetul sǎ continǎ
trei ciocolate de sortimente diferite si douǎ cutii cu bomboane de
sortimente diferite. Rationand ca mai inainte, se obtine cǎ
evenimentul ca
pachetul sǎ continǎ
trei ciocolate de sortimente diferite si douǎ cutii cu bomboane de
sortimente diferite. Rationand ca mai inainte, se obtine cǎ
![]()
5. Se aruncǎ trei zaruri, fiecare avand o fata coloratǎ alb, una coloratǎ negru si cate douǎ colorate in rosu si respectiv in galben. Sǎ se determine probabilitatea ca:
a) cel putin un zar sǎ arate culoarea rosie,
b) cel putin douǎ zaruri sǎ arate culoarea albǎ.
Solutie. Fie ![]() evenimentul ca cel
putin unul din cele trei zaruri sǎ arate culoarea rosie. Dacǎ se
noteazǎ cu
evenimentul ca cel
putin unul din cele trei zaruri sǎ arate culoarea rosie. Dacǎ se
noteazǎ cu ![]() evenimentul ca zarul
evenimentul ca zarul ![]() aratǎ culoarea rosie, atunci
aratǎ culoarea rosie, atunci ![]() , unde evenimentele reuniunii sunt independente. Prin urmare,
folosind formula lui Poincar, se obtine c
, unde evenimentele reuniunii sunt independente. Prin urmare,
folosind formula lui Poincar, se obtine c
![]()
Deoarece zarurile
sunt identice, avem ![]() , deci
, deci
![]()
b) Fie ![]() evenimentul ca cel
putin douǎ zaruri sǎ arate culoarea albǎ, atunci
evenimentul ca cel
putin douǎ zaruri sǎ arate culoarea albǎ, atunci ![]() este evenimentul ca
cel putin un zar sǎ arate culoarea albǎ. Daca notǎm cu
este evenimentul ca
cel putin un zar sǎ arate culoarea albǎ. Daca notǎm cu
![]() evenimentul ca nici un
zar sǎ nu arate culoarea albǎ, respectiv prin
evenimentul ca nici un
zar sǎ nu arate culoarea albǎ, respectiv prin ![]() evenimentul ca exact
un zar din cele trei sǎ arate culoarea albǎ, atunci
evenimentul ca exact
un zar din cele trei sǎ arate culoarea albǎ, atunci ![]() . Deoarece evenimentele
. Deoarece evenimentele ![]() si
si ![]() sunt incompatibile,
avem cǎ
sunt incompatibile,
avem cǎ ![]()
Pe de altǎ parte, se obtine cǎ ![]() , iar
, iar ![]() . Prin urmare, avem cǎ
. Prin urmare, avem cǎ ![]() , de unde
, de unde ![]()
Dacǎ o familie are 5 copii, se cere sǎ se calculeze probabilitatea ca:
a) patru din cei cinci copii sǎ fie bǎieti,
b) b)cel putin doi din cei cinci copii sǎ fie bǎieti.
Solutie.
Pentru rezolvarea problemei
se aplicǎ schema lui Bernoulli cu bila intoarsǎ, unde ![]() ,
, ![]() .
.
a)
Fie ![]() evenimentul ca familia sǎ
aibǎ exact patru bǎieti. Luand
evenimentul ca familia sǎ
aibǎ exact patru bǎieti. Luand ![]() in schema lui
Bernoulli cu bila intoarsǎ, rezultǎ cǎ
in schema lui
Bernoulli cu bila intoarsǎ, rezultǎ cǎ
![]()
b) Dacǎ notǎm
cu ![]() evenimentul ca familia sǎ aibǎ cel
putin doi bǎieti,
atunci
evenimentul ca familia sǎ aibǎ cel
putin doi bǎieti,
atunci ![]() este evenimentul ca familia sǎ aibǎ un bǎiat
sau nici unul. Prin urmare, se poate scrie
este evenimentul ca familia sǎ aibǎ un bǎiat
sau nici unul. Prin urmare, se poate scrie
![]()
Asadar, avem cǎ
![]()
7. La un magazin se gǎsesc articole de imbrǎcaminte dintre care 90% satisfac standardele, 7% prezintǎ defectiuni retusabile, iar 3% prezintǎ defectiuni neretusabile. Sǎ se calculeze probabilitatea ca din sase articole luate la intamplare, trei sǎ satisfacǎ standardele, douǎ sǎ fie retusabile si unul sǎ fie neretusabil.
Solutie. Rezolvarea
se bazeazǎ pe schema lui Bernoulli cu bila intoarsǎ cu mai multe
stǎri (trei), unde ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Astfel se obtine probabilitatea cerutǎ ca fiind
![]()
8. Pe un raft, intr-un magazin, se aflǎ 50 de piese de acelasi tip, care provin de la douǎ fabrici, respectiv 20 de la una dintre ele si 30 de la cealaltǎ. Intr-o zi s-au vandut sase astfel de piese. Sǎ se calculeze probabilitatea sǎ se fi vandut acelasi numǎr (cate trei) de piese de la cele douǎ fabrici.
Solutie. Se
aplicǎ schema lui Bernoulli cu bila neintoarsǎ, unde ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Prin urmare, probabilitatea cerutǎ este
. Prin urmare, probabilitatea cerutǎ este
![]()
9. Intr-o cutie sunt 12 bile marcate cu 1, 8 sunt marcate cu 3 si 6 cu 5. O persoanǎ extrage la intamplare din cutie 4 bile. Sǎ se calculeze probabilitatea ca suma obtinutǎ sǎ fie cel mult 13.
Solutie. Dacǎ
notǎm cu ![]() evenimentul ca suma
obtinutǎ pe cele patru bile sǎ fie cel mult 13, atunci
evenimentul contrar
evenimentul ca suma
obtinutǎ pe cele patru bile sǎ fie cel mult 13, atunci
evenimentul contrar ![]() este evenimentul ca
cele patru bile sǎ fie cel putin 14. Se
vede cǎ suma maximǎ ce se poate obtine este 45=20. De asemenea, avem c 5+13=18, 35+11=16, 25+23=16, 25+13+11=14,
15+33=14. Alte posibilitǎti de a obtine suma cel
putin 14 din patru bile nu existǎ.
este evenimentul ca
cele patru bile sǎ fie cel putin 14. Se
vede cǎ suma maximǎ ce se poate obtine este 45=20. De asemenea, avem c 5+13=18, 35+11=16, 25+23=16, 25+13+11=14,
15+33=14. Alte posibilitǎti de a obtine suma cel
putin 14 din patru bile nu existǎ.
Asadar, pentru a obtine suma 14 trebuie luate douǎ bile marcate cu 5 din cele sase existente, una marcatǎ cu 3 din cele opt si respectiv una marcatǎ cu 1 din cele 12, respectiv una marcatǎ cu 5 si 3 marcate cu 3. Folosind schema lui Bernoulli cu bila neintoarsǎ cu trei stǎri se obtine c
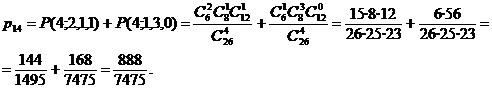
Analog, avem cǎ
![]()
![]()
![]()
Asadar, avem cǎ ![]() , de unde
, de unde ![]()
10. Cinci masini, care produc acelasi tip de piese, dau rebuturi in procente 2%, 1%, 5%, 4%, 6% respectiv. Se ia cate o piesǎ produsǎ de la fiecare. Sǎ se calculeze probabilitatea ca din cele cinci piese luate, exact douǎ sǎ fie rebut, precum si probabilitatea ca cel putin una sǎ fie rebut.
Solutie. Se
aplicǎ schema lui Poisson, unde ![]() , iar
, iar
![]()
Probabilitatea ca din
cele cinci piese douǎ sǎ fie rebut se obtine ca fiind coeficientul lui ![]() al polinomului
al polinomului
![]()
adic
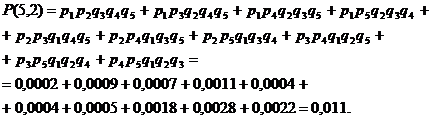
Dacǎ ![]() este evenimentul
ca cel putin una din cele cinci piese sǎ fie rebut, atunci
este evenimentul
ca cel putin una din cele cinci piese sǎ fie rebut, atunci ![]() este evenimentul ca
nici o piesǎ sǎ nu fie defectǎ. Deci
este evenimentul ca
nici o piesǎ sǎ nu fie defectǎ. Deci ![]() , de unde
, de unde ![]()
11. Doi jucǎtori sunt angrenati intr-un
joc format din mai multe partide. Primul jucǎtor castigǎ o partidǎ cu probabilitatea ![]() si o pierde cu
probabilitatea
si o pierde cu
probabilitatea ![]() . Sǎ se calculeze probabilitatea ca:
. Sǎ se calculeze probabilitatea ca:
a) prima partidǎ castigatǎ de primul jucǎtor sǎ se producǎ dupǎ cinci partide pierdute,
b) a treia partidǎ castigatǎ de primul jucǎtor sǎ se producǎ dupǎ un total de sase partide pierdute.
Solutie. a) Se aplicǎ schema geometricǎ. Prin urmare, probabilitatea cerutǎ este datǎ prin
![]()
b) Se utilizeazǎ schema lui
Pascal (binomialǎ cu exponent negativ),unde ![]() ,
, ![]() ,
, ![]() ,
,![]() . Astfel probabilitatea cerutǎ este
. Astfel probabilitatea cerutǎ este
![]()
12. Intr-o cutie se aflǎ 15 mingi de tenis, din care 9 sunt noi. Pentru primul joc sunt luate la intamplare trei mingi, dupǎ care se depun in cutie. Pentru al doilea joc sunt luate din nou trei mingi la intamplare. Sǎ se calculeze probabilitatea ca:
a) pentru jocul al doilea sǎ fie luate trei mingi noi,
b) pentru primul joc sǎ se fi luat trei mingi noi, dacǎ se stie cǎ la jocul al doilea au fost luate trei mingi noi.
Solutie. a)
Notǎm cu ![]() evenimentul ca la
jocul al doilea sǎ fie l;uate trei mingi noi si cu
evenimentul ca la
jocul al doilea sǎ fie l;uate trei mingi noi si cu ![]() evenimentul ca la
primul joc sǎ fie luate
evenimentul ca la
primul joc sǎ fie luate ![]() mingi noi.
Evenimentele
mingi noi.
Evenimentele ![]() ,
, ![]() ,
, ![]() ,
, ![]() formeazǎ un
sistem complet de evenimente. Folosim formula probabilitǎtii totale
formeazǎ un
sistem complet de evenimente. Folosim formula probabilitǎtii totale
![]()
Pe de altǎ parte, folosind schema lui Bernoulli cu bila neintoarsǎ se obtine:
![]() ,
, ![]() ,
,
![]() ,
, ![]()
Deoarece cele trei mingi folosite la primul joc s-au uzat si sunt puse inapoi in cutie, structura cutiei se schimbǎ, cu exceptia cazului cand la primul joc s-au folosit numai mingi uzate. Asadar, probabilitǎtile conditionate din formula probabilitǎtii totale se calculeazǎ tot cu schema lui Bernoulli cu bila neintoarsǎ, adicǎ
![]() ,
, ![]() ,
,
![]() ,
, ![]()
Prin urmare avem cǎ
![]()
b) Cu notatiile de la punctul
precedent, se cere calculatǎ probabilitate conditionatǎ ![]() . Pentru aceasta se foloseste formula lui Bayes, anume
. Pentru aceasta se foloseste formula lui Bayes, anume
![]()
Astfel, se obtine cǎ
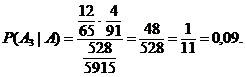
13. Un motor genereazǎ energie
electricǎ ce este folositǎ intermitent de cǎtre 10 muncitori,
care lucreazǎ independent. Fiecare muncitor utilizeazǎ energie timp
de 12 minute intr-o orǎ. Se noteazǎ cu ![]() numǎrul
muncitorilor ce utilizeazǎ energie la un moment dat. Sǎ se scrie
distributia variabilei aleatoare
numǎrul
muncitorilor ce utilizeazǎ energie la un moment dat. Sǎ se scrie
distributia variabilei aleatoare ![]() .
.
Solutie. Valorile
pe care le ia variabila aleatoare ![]() sunt 0,1,,10,
adicǎ la un moment dat se poate ca nici unul din muncitori sǎ nu
foloseascǎ energie, sau unul, sau asa mai departe 10 muncitori sǎ foloseascǎ
energie electricǎ produsǎ de motor.
sunt 0,1,,10,
adicǎ la un moment dat se poate ca nici unul din muncitori sǎ nu
foloseascǎ energie, sau unul, sau asa mai departe 10 muncitori sǎ foloseascǎ
energie electricǎ produsǎ de motor.
Prin urmare,
distributia variabilei aleatoare ![]() este
este
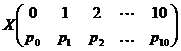 sau prescurtat
sau prescurtat 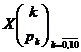 ,
,
unde ![]()
Pentru a calcula probabilitatea ![]() , avem in vedere cǎ un muncitor, la un moment dat,
foloseste energie electricǎ cu
probabilitatea
, avem in vedere cǎ un muncitor, la un moment dat,
foloseste energie electricǎ cu
probabilitatea ![]() (12 minute dintr-o orǎ), iar aceastǎ probabilitate
este aceeasi pentru fiecare din
cei 10 muncitori. Prin urmare, probabilitatea
(12 minute dintr-o orǎ), iar aceastǎ probabilitate
este aceeasi pentru fiecare din
cei 10 muncitori. Prin urmare, probabilitatea ![]() se calculeazǎ cu
ajutorul schemei lui Bernoulli cu bila intoarsǎ, adicǎ
se calculeazǎ cu
ajutorul schemei lui Bernoulli cu bila intoarsǎ, adicǎ
![]() ,
, ![]() ,
, ![]() , sau
, sau
![]() ,
, ![]()
Retinem, deci, cǎ variabila
aleatoare ![]() urmeazǎ legea
binomialǎ.
urmeazǎ legea
binomialǎ.
14. La o unitate hotelierǎ clientii
doresc camere dotate cu televizor sau nu cu aceeasi probabilitate. Se
considerǎ primii patru clienti ai zilei si se noteazǎ cu ![]() si respectiv
si respectiv ![]() respectiv numǎrul
clientilor ce solicitǎ
camerǎ cu televizor si numǎrul maxim ai clientilor consecutiv inregistrati, care
solicitǎ camerǎ cu televizor. Sǎ se scrie distributiile
respectiv numǎrul
clientilor ce solicitǎ
camerǎ cu televizor si numǎrul maxim ai clientilor consecutiv inregistrati, care
solicitǎ camerǎ cu televizor. Sǎ se scrie distributiile
a)
variabilelor aleatoare ![]() si
si ![]() ,
,
b)
vectorul aleator ![]() ,
,
c)
variabilelor aleatoare ![]() si
si ![]() .
.
Solutie.
Pentru a calcula probabilit tile din distributiile variabilelor
aleatoare considerate, vom scrie pentru inceput spatiul probelor. Dacǎ
marcǎm prin ![]() si respectiv prin
N faptul cǎ un client solicitǎ, respectiv nu solicitǎ
camerǎ cu televizor, atunci spatiul
si respectiv prin
N faptul cǎ un client solicitǎ, respectiv nu solicitǎ
camerǎ cu televizor, atunci spatiul ![]() al probelor este
al probelor este
![]()
Deoarece, clientii
preferǎ sau nu televizor cu aceeasi probabilitate, avem cǎ probabilitatea ca un client sǎ
solicite televizor este ![]() si sǎ nu
solicite televizor este
si sǎ nu
solicite televizor este ![]()
a) Valorile pe care le
ia variabila aleatoare ![]() sunt 0, 1, 2, 3, 4,
adicǎ din cei patru clienti pot
dori camerǎ cu televizor 0, 1, 2, 3, respectiv 4 clienti. Asadar
avem cǎ
sunt 0, 1, 2, 3, 4,
adicǎ din cei patru clienti pot
dori camerǎ cu televizor 0, 1, 2, 3, respectiv 4 clienti. Asadar
avem cǎ
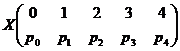 , unde
, unde ![]() ,
,
si care se calculeazǎ cu schema lui Bernoulli cu bila intoarsǎ. Prin urmare, se obtine cǎ
![]() , pentru
, pentru ![]()
Calculand pe rand aceste probabilitǎti, rezultǎ cǎ
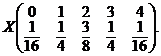
Variabila aleatoare ![]() poate sǎ ia una
din valorile 0, 1, 2, 3, 4, adicǎ din cei patru clienti se poate ca
0, 1, 2, 3, 4 sǎ fie numǎrul maxim al clientilor consecutivi ce solicitǎ camerǎ
cu televizor. Distributia variabilei aleatoare
poate sǎ ia una
din valorile 0, 1, 2, 3, 4, adicǎ din cei patru clienti se poate ca
0, 1, 2, 3, 4 sǎ fie numǎrul maxim al clientilor consecutivi ce solicitǎ camerǎ
cu televizor. Distributia variabilei aleatoare ![]() este
este
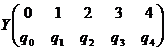 , unde
, unde ![]()
Pentru a calcul probabilitatile distributiei lui ![]() , urmarim spatiul
, urmarim spatiul ![]() al probelor.
al probelor.
De exemplu, evenimentul (![]() ) este favorizat de proba
) este favorizat de proba ![]() , deci
, deci ![]() . Apoi, evenimentul (
. Apoi, evenimentul (![]() ) este favorizat de probele
) este favorizat de probele ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , deci
, deci ![]() . Analog, se obtine ca
. Analog, se obtine ca ![]()
![]() si
si ![]() . Prin urmare, distributia variabilei aleatoare
. Prin urmare, distributia variabilei aleatoare ![]() este
este
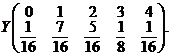
b) Distributia
vectorului ![]() este datǎ prin
tabloul
este datǎ prin
tabloul
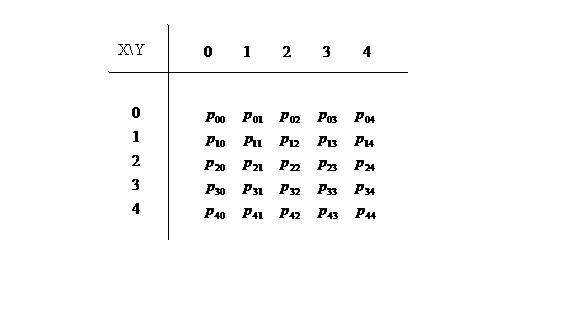
unde ![]() . Pentru a calcula aceste probabilitǎti,
urmǎr,im in spatiul
. Pentru a calcula aceste probabilitǎti,
urmǎr,im in spatiul ![]() al probelor acele
probe care favorizeazǎ evenimentele
al probelor acele
probe care favorizeazǎ evenimentele![]()
Astfel,
evenimentul ![]() este favorizat de proba
este favorizat de proba ![]() , deci
, deci ![]() . Apoi, evenimentul
. Apoi, evenimentul ![]() nu este favorizat de nici o probǎ,
deci
nu este favorizat de nici o probǎ,
deci ![]()
Sǎ mai considerǎm, de
exemplu evenimentul ![]() , care este
favorizat de probele
, care este
favorizat de probele ![]() ,
, ![]() ,
, ![]() , prin urmare
, prin urmare ![]() . Prin rationament analog se obtine tabloul
distributional al vectorului aleator
. Prin rationament analog se obtine tabloul
distributional al vectorului aleator ![]() :
:

Prin calcul direct, se vede c
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
c) Dacǎ variabilele aleatoare ![]() si
si ![]() iau valorile 0, 1, 2,
3 si 4, atunci variabila aleatoare
iau valorile 0, 1, 2,
3 si 4, atunci variabila aleatoare ![]() poate lua una din
valorile 0, 1, , 8. Mai trebuie precizate probabilitǎtile cu care
sunt luate aceste valori. Aceste probabilitǎti se calculeazǎ
dupǎ cum urmeazǎ:
poate lua una din
valorile 0, 1, , 8. Mai trebuie precizate probabilitǎtile cu care
sunt luate aceste valori. Aceste probabilitǎti se calculeazǎ
dupǎ cum urmeazǎ:
![]()
![]()
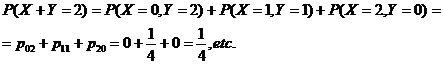
In acest fel se
obtine distributia variabilei aleatoare ![]() , anume
, anume
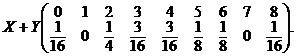
Deoarece ![]() si
si ![]() , deci este imposibil ca
, deci este imposibil ca ![]() sǎ aibǎ
aceste valori, acestea se eliminǎ din tabloul distributional
obtinandu-se
sǎ aibǎ
aceste valori, acestea se eliminǎ din tabloul distributional
obtinandu-se
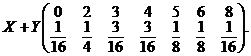
Pentru a scrie distributia
variabilei aleatoare ![]() , se procedeazǎ in mod analog, anume
, se procedeazǎ in mod analog, anume ![]() poate lua una din
valorile 0, 1, 2, 3, 4, 6, 8, 9, 12, 1 De asemenea, probabilitǎtile se calculeazǎ dupǎ cum
urmeazǎ:
poate lua una din
valorile 0, 1, 2, 3, 4, 6, 8, 9, 12, 1 De asemenea, probabilitǎtile se calculeazǎ dupǎ cum
urmeazǎ:
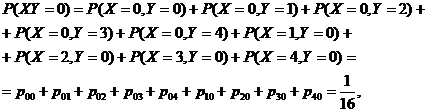
![]() s.a.m d.
s.a.m d.
Se obtine in acest fel distributia vectorului aleator produs
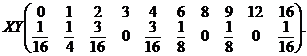
sau
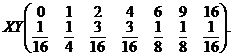
15. La trei unitǎti se gǎsesc
articole ce provin de la douǎ fabrici, in urmǎtoarele proportii: la
prima unitate ![]() de la prima fabricǎ, la a doua unitate
de la prima fabricǎ, la a doua unitate ![]() de la prima
fabricǎ, iar la a treia unitate
de la prima
fabricǎ, iar la a treia unitate ![]() de la prima
fabricǎ. Un client cumpǎrǎ cate un articol de la fiecare
unitate. Fie
de la prima
fabricǎ. Un client cumpǎrǎ cate un articol de la fiecare
unitate. Fie ![]() numǎrul
articolelor cumpǎrate de client si care provin de la fabricǎ.
Sǎ se scrie distributia variabilei aleatoare
numǎrul
articolelor cumpǎrate de client si care provin de la fabricǎ.
Sǎ se scrie distributia variabilei aleatoare ![]() , functia de repartitie corespunzǎtoare lui
, functia de repartitie corespunzǎtoare lui ![]() , iar apoi sǎ se reprezinte grafic functia de
repartitie.
, iar apoi sǎ se reprezinte grafic functia de
repartitie.
Solutie. Variabila
aleatoare ![]() poate lua una din valorile 0, 1, 2, 3, iar
probabilitǎtile cu care sunt luate aceste valori sunt date de schema
lui Poisson, unde
poate lua una din valorile 0, 1, 2, 3, iar
probabilitǎtile cu care sunt luate aceste valori sunt date de schema
lui Poisson, unde ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Prin urmare, variabila aleatoare
. Prin urmare, variabila aleatoare ![]() are distributia
are distributia
![]() ,
,
unde ![]() .
.
Avem pe rand cǎ
![]()
![]()
![]()
![]()
deci distributia variabilei aleatoare ![]() este
este
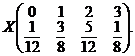
Pornind de la definitia functiei de repartitie se obtine cǎ:
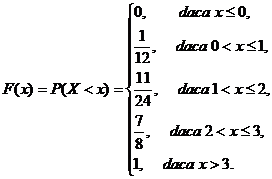
Modul cum a fost
determinatǎ expresia functiei de
repartitie il exemplificǎm prin cazul ![]() . Astfel avem cǎ
. Astfel avem cǎ
![]()
Graficul functiei de repartitie este dat in fig.1.
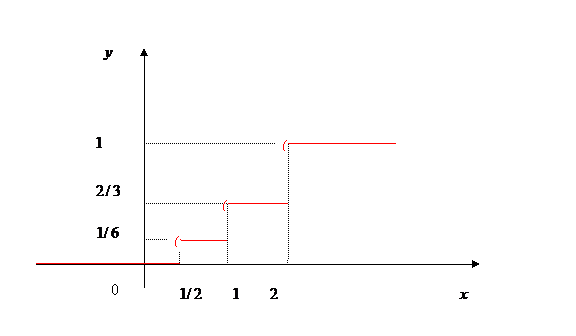
Fig.1
1 Un sofer amator intentioneazǎ
sǎ circule cu masina neinmatriculatǎ panǎ cand va ajunge la a treia
sanctiune primitǎ din partea agentilor de circulatie. Fie ![]() numǎrul zileler in care circulǎ
panǎ la a treia sanctiune. Sǎ se scrie distributia variabilei aleatoare
numǎrul zileler in care circulǎ
panǎ la a treia sanctiune. Sǎ se scrie distributia variabilei aleatoare ![]() , stiind cǎ soferul poate fi controlat in fiecare zi
cu aceeasi probabilitate
, stiind cǎ soferul poate fi controlat in fiecare zi
cu aceeasi probabilitate ![]() , iar apoi sǎ se
scrie functia de repartitie corespunzǎtoare variabilei aleatoare
, iar apoi sǎ se
scrie functia de repartitie corespunzǎtoare variabilei aleatoare ![]()
Solutie. Variabila
aleatoare ![]() poate lua una din
valorile 0, 1, Prin urmare, variabila aleatoare
poate lua una din
valorile 0, 1, Prin urmare, variabila aleatoare ![]() are distributia
are distributia
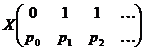 sau prescurtat
sau prescurtat 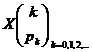
unde ![]() . Probabilitatea
. Probabilitatea ![]() se calculeazǎ folosind
schema lui Pascal cu
se calculeazǎ folosind
schema lui Pascal cu ![]() ,
, ![]() , adicǎ
, adicǎ
![]()
De exemplu, avem cǎ
![]()
![]()
![]()
Functia de
repartitie se scrie pornind de la definitie. Dacǎ ![]() , atunci
, atunci
![]()
Dacǎ ![]() , atunci
, atunci
![]()
Dacǎ ![]() , atunci
, atunci
![]()
In general, dacǎ ![]() , avem cǎ
, avem cǎ
![]()
17. Se considerǎ variabila aleatoare ![]() de tip continuu, care
are densitatea de probabilitate
de tip continuu, care
are densitatea de probabilitate ![]() , pentru orice
, pentru orice ![]() , unde
, unde ![]() este un parametru
real. Sǎ se determine
este un parametru
real. Sǎ se determine
a) parametrul real ![]() ,
,
b) functia de repartitie a variabilei aleatoare ![]() ,
,
c) probabilitǎtile ![]() si
si ![]()
Solutie. a)
Deoarece functia ![]() este o densitate de probabilitate, rezultǎ
cǎ
este o densitate de probabilitate, rezultǎ
cǎ ![]() , de unde
, de unde ![]()
De asemenea, se impune ca
![]()
Observǎm cǎ functia care se integreazǎ este functie parǎ, iar intervalul de integrare este simetric fata de origine, astfel cǎ
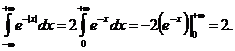
Dacǎ se inlocuieste mai sus, avem cǎ ![]() ,
, ![]() .
.
b) Intre densitatea de probabilitate si functia de reartitie
avem relatia
![]()
Dacǎ ![]() , atunci implicit avem cǎ
, atunci implicit avem cǎ ![]() , deci
, deci
![]()
Dacǎ ![]() , integrala se descompune in suma a douǎ integrale,
anume:
, integrala se descompune in suma a douǎ integrale,
anume:
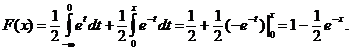
Prin urmare, avem functia de repartitie
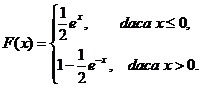
c)Folosind functia de repartitie avem cǎ
![]()
A doua probabilitate este o probabilitate conditionatǎ, prin urmare
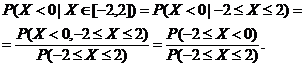
Ca mai inainte, avem cǎ
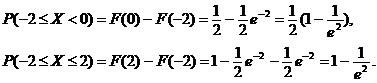
Prin urmare, se obtine cǎ ![]()
18. Vectorul aleator ![]() are densitatea de probabilitate
are densitatea de probabilitate
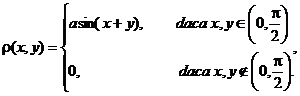
Se cere:
a)
sǎ
se determine constanta ![]() ,
,
b) densitǎtile de probabilitate pentru
variabilele aleatoare componente ![]() si
si ![]() ,
,
c)
probabilitǎtile
![]() si
si ![]()
Solutie. a) Din
proprietǎtile densitǎtii de probabilitate, avem cǎ ![]() , de unde, in mod necesar,
, de unde, in mod necesar, ![]()
Pe de altǎ parte se impune ca
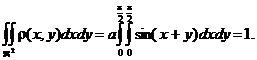
Pentru calculul acestei integrale duble scriem succesiv
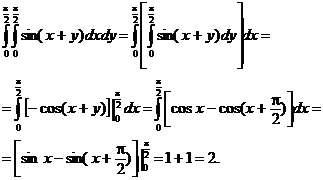
Asadar, avem cǎ ![]() , de unde
, de unde ![]()
b) Pentru determinare
densitǎti de probabilitate ![]() a variabilei aleatoare
a variabilei aleatoare
![]() , folosim formula
, folosim formula
![]() , pentru
, pentru ![]() .
.
Dacǎ ![]() , atunci
, atunci ![]() , deci
, deci ![]()
Dacǎ ![]() , atunci avand in vedere cǎ
, atunci avand in vedere cǎ ![]() , pentru
, pentru ![]() , putem
scrie
, putem
scrie
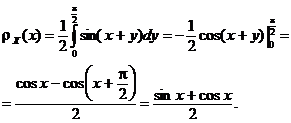
Prin urmare, avem cǎ
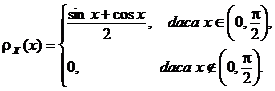
Analog se obtine cǎ
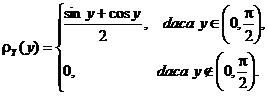
d)Avand in vedere cǎ densitatea
de probabilitate ![]() a vectorului
aleator
a vectorului
aleator ![]() , putem calcula probabilitatea cerutǎ cu formula
, putem calcula probabilitatea cerutǎ cu formula
![]() , unde
, unde ![]()
Astfel avem
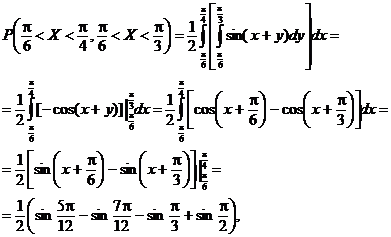
de unde 
Folosind definitia probabilitǎtii conditionate, avem cǎ
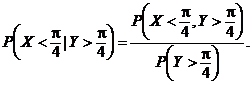
Pe de o parte, avem succesiv
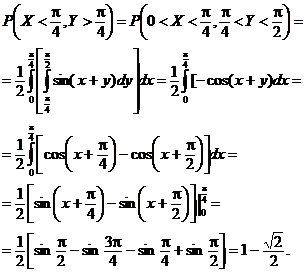
Pe de altǎ parte avem cǎ
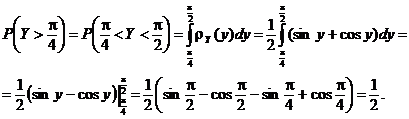
Folosind aceste douǎ probabilitǎti calculate, avem cǎ
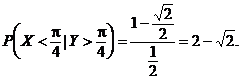
19. Se considerǎ variabila aleatoare ![]() ce urmeaza legea normalǎ
ce urmeaza legea normalǎ ![]() , adicǎ are densitatea de probabilitate
, adicǎ are densitatea de probabilitate
![]() , pentru orice
, pentru orice ![]()
Sǎ se determine densitatea de probabilitate pentru variabilele
aleatoare ![]() ,
,
(![]() ,
, ![]() ) si
) si ![]()
Solutie. Se
stie cǎ dacǎ intre douǎ variabile aleatoare de tip continuu
existǎ o legǎturǎ liniarǎ, adicǎ ![]() (
(![]() ), atunci intre densitǎtile corespunzǎtoare
existǎ relatia
), atunci intre densitǎtile corespunzǎtoare
existǎ relatia ![]()
Deoarece, in cazul de fata, ![]() , iar
, iar ![]() , avem cǎ
, avem cǎ
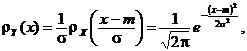
deci variabila aleatoare![]() urmeazǎ legea normalǎ
urmeazǎ legea normalǎ ![]()
Pentru a determina densitatea de
probabilitate ![]() a variabilei aleatoare
a variabilei aleatoare
![]() , determinǎm, prima datǎ functia de repartitie
, determinǎm, prima datǎ functia de repartitie ![]() pentru aceasta. Se
porneste de la definitia functiei de repartitie, adic
pentru aceasta. Se
porneste de la definitia functiei de repartitie, adic
![]()
Deoarece ![]() , rezultǎ cǎ pentru
, rezultǎ cǎ pentru ![]() avem
avem ![]()
Dac ![]() , putem scrie cǎ
, putem scrie cǎ ![]()
Prin derivarea functiei de repartitie se obtine densitatea de probabilitate, adic
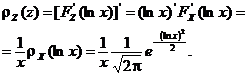
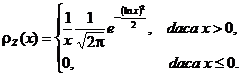 Asadar,
s-a obtinut cǎ
Asadar,
s-a obtinut cǎ
20. La patru unitǎti de oras
consumul de apǎ este normal cu probabilitǎtile 0,9, 0,8, 0,85
si respectiv 0,7. Se noteazǎ cu ![]() numǎrul
unitǎtilor, din cele patru, la care consumul este normal intr-o zi
fixatǎ din sǎptǎmanǎ. Sǎ se scrie distributia
variabilei aleatoare
numǎrul
unitǎtilor, din cele patru, la care consumul este normal intr-o zi
fixatǎ din sǎptǎmanǎ. Sǎ se scrie distributia
variabilei aleatoare ![]() , iar apoi sǎ se
calculeze valoarea medie, dispersia, abaterea standard, mediana si modul
variabilei aleatoare
, iar apoi sǎ se
calculeze valoarea medie, dispersia, abaterea standard, mediana si modul
variabilei aleatoare ![]() .
.
![]()
Solutie.
Variabila aleatoare ![]() poate sǎ ia
una din valorile 0, 1, 2, 3, 4, dupǎ cum numǎrul unitǎtilor
la care consumul este normal, in ziua precizatǎ, este normal in 0, 1, 2,
3,respectiv 4 unitǎti. Prin urmare, variabila aleatoare
poate sǎ ia
una din valorile 0, 1, 2, 3, 4, dupǎ cum numǎrul unitǎtilor
la care consumul este normal, in ziua precizatǎ, este normal in 0, 1, 2,
3,respectiv 4 unitǎti. Prin urmare, variabila aleatoare ![]() are distributia
are distributia
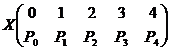 , unde
, unde ![]() ,
, ![]()
Probabilitǎtile ![]() se
calculeazǎ cu schema lui Poisson. Pentru aceasta avem
se
calculeazǎ cu schema lui Poisson. Pentru aceasta avem ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , adicǎ
, adicǎ ![]() este probabilitatea
sǎ fie consumul normal la unitatea
este probabilitatea
sǎ fie consumul normal la unitatea ![]() , iar
, iar ![]() este probabilitatea
sǎ fie consum anormal la unitatea
este probabilitatea
sǎ fie consum anormal la unitatea ![]()
In acest fel se obtine:

Astfel, distributia variabilei aleatoare ![]() este
este
![]()
Valoarea medie a variabilei aletoare ![]() se
calculeazǎ cu formula
se
calculeazǎ cu formula
![]()
Pentru a calcula
dispersia, folosim formula ![]()
Dar avem cǎ
![]()
deci ![]() si de
asemenea, avem imediat abaterea standard
si de
asemenea, avem imediat abaterea standard ![]()
Mediana ![]() este datǎ de
dubla inegalitate
este datǎ de
dubla inegalitate
![]()
Avem cǎ
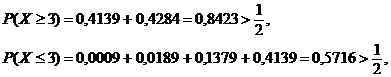
si in consecintǎ se obtine ![]()
Modul ![]() este definit ca fiind punctul de extrem local al
distributiei lui
este definit ca fiind punctul de extrem local al
distributiei lui ![]() , adic
, adic ![]() , deoArece variabila aleatoare
, deoArece variabila aleatoare ![]() ia valoarea 4 cu
probabilitatea maximǎ
ia valoarea 4 cu
probabilitatea maximǎ ![]()
21. O persoanǎ, de fiecare datǎ cand se
deplaseazǎ in orasul ![]() apeleazǎ la
serviciile unitǎtii hoteliere
apeleazǎ la
serviciile unitǎtii hoteliere ![]() . Se stie cǎ serviciile
unitǎtii
. Se stie cǎ serviciile
unitǎtii ![]() sunt
ireprosabile in 80% din cazuri. Persoana respectivǎ intentioneazǎ sǎ apeleze la serviciile unitǎtii
sunt
ireprosabile in 80% din cazuri. Persoana respectivǎ intentioneazǎ sǎ apeleze la serviciile unitǎtii ![]() panǎ cand este servit ireprosabil. Fie
panǎ cand este servit ireprosabil. Fie ![]() numǎrul de zile
cat a fost servitǎ persoana respectivǎ ireprosabil. Sǎ se scrie distributia aleatoare
numǎrul de zile
cat a fost servitǎ persoana respectivǎ ireprosabil. Sǎ se scrie distributia aleatoare ![]() , iar apoi sǎ se determine valoarea medie, dispersia,
mediana si modul variabilei aleatoare
, iar apoi sǎ se determine valoarea medie, dispersia,
mediana si modul variabilei aleatoare ![]() .
.
Solutie. Probabilitatea
ca o persoanǎ care face apel la serviciile unitǎtii ![]() sǎ fie
servitǎ ireprosabil este
sǎ fie
servitǎ ireprosabil este ![]() , iar probabilitatea ca sǎ nu fie
servitǎ in mod ireprosabil este
, iar probabilitatea ca sǎ nu fie
servitǎ in mod ireprosabil este ![]()
Deoarece ![]() este numǎrul servirilor ireprosabile panǎ la o servire nemultumitoare pentru
clientul respectiv, avem cǎ aceasta este o variabilǎ aleatoare ce
urmeazǎ legea geometricǎ. Distributia variabilei aleatoare
este numǎrul servirilor ireprosabile panǎ la o servire nemultumitoare pentru
clientul respectiv, avem cǎ aceasta este o variabilǎ aleatoare ce
urmeazǎ legea geometricǎ. Distributia variabilei aleatoare ![]() este
este
![]() sau
sau 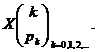
Cateva din primele probabilitǎti sunt:
![]()
Valoarea medie a
variabilei aleatoare ![]() este
este
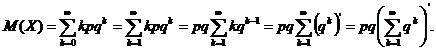
Seria care apare in
calculul valorii medii ![]() este o serie
geometricǎ, avand ratia
este o serie
geometricǎ, avand ratia ![]() , deci este convergentǎ. Prin urmare, se poate scrie
, deci este convergentǎ. Prin urmare, se poate scrie
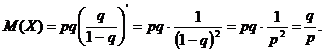
Deoarece ![]() si
si ![]() , rezultǎ cǎ
, rezultǎ cǎ ![]() . Aceasta ne spune sǎ ne asteptǎm ca o
persoanǎ sǎ fie servitǎ ireprosabil de patru ori consecutiv.
. Aceasta ne spune sǎ ne asteptǎm ca o
persoanǎ sǎ fie servitǎ ireprosabil de patru ori consecutiv.
Pentru calculul
dispersiei folosim formula ![]() Pentru aceasta,
calculǎm
Pentru aceasta,
calculǎm
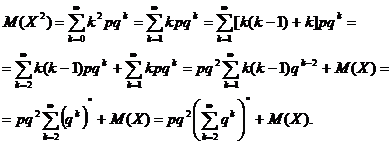
Din nou avem o serie
geometricǎ cu ratia ![]() , deci convergentǎ, drept urmare se poate scrie
, deci convergentǎ, drept urmare se poate scrie
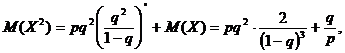
adicǎ ![]() . Astfel se ajunge la
. Astfel se ajunge la
![]()
In cazul de fatǎ, avand ![]() si
si ![]() ,se obtine
,se obtine ![]()
Mediana ![]() o determinǎm din
conditia
o determinǎm din
conditia
![]()
adicǎ ![]() va fi cel mai mic
intreg, pentru care
va fi cel mai mic
intreg, pentru care ![]() Deoarece, avem cǎ
Deoarece, avem cǎ
![]()
in conditiile
problemei va trebui sǎ calculǎm cel mai mic ![]() astfel ca
astfel ca ![]() sau
sau ![]() Astfel se obtine
Astfel se obtine ![]()
Se vede din distributia
variabilei aleatoare ![]() cǎ cea mai mare
probabilitate este 0,2, deci modul este
cǎ cea mai mare
probabilitate este 0,2, deci modul este ![]()
Timpul de ![]() de asteptare
intr-o statie de servire urmeazǎ legea exponentialǎ de parametru
de asteptare
intr-o statie de servire urmeazǎ legea exponentialǎ de parametru ![]() Sǎ se determine
valoarea medie, dispersia, abaterea medie pǎtraticǎ si mediana
pentru variabila aleatoare
Sǎ se determine
valoarea medie, dispersia, abaterea medie pǎtraticǎ si mediana
pentru variabila aleatoare ![]() .
.
Solutie.Dacǎ variabila aleatoare ![]() urmeazǎ
legea exponentialǎ de parametru
urmeazǎ
legea exponentialǎ de parametru ![]() , atunci are densitatea de probabilitate
, atunci are densitatea de probabilitate
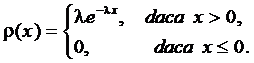
Valoarea medie se obtine din
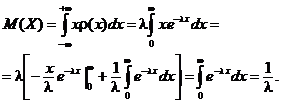
Deci timpul mediu de
asteptare in statia de servire este ![]()
Pentru dispersie
folosim formula ![]()
Dacǎ, mai jos, se integreazǎ de douǎ ori prin pǎrti, se obtine c
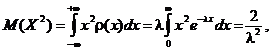
prin urmare, ![]() , iar
, iar ![]()
Pentru a determina mediana ![]() , determinǎm mai intai functia de repartitie,
anume
, determinǎm mai intai functia de repartitie,
anume ![]()
Pentru ![]() , avem
, avem ![]() , deoarece
, deoarece ![]() , cand
, cand ![]() .
.
Pentru ![]() obtinem
obtinem
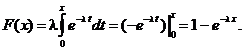
Asadar, rezultǎ cǎ
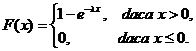
Mediana este datǎ de ecuatia ![]() , deci
, deci ![]() sau
sau ![]() , de unde
, de unde ![]()
23. Variabila aleatoare ![]() urmeazǎ legea gamma. Sǎ se calculeze
momentele initiale, iar apoi valoarea medie, disp[ersia, asimetria si
excesul variabilei aleatoare
urmeazǎ legea gamma. Sǎ se calculeze
momentele initiale, iar apoi valoarea medie, disp[ersia, asimetria si
excesul variabilei aleatoare ![]() .
.
Solutie. Dacǎ variabila
aleatoare ![]() urmeazǎ legea gamma, atuncia are densitatea de
probabilitate
urmeazǎ legea gamma, atuncia are densitatea de
probabilitate
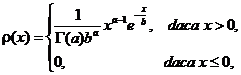
unde parametrii ![]() , iar
, iar 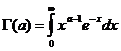 este functia lui
Euler de speta a doua.
este functia lui
Euler de speta a doua.
Pentru calculul momentelor initiale scriem
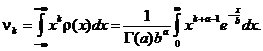
Aducem aceastǎ integralǎ la functia gamma, prin schimbarea de variabilǎ ![]() ,
, ![]() astfel rezultǎ cǎ
astfel rezultǎ cǎ
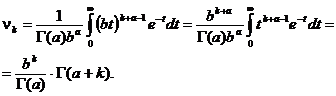
Aplicǎm formula de recurenta pentru functia gamma sia avem
![]()
Avand momentele initiale se obtin
![]()
Pentru a calcula asimetria si
excesul, trebuie sǎ calculǎm momentele centrate de ordinele 3 si 4. Dar avem cǎ momentul
centrat ![]() de ordin
de ordin ![]() , se exprimǎ cu momentele initiale prin formula
, se exprimǎ cu momentele initiale prin formula
![]()
de unde ![]() si
si ![]()
Astfel, in cazul de fatǎ, rezultǎ cǎ
![]()
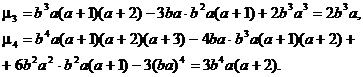
Obtinem, in acest fel,
asimetria si excesul variabilei aleatoare ![]()
24. Dacǎ ![]() este numǎrul
mǎrcilor apǎrute in trei aruncǎri cu o monedǎ, iar
este numǎrul
mǎrcilor apǎrute in trei aruncǎri cu o monedǎ, iar ![]() este numǎrul
maxim de mǎrci consecutive apǎrute in cele trei aruncǎri,
sǎ se determine coeficientul de corelatie dintre variabilele aleatoare
este numǎrul
maxim de mǎrci consecutive apǎrute in cele trei aruncǎri,
sǎ se determine coeficientul de corelatie dintre variabilele aleatoare ![]() si
si ![]() .
.
Solutie. Scriem
la inceput distributiile variabilelor aleatoare ![]() si
si ![]() , precum si a vectorului aleator
, precum si a vectorului aleator ![]()
Pentru variabila aleatoare ![]() avem distributia
de la legea binomialǎ cu
avem distributia
de la legea binomialǎ cu ![]() si
si ![]() , adicǎ
, adicǎ 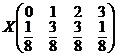 , iar prin calcul direct, se obtine distributia
variabilei aleatoare
, iar prin calcul direct, se obtine distributia
variabilei aleatoare ![]() , anume
, anume 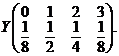
De asemenea,
distributia vectorului aleator ![]() este
este
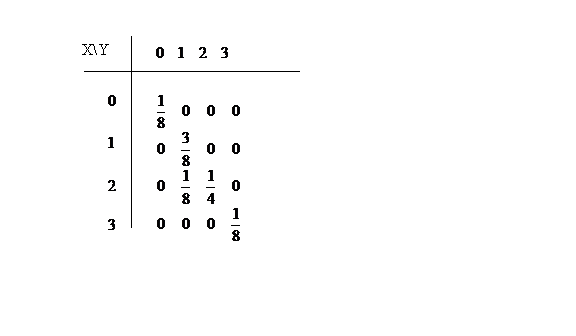
Coeficientul de corelatie il calculǎm cu formula
![]()
unde ![]() noteazǎ corelatia dintre variabilele aleatoare X si Y.
noteazǎ corelatia dintre variabilele aleatoare X si Y.
Pentru aceasta avem cǎ ![]() si in mod analog
si in mod analog ![]()
Pentru dispersie
folosim formula ![]() In primul rand avem
In primul rand avem ![]() ,deci dispersia va fi
,deci dispersia va fi ![]()
In mod analog, avem ![]() , deci
, deci ![]()
Valoarea medie a
variabilei aleatoare produs ![]() se obtine prin
se obtine prin ![]()
Prin urmare, pentru coeficientul de corelatie se obtine
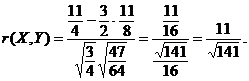
25. Variabila aleatoare ![]() urmeazǎ legea
normalǎ
urmeazǎ legea
normalǎ ![]() si fie variabial
aleatoare
si fie variabial
aleatoare ![]() Sǎ se determine
coeficientul de corelatie dintre variabilele aleatoare
Sǎ se determine
coeficientul de corelatie dintre variabilele aleatoare ![]() si
si ![]()
Solutie. Pentru a
calcula coeficientul de corelatie dintre variabilele aleatoare ![]() si
si ![]() , folosim formula
, folosim formula
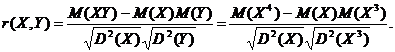
Se stie cǎ o
variabilǎ aleatoare ce urmeazǎ legea normalǎ ![]() are valoarea medie
are valoarea medie ![]() . In cazul de fatǎ
. In cazul de fatǎ ![]() , deci
, deci ![]() Prin urmare, avem
cǎ
Prin urmare, avem
cǎ ![]() , si de asemenea
, si de asemenea ![]() Asadar, se
obtine cǎ
Asadar, se
obtine cǎ
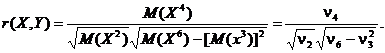
Avem nevoie de
momentele initiale ale variabilei aleatoare ![]() , motiv pentru care calculǎm toate momentele initiale. Pentru aceasta scriem
, motiv pentru care calculǎm toate momentele initiale. Pentru aceasta scriem
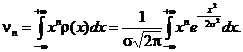
Dacǎ ![]() este impar, atunci
functia ce se integreazǎ este functie imparǎ, iar
intervalul de integrare fiind simetric fatǎ de origine, rezultǎ
cǎ integrala este zero. Prin urmare, momentele initiale de ordin
impar sunt zero, deci si
este impar, atunci
functia ce se integreazǎ este functie imparǎ, iar
intervalul de integrare fiind simetric fatǎ de origine, rezultǎ
cǎ integrala este zero. Prin urmare, momentele initiale de ordin
impar sunt zero, deci si ![]()
In cazul in care ![]() este par, adicǎ
este par, adicǎ ![]() , atunci functia ce se integreazǎ este o
functie parǎ, deci
, atunci functia ce se integreazǎ este o
functie parǎ, deci
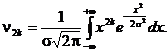
Efectuǎm schimbarea de variabilǎ datǎ prin ![]() , deci
, deci ![]() Astfel, rezultǎ
cǎ
Astfel, rezultǎ
cǎ
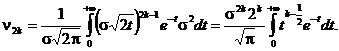
Dacǎ se are in vedere cǎ integrala la care s-a ajuns este functia gamma si dacǎ se aplicǎ in mod repetat formula de recurentǎ pentru funtia gamma, rezultǎ cǎ
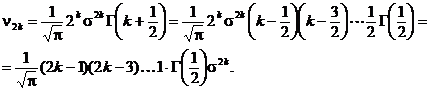
Dacǎ avem
cǎ ![]() si dacǎ
notǎm
si dacǎ
notǎm ![]() se obtine cǎ
se obtine cǎ ![]()
Prin
urmare, avem ca ![]()
![]() si
si ![]() Astfel, coeficientul de
corelatie dintre variabilele aleeatoare
Astfel, coeficientul de
corelatie dintre variabilele aleeatoare ![]() si
si ![]() este
este
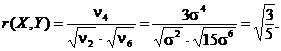
2 Folosind inegalitatea lui Cebisev, sǎ se calculeze probabilitatea ca o variabilǎ aleatoare ce urmeazǎ legea normalǎ sǎ se abatǎ de la valoarea medie:
a) mai putin de trei ori abaterea medie pǎtraticǎ,
b) mai mult de patru ori abaterea medie pǎtraticǎ.
Solitie. a)
Variabila aleatoare ![]() urmand legea normalǎ
urmand legea normalǎ ![]() , se stie cǎ
, se stie cǎ ![]() si
si ![]() , iar abaterea medie pǎtraticǎ este
, iar abaterea medie pǎtraticǎ este ![]() Prin urmare,
inegalitatea lui Cebisev devine
Prin urmare,
inegalitatea lui Cebisev devine
![]() pentru orice
pentru orice ![]()
Dacǎ se ia ![]() , rezultǎ cǎ
, rezultǎ cǎ ![]()
b) Dacǎ se
considerǎ cealaltǎ formǎ a inegalitǎtii lui
Cebisev, avem cǎ ![]() pentru orice
pentru orice ![]() care pentru
care pentru ![]() devine
devine ![]()
27. Se cunoaste cǎ o unitate de
desfacere a produselor alimentare poate deservi zilnic un numǎr de 3000
clienti, Stiind cǎ un
client care intrǎ in unitate devine cumpǎrǎtor cu probabilitatea
![]() sǎ se evalueze
probabilitatea ca
sǎ se evalueze
probabilitatea ca
a) numǎrul cumpǎrǎtorilor sǎ fie cuprins intre 1800 si 2400,
b) numǎrul cumpǎrǎtorilor sǎ fie mai mic decat 2150.
Solutie.
a)Numǎrul cumpǎrǎtorilor ![]() este o variabilǎ
aleatoare ce urmeazǎ legea binomialǎ cu parametrii
este o variabilǎ
aleatoare ce urmeazǎ legea binomialǎ cu parametrii ![]() si
si ![]() . Se cunoaste cǎ
. Se cunoaste cǎ ![]() iar
iar ![]()
Folosind inegalitatea lui Cebisev obtinem
![]() pentru orice
pentru orice ![]()
sau
![]()
Dacǎ se ia ![]() rezultǎ cǎ
rezultǎ cǎ
![]()
De asemenea, se poate folosi teorema Moivre-Laplace, adicǎ
![]()
adicǎ
![]()
![]() este
functia lui Laplace definitǎ prin
este
functia lui Laplace definitǎ prin 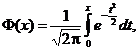 care este
tebelatǎ in Anexa I. In cazul de fatǎ de gǎseste cǎ
care este
tebelatǎ in Anexa I. In cazul de fatǎ de gǎseste cǎ 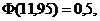 prin urmare
prin urmare ![]()
b) Folosim din nou teorema Moivre-Laplace si avem
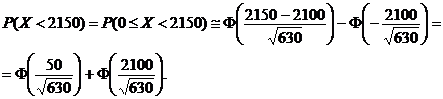
Din tabele avem cǎ
![]() iar
iar ![]()
prin urmare
![]()
28. Se iau la intamplare ![]() persoane
din populatia unui oras pentru a determina fractia
persoane
din populatia unui oras pentru a determina fractia ![]() a fumǎtorilor. Fie
a fumǎtorilor. Fie ![]() numǎrul
fumǎtorilor gǎsiti intre cele
numǎrul
fumǎtorilor gǎsiti intre cele ![]() persoane
considerate si
persoane
considerate si ![]() frecventa relativǎ a fumǎtorilor intalniti.
Sǎ se determine cat de mare trebuie sǎ fie numǎrul
frecventa relativǎ a fumǎtorilor intalniti.
Sǎ se determine cat de mare trebuie sǎ fie numǎrul ![]() al persoanelor
considerate, astfel incat
al persoanelor
considerate, astfel incat ![]() cu o
probabilitate mai mare decat 0,95. De asemenea sǎ se determine
cu o
probabilitate mai mare decat 0,95. De asemenea sǎ se determine ![]() dacǎ se stie cǎ
dacǎ se stie cǎ ![]()
Solutie. Variabila aleatoare ![]() urmeazǎ
legea binomialǎ, adicǎ are distributia
urmeazǎ
legea binomialǎ, adicǎ are distributia 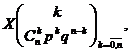
![]()
Din inegalitatea lui
Cebisev, deoarece ![]() si
si ![]() avem cǎ
avem cǎ ![]() pentru orice
pentru orice ![]() Aceastǎ
inegalitate se mai poate scrie sub forma
Aceastǎ
inegalitate se mai poate scrie sub forma
![]()
Dacǎ luǎm ![]() rezultǎ cǎ
rezultǎ cǎ
![]()
Dar se cere sǎ
calculǎm pe ![]() astfel ca aceastǎ
probabilitate sǎ fie mai mare decat 0,95, adicǎ
astfel ca aceastǎ
probabilitate sǎ fie mai mare decat 0,95, adicǎ
![]() sau
sau ![]()
Pe de altǎ
parte, avem cǎ ![]() deci il
determinǎm pe
deci il
determinǎm pe ![]() din inecuatia
din inecuatia
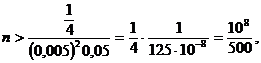
adic ![]()
Dacǎ se stie c ![]() atunci
atunci ![]() iar
iar ![]() se determinǎ din
inegalitate
se determinǎ din
inegalitate ![]() obtinandu-se
obtinandu-se ![]()
Rezultate mai bune se obtin dacǎ se foloseste teorema Moivre-Laplace.
In primul rand, avem c
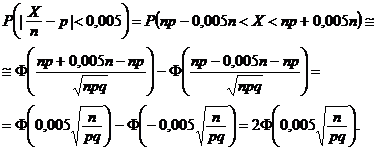
Determinǎm valoarea lui n din inegalitatea
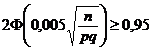 sau
sau 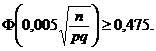
Din Anexa I se aflǎ cǎ ![]() deci avem de rezolvat inecutia
deci avem de rezolvat inecutia ![]() Dacǎ se tine seama de faptul cǎ
Dacǎ se tine seama de faptul cǎ ![]() avem cǎ
avem cǎ ![]() sau
sau ![]() de unde
de unde ![]()
Dacǎ se stie cǎ ![]() atunci avem
inecuatia
atunci avem
inecuatia![]() sau
sau ![]() adicǎ
adicǎ ![]() de unde se obtine
de unde se obtine
![]()
29. Se consider sirul ![]() de variabile aleatoare
independente douǎ
cate douǎ si care au distributiile
de variabile aleatoare
independente douǎ
cate douǎ si care au distributiile
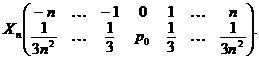
Sǎ se verifice dacǎ sirul de variabile aleatoare se supune legii numerelor mari.
Solutie. Din propriet tile unei distributii rezultǎ cǎ
![]()
De asemenea avem cǎ
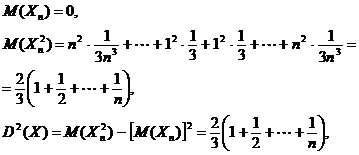
Dispersiile nefiind egal mǎrginite, nu se poate aplica teorema lui Cebisev.
Incercǎm sǎ aplicǎ teorema lui Markov. Pentru aceasta, folosind faptul cǎ variabilele aleatoare sunt independente douǎ cate douǎ, putem scrie
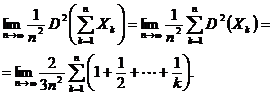
Dacǎ avem ![]() Prin urmare se poate scrie
Prin urmare se poate scrie
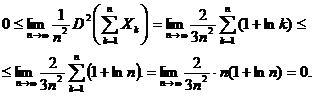
Din acest sir
de relatii rezultǎ cǎ 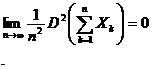 , deci conditia din teorema lui Markov este
indeplinitǎ. In consecintǎ sirul de variabile aleatoare se supune legii numerelor mari.
, deci conditia din teorema lui Markov este
indeplinitǎ. In consecintǎ sirul de variabile aleatoare se supune legii numerelor mari.
Fie
sirul de variabile aleatoare ![]() de variabile aleatoare
independente, carea au distributiile
de variabile aleatoare
independente, carea au distributiile 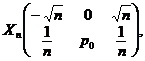 pentru
pentru ![]() iar
iar ![]() Sǎ se arate cǎ sirul de
variabile aleatoare considerat urmeazǎ legea numerelor mari.
Sǎ se arate cǎ sirul de
variabile aleatoare considerat urmeazǎ legea numerelor mari.
Solutie. Se vede
imediat cǎ ![]() Pentru dispersie avem
Pentru dispersie avem
![]()
dacǎ ![]() , iar
, iar ![]() Prin urmare
Prin urmare ![]() pentru orice
pentru orice
![]() deci dispersiile sunt
egal mǎrginite. Se poate aplica teorema lui Cebisev, drept urmare
sirul de variabile aleatoare considerat urmeazǎ legea numerelor mari,
adicǎ
deci dispersiile sunt
egal mǎrginite. Se poate aplica teorema lui Cebisev, drept urmare
sirul de variabile aleatoare considerat urmeazǎ legea numerelor mari,
adicǎ
![]() pentru orice
pentru orice ![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 45056
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved