| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Formule subiectul I bac
Distanta dintre doua puncte ![]()
mijlocul segmentului AB
este ![]()
Conditia ca trei puncte
A,B,C sa fie coliniare 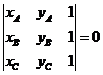
Aria triunghiului ABC ![]() unde
unde ![]()
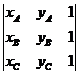
Aria triunghiului dreptunghic ![]()
Aria triunghiului echilateral
![]()
Aria triunghiului ABC
(Heron) ![]() unde
unde ![]()
Aria triunghiului ABC= ![]() =
=![]() =
=![]()
Teorema lui Pitagora b2+c2=a2
Un punct e pe o dreapta daca coordonatele lui verifica ecuatia dreptei
Perimetrul triunghiului ![]() Inaltimea
triunghiului echilateral
Inaltimea
triunghiului echilateral ![]()
Perimetrul patratului ![]() aria
patratului
aria
patratului ![]() Diagonala patratului
Diagonala patratului ![]()
Perimetrul dreptunghilui ![]() aria dreptunghiului
aria dreptunghiului ![]()
Volumul cubului ![]() aria laterala a cubului 6
aria laterala a cubului 6![]() diagonala cubului
diagonala cubului ![]()
Doua drepte d1 ;ax+by+c=0 di d2 : dx+ey+f=0 sunt
paralele daca au aceeasi panta adica ![]()
Distanta de la un punct ![]() la dreapta d:ax+by+c=0 este
la dreapta d:ax+by+c=0 este ![]()
Punctul de intersectie dintre doua drepte se determina rezovand sistemul facut de ecuatiile lor
Daca z=a+ib conjugatul lui se noteaza ![]() si e definit
si e definit ![]() =a-ib
=a-ib
Daca z=a+ib definim modulul lui ca fiind |z|=![]()
z=a+ib a se numeste parte reala si ib se numeste parte imaginara
Puterile lui i i2=-1 i3=i2 i=-i i4=1
i4k=(i4)k=1 i4k+1=i4k i=i i4k+2=i4k i2=i2=-1 i4k+3=i4k i3=i3=-i
|
x |
0 |
π/6 |
π/4 |
π/3 |
π/2 |
π |
3π/2 |
2π |
|
Sinx |
0 |
1/2 |
|
|
1 |
0 |
-1 |
0 |
|
Cos x |
1 |
|
|
1/2 |
0 |
-1 |
0 |
1 |
|
Tgx |
0 |
|
|
|
Nu exista |
0 |
Nu exista |
0 |
|
Ctgx |
Nu exista |
|
1 |
|
0 |
Nu exista |
0 |
Nu exista |
cos(2π+x)= cos x
sin(2π+x)= sin x
![]() oricare ar fi
x real
oricare ar fi
x real
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2611
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved