| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
LINII IMPORTANTE IN TRIUNGHI
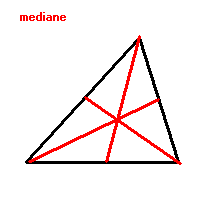
MEDIANA este segmentul care uneste un varf al triunghiului cu mijlocul laturii opuse.
-Medianele unui triunghi sunt concurente in centrul de greutate al triunghiului.
-Centrul de greutate se afla pe fiecare mediana la 2/3 de varf si 1/3 de baza, adica daca AA' este mediana in trABC si G este centrul de greutate, atunci AG=(2/3)AA'siGA'=(1/3)AA'.
-Mediana imparte un triunghi in doua triunghiuri cu aceeasi arie (echivalente).
-Centrul de greutate al unui triunghi formeaza cu vafurile triunghiului 3 triunghiuri echivalente si este singurul punct (din planul triunghiului) care are aceasta proprietate,
Intr-un triunghi dreptunghic, mediana corespunzatoare ipotenuzei este 1/2 din ipotenuza. Daca o mediana a unui triunghi este 1/2 din latura corespunzatoare ei, atunci triunghiul este dreptunghic.
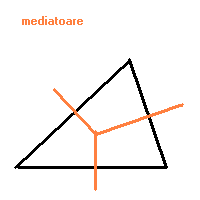
MEDIATOAREA (unui segment) este dreapta perpendiculara pe segment dusa prin mijocul segmentului.
-Mediatoarele laturilor unui triunghi sunt concurente; punctul lor de intersectie este centrul cercului cicumscris triunghiului (cercul care trece prin varfurile triunghiului).
-Orice punct de pe mediatoarea unui segment este egal departat de capetele segmentului; daca un punct este egal departat de doua puncte date, atunci el se afla pe mediatoarea segmentului determinat de cele doua puncte.
-Centrul cercului circumscris unui triunghi dreptunghic se afla la mijocul ipotenuzei. Raza acestui cerc este 1/2 din ipotenuza.
-Raza cercului circumscris unui
triunghi oarecare este ![]() ,
unde a, b, c sunt lungimile laturilor si S este aria.
,
unde a, b, c sunt lungimile laturilor si S este aria.
-Raza cercului circumscris unui
triunghi echialteral de latura a este ![]() .
.
-Intr-un tr echilateral, si numai in tr echilateral, mediatoarele laturilor sunt inaltimi, mediane si bisectoare.
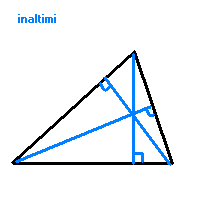
INALTIMEA este perpendi-culara dusa dintr-un varf al triunghiului pe latura opusa.
-Inaltimile unui tr. sunt concurente; punctul lor de intersectie se numeste ortocentrul triunghiului. Daca H este ortocentrul trABC, atunci A este ortocentrul trHBC, etc. Daca AA', BB' sunt inaltimi in trABC si H este intersectia lor, atunci CH AB.
-Inaltimea coresp. ipotenuzei unui tr dreptunghic este media geometrica a proiectiilor catetelor pe ipotenuza ( t. inaltimii).
-Inaltimea coresp. ipotenuzei unui tr dreptunghic este egala cu raportul dintre produsul catetelor si ipotenuza: h=(c1c2)/h.
-Inaltimea unui triunghi
echilateral de latua a este ![]() .
.
-Daca un triunghi are doua inaltimi congruente, atunci este isoscel.
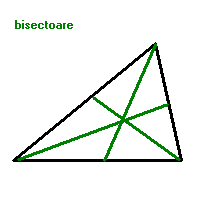
BISECTOAREA (unui unghi) este semidreapta cu originea in varful unghiului, care imparte unghiul in doua unghiuri congruente.
-Bisectoarele unui triunghi sunt concurente; punctul lor de intersectie este centrul cercului inscris in triunghi. Cercul inscris intr-un triunghi este cercul care are centrul in interiorul triunghiului si este tangent laturilor triunghiului.
-Intr-un triunghi bisectoarea oricarui unghi imparte latura opusa unghiului in segmente proportionale cu laturile unghiului. (t. bisectoarei)
-Orice punct de pe bisectoarea unui unghi este egal departat de laturile unghiului; daca un punct din interiorul unui unghi este egal departat de laturile unghiului ,atunci el se afla pe bisectoarea unghiului.
-Raza cercului inscris intr-un triunghi este egala cu S/p, unde S este aria triunghiului si p este semiperimetrul triunghiului.
-Bisectoarea exterioara a unui unghi este bisectoarea suplementului sau. Bisectoarea exterioara este perpendiculara pe bisectoarea interioara.

Teorema :
Putem avea diverse situatii in functie de latura la care se duce paralela si
pozitia acesteia fata de triunghi. Astfel, considerand cazul in care am
construit o paralala la latura BC, putem avea:
1. Paralela intersecteaza laturile AB si AC.
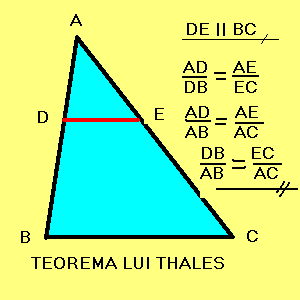
2. Paralela nu intersecteaza laturile AB si AC ci prelungiri ale acestora.
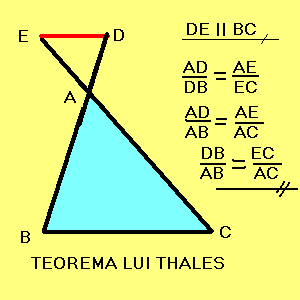
1. Paralela nu intersecteaza laturile AB si AC ci prelungirile acestora.
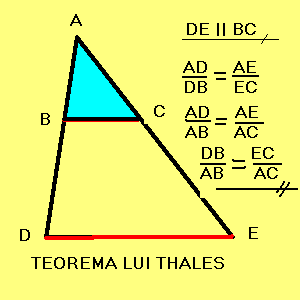
Analizand cu atentie relatiile date de teoerma lui Thales, consatam ca, de fapt, ele sunt aceleasi indiferent de pozitia dreptei construite. Faceti clic pe imaginea de mai jos pentru a avea, pe rand, toate situatiile prezentate mai sus.

Proportionalitatea segmentelor determinate de paralela pe laturile triunghiului
inseamna ca lungimile segmentelor de pe o latura se pot obtine din lungimile
segmentelor de pe cealalta latura prin inmultire cu un numar real nenul, adica:
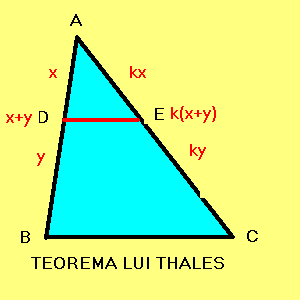
Problema rezolvata. In trABC, AB=36, AC=48, BC=60. Se considera D pe AB asa incat AD=12 si se duc dreptele: DE paralela cu BC, E pe AC, EF paralela cu AB, F pe BC, FG paralela cu AC, G pe AB, GH paralela cu BC, H pe AC, HI paralela cu AB, I pe BC si IK paralela cu AC, K pe AB. Se cere DK.
Construim figura corespunzatoare datelor problemei.
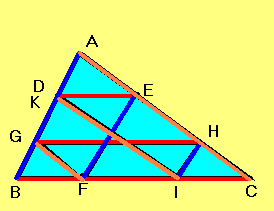
Construind figura, constatam ca punctele K si D coincid, sau
sunt foarte apropiate, deci, s-ar parea ca DK=0. Sa facem calculele pentru a
verifica acesata observatie. Pentru a nu complica inutil figura, vom scoate
separat, de fiecare data, numai elementele care ne intereseaza.
Pasul 1.
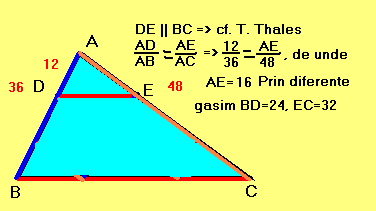
Pasul 2.
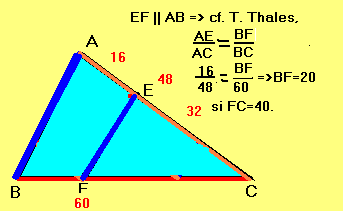
Pasul 3.
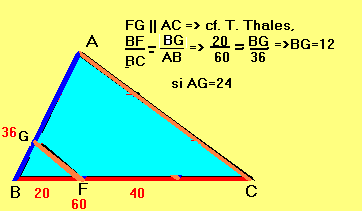
Pasul 4.
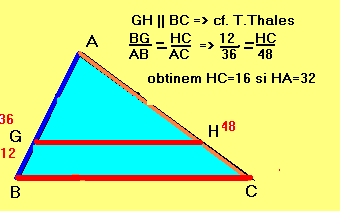
Pasul 5.
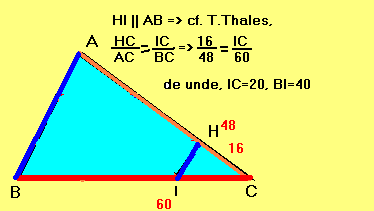
Pasul 6.
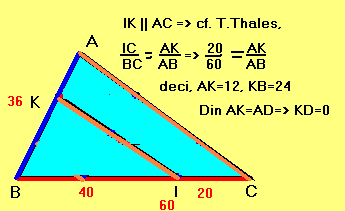
Faceti clic pe imaginea de mai jos pentru a vizualiza toate etapele

APLICATIE. Impartirea unui segment intr-un raport dat. Dandu-se un segment AB, sa se determine cu rigla (negradata) si compasul un punct M, interior segmentului, astfel incat AM/MB=k, unde k este un numar rational dat.
Vom arata cum rezolvam problema pentru k=2/3.
Din AM/MB=2/3 obtinem ca AM=2p si MB=3p. Deoarece M se afla in interorul
segmentului, obtinem ca AM=5p. Prin A ducem o dreapta oarecare pe care luam
punctele P, Q, R, S, T asa incat AP=PQ=QR=RS=ST (deci, 5 segmente congruente).
Unim T cu B si prin Q ducem o paralela la BT. Notand cu M intersectia acesteia
cu AB, conform teoremei lui Thales, avem AQ/QT=AM/MB si, cum primul raport este
2/3 rezulta ca M este punctul cautat.
Faceti clic pe imaginea de mai jos pentru a vizualiza
constructia.
Trei sau mai multe drepte paralele determina pe doua secante segmente
proportionale
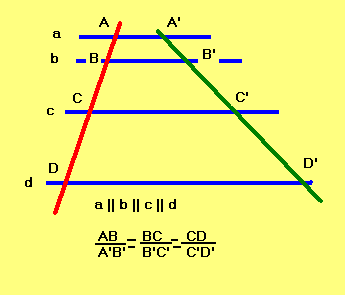
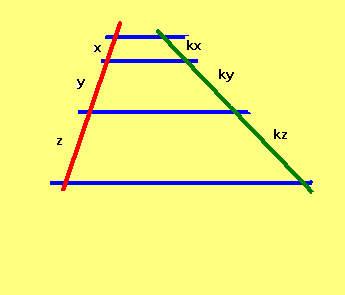
adica, masurile segmentelor de pe o secanta se afla inmultind masurile
segmentelor de pe cealalta secanta cu un numar real nenul.
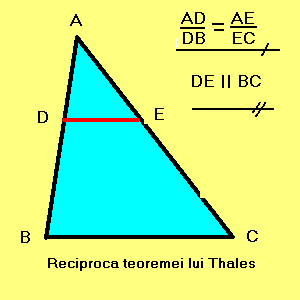
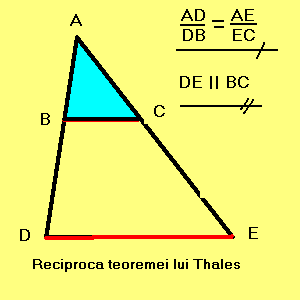
Daca o dreapta intersecteaza laturile AB si AC ale unui triunghi ABC
si determina pe acestea segmente proportionale, atunci ea este paralela cu BC.
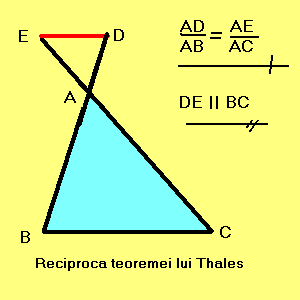
Evident ca in loc de proportia de mai sus putem avea o proportie derivata,
rezultatul ramanand acelasi.
Observatie. Afirmatia ramane adevarata si in cazul in care punctele de intersectie
sunt (ambele) pe prelungirile laturilor, dar pozitionarea lor trebuie sa fie
similara.
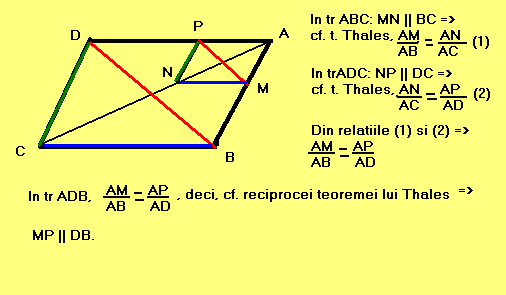
Aplicatie. Fie ABCD un paralelogram, M pe AB, N pe AC asa incat MN paralela cu BC, P pe AD asa incat NP paralela cu DC. Demonstrati ca MP este paralela cu BD.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 5079
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved