| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
APLICATII ALE TEORIEI DECIZIILOR IN VERIFICAREA IPOTEZELOR
Fie x o variabila aleatoare, functia
de repartitie F, si (x1, x2,, xn), n - selectie din x. Functia de
repartitie F este necunoscuta si se presupune ca ea apartine
unei clase P de functii de repartitie. Se considera o parte Po P si completarea sa P P Po Utilizand
o realizare (x1, x2, . xn) a n-selectiei
(X1,.Xn) trebuie sa decidem daca este rational
ca FI![]() . Este comod sa se identifice Ho cu Po si H1 cu P punand H0=,
H1=.
. Este comod sa se identifice Ho cu Po si H1 cu P punand H0=,
H1=.
Cu aceasta notatie Ho si H1 definesc o partitie a lui P. Problema revine la a alege una din aceste parti. La aceste alegeri sunt in mod normal associate decizii.
Deciziile sunt:
do daca se alege ipoteza Ho si
d1 daca se alege ipoteza H1
Exemplul 1 In controlul de calitate dintr-o intreprindere care imparte este la originea teoriei testelor, trebuie respectate anumite norme pentru reperele primite de la furnizorul sau. Fiecare piesa a unui lot poate fi clasata fara ambiguitati in piesa "buna" sau "defecta" daca ele satisfac normele sau nu. Presupunem ca putem accepta lotul daca proportia de piese defecte nu trece de un prag de toleranta po. Suntem condusi in a alege intre urmatoarele doua ipoteze si deci deciziile corespunzatoare.
![]() do - decizia de acceptare a lotului,
do - decizia de acceptare a lotului,
![]() d1 - decizia de respingere a lotului.
d1 - decizia de respingere a lotului.
In general, decizia nu va fi luata dupa un examen exhaustiv al lotului deoarece costurile de ccontrol sunt foarte mari si uneori chiar imposibil, ci numai dupa examinare unei parti. De exemplu s-a decis de a examina 100 de piese luate aleator si de a refuza lotul daca se intalnesc mai mult de 6 piese defecte si de a accepta lotul in caz contrar.
Acceptarea sau refuzul lotului este de natura aleatoare si in luarea deciziilor exista doua riscuri:
R1: Riscul de prima speta care consta in a respinge Ho cand ea este adevarata. In cazul nostru acesta este riscul vanzatorului caruia i se refuza lotul atunci cand acesta este bun.
R2: Riscul de a doua speta care consta in a accepta Ho cu julte rebuturi. In cazul nostru acesta este riscul cumparatorului care accepta un lot neconform. Aceste cazuri posibile sunt ilustrate in urmatorul tabel:
|
Ho |
H1 |
|
|
Ho |
decizie corecta |
R1 |
|
H1 |
R2 |
decizie corecta |
Ipoteze adevarate(Stari ale naturii)
Pentru intreprinderi, la fiecare tip de eroare este asociat un cost astfel ca tabloul precedent trebuie sa fie completat prin acela al costurilor.
Ipoteze adevarate
|
Ho |
H1 |
|
o |
c1 |
|
c2 |
O |
in acest exemplu, apar urmatoarele elemente:
O variabila aleatoare care ia valoarea 1 daca o piesa aleasa intamplator din lot este defecta si 0 daca nu este defecta.Notam cu p proportia de piese defecte
![]()
legea de
probabilitate a lui X este ![]() f depinde de p, notand
prin P multimea :
f depinde de p, notand
prin P multimea :
P ![]() se vede ca,
nu este niciun inconvenient de a o identifica cu multimea
se vede ca,
nu este niciun inconvenient de a o identifica cu multimea ![]()
Fie o n-selectie (x1, x2, . xn) provenita din X daca extragerea are loc "cu reluare" si o partitie a lui P in doua parti.
P ![]() care se identifica cu
care se identifica cu ![]() ,
,
P1 ![]() care se identifica
cu
care se identifica
cu ![]() ,
,
Problema este deci urmatoarea: proportia p de piese defecte fiind necunoscuta este vorba de a decide daca pIP sau daca pIP . Pentru a lua o decizie avem la dispozitie urmatoarele informatii:
realizarea (x1, x2,.,xn) a unei n-selectii (X1, X2,.Xn) provenita din X
costul riscurilor R1 si R2
eventuale informatii carene permit sa atribuim ipotezelor Ho si H1 probabilitati apriori.
Se vede ca, verificarea ipotezelor este un caz particular din teoria deciziilor. Paragraful urmator prezinta corespondenta dintre verificarea ipotezelor si teoria deciziilor.
Teoria deciziilor si verificarea ipotezelor
Tabloul de mai jos arata ca
verificarea ipotezelor este inclusa in teoria deciziilor. Pentru
simplificare vom presupune ca, clasa P este constituita din functii
de repartitie care depind de un parametru ![]() .
.
|
Teoria deciziilor |
Verificarea ipotezelor |
|
H= - stari ale naturii q: o probabilitate "apriorii" pe H X -v.a cu functia de
repartitie F(x,h), Un sir de v.a.X1,..,Xn independente din X. O selectie de dimensiune n D= o multime de decizii posibile So=[s] de strategii nealeatoare S= - strategii statistice aleatoare
|
X -
v.a cu functia de repartitie Un sir de selectii X1,..,Xn independente din X. O selectie de dimensiune n. D=; di-decizia de a accepta ipoteza Hi, Fo= teste nealeatoare O
functie f
face sa corespunda lui F= functii de decizie
aleatoare (test aleator) functia s asociaza valorii L( |
Observatia 1. Alegerea unei masuri de
probabilitate apriorii ![]() pe
pe![]() nu este necesara intotdeauna ca in teoria Neyman-Person care incearca sa
rezolve problema fara sa faca apel la acesta (
nu este necesara intotdeauna ca in teoria Neyman-Person care incearca sa
rezolve problema fara sa faca apel la acesta (![]() ). Totusi in teoria deciziilor, este de mare interes introducerea unei masuri apriorii
). Totusi in teoria deciziilor, este de mare interes introducerea unei masuri apriorii
![]() ce permite sa
definim criterii de optimizare de care se tine cont in
luarea deciziilor, aceasta inseamna ca se poseda o informatie despre
verosimilitatea relativa a ipotezelor ceea ce nu trebuie refuzata.
ce permite sa
definim criterii de optimizare de care se tine cont in
luarea deciziilor, aceasta inseamna ca se poseda o informatie despre
verosimilitatea relativa a ipotezelor ceea ce nu trebuie refuzata.
Observatia 2. Exemplul de test aleator in cazul unei partitii ![]() . Cand se considera o partitie a lui
. Cand se considera o partitie a lui ![]() formata din doua elemente H si
formata din doua elemente H si ![]() atunci D este
constituita din aceste doua elemente.
atunci D este
constituita din aceste doua elemente.
O functie ![]() se numeste functia
critica a testului aleator si k(x)
este probabilitatea ca
se numeste functia
critica a testului aleator si k(x)
este probabilitatea ca ![]() sa fie o realizare a unei n-selectii. Se poate
defini functia S cu ajutorul functiei k astfel:
sa fie o realizare a unei n-selectii. Se poate
defini functia S cu ajutorul functiei k astfel:
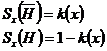
Un test aleator este deci o aplicatie S:Rn L unde L este o multime de masuri de probabilitate pe D deci ea este strategia:
![]()
Daca k nu poate sa ia
decat valorile 0 sau 1 se regaseste cazul testului nealeator in acest
caz multimea ![]() este multimea de
realizari x pentru care testul conduce la respingerea lui H; se numeste
regiune critica a testului. Se observa ca un test nealeator este
definit fara ambiguitate de regiunea sa critica.
este multimea de
realizari x pentru care testul conduce la respingerea lui H; se numeste
regiune critica a testului. Se observa ca un test nealeator este
definit fara ambiguitate de regiunea sa critica.
Observatia 3. Functia de pierdere si riscul de prima si a doua speta
Vom vedea ca pentru o functie de pierdere L particulara functia de risc introdusa in teoria deciziilor conduce in mod natural la cele doua riscuri de prima si a doua speta. in acest scop, in exemplul din observatia 2 vom lua ca functie de pierdere
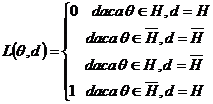
Fie S un test aleator: Functia
de risc corespunzatoare![]() cand
cand ![]() este valoarea adevarata
a parametrului. Calculam riscul pentru functia de pierdere L.
este valoarea adevarata
a parametrului. Calculam riscul pentru functia de pierdere L.
![]()
![]()
![]()
![]()
Se vede ca ![]() este probabilitatea ca
este probabilitatea ca ![]() aceasta fiind valoarea adevarata, testul S conduce
la respingerea lui H, adica riscul de prima speta; in aceiasi
maniera
aceasta fiind valoarea adevarata, testul S conduce
la respingerea lui H, adica riscul de prima speta; in aceiasi
maniera ![]() este probabilitatea
pentru ca
este probabilitatea
pentru ca ![]() aceasta fiind adevarata,
testul S conduce la acceptarea lui H; acesta este riscul de speta a doua.
aceasta fiind adevarata,
testul S conduce la acceptarea lui H; acesta este riscul de speta a doua.
In cazul unui test s nealeator![]() si
si ![]() sunt respectiv masuri
pentru masura
sunt respectiv masuri
pentru masura ![]() a multimilor K si
a multimilor K si
![]() .
.
In rezumat:
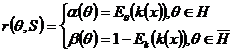
Reamintim ca se poate inzestra multimea S a testelor aleatoare care sunt functii de decizie particulare cu o relatie de preordine partiala. Testul S1 este mai puternic decat testul S2 si se scrie S1 S2 daca
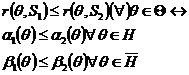
Elementele extreme ale acestei preordini definesc testele admisibile.
Decizii si strategii
Definitia 1 O problema de decizie statistica
este definita prin specificarea structurii statistice ![]() si a spatiului masurabil
si a spatiului masurabil ![]() . Probabilitatea de trecere
. Probabilitatea de trecere ![]() se numeste
strategie.
se numeste
strategie.
Spatiul ![]() se numeste spatiul
deciziilor si se presupune deci ca informatia furnizata de
se numeste spatiul
deciziilor si se presupune deci ca informatia furnizata de ![]() este cea necesara
pentru a lua o decizie din familia de decizii
este cea necesara
pentru a lua o decizie din familia de decizii ![]() , data in avans. Daca
, data in avans. Daca![]() este observatia facuta se ia o decizie
este observatia facuta se ia o decizie![]() conform legii de probabilitate
conform legii de probabilitate![]() pe (D,D); in particular daca
pe (D,D); in particular daca![]() este pentru toti
este pentru toti ![]() o masura
Dirac in punctul
o masura
Dirac in punctul ![]() a lui
a lui![]() se spune ca strategia este determinista. Ea consta
in a lua decizia
se spune ca strategia este determinista. Ea consta
in a lua decizia![]() , dupa ce s-a observat
, dupa ce s-a observat![]() . Din punct de vedere matematic, este usor sa intelegem
de ce nu ne putem limita numai la considerarea strategiilor deterministe.
Familia strategiilor este o multime convexa in timp ce familie
strategiilor deterministe nu este.
. Din punct de vedere matematic, este usor sa intelegem
de ce nu ne putem limita numai la considerarea strategiilor deterministe.
Familia strategiilor este o multime convexa in timp ce familie
strategiilor deterministe nu este.
Exemplul 1. Presupunem ca avem o productie de serie omogena a unui acelasi obiect, se prelucreaza n-obiecte fabricate pentru control: poate sa se decida statistic, cunoscand numarul de obiecte defecte din cele n-controlate, daca productia in ansamblul sau poate fi acceptata sau nu. O ipoteza relativa la modul de extragere este usor de a vedea ca structura statistica este definita de:
![]() iar
iar ![]() si K este o
algebra de parti. Spatiul deciziilor este format din doua
puncte care corespund la acceptarea sau neacceptarea productiei
globale. Intuitiv teoria din capitolul urmator ne arata ca este
de tipul: este fixat un nivel de admisibilitate
si K este o
algebra de parti. Spatiul deciziilor este format din doua
puncte care corespund la acceptarea sau neacceptarea productiei
globale. Intuitiv teoria din capitolul urmator ne arata ca este
de tipul: este fixat un nivel de admisibilitate![]() . Daca
. Daca![]() se accepta productia, dacaa
se accepta productia, dacaa![]() se respinge productia. Din punct de vedere practic, notiunea
de strategie stocastica poate sa para ireala, exemplu de
mai sus arata ca, in anumite cazuri
se respinge productia. Din punct de vedere practic, notiunea
de strategie stocastica poate sa para ireala, exemplu de
mai sus arata ca, in anumite cazuri ![]() aproape de
aproape de ![]() este dificil sa se ia o decizie. Repartitia de
probabilitate
este dificil sa se ia o decizie. Repartitia de
probabilitate ![]() definita pentru
orice
definita pentru
orice ![]() de strategie S poate
fi interpretata practic ca un fel de preferinta pe multimea
deciziilor posibile.
de strategie S poate
fi interpretata practic ca un fel de preferinta pe multimea
deciziilor posibile.
Este dificil de a da un sens concret ![]() -algebrei D a carui utilitate este numai
matematica. Astfel pentru anumite probleme de decizie se considera
numai multimea de decizii.
-algebrei D a carui utilitate este numai
matematica. Astfel pentru anumite probleme de decizie se considera
numai multimea de decizii.
in multe cazuri, se cunoaste o multime
![]() care apartine lui T D care corespunde la o multime de
decizii corecte (juste): adica daca
care apartine lui T D care corespunde la o multime de
decizii corecte (juste): adica daca![]() este valoarea adevarata a parametrului, decizia
este valoarea adevarata a parametrului, decizia ![]() luata este compatibila cu
luata este compatibila cu![]() daca cuplul
daca cuplul ![]() . in exemplul de mai sus, se presupune ca productia
este acceptabila daca proportia de obiecte defecte este
inferioara lui p0 un numar real dat. Daca se noteaza
. in exemplul de mai sus, se presupune ca productia
este acceptabila daca proportia de obiecte defecte este
inferioara lui p0 un numar real dat. Daca se noteaza![]() unde 0 reprezinta acceptarea productiei si 1
respingerea sa avem:
unde 0 reprezinta acceptarea productiei si 1
respingerea sa avem:
![]()
Definitia 1. Probabilitatea
de trecere IS compusa din ![]() si S astfel
si S astfel ![]() se numeste imaginea
(puterea strategiei) S. in particular daca strategia este determinista
sau, atunci
se numeste imaginea
(puterea strategiei) S. in particular daca strategia este determinista
sau, atunci ![]() .
.
Imaginea strategiei S pentru orice ![]() , este o repartitie de probabilitate a statisticii s cu
valori in
, este o repartitie de probabilitate a statisticii s cu
valori in ![]() si nu este a lui
S ca statistica.
si nu este a lui
S ca statistica.
Studiul unei strategii se face in statistica matematica esential cu ajutorul imaginii sale, ceea ce inseamna eficienta practica a unei strategii este definita de imaginea sa.
Aplicatii ale teoriei deciziilor statistice in verificarea ipotezelor statistice
Teoria verificarii ipotezelor statistice este un caz particular al teoriei deciziilor statistice. In orice problema de statistica este vorba de a extrage din observatiile obtinute, reprezentate printr-un punct, informatii despre valoarea unui parametru q
O problema de decizie se compune din elementele:
a) (H, T)
- spatiul starilor, T este o ![]() - algebra de parti a lui H, si elementele
lui H, si elementele lui H se numesc stari.
- algebra de parti a lui H, si elementele
lui H, si elementele lui H se numesc stari.
b)
Probabilitatea apriorii ![]() ,
,
c) ![]() - o variabila aleatoare cu valori in spatiul X,
care va fi definita prin functia de repartitie Ph.
- o variabila aleatoare cu valori in spatiul X,
care va fi definita prin functia de repartitie Ph. ![]() un sir de
variabile aleatoare independente fiecare au aceeiasi repartitie ca
un sir de
variabile aleatoare independente fiecare au aceeiasi repartitie ca ![]() . Primele n din acest sir, formeaza o n-selectie
si este fixata inainte de experienta. Se pot considera
cazuri cand experimentarea se continua sau se opreste in functie
de rezultatul obtinut.
. Primele n din acest sir, formeaza o n-selectie
si este fixata inainte de experienta. Se pot considera
cazuri cand experimentarea se continua sau se opreste in functie
de rezultatul obtinut.
Remarcam
ca, legea de probabilitate a n selectiei depinde in mod egal de h, fara
a face confuzie cu legea de probabilitate a lui ![]() .
.
d) O selectie de volum n.
e) D o multime
de elemente ![]() numite decizii.
numite decizii.
f) ![]() - multime de strategii (functii de decizie) care
asociaza oricarui rezultat al selectiei o decizie
- multime de strategii (functii de decizie) care
asociaza oricarui rezultat al selectiei o decizie ![]() . Astfel de strategii se numesc pure sau nealeatoare.
. Astfel de strategii se numesc pure sau nealeatoare.
g)
Consideram pe D inzestrat cu o![]() -algebra si
-algebra si ![]() probabilitatea de
trecere} se numeste multimea de strategii mixte (functii de
decizii mixte) sau aleatoare.
probabilitatea de
trecere} se numeste multimea de strategii mixte (functii de
decizii mixte) sau aleatoare.
h) ![]() - functia de pierdere, unde L(h,d) reprezinta
pierderea suferita cand h este starea realizata si d decizia
luata. Aceasta functie include toate costurile luate in calcul, in
particular costurile de experimentare.
- functia de pierdere, unde L(h,d) reprezinta
pierderea suferita cand h este starea realizata si d decizia
luata. Aceasta functie include toate costurile luate in calcul, in
particular costurile de experimentare.
a) presupunand ca h si d
sunt alese de mecanisme aleatoare se poate considera L o variabila
aleatoare fapt ce va permite definirea functiei de risc. Studiu
strategiilor in statistica matematica se realizeaza cu ajutorul
puterii caracteristice (sau imagini) ![]() .
.
Particularizarile problemei de decizie la verificarea problemei de decizie sunt:
a') Spatiul
starilor H devine spatiul parametrilor ![]() vor fi numite ipoteze
si notate in multe carti cu H cu indice.
vor fi numite ipoteze
si notate in multe carti cu H cu indice.
e') Spatiul
deciziilor D=
deci D este in corespondenta bijectiva cu partitia ![]() a lui
a lui ![]() .
.
f') ![]() functia de decizie nealeatoare acum numita test nealeator asociaza fiecarui rezultat x un element al
partitiei
functia de decizie nealeatoare acum numita test nealeator asociaza fiecarui rezultat x un element al
partitiei ![]() .
. ![]() - strategiei aleatoare ii corespunde un test aleatoriu
asociaza lui x o probabilitate pe D. Celelalte elemente care intervin intr-o
problema de decizie intervin si in problemele de verificare a
ipotezelor statistice.
- strategiei aleatoare ii corespunde un test aleatoriu
asociaza lui x o probabilitate pe D. Celelalte elemente care intervin intr-o
problema de decizie intervin si in problemele de verificare a
ipotezelor statistice.
Definitia
1. Se numeste criteriu orice statistica![]() .
.
Fie ![]() si
si ![]() doua ipoteze
disjuncte.
doua ipoteze
disjuncte.
Definitia 2 Criteriul
obtinut din strategia![]() atribuind ipotezelor
atribuind ipotezelor ![]() si
si ![]() probabilitatile
probabilitatile
![]() si
si ![]() se numeste criteriu
de verificare a ipotezei
se numeste criteriu
de verificare a ipotezei ![]() cu alternativa
cu alternativa ![]() . Functia de putere a lui
. Functia de putere a lui ![]() este restrictia
pe
este restrictia
pe ![]() a imaginii
a imaginii ![]() .
.
![]() a
criteriilor
a
criteriilor ![]() .
.
Definitia 3. Spunem
ca doua criterii ![]() si
si ![]() de verificare a ipotezei
de verificare a ipotezei ![]() cu alternativa
cu alternativa ![]() sunt echivalente daca
au aceeiasi functie de putere.
sunt echivalente daca
au aceeiasi functie de putere.
Decizii incorecte se pot lua numai in doua cazuri:
i)
sa
alegem alternativa ![]() in timp ce
in timp ce ![]() , acestui eveniment ii corespunde probabilitatea
, acestui eveniment ii corespunde probabilitatea ![]() .
.
ii) sa
luam decizia ![]() cand in realitate
cand in realitate
![]() si acestui eveniment ii corespunde probabilitatea
si acestui eveniment ii corespunde probabilitatea ![]()
![]() .
.
Definitia 4. Daca![]() este un criteriu de verificare a ipotezei
este un criteriu de verificare a ipotezei ![]() cu alternativa
cu alternativa ![]() , atunci numarul
, atunci numarul ![]() se numeste nivel de semnificatie
se numeste nivel de semnificatie
Criteriul ![]() se numeste nedeplasat daca
se numeste nedeplasat daca ![]() .
.
Multimea
![]() se numeste domeniu
critic.
se numeste domeniu
critic.
Relatii de preordine in multimea testelor
Problema esentiala in verificarea ipotezelor este de a gasi un cel mai bun test (criteriu) de verificare a unei ipoteze in raport cu alternativa sa; daca astfel de criteriu axista.
Definitia 2.1.
Fie doua criterii ![]() si
si ![]() de verificare a ipotezei
de verificare a ipotezei ![]() cu alternativa
cu alternativa ![]() . Punem
. Punem
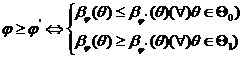 si
si
![]() daca cel putin un
daca cel putin un ![]() avem o inegalitate stricta. Citim pe
avem o inegalitate stricta. Citim pe ![]() (
(![]() este mai puternic decat
este mai puternic decat ![]() ).
).
Desigur relatia de preordine data este de o functie de pierdere sau de o probabilitate apriori introduse in doua straturi sunt valabile si in clasa strategiilor corespunzatoare criteriilor.
Riscul ![]() corespunzator criteriului de verificare a ipotezei
corespunzator criteriului de verificare a ipotezei ![]() cu alternativa
cu alternativa ![]() are forma:
are forma:
![]()
![]() ,
, ![]()
Definitia 2.2 Criteriul ![]() este preferat criteriului
este preferat criteriului ![]() si notam
si notam ![]() daca
daca ![]()
Definitia 2. Criteriul ![]() se numeste admisibil daca nu exista un alt
criteriu
se numeste admisibil daca nu exista un alt
criteriu ![]() astfel ca sa fie
preferat lui
astfel ca sa fie
preferat lui ![]() .
.
Teorema 1. ![]()
![]() .
.
Demonstratie.
Fie ![]() ,
, ![]() tinand cont de definitia lui L atunci
tinand cont de definitia lui L atunci ![]() deci
deci ![]() .
.
3. Criterii optime
Definitia 3.1 Criteriul
![]() de verificare a ipotezei
de verificare a ipotezei ![]() cu alternativa
cu alternativa ![]() se numeste uniform cel mai puternic (UCMP)
daca pentru orice alt criteriu
se numeste uniform cel mai puternic (UCMP)
daca pentru orice alt criteriu
![]() de verificare a ipotezei
de verificare a ipotezei ![]() cu alternativa
cu alternativa ![]() este adevarata relatia:
este adevarata relatia:
![]() .
.
Teorema 2 Fie
![]() si
si ![]() un criteriu de verificare a ipotezei
un criteriu de verificare a ipotezei ![]() cu alternativa
cu alternativa ![]() cu nivelul de semnificatie
cu nivelul de semnificatie ![]() . Daca
. Daca![]() este UCMP de verificare a ipotezei
este UCMP de verificare a ipotezei ![]() cu alternativa
cu alternativa ![]() cu nivelul de semnificatie
cu nivelul de semnificatie ![]() atunci
atunci ![]() este testul UCMP de
verificare a ipotezei
este testul UCMP de
verificare a ipotezei ![]() cu alternativa
cu alternativa ![]() .
.
Demonstratie
daca![]() este un criteriu de verificare a ipotezei
este un criteriu de verificare a ipotezei ![]() cu alternativa
cu alternativa ![]() astfel ca
astfel ca ![]() atunci
atunci ![]()
in
virtutea proprietatii UCMP in raport cu ![]() rezulta
rezulta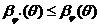
![]() .
.
Corolar.
Criteriul ![]() de verificarea
ipotezei
de verificarea
ipotezei ![]() cu alternativa
cu alternativa ![]() este UCMP daca si
numai daca este UCMP in raport cu orice
este UCMP daca si
numai daca este UCMP in raport cu orice ![]() .
.
Teorema 3 Fie ![]() L, Q o
probabilitate apriori pe
L, Q o
probabilitate apriori pe ![]() si presupunem
finite integralele
si presupunem
finite integralele ![]()
![]() atunci exista un
criteriu nealeator
atunci exista un
criteriu nealeator ![]() numit optim
Bayesian, adica
numit optim
Bayesian, adica![]()
![]() criteriu de verificare a ipotezei
criteriu de verificare a ipotezei ![]() cu alternativa
cu alternativa ![]() .
.
Demonstratie. Consideram ![]() unde
unde ![]() este un criteriu
arbitrar. Din lema lui Neumane-Pearson a s rezulta ca multimea
D este convexa si inchisa si functia liniara
este un criteriu
arbitrar. Din lema lui Neumane-Pearson a s rezulta ca multimea
D este convexa si inchisa si functia liniara![]() isi atinge maximul intr-un punct extrem a lui D deci
rezulta ca, testul este nealeator.
isi atinge maximul intr-un punct extrem a lui D deci
rezulta ca, testul este nealeator.
Urmatoarea (problema) teorema rezolva unei ipoteze simple cu alternativa simpla si cu nivel de semnificatie dat.
Teorema
4. Fie P0 si P1 doua
masuri de probabilitate diferite pe (X,K) cu densitatile p0
si p1 in raport cu o masura![]() . Pentru orice constanta nenegativa
. Pentru orice constanta nenegativa![]() criteriul
criteriul ![]() de forma:
de forma:
![]()
![]()
este UCMP pentru verificarea ipotezei P
cu alternativa P .
Pentru orice ![]() exista un
criteriu
exista un
criteriu ![]() cu nivel de semnificatie
cu nivel de semnificatie
![]() .
.
Demonstratie.
Existenta criteriului ![]() este asigurata de
lema NP. Fie functia
este asigurata de
lema NP. Fie functia
![]() ,
, ![]() .
.
Atunci ![]() este crescatoare si
continua numai unul din cazuri
este crescatoare si
continua numai unul din cazuri
a) daca![]() atunci orice criteriu
atunci orice criteriu ![]() pentru care
pentru care ![]() daca
daca![]() si
si ![]() daca
daca![]() este UCMP.
este UCMP.
b) Daca![]() atunci criteriul
atunci criteriul
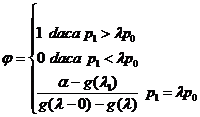
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2205
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved