Matematica distractiva

Poate fi matematica si distractiva ? Orice domeniu, cat de riguros, are si aspecte mai putin formale - iar matematica nu este din fericire o exceptie. Bineinteles ca fanii generatiilor PRO nu vor gasi nimic distractiv in cele expuse in continuare - dar la urma urmei nu este vina mea personala. Si nici a matematicii, fireste.

Matematica, asa cum se preda ea in scoala, este din pacate prea putin atractiva. Manualele au saracit in ultimii ani din cauza restructurarii programelor scolare, care au acordat o atentie sporita disciplinelor 'umaniste' (orice absolvent de liceu sustine doua examene la romana, in vreme ce exista multe profiluri la care matematica a fost deplin abolita din examenul de bac). Si asa, din manualele vechi si noi se pot invata in primul rand sabloane de rezolvare a unor exercitii mai mult sau mai putin raspandite. Inveti astazi sa calculezi integrale rational-trigonometrice si ai surpriza sa constati ca la examene se dau rational-exponentiale, pentru ca asa le-a fost mai comod profesorilor care au alcatuit subiectele. Si de altfel, prea multi invata matematica (daca o fac), doar de frica examenelor. Oare sa nu aiba aceasta materie nimic care sa merite timpul pierdut cu studiul ?

Atractivitatea unei expuneri are un rol hotaritor pentru impactul materialului expus asupra auditoriului. Daca v-as spune ca un an are 31.536.000 de secunde, ati uita acel numar imens imediat dupa ce ati inchide pagina de fata. Altfel ati retine insa ca secunde reprezinta un nano-secol, cu o aproximatie de 1%.

Cred ca un absolvent de liceu trebuie in primul rand sa ramana cu abilitatea de a gandi, de a elabora rationamente - si abia apoi cu insusirea unor algoritmi de calcul. Dezvoltarea acestei abilitati presupune :

1. reorganizarea programelor si manualelor scolare;
2. eliminarea rigiditatii expunerii.

In seria curenta de pagini, voi introduce cateva exemple menite tocmai a spori atractivitatea prezentarii matematicii.

Exemplul 1. Imediat dupa predarea regulii de trei simple in clasa a VI^a, ar trebui propusa elevilor urmatoarea :

O orchestra compusa din 40 de instrumentisti interpreteaza o melodie in 4 minute. In cat timp va fi interpretata melodia de o orchestra compusa din 80 de instrumentisti ?

Dincolo de raspunsul pe care il intuiti (evident, tot in 4 minute), este important sa subliniem caracterul nociv al problemelor-sablon cu muncitori sapand la santuri sau cu conducte care umplu rezervoare, prezente in mai toate manualele. Trebuie ca de fiecare data cand este predat un astfel de sablon sa se insiste si asupra situatiilor in care el se aplica. Astfel, se va evita ca instrumentistii din problema noastra sa fie asimilati muncitorilor care sapa transee.

Exemplul al 2-lea. Acest exemplu celebru dateaza din antichitate. Filozoful Zenon si-a pus urmatoarea problema :

Ahile alearga in aceeasi directie si in acelasi sens cu o broasca testoasa, care are un avans d . Ahile are insa o viteza de 10 ori mai mare decat cea a broastei testoase. Cand Ahile va ajunge in punctul unde initial se afla broasca, aceasta va mai fi parcurs inca d/10 ; cand Ahile va ajunge si in acest punct, broasca tot va mai avea un avans d/100 . Continuand rationamentul la infinit, putem trage concluzia ca Ahile nu va ajunge niciodata broasca, ceea ce este paradoxal. Explicati situatia.

Explicatia (cel putin cea la care m-am gandit eu) este ca, in ciuda faptului ca pare infinita, suma :
d + d/10 + d/100 + . . .
are in fapt o valoare finita, care reprezinta chiar distanta dupa care Ahile depaseste broasca. Sa gandim problema si sub aspectul coordonatei timp . Fie t durata dupa care Ahile al nostru reuseste sa ajunga unde se afla initial broasca. Intre timp, aceasta nu a stat degeaba si a luat un usor avans, pe care eroul il remonteaza dupa t/10 s.a.m.d. . Suma :
t + t/10 + t/100 + . . . = 10t/9
reprezinta chiar durata dupa care broscuta va fi intrecuta. Mai interesante par insa speculatiile referitoare la continuitatea timpului care se pot face pornind de aici. Are timpul o scurgere continua (modelata de exemplu de multimea numerelor reale pozitive, care intre oricare doua numere reale aseaza cel putin un altul) sau este o succesiune de intervale discrete de durata foarte mica dar bine stabilita ? Materia, dupa cum se stie, are o structura discreta - fiind compusa din numere intregi de particule de mase bine stabilite. Grosier, se poate afirma ca masa oricarui corp este un multiplu al unitatii atomice de masa, definita ca 1/12 din masa atomului de carbon 12. Situatia de mai sus pare sa fie o dovada in sprijinul continuitatii timpului - daca orice durata ar fi multiplu al unei unitati t₀ , atunci nu s-ar putea face o diviziune a unui interval in oricate parti, ceea ce sus se face de altfel. Un timp continuu ne permite in schimb sa afirmam ca exista momentele t, t/10, t/100, . . . t/10ⁿ oricare ar fi n natural.

Exemplul al 3-lea. Construiti patru triunghiuri echilaterale cu ajutorul a sase bete de chibrit.

Lasand la o parte faptul ca in cutiile de chibrituri fabricate in Romania nu se pot gasi bete de lungimi egale - deci sub aspect practic problema este imposibila - ceea ce se urmareste aici este tot demontarea fixatiilor de tip sablonard existente in multe minti. Exemplul de mai sus a fost luat din cartea 'Din spectacolul matematicii', scrisa de Gh. Paun si aparuta in 1983 la Ed. Albatros. Cei care au vazut probleme cu chibrituri (din pacate, revistele actuale nu prea mai contin teste de logica, fiind mai ocupate cu barfe si can-can-uri - chestiuni mult gustate de public. Nici nu e de mirare ca interesul pentru invatamant si cultura se duce de rapa. Mass-media este primul rau care il distruge.) - asa, ziceam de cei ce si-au mai batut capetele cu probleme cu chibrituri - le-au intins pe masa si le-au rasucit pana ce figura a iesit cum cerea problema. Asta era sablonul care aici nu se poate aplica - oricum ati rasuci sase bete de chibrit pe masa, nu vor iesi mai mult de trei triunghiuri. Solutia este sa construiti un tetraedru regulat . Nu-i asa ca e minunata mintea umana ?

Exemplul al 4-lea. Se dau doua segmente de dreapta, de lungimi a si 3a . Care dintre ele contine mai multe puncte ?

Raspunsul la aceasta problema poate parea socant : niciunul . Dispunem segmentele paralel unul cu celalalt, cu cel mic AB deasupra celui mare CD , cu o distanta oarecare intre ele (puteam sa nu le dispunem paralel). Fie I punctul de intersectie dintre dreptele AD si BC (laturile neparalele ale trapezului ABCD , nu diagonalele sale !). Unind I cu un punct arbitrar M de pe CD , vom gasi pentru fiecare pozitie a lui M un punct de interesectie N intre IM si AB . Aceasta inseamna nic mai mult nici mai putin decat ca nu sunt pe CD mai multe puncte decat pe AB . Vezi si figura alaturata :

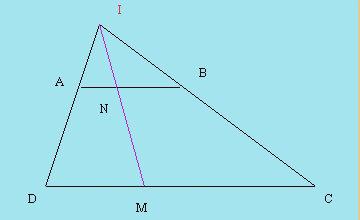
Pentru cunoscatori, rezultatul problemei se exprima simplist astfel : 3 * = .

Exemplul al 5-lea. Intr-o clasa sunt 36 de elevi. Care este probabilitatea ca (cel putin) doi dintre ei sa-si serbeze ziua de nastere in aceeasi zi a anului ?

Presupunem ca anul are 365 de zile (dupa cum bine stiti, exista si ani cu 366 de zile). Eroarea comisa nu este prea mare, deci ne permitem sa facem o astfel de aproximare. Ne gandim care ar fi probabilitatea evenimentului contrar : sa nu existe doi elevi nascuti in aceeasi zi a anului. Dupa care, vom obtine rezultatul dorit scazand din 1 probabilitatea evenimentului contrar.

Primul elev poate fi nascut in orice zi a anului. Cel de-al doilea poate fi nascut in orice zi, mai putin cea in care este nascut primul (observati, am introdus o ordonare a multimii elevilor), deci are 364 de sanse din 365 sa nu fie nascut in aceeasi zi cu primul. Al treilea va avea 363 de posibilitati din 365 sa nu fie nascut in aceeasi zi cu vreunul din primii doi, . . ., pana cand al 36-lea va ramane cu 330 de posibilitati dintr-un total de 365. Probabilitatea ca sa nu fie doi nascuti in aceeasi zi va fi deci produsul tuturor acestor probabilitati :

Prin urmare, probabilitatea ca sa existe cel putin doi elevi din 36 cu aceeasi zi de nastere va fi q = 1 - p . Calculand efectiv, gasim o valoare de aproximativ 71%. Sincer sa fiu, nu ma asteptam la o valoare atat de mare inainte sa ma apuc sa rezolv efectiv problema.

Exemplul al 6-lea. Sa examinam figura de mai jos.

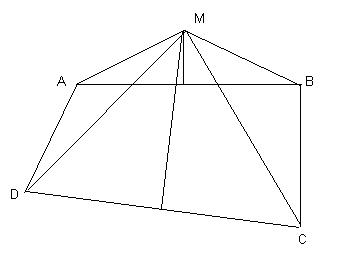
Pe segmentul [AB] construim unghiul obtuz BAD si unghiul drept ABC. Punctele C si D le alegem astfel incat AD = BC. Mediatoarele segmentelor [AB] si [CD] se taie in M. Dupa cum se observa, triunghiurile MAB si MCD formate sunt isoscele; rezulta congruenta (cazul LLL) pentru triunghiurile MAD si MBC. Deci, unghiurile MAD si MBC sunt congruente; scazand din acestea unghiurile congruente MAB, respectiv MBA, ramane ca unghiurile BAD si ABC sunt congruente. Adica un unghi obtuz este congruent cu unul drept !!! Explicati unde este greseala.

Geometria este (uneori) 'arta de a rationa corect chiar si pe figuri gresite'. In alte cazuri insa, de executia corecta a figurii depinde desfasurarea intregului rationament. Este si cazul de fata. Pe o figura corecta (pe care va indemnam sa o executati singuri), se poate observa ca 'unghiul' MAD capata o deschidere mai mare de 180 de grade, deci nu mai este un unghi in sensul definitiei. Ca atare, chiar daca triunghiurile MAD si MBC raman congruente, din aceasta congruenta nu mai deducem ca un unghi obtuz ar fi egal cu unul drept.

Exemplul al 7-lea. Pe situl www.clopotel.ro am gasit imaginea de mai jos.

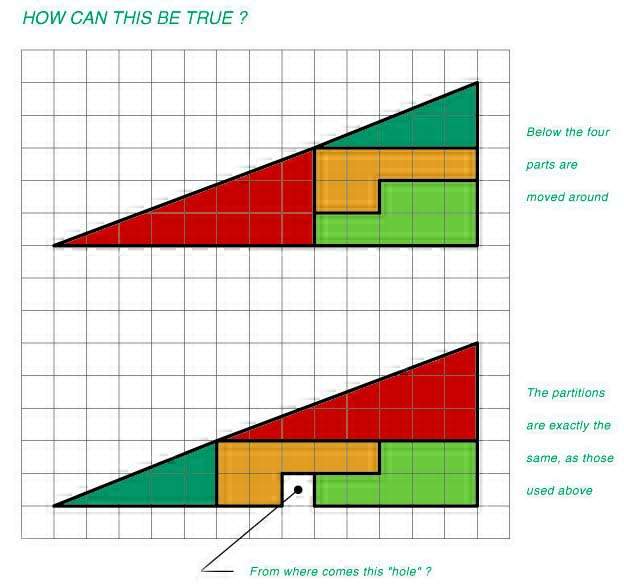
Cum este posibil ca doar schimband pozitia triunghiului rosu cu cel verde, sa apara 'gaura' din figura de jos ?

Caroiajul este elementul esential al figurii. Daca privim cu atentie, observam ca triunghiul rosu are catetele de 8 si 3, cel verde are catetele de 5 si 2, iar triunghiul mare are catetele de 13 si 5. Evident, cele trei triunghiuri nu sunt (cum se doreste sa se creeze impresia) asemenea. In consecinta, in jurul varfului comun triunghiurilor rosu si verde, suma unghiurilor nu este 180 de grade. In prima figura, suma unghiurilor din acel punct este de 90 + + , unde tg() = 2/5 si tg() = 8/3. Calculand tg( + ), gasim valoarea (-46), ceea ce inseamna ca suma celor doua unghiuri este un unghi obtuz. Inca o data, corectitudinea figurii se dovedeste esentiala in efectuarea unui rationament corect.

Pe o figura corecta, se poate observa ca (mentinand impartirea in raport 2/3 a catetei mici), pe cateta mare vor aparea segmente cu lungimea de 5.2, respectiv 7.8 si nu de 5 si 8.