Extremele functiilor de mai multe variabile

Extremele functiilor de mai multe variabile

Definitia 1. Un punct se numeste punct de maxim local (respectiv de minim local) al functiei , daca exista o vecinatate a lui astfel incat, pentru orice sa avem (respectiv ).

Aceste puncte se numesc puncte de extrem (local) ale functiei. Valoarea a functiei intr-un punct de maxim (minim) local se numeste maximul (minimul) local al functiei. Vom nota prin , interiorul multimii .

Propozitia 1. Daca functia are derivate partiale intr-un punct de extrem atunci derivatele partiale se anuleaza in acest punct, , .

Definitia 2. Un punct se numeste punct stationar al functiei daca functia este diferentiabila in si daca diferentiala sa este nula in acest punct, .

Dar .

Asadar, este un punct stationar (critic) al functiei cand functia este diferentiabila in punctul si are derivatele partiale nule in acest punct.

Propozitia 2. Orice punct de extrem local din interiorul multimii in care functia este diferentiabila este punct stationar al functiei. Reciproca nu este adevarata.

Punctele stationare ale functiei care nu sunt puncte de extrem ale sale se numesc puncte sa ale lui .

Interpretare geometrica Graficul functiei este o suprafata a carei ecuatie este si are in punctul sa un plan tangent, a carui ecuatie este

Daca este punct stationar (), planul tangent este paralel cu planul . In concluzie daca este diferentiabila pe o multime deschisa , punctele stationare ale lui sunt toate solutiile ale sistemului:

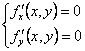
Cum orice punct de extrem local este punct stationar, rezulta ca punctele de extrem local se afla printre solutiile sistemului de mai sus (dar nu toate solutiile sistemului sunt puncte de extrem).

Ca si la functii de o singura variabila unde pentru a identifica un punct de extrem analizam semnul derivatei a doua in acel punct, pentru a identifica printre punctele stationare unele puncte de extrem (dar nu neaparat toate punctele de extrem) va trebui sa recurgem la derivatele partiale de ordinul doi.

Teorema. Daca este un punct stationar al functiei si daca are derivate partiale de ordinul doi continue intr-o vecinatate a lui , atunci

Daca , atunci este un punct de extrem local al functiei si anume:

daca ,    este un punct de minim;

daca ,    este un punct de maxim.

Daca ,    atunci nu este un punct de extrem al functiei .

Fie , este un punct de minim (maxim) local daca (). Daca este un punct stationar atunci , .

Punctul este stationar daca este diferentiabila in si daca si se obtine din rezolvarea sistemului derivatelor partiale.

Teorema. Fie punct stationar al lui . Sa presupunem ca functia are derivate partiale de ordinul doi continue intr-o vecinatate a lui .

Daca forma patratica este definita, atunci este un punct de extrem si anume un punct de maxim sau de minim dupa cum sau φ >

Daca forma patratica este nedefinita, atunci nu este punct de extrem al functiei.