| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Transformarile Lorentz .
Consecinte ale transformarilor Lorentz
Introducere . Postulatele lui Einstein
O serie intreaga de experiente efectuate la sfarsitul secolului trecut ( experientele lui Michelson - 1881 , Michelson si Morley - 1887 , Morley si Miller - 1904 ) nu au putut fi interpretate pe baza principiilor generale ale mecanicii newtoniene , evidentiind astfel caracterul limitat al acestora . A aparut necesitatea elaborarii unei noi teorii capabila sa explice consecvent noile fapte experimentale acumulate .
Acest lucru a fost realizat in 1905 de catre Albert Einstein care a formulat doua noi principii generale ( postulate ) care stau la baza teoriei relativitatii restranse .
1.Principiul relativitatii : "Legile fizicii sunt aceleasi in toate sistemele de referinta inertiale" .
2.Principiul constantei luminii in vid : "Viteza luminii in vid are aceeasi valoare in toate directiile si in toate sistemele de referinta inertiale , fiind independenta de miscarea sursei de lumina sau a observatorului" .
Principiile teoriei se refera doar la cazul mai particular al sistemelor de referinta inertiale ( SRI ) , din care cauza se numeste teoria relativitatii restranse . Mai mentionam ca Einstein a construit o teorie care se aplica si sistemelor neinertiale numita teoria relativitatii restranse .
Observatie 1: Primul principiu constituie de fapt o generalizare a principiului relativitatii galileiene din mecanica ( care se refera doar la legile mecanicii ) pentru toate fenomenele fizice . El arata ca in conditii identice un fenomen fizic se desfasoara la fel in SRI diferite. Aceasta inseamna ca prin nici o experienta de fizica nu poate fi pusa in evidenta miscarea rectilinie si uniforma a unui SRI .
Observatie 2: Cel de-al doilea principiu intra in contradictie cu primul . Intr-adevar , daca sursa luminoasa se apropie sau se departeaza de observator cu viteza v , conform legii de compunere a vitezelor data de cinematica newtoniana viteza luminii fata de observator ar trebui sa fie c + v in primul caz si respectiv c - v in al doilea caz . Principiul al doilea al teoriei relativitatii restranse afirma insa ca viteza luminii fata de observator este aceeasi in ambele situatii :
c
= 3 ∙10![]() m/s
m/s
Transformarile Lorentz
Se stie ca transformarile lui Galilei care dau relatiile dintre pozitia si timpul masurate in SRI ( S' ) in miscare si respectiv in SRI ( S ) considerat fix , exprima matematic principiul relativitatii mecanice , deoarece lasa neschimbate ecuatiile dinamicii. Ar parea plauzibil sa consideram ca transformarile lui Galilei ne dau , si in teoria lui Einstein , relatiile de trecere de la un SRI la altul , adica exprima matematic si primul principiu al teoriei relativitatii restranse . Problema esentiala este de a vedea daca aceste transformari nu contrazic principiul constantei luminii in vid . Pentru a putea sa raspundem la aceasta intrebare sa analizam cu atentie consecintele acestui principiu .
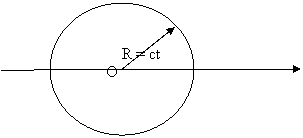
Conform principiului lui Huygens , radiatia luminoasa emisa de o sursa punctiforma se propaga sub forma unei unde sferice , intelegand prin aceasta ca frontul de unda este o suprafata sferica de raza R = ct , unde c este viteza luminii in vid , iar t - timpul necesar luminii sa se propage de la sursa pana la punctul din spatiu atins de frontul de unda . Considerand sursa in originea sistemului de coordonate legate de SRI fix ( S ) , ecuatia acestei suprafete este :
x![]() + y
+ y![]() + z
+ z![]() = R
= R![]() = c
= c![]() t
t![]() . (
2.1 )
. (
2.1 )
In figura 2.1 am reprezentat intersectia sferei cu planul xOy al sistemului de coordonate ales .
![]() y
y
x
Fig. 2.1
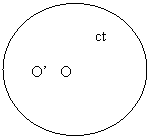
Fie acum SRI mobil ( S' ) care se deplaseaza fata de S cu viteza v dirijata in lungul axei x ( fig. 2.2 ) . Presupunem ca la momentul t = t' = 0 originile O si O' ale celor doua sisteme de coordonate coincid . Pentru un observator care se afla in repaus fata de sistemul ( S ) frontul undei emise la t = 0 din O va fi dupa t secunde suprafata sferica cu centrul in O ( fig. 2.2.a ) de raza ct ( ecuatia 2.1 ) . Pentru observatorul care se gaseste in repaus fata de sistemul ( S' ) conform principiului relativitatii frontul de unda va fi tot o sfera cu centrul in punctul unde a fost emisa lumina in acest sistem , adica punctul O' (fig. 2.2.b) deoarece acesta coincidea cu O la momentul emisiei ( t = t' = 0 ) . Conform principiului al doilea al teoriei relativitatii restranse dupa t' secunde raza R' a frontului de unda va fi ct' deoarece viteza luminii in vid nu depinde de miscarea sistemului de referinta . Prin urmare frontul de unda in acest sistem este reprezentat de ecuatia :
![]() . ( 2.2 )
. ( 2.2 )
Daca transformarile Galilei descriu corect din punct de vedere matematic principiile teoriei relativitatii restranse ele trebuie sa transforme ecuatia ( 2.2 ) in ( 2.1 ) si invers . Aceasta inseamna ca prin inlocuirea lui x' , y' , z' si t' conform relatiilor lui Galilei ecuatia ( 2.2 ) trebuie sa treaca in ( 2.1 ) pentru orice punct din spatiu orice moment de timp . Sa inlocuim aceasta inlocuire :
![]()
sau
![]() . (
2.3 )
. (
2.3 )
Dupa cum se vede imediat , ultima relatie nu poate sa coincida cu ( 2.1 ) pentru orice valoare a lui x ,y ,z si t . In concluzie , transformarea lui Galilei nu ne furnizeaza din punct de vedere al teoriei relativitatii restranse relatiile corecte de trecere de la un SRI la altul .
![]()
![]()
![]()
![]() y y' y y'
y y' y y'
 (S) (S')
(S) (S') 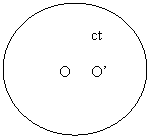 (S) (S')
(S) (S')
 P'(x',y',z')
P'(x',y',z')
 P(x,y,z)
P(x,y,z)
![]()
![]()
x,x' x'
a) b)
Fig. 2.2
Sa
incercam sa modificam relatiile de transformare ( ale lui Galilei ) asa incat
ecuatia ( 2.2 ) sa fie transformata in ( 2.1 ) . Vom admite in
continuare ca y' = y , z' = z deoarece
in relatia ( 2.3 ) termenii cu y![]() si z
si z![]() coincid cu cei din ( 2.2 ) . Comparand ecuatia ( 2.3
) cu ( 2.1 ) apar doua neconcordante : in primul rand coeficientul
lui t
coincid cu cei din ( 2.2 ) . Comparand ecuatia ( 2.3
) cu ( 2.1 ) apar doua neconcordante : in primul rand coeficientul
lui t![]() nu mai este c
nu mai este c![]() , iar in membrul stang apare termenul suplimentar ( - 2xvt ) . Acest termen suplimentar se
datoreaza faptului ca x' se
exprima si prin x si
prin t . Aceasta dificultate
poate fi eliminata doar daca admitem ca si t' se exprima prin x si t , astfel
incat
, iar in membrul stang apare termenul suplimentar ( - 2xvt ) . Acest termen suplimentar se
datoreaza faptului ca x' se
exprima si prin x si
prin t . Aceasta dificultate
poate fi eliminata doar daca admitem ca si t' se exprima prin x si t , astfel
incat ![]() sa introduca la randul sau un termen
proportional cu produsul xt care
sa compenseze termenul suplimentar din ( 2.3 ) . Vom cauta t de forma :
sa introduca la randul sau un termen
proportional cu produsul xt care
sa compenseze termenul suplimentar din ( 2.3 ) . Vom cauta t de forma :
t' = ft - gx ,
unde constanta f trebuie sa fie pozitiva deoarece in orice sistem de
referinta evolutia in timp trebuie sa se
desfasoare de la trecut spre viitor . Observand ca ![]() contine si
termeni in
contine si
termeni in ![]() va trebui sa
modificam putin si expresia lui x' luand :
va trebui sa
modificam putin si expresia lui x' luand :
x' = h(x - vt )
( f , g , h constante care trebuie determinate) . Introducand in ( 2.2 ) se obtine :
![]()
care coincide cu ( 2.1 ) pentru orice punct din spatiu si orice moment daca f , g , h satisfac ecuatiile :
![]() (a)
(a)
![]() (b) ( 2.4 )
(b) ( 2.4 )
![]() (c)
(c)
Inmultind ( 2.4.a ) cu v si inlocuind pe vh![]() in ( 2.4.b ) obtinem
in ( 2.4.b ) obtinem ![]() .
.
Inmultind apoi ( 2.4.b ) cu v si inlocuind vh![]() in ( 2.4.c ) rezulta
in ( 2.4.c ) rezulta ![]()
Raportul ultimelor doua ecuatii ne da ![]() sau
sau ![]() .
.
Inlocuind pe g in ( 2.4.b ) rezulta h = f . Din relatia ( 2.4.c ) obtinem atunci :
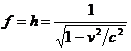 , adica
, adica 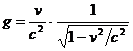 .
.
Cu aceste valori pentru constantele f , g si h obtinem relatiile :
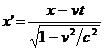 , y' = y , z' = z ,
, y' = y , z' = z , 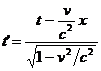 , ( 2.5 )
, ( 2.5 )
cunoscute sub numele de transformarile lui Lorentz . Este evident ca a afirma ca un SRI (S') se misca fata de SRI (S) cu viteza v , este echivalent cu a spune ca SRI (S) se misca fata de SRI (S') cu viteza (- v) . Deoarece relatiile ( 2.5 ) sunt valabile pentru viteza constanta v oarecare , relatiile de trecere de la SRI (S') la SRI (S) se obtin din ( 2.5 ) inlocuind pe v cu (- v) , adica :
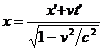 , y = y' ,
z'
= z ,
, y = y' ,
z'
= z , 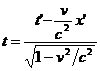 . ( 2.5 )'
. ( 2.5 )'
Expresiile ( 2.5 )' trec aproximativ in transformarile
lui Galilei daca viteza v dintre
cele doua sisteme de referinta este aproximativ mica in raport
cu viteza luminii in vid (![]() putem considera
putem considera ![]() ) . Aceasta justifica faptul ca transformarile
lui Galilei conduc la rezultate practic corecte pentru viteze uzuale ,
intelegand prin aceasta chiar si rachetele care se misca cu
a doua viteza cosmica ( 11,2 km/s ) sau Pamantul in
miscarea pe ecliptica ( 30 km/s ) .
) . Aceasta justifica faptul ca transformarile
lui Galilei conduc la rezultate practic corecte pentru viteze uzuale ,
intelegand prin aceasta chiar si rachetele care se misca cu
a doua viteza cosmica ( 11,2 km/s ) sau Pamantul in
miscarea pe ecliptica ( 30 km/s ) .
Consecintele fizice ale transformarilor Lorentz
Contractia lungimilor
Dupa cum se stie masurarea unei distante revine la a determina de cate ori o lungime aleasa ca etalon este cuprinsa in acea distanta .
Sa consideram o rigla , care se afla in
repaus fata de SRI (S') , asezata in lungul axei Ox si care are lungimea l0 in acest sistem . Notand cu ![]() si
si ![]() punctele in care se
gasesc cele doua capete ale riglei avem ca l0 =
punctele in care se
gasesc cele doua capete ale riglei avem ca l0 = ![]() -
-![]() . Sa vedem acum care este lungimea riglei pe acre o
masoara un observator situat in S . Pentru aceasta trebuie
determinata pozitia capetelor riglei in S la acelasi moment de
timp in sistem . Pentru aceasta trebuie sa cunoastem simultan ( la
momentul t1 = t2 )
coordonatele capetelor riglei x1
si x2 . Conform
relatiilor ( 2.5 ) avem :
. Sa vedem acum care este lungimea riglei pe acre o
masoara un observator situat in S . Pentru aceasta trebuie
determinata pozitia capetelor riglei in S la acelasi moment de
timp in sistem . Pentru aceasta trebuie sa cunoastem simultan ( la
momentul t1 = t2 )
coordonatele capetelor riglei x1
si x2 . Conform
relatiilor ( 2.5 ) avem :
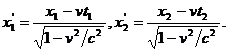
Scazand aceste relatii si avand in vedere ca t1 = t2 obtinem
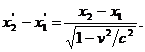
Tinand cont ca ( x2 - x1 ) reprezinta lungimea l a riglei in sistemul S , rezulta
![]() (
2.6 )
(
2.6 )
Deoarece ![]() este mai mic decat unu
,rezulta ca pentru observatorul fata de care rigla se
misca cu viteza v ,
lungimea riglei este micsorata ( l
< l0 ) . Din acest motiv relatia ( 2.6 ) reprezinta
contractia lungimilor . Atragem atentia ca daca am
considera rigla de lungime l0
in repaus in S atunci pentru un observator din S' ea apare de asemenea
contractata cu factorul
este mai mic decat unu
,rezulta ca pentru observatorul fata de care rigla se
misca cu viteza v ,
lungimea riglei este micsorata ( l
< l0 ) . Din acest motiv relatia ( 2.6 ) reprezinta
contractia lungimilor . Atragem atentia ca daca am
considera rigla de lungime l0
in repaus in S atunci pentru un observator din S' ea apare de asemenea
contractata cu factorul ![]() . Acest rezultat se
obtine printr-un rationament analog plecand de la relatiile (
2.5 )' deoarece se poate considera de asemenea ca S' se misca cu
viteza ( -v ) fata de S .
. Acest rezultat se
obtine printr-un rationament analog plecand de la relatiile (
2.5 )' deoarece se poate considera de asemenea ca S' se misca cu
viteza ( -v ) fata de S .
Mentionam ca aceasta contractie apare numai dupa directia de miscare deoarece in demonstratie am folosit ipoteza ca rigla este asezata in lungul acestei directii . In cazul in care rigla este asezata perpendicular pe directia de miscare , atunci l = l0 , deoarece , conform relatiei ( 2.5 ) , y' = y si z' = z .
Observam ca rigla are lungimea mai mare in sistemul fata de care se afla in repaus, denumit sistem propriu . Acestei lungimi i se mai spune si lungime proprie sau de repaus . Deoarece contractia Lorentz are loc numai dupa directia de miscare , un corp care are volumul V0 in sistemul propriu va avea un volum
V = V0![]()
in sistemul fata de care corpul se misca cu viteza v .
Faptul ca distanta dintre doua puncte apare diferita dupa cum este considerata intr-un SRI sau altul ( in miscare fata de celalalt ) , face necesara revizuirea conceptiilor newtoniene asupra spatiului . Intr-adevar , spatiul relativ ca parte componenta a spatiului aparent nu mai poate fi in nici un fel confundat cu acesta limitandu-se astfel realitatea fizica a spatiului absolut . Apare clar legatura stransa intre proprietatile spatiului si miscarea corpurilor materiale . In afara de aceasta , deoarece , conform principiului relativitatii , prin nici o experienta fizica nu se poate pune in evidenta miscarea unui SRI fata de altul ( deci nici fata de spatiul absolut ! ) rezulta ca putem folosi miscarea sistemelor inertiale pentru marcarea succesiva prin mijloace fizice a punctelor din spatiu .
Dilatarea duratelor
Am vazut ca distantele spatiale au valori diferite in diferite sisteme inertiale . Apare naturala intrebarea daca nu cumva si cu duratele se intampla acelasi lucru . Pentru aceasta sa consideram doua evenimente acre au loc in acelasi punct din sistemul ( S' )la momentele t1' si respectiv t2' fiind despartite de intervalul de timp ∆t0 = t2' - t1' . Notand cu t2 si respectiv t1 momentele corespunzatoare din SRI ( S ) , fata de care ( S' ) se misca cu viteza v , intervalul de timp in acest sistem va fi ∆t0 = t2 - t1 . Conform relatiilor ( 2.5 )
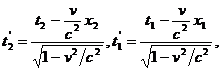
unde x1 si x2 sunt punctele in care se petrec cele doua evenimente pentru un observator din sistemul ( S ) , la momentele t1 si respectiv t2 . Scazand relatiile de mai sus , obtinem :
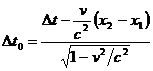 ( 2.7 )
( 2.7 )
Diferenta x2 - x1 o calculam folosind din nou relatiile ( 2.5 ) :
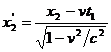 ,
, 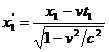 ,
,
unde x1' si x2' sunt punctele din ( S' ) in care au loc cele doua evenimente . Deoarece am considerat ca aceste evenimente se petrec in acelasi punct din ( S' ) , x1' = x2' . Scazand ultimele doua relatii rezulta :
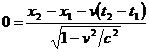 adica x2 - x1 = v∆t .
adica x2 - x1 = v∆t .
Introducand pe x2 - x1 in ecuatia ( 2.7 ) , obtinem :
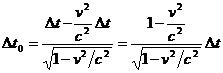
sau
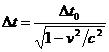 , ( 2.8
)
, ( 2.8
)
Din formula ( 2.8 ) rezulta faptul ca intervalul de timp ∆t dintre cele doua evenimente este mai mare in sistemul ( S ) decat in sistemul ( S' ) ( care se misca cu viteza v fata de S ) in care evenimentele au loc in acelasi punct .
Desigur ca nu ne putem astepta sa putem
pune in evidenta dilatarea duratei prin efectuarea unei
experiente in sistemele de referinta in miscare rectilinie
si uniforma fata de Pamant ( automobil , tren ,
racheta etc. ) care ne stau la dispozitie in mod obisnuit . Intr-adevar
, in aceste cazuri raportul v/c este
mult mai mic si deci radicalul ![]() poate fi foarte bine
aproximat prin unu .
poate fi foarte bine
aproximat prin unu .
O confirmare experimentala a aparut insa in urma observatiilor efectuate asupra timpului de viata a mezonilor μ din radiatia cosmica , care se misca fata de Pamant cu viteze aproximativ 0,9998 c . Mezonii μ sunt particule instabile care apar in urma ciocnirilor si dezintegrarilor altor particule . Intervalul de timp dintre aparitia si disparitia ( dezintegrarea ) lor se numeste timp de viata si poate fi determinat experimental .
Se pot produce mezoni μ si in conditii de
laborator . Timpul lor de viata masurat in sistemul legat de
Pamant este de aproximativ 2∙10![]() s .
s .
Legea relativista de compunere a vitezelor
Sa consideram un punct material care are coordonatele ( x , y , z ) in SRI ( S ) si respectiv ( x' , y' , z' ) in SRI ( S' ) care se misca fata de ( S ) rectiliniu si uniform , in lungul axei Ox , cu viteza v . Daca presupunem ca punctul material se misca paralele cu axa Ox , el va avea viteza u = dx/dt in sistemul ( S ) , respectiv u' = dx'/dt' in ( S' ) . Scriind transformarea Lorentz pentru coordonata x ( 2.5 ) la momentele de timp t si respectiv t + dt avem :
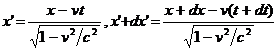 .
.
Scazand prima relatie din cea de-a doua obtinem :
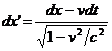 . (
2.9 )
. (
2.9 )
Analog se obtine o relatie pentru timp :
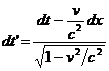 . (
2.10 )
. (
2.10 )
Impartind membru cu membru relatia ( 2.9 ) la ( 2.10 ) rezulta :
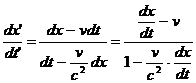 .
.
Avand in vedere relatiile de definitie ale lui u si u' , din ultima relatie obtinem legea relativista de compunere a vitezelor paralele :
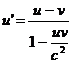 . (
2.11 )
. (
2.11 )
Se vede imediat ca aceasta relatie satisface principiul constantei vitezei luminii in vid . Intr-adevar , punand in ( 2.11 ) u = c se obtine u' = c .
4. Concluzii
Asadar , teoria relativitatii impune noi conceptii asupra spatiului si timpului , care mai departe au condus la o modificare a cinematicii , a dinamicii newtoniene etc.
Manolea Valentin
Ghilea Ionut
Dragoi Bogdan
Mosneanu Ion - Cosmin
Clasa a XII-a A
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 15187
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved