| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Variabile aleatoare
Pana acum, in studiul campului de evenimente atasat unui experiment, ne-am ocupat in special, de aparitia sau neaparitia evenimentelor, asadar de latura calitativa a experimentului.
Pentru studiul matematic al fenomenelor aleatoare, este necesar ca descrierea acestora sa aiba expresii cantitative, care sa poata fi tratate din punct de vedere matematic. Aceasta expresie cantitativa a fenomenului aleator este data de variabila aleatoare.
Definitia 3.1.
Fie campul de probabilitate ![]() . Numim variabla aleatoare de tip discret o
aplicatie
. Numim variabla aleatoare de tip discret o
aplicatie ![]() , care satisface urmatoarele conditii:
, care satisface urmatoarele conditii:
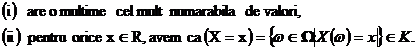
Observatia 3.2 Daca avem ca ![]() , atunci conditia (ii) este automat indeplinita.
, atunci conditia (ii) este automat indeplinita.
Observatia 3.3 Se poate arata ca:
![]()
este variabila aleatoare de tip discret si poarta numele de indicatoarea evenimentului A.
Observatia 3.4 Daca o variabila aleatoare de tip discret ia un numar finit de valori, vom spune ca este o variabila aleatoare simpla.
Definitia 3.5. Numim distributia sau repartitia variabilei aleatoare X de tip discret, tabloul
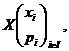
unde xi![]() R,
R, ![]() , sunt valori pe care le ia vriabila aleatoare X, iar pi este probabilitatea cu care variabila aleatoare X ia valoarea xi, adica
, sunt valori pe care le ia vriabila aleatoare X, iar pi este probabilitatea cu care variabila aleatoare X ia valoarea xi, adica ![]() pentru fiecare
pentru fiecare ![]() .
.
Observatia 3.6 Deoarece
evenimentele ![]() ,
, ![]() , formeaza un sistem complet de evenimente, avem ca
, formeaza un sistem complet de evenimente, avem ca
![]() .
.
Observatia 3.7 In teoria probabilitatilor si in aplicatiile acesteia, se intalnesc clase de variabile aleatoare de tip discret. Forma cea mai generala a unei variabile aleatoare apartinand unei clase se numeste lege de probabilitate de tip discret.
Definitia 3.8 Spunem ca variabila aleatoare X de tip discret urmeaza legea binomiala, daca are distributia
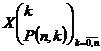 , unde
, unde ![]() , iar
, iar ![]() .
.
Observatia 3.9 Probabilitatile
![]() , ce intervin in distributia lui X, sunt cele de la schema lui Berboulli cu bila intoarsa
(binomiala).
, ce intervin in distributia lui X, sunt cele de la schema lui Berboulli cu bila intoarsa
(binomiala).
Definitia 3.10. Spunem ca variabila alatoare X de tip discret urmeaza legea hipergeometrica, daca are distributia
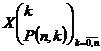 , unde
, unde ![]() , iar
, iar ![]() .
.
Observatia 3.11. Probabilitatile ![]() , din distributia lui X, sunt cele de la schema lui Bernoulli cu bila neintoarsa.
, din distributia lui X, sunt cele de la schema lui Bernoulli cu bila neintoarsa.
Observatia 3.12 Daca
se noteaza ![]() si
si ![]() , iar
, iar ![]() , atunci
, atunci ![]() , adica se obtine distributia binomiala.
, adica se obtine distributia binomiala.
Definitia 3.13. Spunem ca variabila aleatoare X de tip discret urmeaza legea lui Poisson, daca are distributia
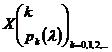 , unde
, unde ![]() iar
iar ![]()
Teorema 3.14.(Poisson). Daca variabila aleatoare X urmeaza legea binomiala, adica are distributia
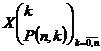 , unde
, unde ![]() ,
,
si daca ![]() , astfel incat
, astfel incat ![]() , atunci pentru
, atunci pentru ![]() urmeaza legea lui Poisson, adica
urmeaza legea lui Poisson, adica ![]()
Demonstratie.
Scriem succesiv, avand in veder ca ![]() si
si ![]() , urmatoarele relatii
, urmatoarele relatii
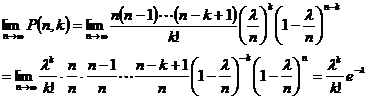 .
.
Daca retinem extremitatile acestui sir de egalitati, se obtine afirmatia din teorema.
Observatia 3.15 Deoarece ![]() , rezulta ca pentru n mare, probabilitatea pn
este mica. Prin urmare, probabilitatea de aparitie a evenimentului,
caruia i se ataseaza, fiind mica, legea lui Poisson se mai
numeste si legea evenimentelor rare.
, rezulta ca pentru n mare, probabilitatea pn
este mica. Prin urmare, probabilitatea de aparitie a evenimentului,
caruia i se ataseaza, fiind mica, legea lui Poisson se mai
numeste si legea evenimentelor rare.
Defintia 3.16 Spunem ca variabla aleatoare X de tip discret urmeaza legea lui Pascal, daca are distributia
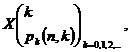 cu
cu ![]()
iar ![]() si q=1-
p.
si q=1-
p.
Observatia 3.17 Probabilitatile ![]() din distributia
lui X sunt cele de la schema lui
Pascal.
din distributia
lui X sunt cele de la schema lui
Pascal.
Observatia 3.18. In cazul particular n = 1, vom spune ca variabila aleatoare X urmeaza legea geometrica.
Definitia 3.19 Fie
campul de probabilitate ![]() . Spunem ca
. Spunem ca ![]() este vector aleator bidimansional de tip discret, daca
aplicatia
este vector aleator bidimansional de tip discret, daca
aplicatia ![]() R2,
satisface conditiile
R2,
satisface conditiile
(i) are o multime cel mult numarabila de valori,
(ii)
pentru
orice ![]() R2,
avem ca
R2,
avem ca
![]()
Definitia 3.20 Numim
distributia sau repartitia vectorului aleator ![]() de tip discret, tabloul bidimensional
de tip discret, tabloul bidimensional
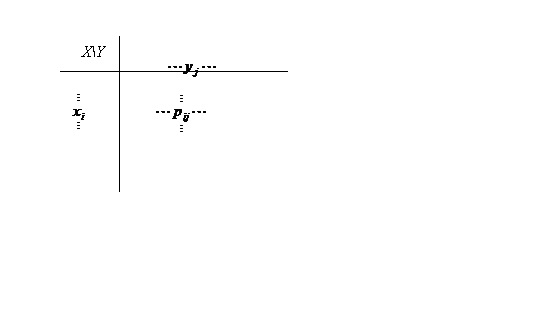
unde ![]() sunt valorile pe care le ia vectorul aleator
sunt valorile pe care le ia vectorul aleator ![]() , iar pij
sunt probabilitatile cu care sunt luate aceste valori, adica
putem scrie
, iar pij
sunt probabilitatile cu care sunt luate aceste valori, adica
putem scrie ![]() .
.
Definitia 3.21 Spunem ca variabilele aleatoare X si Y care au respectiv distributiile
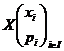 si
si 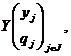
sunt independente, daca ![]() pentru orice
pentru orice ![]() adica
adica ![]()
Definitia 3.22 Fie variabilele aleatoare X si Y care au respectiv distributiile
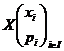 si
si 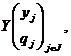
atunci variabilele aleatoare
suma, X+Y, produs XY, si respectiv cat, ![]() (daca
(daca ![]() ), vor avea distributiile
), vor avea distributiile
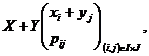
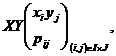
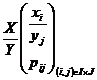 ,
,
unde ![]()
Observatia 3.23. Daca
variabilele aleatoare X si Y sunt independente, atunci ![]() pentru orice
pentru orice ![]() .
.
Observatia 3.24. Urmatoarele relatii au loc
![]() respectiv
respectiv ![]()
Exemplul 3.25 Doua
masini produc piese de acelasi tip, iar probabilitatea ca o
piesa produsa de fiecare din cele doua masini sa fie
defecta este ![]() , iar probabilitatea ca sa nu fie defecta este
, iar probabilitatea ca sa nu fie defecta este ![]() . Daca prima masina a produs m piese, iar a doua masina a
produs n piese, fie X numarul pieselor defecte produse
de prima masina si respectiv Y
numarul pieselor defecte produse de a doua masina. Variabilele
aleatoare X si Y sunt independente si urmeaza
fiecare legea binomiala, respectiv cu distributiile
. Daca prima masina a produs m piese, iar a doua masina a
produs n piese, fie X numarul pieselor defecte produse
de prima masina si respectiv Y
numarul pieselor defecte produse de a doua masina. Variabilele
aleatoare X si Y sunt independente si urmeaza
fiecare legea binomiala, respectiv cu distributiile
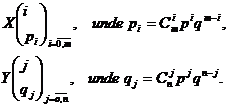
Numarul total al pieselor defecte produse de cele doua masini va fi dat prin variabila aleatoare suma, X+Y, care are distributia
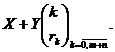
Avand in vedere ca variabilele aleatoare X si Y sunt independente, probabilitatile ![]() din distributia variabilei aleatoare X+Y se calculeaza dupa cum
urmeaza
din distributia variabilei aleatoare X+Y se calculeaza dupa cum
urmeaza
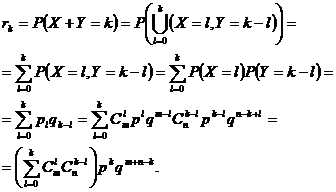
Se stie ca ![]() prin urmare
prin urmare ![]() pentru fiecare
pentru fiecare ![]() S-a obtinut
astfel ca numarul pieselor defecte produse de cele doua
masini impreuna este o variabila aleatoare ce urmeaza tot
legea binomiala.
S-a obtinut
astfel ca numarul pieselor defecte produse de cele doua
masini impreuna este o variabila aleatoare ce urmeaza tot
legea binomiala.
Definitia 3.26 Fie campul de probabilitate ![]() Numim variabila
aleatoare, aplicatia
Numim variabila
aleatoare, aplicatia ![]() R, daca satisface conditia ca pentru orice
R, daca satisface conditia ca pentru orice ![]() R avem
R avem ![]()
Definitia 3.27. Fie campul de probabilitate ![]() Spunem ca
Spunem ca ![]() este vector aleator bidimensional, daca este o aplicatie
este vector aleator bidimensional, daca este o aplicatie
![]() R2,
care satisface conditia ca orice
R2,
care satisface conditia ca orice ![]() R2 sa avem
R2 sa avem ![]()
Observatia 3.28 Daca X si Y sunt
variabile aleatoare, atunci si ![]() sunt variabile
aleatoare.
sunt variabile
aleatoare.
Definitia 3.29. Numim functie de repartitie atasata variabilei aleatoare X, functia
![]() definita prin
definita prin ![]() pentru orice
pentru orice ![]()
Observatia 3.30. Daca
variabila aleatoare X este de tp
discret, deci are distributia 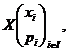 atunci functia de repartitie este data prin
formula
atunci functia de repartitie este data prin
formula
![]()
Aici notatia
prescurtata a sumei indica faptul ca pentru un ![]() dat, se aduna
toate probabilitatile
dat, se aduna
toate probabilitatile ![]() ce corespund valorilor
lui X, care verifica
conditia
ce corespund valorilor
lui X, care verifica
conditia ![]()
Proprietatea 3.31 Fie X o variabila aleatoare si F functia de repartitie corespunzatoare, atunci urmatoarele afirmatii sunt adevarate:
(1) pentru orice ![]() , avem ca
, avem ca ![]()
(2) pentru orice a, b![]() R, a<b, avem ca
R, a<b, avem ca
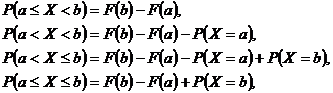
(3) pentru orice ![]()
(functia F este descrescatoare),
(4) ![]()
(5) pentru orice ![]() , avem ca
, avem ca ![]()
(functia F este continua la stanga).
Demonstratie. (1) Deoarece valorile functiei de
repartitie sunt niste probabilitati, avem aceasta
afirmatie, deci ![]()
(2) Se scrie succesiv
![]()
Deoarece ![]() avem in continuare
ca
avem in continuare
ca
![]()
Pentru a doua relatie se are in vedre ca
![]()
deci
![]()
In mod analog, se arata si celelalte doua relatii de la acest punct.
(3) Folosind prima formula de la punctul precedent, avem relatiile
![]() de unde
de unde ![]()
(4) Formal avem ca ![]() respectiv
respectiv
![]()
(5) Un ratioanament analog cu cel de la punctul precedent ne conduce la faptul ca functia F este continua la stanga.
Observatia 3.32 Functia de repartitie F
a unei variabile aleatoare X de tip
discret, care are distributia 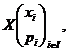 este, conform Observatiei
3.30., o functie in scara, avand punctele
este, conform Observatiei
3.30., o functie in scara, avand punctele ![]() puncte de
discontinuitate, iar marimile salturilor in aceste puncte de
discontinuitate sunt respectiv probabilitatile
puncte de
discontinuitate, iar marimile salturilor in aceste puncte de
discontinuitate sunt respectiv probabilitatile ![]()
Exemplul 3.33 Variabila
aleatoare X cu distributia
urmatoare 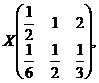 are functia de repartitie
are functia de repartitie
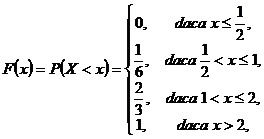
care are graficul in fig. 3.1.
Definitia 3.34. Numim
functie de repartitie atasata vectorului aleator
bidimensional ![]() functia
functia
![]()
0 1 2 3 x

fig.3.1.
Observatia 3.35 Proprietatile de la functia de repartitie pentru o variabila aleatoare le regasim si la functia de repartitie a unui vector aleator bidimansional, anume
(1) pentru orice ![]() R2,
avem ca
R2,
avem ca 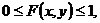
(2) pentru orice a < b, avem ca
![]()
(3) functia ![]() este nedescrescatoare in raport cu fiecare argumant,
este nedescrescatoare in raport cu fiecare argumant,
(4) ![]()
![]()
(5) functia ![]() este continua la stanga in raport cu fiecare argumant.
este continua la stanga in raport cu fiecare argumant.
Observatia 3.36. Daca vactorul aleator bidimensional ![]() are functia de
repartitie F, iar variabilele
aleatoare componente X si Y au respectiv functiile de
repartitie
are functia de
repartitie F, iar variabilele
aleatoare componente X si Y au respectiv functiile de
repartitie ![]() si
si ![]() , atunci avem ca
, atunci avem ca
![]()
Definitia 3.37. Fie variabila aleatoare X avand functia de repartitie F. Vom spune ca X este variabila aleatoare de tip continuu, daca functia de repartitie F se poate reprezenta sub forma
![]()
functia ![]() numindu-se densitate
de probabilitate a variabilei aleatoare X.
numindu-se densitate
de probabilitate a variabilei aleatoare X.
Propozitia 3.38 Fie
variabila aleatoare X de tip
continuu, avand functia de repartitie F si densitatea de probabilitate ![]() , atunci sunt adevarate urmatoarele afirmatii:
, atunci sunt adevarate urmatoarele afirmatii:
(1) pentru orice ![]() avem ca
avem ca ![]()
(2) ![]()
(3) pentru a < b, avem ca 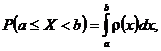
(4) ![]()
Cele patru proprietati rezulta imediat din Propozitia 3.31.
Observatia 3.39. Daca
variabila aleatoare X este de tip
continuu, atunci ![]() pentru orice
pentru orice ![]() . Prin urmare, in acest caz avem ca
. Prin urmare, in acest caz avem ca
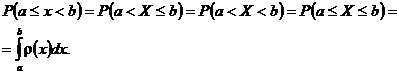
Observatia 3.40. Daca
variabila aleatoare X de tip continuu
are functia de repartitie F
si densitatea de probabilitate![]() , atunci se poate scrie succesiv
, atunci se poate scrie succesiv
![]()
Asadar, cand ![]() este mic, avem ca
este mic, avem ca ![]()
Definitia 3.41 Fie vectorul aleator ![]() avand functia de repartitie
F. Spunem ca U este vector aleator de tip continuu,
daca functia de repartitie F
se poate reprezenta sub forma
avand functia de repartitie
F. Spunem ca U este vector aleator de tip continuu,
daca functia de repartitie F
se poate reprezenta sub forma
![]()
functia ![]() numindu-se densitate
de probabilitate a vectorului
numindu-se densitate
de probabilitate a vectorului
Observatia 3.42. Daca
vectorul aleator ![]() este de tip continuu,
avand functia de repartitie F
si densitatea de probabilitate
este de tip continuu,
avand functia de repartitie F
si densitatea de probabilitate![]() , iar variabilele aleatoare componente X si Y au respectiv
densitatile de probabiliate
, iar variabilele aleatoare componente X si Y au respectiv
densitatile de probabiliate ![]() si
si ![]() , atunci
, atunci
(1) pentru orice ![]() avem ca
avem ca ![]()
(2) ![]()
(3) pentru orice ![]() avem
avem ![]()
(4) ![]()
(5) ![]() si
si ![]()
Observatia 3.43 Ca si la variabilele aleatoare de tip discret si la cele de tip continuu exista clase de variabile aleatoare. Forma cea mai generala a densitatii de probabilitate a unei variabile aleatoare din clasa respectiva, ne da o lege de probabilitate de tip continuu.
Definitia 3.44. spunem ca variabila aleatoare X urmeaza legea uniforma pe intervalul [a,b], daca are densitatea de probabilitate
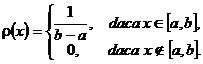
Observatia 3.45. Functia de repartitie pentru variabila aleatoare X, ce urmeaza legea uniforma pe intervalul [a,b] este
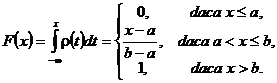
Definitia 3.46 Spunem ca vectorul aleator ![]() urmeaza legea uniforma pe domeniul
urmeaza legea uniforma pe domeniul ![]() daca
are densitatea de probabilitate
daca
are densitatea de probabilitate
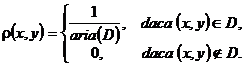
Observatia
3.47. Daca ![]() atunci
atunci
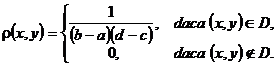
De asemena, in acest caz, folosind Observatia 3.42, punctul (5), avem ca
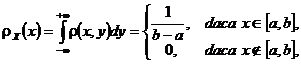
adica variabila
aleatoare X urmeaza legea
uniforma pe intervalul ![]() . In mod
anolog, se arata ca variabila aleatoare Y urmeaza legea uniforma pe intervalul
. In mod
anolog, se arata ca variabila aleatoare Y urmeaza legea uniforma pe intervalul ![]()
Definitia 3.48. Spunem ca variabila aleatoare X
urmeaza legea normala (legea lui Gauss) de parametrii ![]() si
si ![]() notam aceasta prin
notam aceasta prin ![]() daca are densitatea de probabilitate
daca are densitatea de probabilitate
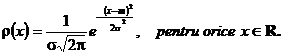
Observatia 3.49 Reprezentarea grafica a densitatii de probabilitate ![]() , este data in fig. 3.2. Curba ce reprezinta
graficul lui
, este data in fig. 3.2. Curba ce reprezinta
graficul lui ![]() poarta denumirea
de curba lui Gauss si care modeleaza foarte multe din fenomenele
aleatoare.
poarta denumirea
de curba lui Gauss si care modeleaza foarte multe din fenomenele
aleatoare.

fig.3.2.
Observatia 3.50. Daca variabila aleatoare X urmeaza legea normala ![]() atunci
functia de repartitie F este data prin
atunci
functia de repartitie F este data prin
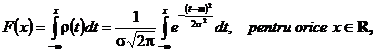
si are graficul dat in fig.3.3.
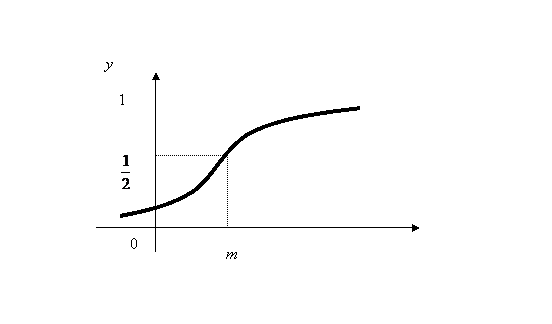
fig.3.3.
Observatia 3.51 Daca variabila aleatoare X
urmeaza legea normala ![]() atunci spunem ca urmeaza legea
normala redusa.
atunci spunem ca urmeaza legea
normala redusa.
Observatia 3.52 Pentru calculul valorilor functiei de repartitie se
foloseste formula ![]() unde functia
unde functia ![]() se numeste functia lui Laplace
si este definita prin
se numeste functia lui Laplace
si este definita prin
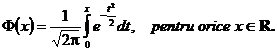
Intr-adevar,
daca se face schimbarea de variabila ![]() se poate scrie succesiv
se poate scrie succesiv
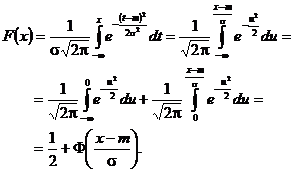
Observatia 3.53. Functia lui Laplace ![]() este tabelata in Anexa I, pentru
argumente pozitive. Daca x <
0, atunci
este tabelata in Anexa I, pentru
argumente pozitive. Daca x <
0, atunci ![]()
Definitia 3.54. Spunem ca variabila
aleatoare X urmeaza legea
exponentiala de parametru ![]() daca are densitatea de probabilitate
daca are densitatea de probabilitate
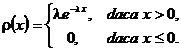
Definitia 3.55. Variabila aleatoare X urmeaza legea gamma, daca are densitatea de probabilitate
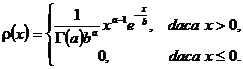
cu parametrii a, b >0, iar ![]() este functia lui Euler de speta a
doua, adica
este functia lui Euler de speta a
doua, adica
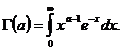
Observatia 3.56. In cazul particular ![]() se obtine legea exponentiala.
se obtine legea exponentiala.
Definitia 3.57. Variabila aleatoare X urmeaza legea ![]() (hi -
patrat), daca are densitataea de probabilitate
(hi -
patrat), daca are densitataea de probabilitate
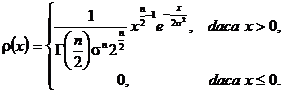
unde parametrul ![]() iar
iar ![]() , si
poarta numele de numarul gradelor de libertate.
, si
poarta numele de numarul gradelor de libertate.
Observatia 3.58. Legea ![]() denumita si legea Herbert - Pearson,
este un caz particular al legii gamma, anume, pentru
denumita si legea Herbert - Pearson,
este un caz particular al legii gamma, anume, pentru ![]() si
si ![]()
Definitia 3.59. Variabila aleatoare X urmeaza legea Student (Gosset) cu n grade de libertate, daca are densitatea de probabilitate
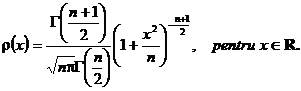
Observatia 3.60. In cazul particular ![]() se obtine legea
lui Cauchy, care are densitatea de probabilitate
se obtine legea
lui Cauchy, care are densitatea de probabilitate
![]()
Definitia 3.61. Variabila aleatoare X urmeaza legea beta, daca are densitatea de probabilitate
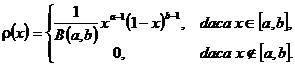
cu parametrii ![]() unde
unde ![]() este functia lui Euler de speta
intai, adica
este functia lui Euler de speta
intai, adica
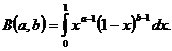
Definitia 3.62. Spunem ca variabilele aleatoare X si Y sunt independente, daca
![]()
unde functia F este functia de repartitie a
vectorului aleator![]() , iar
, iar ![]() si respectiv
si respectiv ![]() sunt functile de
repartitie ale variabileleo aleatoare componente X si Y.
sunt functile de
repartitie ale variabileleo aleatoare componente X si Y.
Observatia 3.63 Definitia 3.62. pentru cazul discret este echivalenta cu Definitia 3.21.
Proprietatea 3.64 Fie variabilele aleatoare X si Y de tip continuu, atunci X si Y sunt independente daca si numai daca are loc
![]()
unde ![]() este densitatea de
probabilitate a vectorului aleator
este densitatea de
probabilitate a vectorului aleator ![]() , iar
, iar ![]() si
si ![]() sunt respectiv
densitatile de probabilitate ale variabilelor aleatoare X si Y.
sunt respectiv
densitatile de probabilitate ale variabilelor aleatoare X si Y.
Demonstratie. Daca variabilele aleatoare X si Y sunt independente, conform Definitiei 3.62., avem ca ![]() Daca derivam
aceasta relatie in raport cu x
si respectiv y, rezulta
ca
Daca derivam
aceasta relatie in raport cu x
si respectiv y, rezulta
ca
![]()
deci ![]()
Afirmatia inversa rezulta din scrierea succesiva
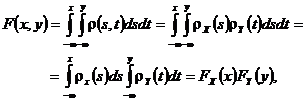
deci ![]()
Propozitia 3.65. Daca vectorul aleator ![]() are densitatea de
probabilitate
are densitatea de
probabilitate ![]() , atunci densitatea de probabilitate
, atunci densitatea de probabilitate ![]() a variabilei aleatoare
a variabilei aleatoare
![]() este data prin
este data prin
![]()
Demonstratie. Scriem functia de repartitie ![]() a variabilei aleatoare Z,
anume
a variabilei aleatoare Z,
anume
![]()
Domeniul de integrare pe care se ia inegral dubla este cel hasurat in fig.3.5.
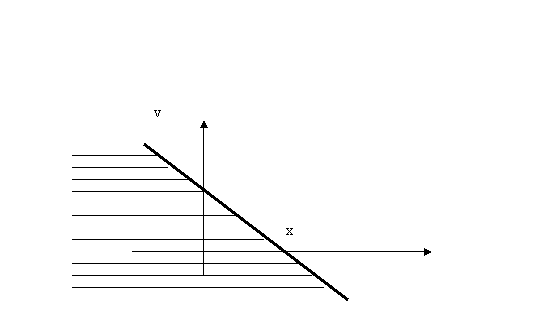
fig.3.5.
Astfel avem 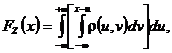 care prin derivare
conduce la
care prin derivare
conduce la
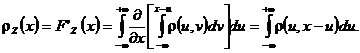
Prin urmare avem ca ![]()
Observatia 3.66. Daca variabilele aleatoare X si Y sunt independentes, atunci ![]() prin urmare
prin urmare
![]()
Observatia 3.67. Analog se arata ca daca ![]() si
si ![]() iar
iar ![]() este densitatea de
probabilitate a vectorului aleator
este densitatea de
probabilitate a vectorului aleator ![]() , atunci
, atunci
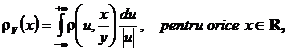
respectiv
![]()
Proprietatea 3.68 Fie variabila aleatoare X cu densitatea de probabilitate ![]() si functia
si functia ![]() strict monotona,
atunci variabila aleatoare
strict monotona,
atunci variabila aleatoare ![]() are densitatea de
probabilitate data prin
are densitatea de
probabilitate data prin
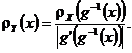
Demonstratie. Daca functia g este strict crescatoare, avem ca
![]()
adica ![]() Prin derivare
rezulta
Prin derivare
rezulta
![]()
Deoarece functia ![]() este crescatoare,
avem
este crescatoare,
avem ![]() deci
deci
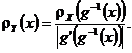
Analog se procedeaza
si cand functia ![]() este strict
descrescatoare.
este strict
descrescatoare.
Aplicatia 3.69 Daca ![]() avem ca
avem ca ![]() este stict
monotona si are inversa
este stict
monotona si are inversa 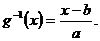 De asemenea, avem
ca
De asemenea, avem
ca ![]() Folosind formula de la
proprietatea precedenta se obtine ca
Folosind formula de la
proprietatea precedenta se obtine ca
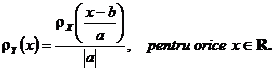
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2222
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved