| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Exercitii si probleme propuse
1. Se aruncǎ o monedǎ
de patru ori. Fie ![]() evenimentul ca marca
sǎ aparǎ de douǎ ori,
evenimentul ca marca
sǎ aparǎ de douǎ ori, ![]() evenimentul ca marca
sǎ aparǎ cel puti o datǎ,
evenimentul ca marca
sǎ aparǎ cel puti o datǎ, ![]() evenimentul ca marca
sǎ aparǎ la aruncarea a doua. Sǎ se determine:
evenimentul ca marca
sǎ aparǎ la aruncarea a doua. Sǎ se determine:
a)
spatiul ![]() al probelor,
al probelor,
b) probele
care favorizeazǎ respectiv aparitiile
evenimentelor ![]() ,
, ![]() si
si ![]() ,
,
c) evenimentele
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
d) probabilitǎtile evenimentelor de la punctele precedente.
Rǎspunsuri.a) ![]() ; d)
; d) ![]()
![]()
![]()
![]()
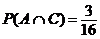
![]()
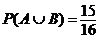
![]()
![]()
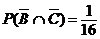
![]()
![]()
![]()
![]()
![]()
2.
Un client cumpǎrǎ
dintr-un magazin patru articole de imbrǎcǎminte. Fie ![]() ,
, ![]() ,
, ![]() ,
, ![]() respectiv evenimentele
ca primul, al doilea, al treilea si al patrulea articol sǎ nu continǎ defectiuni. Sǎ se exprime cu
ajutorul acestor evenimente, urmǎtoarele evenimente:
respectiv evenimentele
ca primul, al doilea, al treilea si al patrulea articol sǎ nu continǎ defectiuni. Sǎ se exprime cu
ajutorul acestor evenimente, urmǎtoarele evenimente:
a) nici un articol nu prezintǎ defectiuni,
b) cel putin un articol prezintǎ defectiuni,
c) exact un articol prezintǎ defectiuni,
d) exact douǎ articole prezintǎ defectiuni,
e) cel mult douǎ articole prezintǎ defectiuni.
Rǎspunsuri. a) ![]() ; b)
; b) ![]() ;
;
c) ![]() ;
;
d) ![]()
e)
![]()
3. Un lacǎt are un cifru format din patru cifre. Sǎ se calculeze pobabilitatea de a ghici cifrul lacǎtului dacǎ:
a) lacǎtul functioneazǎ perfect,
b) ultima cifrǎ, din cauza unei defectiuni nu trebuie sǎ coincidǎ cu ultima cifrǎ a combinatiei considerate,
c) prima si ultima cifrǎ nu trebuie sǎ coincidǎ cu prima respectiv ultima cifrǎ a combinatiei considerate.
Rǎspunsuri. a) ![]() ; b)
; b) ![]() ; c)
; c) ![]() .
.
4. La o conferintǎ de presǎ participǎ 7 ziaristi strǎini si 17 ziaristi autohtoni(8 femei si 9 bǎrbati). stiind cǎ la conferinta de presǎ vor pune intrebǎri 6 ziaristi luati la intamplare din cei 24 prezenti, se cere probabilitatea ca intrebǎrile sǎ fie puse de:
a) 2 ziaristi strǎini si 4 autohtoni;
b) 2 ziaristi strǎini si 4 autohtoni(2 femei si 2 bǎrbati);
c) 1 ziarist strǎin si 5 autohtoni (2 femei si 3 bǎrbǎti).
Rǎspunsuri. a) ![]() ; b)
; b) ![]() ; c)
; c) ![]() .
.
5. Piesele produse de o masinǎ prezintǎ rebut in procente 2%. Pentru controlul calitǎtii produselor, se iau la intǎmplare 10 piese. Sǎ se calculeze probabilitatea ca:
a) nici o piesǎ sǎ nu fie defectǎ,
b) cel mult douǎ piese sǎ fie defecte.
Rǎspunsuri. a)![]()
b)![]()
6. Se stie cǎ un magazin de cosmetice are acelasi numǎr de clienti bǎrbati, respectiv femee. Se considerǎ primii 12 clienti ai magazinului dintr-o zi fixatǎ. Sǎ se calculeze probabilitatea ca 12 dintre cei 12 clienti:
a) patru sǎ fie femei,
b) sǎ fie cel mult patru femei.
Rǎspunsuri. a)![]() ;
;
b)![]() .
.
Se aruncǎ un zar de 15 ori. Sǎ se calculeze probabilitatea ca de 5 ori sǎ aparǎ numǎr prim, de 8 ori sǎ aparǎ numǎr compus si de 2 ori sǎ aparǎ fata cu un punct.
Rǎspuns. ![]() .
.
8. La o loterie s-au vandut 85 bilete loto, din care o persoanǎ a cumpǎrat 10 bilete. Stiind cǎ din cele 85 bilete trei sunt castigǎtoare, sǎ se calculeze probabilitatea ca persoana care a cumpǎrat cele 10 bilete:
a) sǎ nu fi castigat,
b) sǎ aibǎ un bilet castigǎtor,
c) sǎ aibǎ cel putin un bilet castigǎtor.
Rǎspunsuri. a)![]() ; b)
; b) ![]()
c)![]()
9. Intr-un magazin cu autoservire, pe un raft se aflǎ cate 10 ciocolate care costǎ respectiv 1 mie lei, 3 mii de lei, 5 mii de lei si 10 mii de lei. O persoanǎ ia la intamplare 5 ciocolate. Sǎ se determine probabilitatea ca suma plǎtitǎ sǎ fie 25 mii de lei.
Rǎspuns. ![]() .
.
10. Se aruncǎ cinci zaruri, dintre care unul are o fatǎ coloratǎ in alb si celelalte in negru, altul are douǎ fete colorate in alb si celelalte in negru, altul are trei fete colorate In alb si celelalte in negru, altul are patru fete colorate in alb si celelalte in negru, iar altul are cinci fete colorate in alb si celelalte in negru. Sǎ se calculeze probabilitatea:
a) sǎ se obtinǎ pe trei din cele cinci zaruri culoarea albǎ,
b) sǎ se obtinǎ cel putin pe douǎ zaruri culoarea albǎ.
Rǎspunsuri. a) ![]() ;
;
b) ![]() , unde
, unde ![]() si
si ![]() ,
, ![]() .
.
11. Se stie cǎ 3 din patru clienti care intrǎ intr-o unitate alimentarǎ fac cumpǎrǎturi de la unitatea respectivǎ. Sǎ se calculeze probabilitatea ca:
a) primul cumpǎrǎtor sǎ aparǎ dupǎ trei clienti carea au pǎrǎsit magazinul fǎrǎ sǎ cumpere nimic din unitatea respectivǎ,
b) panǎ la al doilea cumpǎrǎtor doi clienti sǎ nu fi efectuat cumpǎrǎturi.
Rǎspunsuri. a)![]() ; b)
; b) ![]() .
.
12. Zece
aparate de acelasi tip sunt date in folosinta , trei provenind de la
unitatea ![]() , cinci de la unitatea
, cinci de la unitatea ![]() , iar douǎ de la unitatea
, iar douǎ de la unitatea ![]() . Se supun aceste aparate unei probe de verificare. Cele care
provin de la unitatea
. Se supun aceste aparate unei probe de verificare. Cele care
provin de la unitatea ![]() trec proba cu
probabilitate de 0,9, cele de la
trec proba cu
probabilitate de 0,9, cele de la ![]() cu probabilitatea
0,75, iar cele de la
cu probabilitatea
0,75, iar cele de la ![]() cu probabilitatea
0,85. Se ia un aparat la intamplare si se cere probabilitatea ca:
cu probabilitatea
0,85. Se ia un aparat la intamplare si se cere probabilitatea ca:
a) aparatul sǎ treacǎ proba de verificare,
b)
aparatul sǎ provinǎ de la unitatea ![]() dacǎ se stie cǎ a trecut
proba de verificare.
dacǎ se stie cǎ a trecut
proba de verificare.
Rǎspunsuri. a) ![]() ;
; 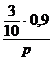 .
.
13. Consumul
zilnic de energie electricǎ intr-o unitate comercialǎ este normal cu
probabilitatea ![]() . Fie
. Fie ![]() numǎrul zilelor
din sǎptǎmanǎ cand consumul este normal. Sǎ se scrie
distributia variabilei
aleatoare
numǎrul zilelor
din sǎptǎmanǎ cand consumul este normal. Sǎ se scrie
distributia variabilei
aleatoare ![]()
Rǎspuns. 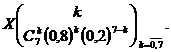
14. Se
aruncǎ o monedǎ de trei ori. Se noteazǎ cu ![]() si
si ![]() respectiv numǎrul
aparitiilor mǎrcii
in cele trei aruncǎri si numǎrul
de mǎrci consecutive apǎrute in cele trei aruncǎri. Sǎ se
scrie distributiile:
respectiv numǎrul
aparitiilor mǎrcii
in cele trei aruncǎri si numǎrul
de mǎrci consecutive apǎrute in cele trei aruncǎri. Sǎ se
scrie distributiile:
a) variabilelor aleatoare ![]() si
si ![]() ,
,
b) vectorului
aleator ![]() ,
,
c) variabilelor
aleatoare ![]() si
si ![]() .
.
Rǎspunsuri. a) 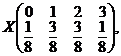 respectiv
respectiv 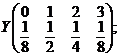
b)

c)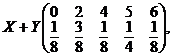
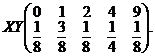
15. La o librǎrie s-au primit 10 exemplare dintr-o
carte, din care 4 prezintǎ mici defectiuni. Trei cumpǎrǎtori iau la intamplare cate o
carte din cele 10. Fie ![]() numǎrul cǎrtilor cu defectiuni vandute celor trei
cumpǎrǎtori. Sǎ se scrie distributia variabilei aleatoare
numǎrul cǎrtilor cu defectiuni vandute celor trei
cumpǎrǎtori. Sǎ se scrie distributia variabilei aleatoare ![]() si functia
de repartitie corespunzǎtoare variabilei aleatoare
si functia
de repartitie corespunzǎtoare variabilei aleatoare ![]() , iar apoi sǎ se reprezinte grafic functia de repartitie.
, iar apoi sǎ se reprezinte grafic functia de repartitie.
Rǎspuns. Legea
hipergeometricǎ: 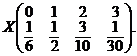
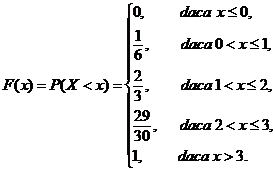
16. O persoanǎ cumpǎrǎ pe rand bilete loz
in plic panǎ cand obtine un bilet castigǎtor. Stiind
cǎ un bilet este castigǎtor cu probabilitatea ![]() si notand cu
si notand cu ![]() numǎrul biletelor
necastigǎtoare cumpǎrate, sǎ se scrie distributia variabilei aleatoare
numǎrul biletelor
necastigǎtoare cumpǎrate, sǎ se scrie distributia variabilei aleatoare ![]() si functia
repartitie atasatǎ variabilei aleatoare
si functia
repartitie atasatǎ variabilei aleatoare ![]() .
.
Rǎspuns. 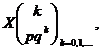
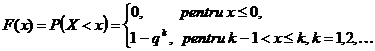
1 Variabila
aleatoare ![]() de tip continuu are
densitatea de probabilitate
de tip continuu are
densitatea de probabilitate
![]()
unde ![]() este o constantǎ
realǎ. Sǎ se determine:
este o constantǎ
realǎ. Sǎ se determine:
a) constanta
realǎ ![]() ,
,
b) functia de repartitie corespunzǎtoare,
c) probabilitǎtile ![]() si
si ![]()
Rǎspunsuri. a)![]() ; b)
; b)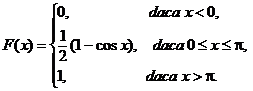
c) 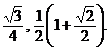
18. Se
considerǎ vectorul aleator ![]() cu densitatea de
probabilitate
cu densitatea de
probabilitate
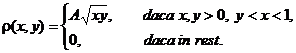
Sǎ se determine:
a)
constanta realǎ ![]()
b)
densitǎtile de probabilitate ![]() si
respectiv
si
respectiv ![]() pentru
variabilele aleatoare
pentru
variabilele aleatoare ![]() si
si ![]()
c)
probabilitǎtile ![]() si
si ![]()
Rǎspunsuri. a) ![]()
b) 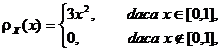
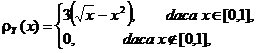
c) ![]()
19. Variabila
aleatoare ![]() urmeazǎ
legea normalǎ
urmeazǎ
legea normalǎ ![]() Sǎ se determine
densitǎtile de probabilitate respectiv variabilele aleatoare
Sǎ se determine
densitǎtile de probabilitate respectiv variabilele aleatoare ![]() si
si ![]()
Rǎspuns. 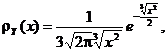
![]()
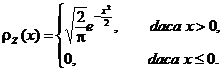
20. O
persoanǎ doreste sǎ
deschidǎ un lacǎt si are ![]() chei, dintre care
numai una se potriveste. Pentru aceasta, incearcǎ la intamplare
deschiderea lacǎtului cu aceste chei. Fie
chei, dintre care
numai una se potriveste. Pentru aceasta, incearcǎ la intamplare
deschiderea lacǎtului cu aceste chei. Fie ![]() numǎrul de
incercǎri efectuate pentru deschiderea lacǎtului. Sǎ se scrie
distributia variabilei
aleatoare
numǎrul de
incercǎri efectuate pentru deschiderea lacǎtului. Sǎ se scrie
distributia variabilei
aleatoare ![]() , iar apoi sǎ se calculeze valoarea medie si
dispersia variabilei aleatoare
, iar apoi sǎ se calculeze valoarea medie si
dispersia variabilei aleatoare ![]() , dacǎ:
, dacǎ:
a) cheile incercate se pun impreunǎ cu celelalte,
b) cheile incercate se inlǎturǎ.
Rǎspunsuri. a)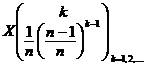
![]()
![]()
b) 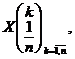
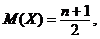
![]()
21. La patru
unitǎti alimentare din oras se poate gǎsi zilnic paine
proaspǎtǎ cu probabilitǎtile ![]() ,
, ![]() ,
, ![]() si respectiv
si respectiv ![]() Fie
Fie ![]() numǎrul
unitǎtilor alimentare din cele patru la care se gǎseste paine proaspǎtǎ intr-o
zi fixatǎ. Sǎ se determine:
numǎrul
unitǎtilor alimentare din cele patru la care se gǎseste paine proaspǎtǎ intr-o
zi fixatǎ. Sǎ se determine:
a)
distributia variabilei aleatoare ![]() ,
,
b)
valoarea medie,
dispersia, abaterea medie pǎtraticǎ, mediana si modul variabilei aleatoare ![]() .
.
Rǎspunsuri. a)![]()
b) ![]()
![]()
![]()
![]()
22. Fie ![]() coordonatele unui
punct luminos ce reprezintǎ o tintǎ pe
un ecran radar circular si care urmeazǎ legea uniformǎ pe
domeniul
coordonatele unui
punct luminos ce reprezintǎ o tintǎ pe
un ecran radar circular si care urmeazǎ legea uniformǎ pe
domeniul ![]() Sǎ se determine
valoarea medie si dispersia
distantei
Sǎ se determine
valoarea medie si dispersia
distantei ![]() de la centrul
ecranului panǎ punctul luminos.
de la centrul
ecranului panǎ punctul luminos.
Rǎpuns. ![]()
![]()
23.
Variabila aleatoare ![]() urmeazǎ legea
beta. Sǎ se calculeze momentele initiale, iar apoi valoarea medie,
dispersia si abaterea medie pǎtraticǎ a variabilei aleatoare
urmeazǎ legea
beta. Sǎ se calculeze momentele initiale, iar apoi valoarea medie,
dispersia si abaterea medie pǎtraticǎ a variabilei aleatoare ![]() .
.
Rǎspuns. ![]()
![]()
![]()
![]()
24. Fie
punctul ![]() fixat si punctul
aleator
fixat si punctul
aleator ![]() care urmeazǎ
legea uniformǎ pe intervalul
care urmeazǎ
legea uniformǎ pe intervalul ![]() Sǎ se
determine corelatia dintre
Sǎ se
determine corelatia dintre ![]() si distanta
si distanta ![]() de la
de la ![]() la
la ![]() , iar apoi sǎ se determine valoarea lui
, iar apoi sǎ se determine valoarea lui ![]() pentru care
variabilele aleatoare
pentru care
variabilele aleatoare ![]() si
si ![]() sunt necorelate.
sunt necorelate.
Rǎspuns. ![]()
25. Folosind inegalitatea lui Cebisev, sǎ se arate cǎ
![]()
dacǎ variabila
aleatoare ![]() are densitatea de
probabilitate
are densitatea de
probabilitate
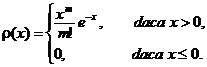
Rǎspuns. ![]()
26.
Probabilitatea ca o persoanǎ sǎ gǎseascǎ loc la un hotel
este ![]() In decursul unei luni
de zile, la hotelul respectiv s-au prezentat 4000 de persoane. Fie
In decursul unei luni
de zile, la hotelul respectiv s-au prezentat 4000 de persoane. Fie ![]() numǎrul
persoanelor care au gǎsit loc la hotel din totalul de 4000. Sǎ se
determine probabilitatea ca:
numǎrul
persoanelor care au gǎsit loc la hotel din totalul de 4000. Sǎ se
determine probabilitatea ca:
a) numǎrul persoanelor care au gǎsit loc la hotel sǎ fie cuprins intre 3000 si 3400,
b) numǎrul persoanelor care au gǎsit loc la hotel sǎ nu depǎseascǎ pe 3000,
c) numǎrul persoanelor care nu au gǎsit loc la hotel sǎ fie mai mic decat 500.
Rǎspunsuri. a) ![]() (inegalitatea lui Cebisev),
(inegalitatea lui Cebisev), ![]() (teorema lui
Moivre-Laplace); b)
(teorema lui
Moivre-Laplace); b) ![]() (teorema
Moivre-Laplace); c)
(teorema
Moivre-Laplace); c) ![]() (teorema
Moivre-Laplace).
(teorema
Moivre-Laplace).
2 Probabilitatea
ca o persoanǎ sǎ fie admisǎ la examenul de sofer amator este ![]() Intr-o lunǎ se
prezintǎ un numǎr de
Intr-o lunǎ se
prezintǎ un numǎr de ![]() candidati la
acest examen. Sǎ se determine numǎrul
candidati la
acest examen. Sǎ se determine numǎrul ![]() astfel incat sǎ
putem afirma cu o probabilitate de cel putin 0,95 cǎ frecventa relativǎ a
promovatilor sǎ se abatǎ de la probabilitatea
astfel incat sǎ
putem afirma cu o probabilitate de cel putin 0,95 cǎ frecventa relativǎ a
promovatilor sǎ se abatǎ de la probabilitatea ![]() mai putin de
0,01, utilizand atat inegalitatea lui Cebisev, cat si teorema
Moivre-Laplace.
mai putin de
0,01, utilizand atat inegalitatea lui Cebisev, cat si teorema
Moivre-Laplace.
Rǎspuns. ![]() (inegalitatea lui
Cebisev),
(inegalitatea lui
Cebisev), ![]() (teorema
Moivre-Laplace).
(teorema
Moivre-Laplace).
28. Probabilitatea ca o
piesǎ luatǎ la intamplare sǎ fie defectǎ este ![]() Sunt testate 100 de
piese. Sǎ se evalueze probabilitatea ca:
Sunt testate 100 de
piese. Sǎ se evalueze probabilitatea ca:
a) cel putin 5 piese sǎ fie defecte,
b) mai putin de 5 piese sǎ fie defecte,
c) numǎrul pieselor defecte sǎ fie cuprins intre 5 si 10.
Rǎspunsuri. a) ![]() (teorema
Moivre-Laplace);
(teorema
Moivre-Laplace);
b) ![]() (teorema
Moivre-Laplace);
(teorema
Moivre-Laplace);
c) ![]() (teorema
Moivre-Laplace).
(teorema
Moivre-Laplace).
29. Probabilitatea
ca o piesǎ luatǎ la intamplare sǎ fie defectǎ este ![]() Un lot de piese este
respins dacǎ contine cel
putin 10 piese defecte. Sǎ se determine numǎrul de piese ce
trebuie testate pentru ca un lot sǎ fie respins cu probabilitatea 0,8
Un lot de piese este
respins dacǎ contine cel
putin 10 piese defecte. Sǎ se determine numǎrul de piese ce
trebuie testate pentru ca un lot sǎ fie respins cu probabilitatea 0,8
Rǎspuns. ![]() (teorema
Moivre-Laplace).
(teorema
Moivre-Laplace).
30. Sǎ
se arate cǎ sirul ![]() de variabile aleatoare
independente, care au distributiile
de variabile aleatoare
independente, care au distributiile
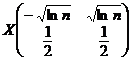
urmeazǎ legea numerelor mari.
Rǎspuns. Se aplicǎ teorema lui Markov.
![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2999
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved