STABILITATEA EXCAVATIILOR SUBTERANE DIN SALINE

Verificarea stabilitatii excavatiilor din saline trebuie orientata spre stabilirea dimensiunilor camerelor, a pilierilor si a planseelor, respectiv spre cunoasterea rezervei de stabilitate.

Prin notiunea de stabilitate se defineste o asemenea stare a sistemului, care mentine un echilibru sigur si durabil al acestuia, cu pastrarea sectiunii de lucrare a excavatiei subterane pe intreaga durata de folosire a acesteia.

Evaluarea stabilitatii unei excavatii subterane se face pe baza unor calcule, folosind metode clasice sau numerice.

Indiferent de metoda aleasa, in vederea realizarii unor calcule de stabilitate trebuie sa se urmareasca:

caracteristicile geomecanice ale substantei minerale utile - sarea - si ale rocilor acoperitoare;

metoda de exploatare aplicata si procesul de derocare - manual, taieri mecanizate, cu explozivi, combinat etc.

functia pe care o indeplineste excavatia subterana su durata de folosire - exploatare - a acesteia.

Daca aceste etape au fost parcurse, se poate trece la verificarea stabilitatii camerelor, a pilierilor si a planseelor.

EVALUAREA STABILITATII EXCAVATIILOR DIN MINELE DE SARE PE BAZA METODELOR CLASICE DE CALCUL

VERIFICAREA STABILITATII CAMERELOR

In minele de sare din Romania camerele de exploatare au forma de colpot, forma trapezoidala continuata cu forma dreptunghiulara si mai frecvent forma dreptunghiulara.

Forma si dimensiunile acestor camere in general este prezentata in cap.1 din [6].

Deschiderea la tavan a camerelor

Din numeroasele metode de determinare a deschiderii la tavan, respectiv a latimii camerelor, aici vom aborda doua procedee care si-au gasit o aplicabilitate practica.

PROCEDEUL RITTER

Acest procedeu se bazeaza pe studiul presiunii care actioneaza asupra tavanului unei excavatii subterane, executate intr-o roca sau o substanta minerala utila, cu caracteristici preponderent elastice omogene si izotrope [13], [27], [28], [30].

Autorul considera ca, in conformitate cu aceasta ipoteza, greutatea rocilor care se gasesc deasupra excavatiei si care sunt cuprinse in interiorul unei bolti de echilibru (Q), trebuie sa fie echilibrata de rezultanta componentelor verticale (D) ale fortelor de coeziune ale rocii sau substantei minerale utile, forte care se manifesta ca niste rezistente la tractiune care actioneaza de-a lungul boltii de echilibru, fig.5.1.

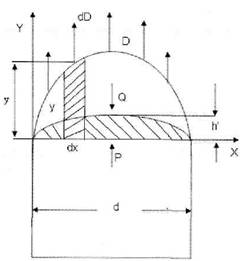
Fig.5.1. Schema de calcul a presiunii dupa W.Ritter

Scriind aceasta conditie de echilibru se ajunge la relatia:

sau:

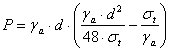[MPa], unde:

- greutatea specifica aparenta a rocii sau a substantei minerale utile in care s-a executat excavatia subterana; - in cazul nostru sarea gema -

d - deschiderea la tavan sau latimea camerei;

- rezistenta de rupere la tractiune a rocii sau substantei minerale utile (pe esantion).

Daca se noteaza:

Inlocuind rezulta:

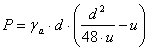[MPa]

Deschiderea maxima rezulta din conditia:

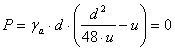
De aici: sau

In tabel 5.1. se arata variatia presiunii asupra tavanului in functie de deschiderea camerei.

Tabel 5.1.Variatia presiunii "P" in functie de deschiderea "d"

Din tabel 5.1. rezulta ca deschiderea optima a camerelor este:

sau [m]

Pentru cazul in care, din motive tehnice, camerele au [m], inaltimea de boltire a camerelor rezulta din:

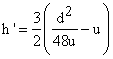[m]

Pentru cazul minei Cocenesti - Valcea si pentru un coeficient de siguranta n = 5, rezulta:

[m]

Dupa cum, camerele dreptunghiulare au latimea de 16 m si inaltimea de 8 m, rezulta ca acestea sunt stabile din punct de vedere a deschiderii lor.

De fapt coeficientul de siguranta real este:

Rezulta ca, rezerva de stabilitate a camerelor din acest punct de vedere este foarte mare.

PROCEDEUL LUI M.M. PROTODIAKONOV

Ca si procedeul lui W. Ritter, procedeul de calcul al deschiderii la tavan a camerelor al lui M.M. Protodiakonov are la baza tot marimea presiunii care actioneaza asupra tavanului camerei de exploatare cu diferenta ca aici, roca sau substanta minerala utila este considerata omogena, fara coeziune, fig.5.2. [13], [27], [28].

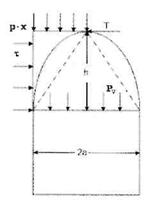
Fig.5.2. Schema de calcul a presiunii dupa M.M. Protodiakonov

In acest caz:

a - semideschiderea lucrarii sau camerei de exploatare, m;

f - coeficientul de tarie a rocii sau a substantei minerale utile dupa clasificarea lui M.M.Protodiakonov.

Lungimea arcului de parabola - care se formeaza in tavanul excavatiei - si pentru cazul cand este dat de relatia:

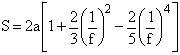
Rezistenta la tractiune a rocilor dupa bolta parabolica va fi:

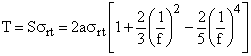
Punand conditia ca greutatea rocilor care se afla in interiorul boltii parabolice sa fie echilibrata de forta la tractiune dupa bolta parabolica, rezulta:

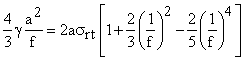
De aici, pentru (pentru sare se poate considera daN/cm²), rezulta:

[m] Se observa ca, daca se compara cele doua procedee- W.Ritter si M.M.Protodiakonov care pornesc de la premize diferite - mediu elastic in primul caz si mediu fara coeziune in al doilea caz - se ajunge la rezultate apropiate din punct de vedere tehnic, procedeul PROTODIAKONOV prezentand o rezerva de stabilitate si mai mare decat procedeul RITTER.

Calculul lungimii unei camere

Punand conditia ca peretii unei camere de exploatare sa nu se prabuseasca sub greutatea rocilor acoperitoare, H. Borger [13], [27], [28], [30] ajunge la relatia:

in care:

- rezistenta limita la forfecare, pe conturul camerei de exploatare;

- greutatea sarii/rocilor pana la suprafata, care actioneaza asupra camerei de exploatare;

- rezistenta la forfecare rocii sau substantei minerale utile din pereti; - sare -

H - adancimea la care se afla camera fata de suprafata;

deschiderea (latimea) camerei;

L - lungimea camerei.

Din aceasta relatie se ajunge la:

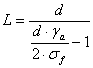[m]

unde:

Prima constatare este aceea ca, lungimea camerelor de exploatare nu este dependenta de adancime.

Daca pentru sarea gema de la Cocenesti vom admite valorile din tabelul 3.20:

N/m³

N/m²

n = 5

Obtinem:

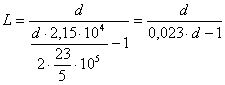
Pentru m, rezulta L → ∞.

Cu alte cuvinte, pentru orice valoare a deschiderii la tavan d ≤ 43 m, lungimea camerelor poate fi infinita - Cazul Cocenesti -

Calculul inaltimii camerei

Minele vechi de sare din Romania au fost exploatate prin metoda camerelor sub forma de clopot, a camerelor trapezoidale continuate cu camere dreptunghiulare cu pereti drepti, cu camere trapezoidale si cu camere dreptunghiulare.

Deoarece, la mina Cocenesti, la cele doua orizonturi 210 si 226, se aplica metoda de exploatare cu camere si pilieri patrati - camere care au latimea de 15 - 16 m si inaltimea de 8 m - rezulta ca avem de a face cu camere dreptunghiulare.

Tinand seama de faptul ca si stabilitatea camerelor cu profil dreptunghiular se deduce din stabilitatea camerelor cu profil trapezo-dreptunghiular, ne vom ocupa in primul rand de stabilitatea acestor camere.

a. Camere cu profil trapezoidal, continuate cu profil dreptunghiular (pereti verticali) - camere trapezo-dreptunghiulare -

Asa cum s-a aratat in introducerea acestui paragraf, camerele trapezoidale continuate in adancime cu camere dreptunghiulare au fost introduse in perioada imediat urmatoare renuntarii la camerele de tip clopot. Aceste camere reprezinta un insemnat potential balnear, turistic sau economic cu conditia ca acestea sa fie stabile.

Pentru determinarea inaltimii maxime "h" a partii din camera care are peretii verticali se va aplica ipoteza C. Coulomb - G. Rebhann (ipoteza I - a de calcul) punand conditia ca presiunea exercitata de masa de sare perpendiculara pe unul din pereti sa fie egala, la limita, cu rezistenta la tractiune a sarii pe suprafata pe care actioneaza presiunea (fig. 5.3). Cu aceasta conditie, rezulta: [12], [27].

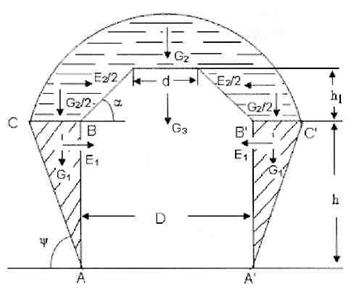
Fig.5.3. Schema de calcul a inaltimii "h" a camerei in ipoteza I - a de calcul

Pe langa semnificatiile din fig. 5.3 avem:

φ - unghiul de frecare interioara.

Pentru (sarea de la Cocenesti) → tabel 3.20 rezulta:

Inlocuind valorile lui D, h₁, α si , rezulta o ecuatie de gradul 3 de forma:

sau:

Daca:

rezulta:

Notam: si inlocuind rezulta:

Daca:

Ecuatia va avea o radacina reala si doua radacini complex conjugate. Acest tip de ecuatie poate fi rezolvata prin metoda CARDAN.

Daca:

Acesta este cazul ireductibil si el poate fi rezolvat cu ajutorul functiilor circulare si hiperbolice.

Ipoteza a II-a de calcul, nu este foarte diferita de prima ipoteza de calcul.

In esenta, a II-a ipoteza considera ca, datorita presiunii create de bolta parabolica de echilibru natural asupra tavanului si asupra peretilor la o anumita inaltime a camerei se produce alunecarea peretilor dupa suprafetele inclinate cu unghiul (fig.5.4).

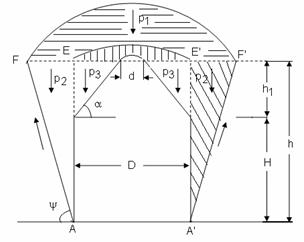
Fig.5.4. Schema de calcul a inaltimii camerei dupa a II-a ipoteza de calcul

Asupra acestor prisme triunghiulare, (fig.5.4) actioneaza urmatoarele solicitari:

Pentru echilibru, este necesar ca toate aceste solicitari sa fie egale cu tensiunea de rupere la forfecare dupa suprafata .

Explicitand relatia anterioara rezulta:

Daca atunci:

Inlocuind, rezulta:

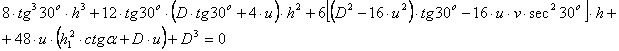
Inlocuind valorile lui D; h₁; α si , respectiv se ajunge la o relatie de forma ecuatiei de gradul III, de unde mersul calculului este similar ca si in cazul precedent.

Asa cum am aratat mai inainte, diferentele care rezulta lucrand cu prima ipoteza sau cu ipoteza a II-a sunt relativ mici astfel incat poate fi acceptata oricare din cele doua ipoteze. Practica arata ca, ipoteza a II-a da rezultatele cele mai bune.

b. Camere cu profil dreptunghiular

Camerele cu profil dreptunghiular sunt un caz particular al camerelor cu profil trapezoidal continuate cu pereti verticali.

Astfel, pornind de la relatia principala - ipoteza a II-a - si facand si , rezulta:

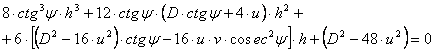
Pentru

Rezulta:

Radacinile ecuatiei sunt:

h₁ = 0

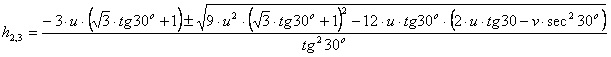
Cunoscand valorile si acceptand un anumit coeficient de siguranta "n", calculam:

,

Inlocuind aceste valori in ecuatia de mai sus rezulta valoarea inaltimii maxime a camerelor cu profil dreptunghiular.

Astfel, luand in considerare datele din tabelul 3.20 rezulta pentru n = 4:

u = 14 iar v = 26,7.

Cu aceste date, h30 m.

Sigur ca, aceasta inaltime este mult mai mare decat inaltimea reala a camerei care este de 8 m.

Coeficientul de siguranta real, care stabileste rezerva de stabilitate se determina din ecuatia de baza si are forma:

, unde:

; ; iar

Inlocuind rezulta:

A = 251; B = 3930 iar n = 14,7.

Rezulta de aici ca rezerva de stabilitate a camerei - luand in considerare inaltimea acesteia - este foarte mare, deci camera este stabila.

STABILITATEA PILIERILOR

Toti cercetatorii care s-au ocupat de problema dimensionarii pilierilor (inclusiv la minele de sare) sunt de acord ca asupra stalpilor (pilierilor) dintre camere actioneaza tensiuni statice de compresiune datorate propriei greutati si a greutatii unei anumite parti din rocile acoperitoare [6], [13], [28], [30].

In consecinta, pentru stabilirea dimensiunilor optime pe care trebuie sa le aiba pilierii, trebuie sa se cunoasca:

rezistentele mecanice ale substantei minerale utile din pilieri;

felul, marimea si modul de repartizare a tensiunilor din interiorul acestora;

marimea deformatiilor pe care le sufera pilierii.

Respectand mai mult sau mai putin aceste principii, au fost create de-a lungul timpului o serie intreaga de procedee de dimensionare si verificare, dupa cum urmeaza:

Procedee bazate pe ipoteza repartitiei uniforme a tensiunilor in stalpi si a rezistentei constante la compresiune (Tournaire, Goupilliere, Gruner, Seviakov);

Procedee bazate pe ipoteza repartitiei uniforme a tensiunilor in stalpi si a rezistentei la compresiune variabile, functie de forma si dimensiunile stalpilor (Kegel, Stamatiu, Ruppeneit, Koshling);

Procedeele bazate pe ipoteza repartitiei neuniforme a tensiunilor si a parabolei de presiune (Protodiakonov, Slesarev, Stamatiu);

Procedee bazate pe teoria elasticitatii (Timbarevici, Ruppeneit).

In cuprinsul prezentei lucrari, ne propunem sa facem o verificare dupa cateva metodologii care au fost confirmate in practica.

Procedeul de calcul al dimensionarii pilierilor propus de academicianul I.D. Seviakov

L.D.Seviakov a examinat in mod detaliat problema dimensionarii stalpilor de sustinere de la exploatarile subterane si a propus o serie de formule de calcul pentru stalpi de diferite forme, fig. 5.5.

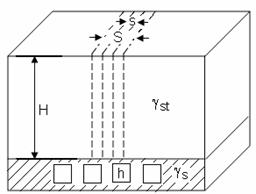
Fig.5.5. Schema de calcul a latimii pilierilor dupa L.D. Seviakov

Aceste formule se bazeaza pe admiterea urmatoarelor ipoteze:

a) Cea mai redusa sarcina posibila asupra stalpilor de sustinere este conditionata de greutatea tuturor rocilor acoperitoare pana la suprafata;

b) Tensiunile verticale de compresiune in sectiunile orizontale ale stalpilor vor fi considerate ca uniform repartizate, presupunandu-se ca inegalitatea reala de repartizare a eforturilor verticale in stalp se compenseaza cu rezerva de rezistenta ce se introduce in calcule;

c) In calcule se introduc rezistentele de rupere la compresiune ale rocilor, obtinute prin incercari de laborator, cu corectivele in ceea ce priveste forma stalpilor.

d) Neluarea in considerare a unei oarecare cresteri a rezistentei, in cazul cresterii dimensiunilor absolute ale epruvetelor, a rezistentei mai mari la compresiune a stalpilor a caror inaltime este mai mica decat dimensiunile bazei lor, precum si a rezistentei mai mari a materialului respectiv in cazul compresiunii pe doua axe in comparatie cu aceea pe o axa care introduce in calcule, pentru cazurile corespunzatoare, o oarecare rezerva de rezistenta.

Notandu-se cu:

H - adancimea partii superioare a stalpului de sustinere fata de suprafata, m;

h - inaltimea stalpului de sustinere, m ;

s - suprafata sectiunii orizontale a stalpului de sustinere, m² ;

S - suprafata sectiunii orizontale a prismei de roci acoperitoare ce revine unui stalp de sustinere, m²;

si - latimea camerelor care inconjoara stalpii de sustinere, m;

latimea stalpului de sustinere, m;

- greutatea specifica aparenta medie a rocilor acoperitoare, N/m³;

- greutatea specifica aparenta medie a materialului din stalpii de sustinere, N/m³

- rezistenta medie efectiva de rupere la compresiune din stalpii de sustinere, determinata pe cuburi cu muchiile de 5 - 20 cm, MPa;

n - coeficient de siguranta, reprezentand rezerva de rezistenta la calculul stalpilor de sustinere (n = 2 3 pentru sarea gema si sarurile de potasiu).

Tinand seama de conditiile ce decurg din ipotezele mentionate, L.D.Seviakov a dedus urmatoarea relatie generala pentru calculul dimensiunilor admisibile ale stalpilor de sustinere:

de unde rezulta pentru cazul limita:

Pe baza acestei relatii generale s-au stabilit urmatoarele formule de calcul a latimii stalpilor de sustinere:

I. Stalpi (pilieri) lungi (continui)

Pentru acesti stalpi, considerand o portiune cu lungimea egala cu unitatea, avem:

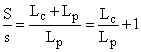unde

de unde rezulta:

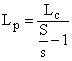
sau, tinand seama de relatia anterioara:

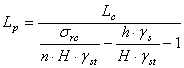[m]

II. Stalpi (pilieri) scurti cu sectiunea patrata

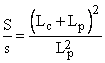
de unde rezulta:

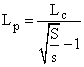
sau, tinand seama de relatia S/s, rezulta:

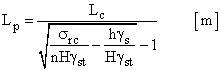
Si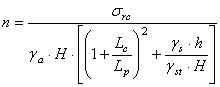

III. Stalpi (pilieri) scurti cu sectiune dreptunghiulara inconjurati de camere cu latime constanta

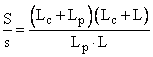
de unde rezulta:

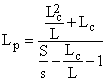
sau tinand seama de relatia S/s, rezulta:

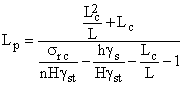[m]

IV. Stalpi (pilieri) scurti cu sectiune dreptunghiulara inconjurati de camere cu latimi diferite

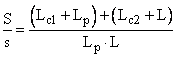si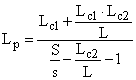

de unde rezulta tinand seama de relatia S/s:

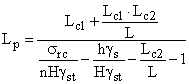[m]

Formulele stabilite de L.D.Seviakov se bazeaza pe ipoteza de calcul admisa de Tournaire, in ceea ce priveste marimea eforturilor verticale care actioneaza asupra stalpilor de sustinere.

Cat priveste marimea rezistentei de rupere la compresiune a materialului din stalpi, care intra in formulele de calcul, aceasta este considerata ca o marime constanta pentru acelasi material, fiind determinata prin incercari de laborator pe cuburi avand latura de 5 - 20 cm si afectata de un coeficient de siguranta n.

Aceste relatii au avantajul fata de relatiile stabilite de Tournaire, Coupiliere si Gruner, ca permit calculul direct al latimii stalpilor (pilierilor) de sustinere si nu verificarea unor dimensiuni prealabil alese ale acestora.

Relatiile de calcul ale dimensiunii pilierilor de sustinere, propuse de L.D.Seviakov, prezinta dezavantajul ca, deoarece rezistenta de rupere la compresiune a materialului din stalp (pilier) este considerata constanta pentru acelasi material, iar coeficientul de siguranta luat arbitrar, dimensiunile deduse nu satisfac complet conditiile optime de dimensionare a pilierilor.

Pentru aplicarea relatiilor stabilite de SEVIAKOV in conditiile - Cocenesti-Valcea - trebuie sa precizam conditiile reale ale aplicarii metodei de exploatare cu camere si pilieri scurti.

Astfel, exploatarea primului orizont - turism - se gaseste la o adancime fata de suprafata de 100 m, din care 50 m roca sterila cu N/m³ si 50 m sare cu N/m³.

In acest caz, greutatea specifica aparenta medie a rocilor acoperitoare va fi:

N/m³

Pentru L_c = 15 m si n = 2, rezulta:

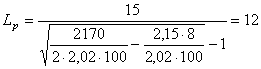m

Dupa cum, pilierii au latimea de 15 m, rezulta ca este indeplinita conditia de stabilitate cu un coeficient de siguranta real, n = 2,63.

Metoda de dimensionare a pilierilor propusa de Sokolovsky - Ruppeneit

Dupa cum s-a mentionat in prima parte a acestui capitol, din punct de vedere al sigurantei si stabilitatii, stalpii de sustinere (pilierii) trebuie sa satisfaca, asa cum s-a mai aratat, anumite conditii de rezistenta si deformare. Astfel, tensiunile existente in pilieri datorita sarcinii efective la care sunt solicitati trebuie sa fie inferioare rezistentei de rupere a materialului din pilier, cu satisfacerea conditiei .

n - este coeficientul de siguranta adoptat, iar deformatiile sa fie cat mai mici, elastice sau plastice mici.

O prima problema, care se cere solutionata pentru estimarea stabilitatii pilierilor este determinarea rezistentei lor la rupere .

Se apreciaza ca pentru determinarea rezistentei la rupere, cele mai corespunzatoare metode de calcul sunt cele bazate pe teoria starilor limita, teorie pe care se bazeaza metoda propusa de V.V.Sokolovski -K.V. Ruppeneit. Aceasta metoda a fost confirmata de Menzel si asimilata in calcule inca din 1973 de catre ICPM Cluj-Napoca si UNIVERSITATEA PETROSANI.

Conform acestei metodologii, tensiunile limita au valorile:

Pentru pilierii patrati - cazul Cocenesti:

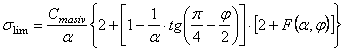[MPa]

Pentru pilierii(stalpii) dreptunghiulari:

[MPa]

In relatiile de mai sus, s-au folosit notatiile:

C_masiv - coeziunea aparenta a masivului, [MPa], si se determina din infasuratoarea cicloidala.

- valoarea unei functii dependente de coeficientul si unghiul de frecare interioara . Se stabileste cu ajutorul unei diagrame de tipul celei redate in fig. 5.6.

Valorile parametrului , rezultate din diagrama din fig.5.6, sunt valabile pentru si .

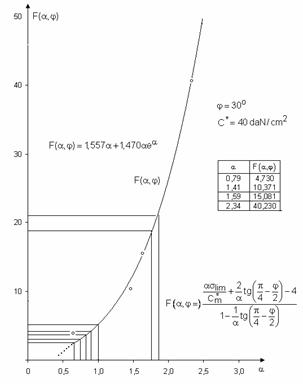
Fig.5.6. Metoda de calcul a functiei , dupa lucrarile lui Ruppeneit

Pentru valori ale lui si =, valorile acestui parametru pot fi luate din tabel 5.2.1 al lucrarii [6]. Pentru alte valori ale coeziunii C, respectiv ale unghiului de frecare interioara , parametrul se determina indirect, pornind de la conditia:

pentru a ne gasi in zona I-a de stabilitate.

- coeficient de sveltete a pilierilui, adica raportul dintre latimea pilierului si inaltimea acestuia, deci:

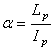
- unghiul de frecare interioara a rocii sau substantei minerale utile din pilier.

Tensiunea efectiva in pilier, se stabileste cu relatiile:

Pentru pilieri patrati:

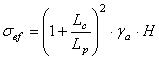[MPa]

Pentru pilierii lungi (dreptunghiulari)

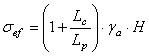[MPa]

unde:L_c si L_p reprezinta latimea camerei si respectiv, latimea pilierului;

H = H₁+ I_p- adancimea de la suprafata pana la baza pilierului (grosimea rocilor/sarii de deasupra pilierului - H₁ plus inaltimea lui - I_p), m;

- greutatea specifica aparenta a rocilor/ sarii de deasupra pilierului, N/.

Cunoscand valorile tensiunilor efective si a celor limita pot fi determinati gradul de solicitare si coeficientul de siguranta:

Functie de marimea celor doi parametri, durata de stabilitate a pilierului poate fi apreciata in conformitate cu tabel 5.2.

Tabel 5.2.Durata de stabilitate a pilierului

Pentru cazul Cocenesti-Valcea, luand in considerare caracteristicile sarii prevazute in tabelul 3.20 vom stabilii:

Diametrul cercului osculator al cicloidei:

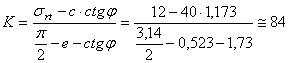daN/cm²

Infasurarea cicloidala pentru sarea de la Valcea este prezentata in fig. 5.7.

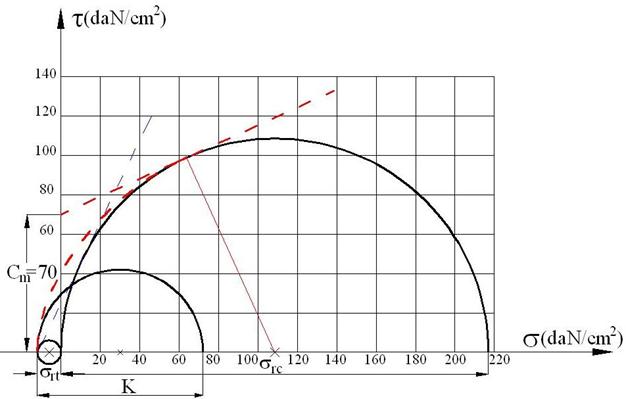
Fig. 5.7. Infasuratoarea cicloidala si determinarea valorii coeziunii aparente

pentru sarea de la Cocenesti-Valcea

Caracteristici:

daN/cm²

daN/cm²

c daN/cm²

C_m daN/cm²

K daN/cm²

Din fig.5.6 rezulta

Cu ajutorul acestor date, se calculeaza:

N/m³ → calculat la metoda Seniakov.

808 tf/m² = 80,8 daN/cm² = 8,08 MPa.

tf/m²

;

Rezulta ca, pilierii care se afla la primul orizont folosit in turism sunt stabili pentru o durata mai mare de 20 de ani - tebelul 5.2.

Pentru cazul celui de-al doilea orizont (in exploatare) din valoarea tensiunii efective se va scadea sarcina creata de primul orizont care a fost exploatat si care se stabileste cu relatia:

- numarul orizonturilor exploatate ();

- inaltimea camerei respectiv grosimea planseului;

- coeficient de extragere a sarii 0,5.

tf/m²

tf/m²

tf/m²

In acest caz: iar n = 7,36.

Concluziile raman neschimbate si pentru acest orizont.

Procedeul de calcul propus de M. Stamatiu

Acest procedeu de calcul face parte din grupa procedeelor care considera ca tensiunile asupra stalpilor (pilierilor) sunt repartizate neuniform.

Astfel, daca exista doua camere cu latimea d si stalpul dintre ele de latime d₁ si admitand ipoteza lui W.Ritter - V. Willman precum si ipotezele C.A. Coulomb - G. Rebhann, se poate considera ca asupra portiunii centrale de stalp de latime d₂ (fig.5.8) actioneaza o presiune , iar asupra partilor laterale va actiona o presiune data de greutatea rocilor din interiorul boltii de presiune.

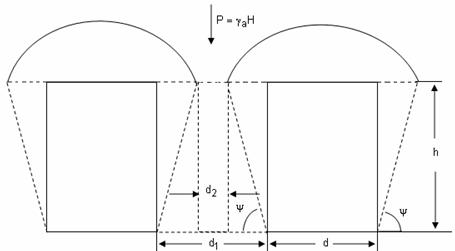
Fig.5.8. Calculul latimii stalpilor, dupa M.Stamatiu

Pornind de la relatia stabilita de M. Stamatiu pentru determinarea rezistentei esantioanelor de forma prismatica cu baza un patrat, se poate scrie:

- rezistenta de rupere la compresiune a esantionului prismatic cu baza un patrat;

- rezistenta de rupere la compresiune a esantionului sub forma de cub;

d - latimea epruvetei, respectiv a stalpului;

h - inaltimea epruvetei, respectiv a stalpului.

Inlocuind, rezulta:

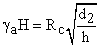
si de aici:

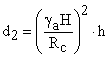
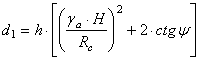
unde: si H - inaltimea de la nivelul stalpului pana la suprafata

Aplicand acest procedeu, rezulta:

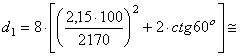9 m

Consideram ca acest procedeu da rezultate mult acoperitoare pentru conditia de stabilitate.

Diminuarea capacitatii portante a pilierilor datorata procesului de perforare-puscare

Daca pentru derocarea sarii se foloseste procesul de perforare-puscare, iar gaurile de mina sunt amplasate in apropierea suprafetelor laterale care delimiteaza pilierii respectiv planseul, atunci, efectul exploziei se transmite si in pilier-planseu, fisurandu-le pe o anumita adancime - micsorandu-le rezistenta prin diminuarea suprafetei portante - daca ne referim la pilieri. Daca, pilierul are o suprafata portanta: S = b² (pentru cazul pilierilor patrati), prin fisurare pe o adancime R, suprafata portanta se micsoreaza la: S` = (b - R)².

R - raza de fisurare;

b - latura pilierului.

Raza de fisurare depinde atat de natura rocii sau a substantei minerale utile in care se produce puscarea, cat si de caracteristicile explozivului folosit si se deduce cu relatia [11]:

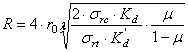[m]

r_o - raza gaurii de mina, [m];

rezistenta de rupere la compresiune a sarii, [N/m²];

rezistenta de rupere la tractiune a sarii, [N/m²];

coeficienti, care tin seama de modul de actionare a explozivului si au valorile:

coeficientul lui Poisson;

coeficientul de atenuare a undelor seismice:

y - caldura de explozie [J/kg];

- coeficient de transmitere a energiei:

- densitatea explozivului, [N/m³];

D - viteza de detonatie, [m/s];

- densitatea rocii, [N/m³];

Pentru usurinta calculelor, vom prezenta urmatoarele date [13], tabel numarul 5.3:

Tabel 5.3

Caracteristicile principale ale explozivilor [7].

Tabel 5.4

Caracteristicile sarii sunt cele prezentate in tabelul 3.20.

Daca, in calitate de exploziv folosim nitramon, atunci, determinam:

m

Cu alte cuvinte, pilierul - daca ne referim la pilieri - va fi afectat lateral pe o adancime de 0,64 m datorita fisuratiei, ca o consecinta a sistemului de perforare-puscare.

In consecinta, un pilier patrat cu latura de 15m si deci cu o suprafata portanta S = 225m², i-si va reduce suprafata portanta la:

m²

Cu alte cuvinte, suprafata portanta se reduce cu aproximativ 9%, ceea ce reduce si capacitatea portanta a pilierului aproximativ cu acelasi procentaj.

Daca in loc de nitramon vom folosii la puscare astralita, atunci:

m

Din acest calcul comparativ rezulta ca, pentru categorii diferite de explozivi, cu caracteristici destul de apropiate se obtin si adancimi de fisurare apropiate valoric.

Pentru diminuarea neajunsurilor create prin fisurarea pilierilor - scaderea capacitatii portante si diminuarea stabilitatii sistemului - camera, pilier, planseu, se recomanda:

redimensionarea pilierilor tinand seama de raza zonei de fisurare;

puscarea de netezire.

In urma acestei prezentari, este usor de apreciat cu cat contribuie fisuratia la scaderea stabilitatii complexului camera-pilier-planseu.

DIMENSIONAREA PLANSEELOR

Consideratii generale

Stabilitatea de ansamblu a excavatiilor create prin exploatarea sarii pe cale uscata prin metoda cu camere si pilieri abandonati nu depinde doar de comportarea pilierilor ci - mai ales in cazul structurilor de rezistenta multietajate - si de cea a planseelor.

Planseele pot fi:

a) plansee de tavan (intre linia de contact steril /sare si primul nivel de exploatare);

b) plansee de etaj (intre nivelele de exploatare).

Grosimea minima necesara de planseu care se afla in stare limita poate fi calculata pe baza parametrilor fizico - mecanici ai sarii geme din perimetrul in care au fost realizate camerele si pilierii, in functie de sarcinile ce actioneaza asupra planseului si de coeficientul de siguranta necesar.

Planseele trebuie sa preia greutatea rocilor situate deasupra deschiderii camerei de exploatare, fara a produce o deformare prea mare, insotita de aparitia de fisuri, crapaturi si desprinderea unor placi sau blocuri din sarea gema cuprinsa in limitele planseului de rezistenta.

Sarcinile care actioneaza asupra planseelor la exploatarea descendenta a etajelor prin metoda cu camere si pilieri patrati (sau dreptunghiulari) se estimeaza astfel

A. Sarcini fundamentale

greutatea proprie a planseului;

depasiri de greutate provocate de imprecizia executiei;

material depozitat pe planseu pe o banda de 4 - 5 m;

masini tehnologice in circulatie;

coeficienti dinamici.

Aceste sarcini se exprima prin relatia

MPa

in care :

h_n - grosimea nominala a planseului

si:

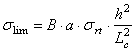MPa

B. Sarcini extraordinare, provocate in cazul saparii camerei de la etajul superior, traversand lucrari de deschidere terminate la pilierul urmator, care se exprima prin relatia :

Pentru camerele cu tavan plan grosimea nominala a planseului reprezinta grosimea reala a acestuia.

In cazul in care camerele se fac cu bolta, grosimea nominala a planseului rezulta din relatia:

unde:

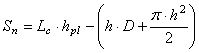- sectiunea transversala nominala a planseului;

L_c - latimea camerei;

h_pl - grosimea planseului;

- raza de boltire a tavanului camerelor de exploatare (dupa M.M.Protodiakonov);

a - semideschiderea camerelor;

f - coeficient de tarie a sarii.

D - diametrul cercului de boltire = 2h.

Daca: L_c = 16 m; h_pl = 8 m; ; ; f = 2; a = 8m; D = 8

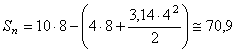m²

m

Principiile de baza aplicate in dimensionarea planseelor

In general, sunt cunoscute doua principii de calcul si anume:

principiul clasic al rezistentelor admisibile;

principiul coeficientilor de siguranta.

Principiul rezistentelor admisibile se aplica de regula in sectorul constructiilor de masini si el se bazeaza pe introducerea in calcul a unor rezistente specifice a materialelor, micsorate mult, atat fata de limita de rupere cat si fata de limita de elasticitate,. Aceasta rezistenta micsorata este denumita rezistenta admisibila si introducerea in calcul a acestei valori are scopul de a mentine materialul, pe parcursul exploatarii, in limitele unui comportament strict elastic.

Principiul coeficientilor de siguranta este aplicat in special, in sectorul constructiilor, la materialele care nu respecta legea lui Hooke si la care in consecinta, oricat s-ar micsora rezistenta specifica introdusa in calcul tot nu ar exista garantia unui comportament elastic.

Rocile si substantele minerale utile se inscriu in randul materialelor care au , domeniul lor de comportament elastic este fie extrem de redus, fie total inexistent. In consecinta, dimensionarea in minerit se considera a fi corecta numai daca se pleaca de la principiul coeficientilor de siguranta, care se bazeaza pe determinarea sarcinii limita ce produce distrugerea structurii de rezistenta si apoi (prin impartirea acesteia cu un coeficient de siguranta adoptat- n) a incarcarii efectiv admise.

Relatia de baza este urmatoarea:

Determinarea portantei la rupere a unui planseu asimilat cu o grinda

Considerandu-se planseul ca o grinda dublu incastrata si incarcata cu o sarcina uniform distribuita p, momentul incovoietor este maxim in punctele de incastrare si are urmatoarea valoare:

in care: este deschiderea grinzii, respectiv deschiderea camerei de exploatare.

Conform relatiei lui Navier, momentul capabil (la rupere) al unei grinzi cu sectiunea dreptunghiulara, avand latimea egala cu unitatea (b=l), se poate scrie sub forma :

in care: este rezistenta la rupere a grinzii si h - grosimea grinzii.

Punand conditiile la limita si egaland cele doua momente, se obtine portanta la rupere:

Relatia de mai sus este utilizata pentru determinarea portantei la rupere a planseelor. Conform relatiilor anterioare, incarcarea efectiva admisa a planseului devine:

unde n este coeficientul de siguranta.

Punand conditia de nefisurare a planseului in relatia de mai sus, in loc de la compresiune se foloseste valoarea rezistentei de rupere la tractiune si in consecinta relatiile devin:

La materialele care nu respecta legea lui Hooke, calculul portantei dupa aceasta relatie ascunde o sursa de supradimensionare. Aceasta rezerva ascunsa este cauzata de faptul ca la materialele respective (cum este sarea gema), desi deformatiile raman proportionale cu distanta fata de axa neutra (legea lui Bernoulli), totusi relatia lui Navier nu este respectata; ea ramane valabila si constituie baza calculului de incovoiere numai strict in domeniu de comportare elastica si numai daca .

Dar, la sarea gema:

Dupa prof. Stamatiu,

Eforturile reale de tractiune ce se nasc intr-o anumita sectiune sunt mai mici decat cele determinate dupa relatia lui Navier.

Pentru sarea gema, momentul capabil (momentul incovoietor maxim in planseu) al unei grinzi poate fi scris corect sub forma:

unde: a - coeficient de corectie determinat experimental, [33];

Pentru sare a = 1,3; pentru andezite a = 1,76; pentru calcare a = 1,57; pentru betoane a = 1,7.

Tinand cont de relatiile mentionate mai inainte, relatia generala de calcul a grosimii planseelor se deduce din:

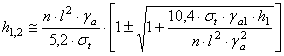[m]

In cazul in care coperta de roci sterile are o grosime neglijabila, relatia are forma mult mai simplificata:

si - greutatea specifica aparenta si grosimea rocilor acoperitoare;

- greutatea specifica aparenta a sarii din planseu.

Dimensionarea planseelor de pe premisele placilor incastrate

La placi, solicitarea principala este incovoierea. Aceasta solicitare da nastere la tensiuni atat in planul de sus al placii cat si in planul de jos. Tensiunile , perpendiculare pe planul placii sunt egale cu incarcarea exterioara . Pe partea incarcata , iar pe cea libera

Tensiunile dau nastere, in ambele planuri ale placii la tensiuni ce se evidentiaza atat pe directia x cat si pe directia y, rezultand conform axelor respective de coordonate, tensiunile orizontale si .

Valoarea tensiunilor orizontale depinde de incarcarea p, de grosimea planseului h, de forma si deschiderea sa I.

La verificarea conditiei de stabilitate a planseelor se pune conditia :

in care:

si sunt rezistentele de rupere la tractiune si respectiv la compresiune a rocii ce constituie planseul;

n - coeficient de siguranta.

si - tensiunile maxime reale de tractiune, respectiv de compresiune, care iau nastere in planseul supus la verificare, determinate dupa relatiile din tabel 5.5 functie de forma planseului, de incarcarea sa efectiva, de deschiderea L, de grosimea sa h si de coeficientul de corectie a corespunzator rocii constitutive a planseului.

Functie de forma planseului, se ia in considerare relatia tensiunilor maxime de tractiune, conform tabel 5.5. De exemplu, in cazul unei placi plane de forma patrata, avem:

pentru placa dreptunghiulara cu raportul laturilor L/l = 1,5:

Tabel 5.5. Relatiile pentru calculul tensiunilor reale din placile incastrate constituite din roci

Tabel 5.5. (continuare)

pentru placa circulara :

- pentru placa eliptica L/l = 1,5:

Relatia de baza in dimensionarea planseelor constituite din roci se supune principiului starii limita (sau a capacitatii portante) si anume:

sau

unde: - portanta planseului la limita;

n - coeficientul de siguranta.

Pentru ca din relatia de mai sus sa rezulte grosimea necesara de planseu, trebuie ca si p sa fie explicitati prin h.

Stiind ca:

in care:

- greutatea proprie a planseului,

q_s - greutatea suplimentara (ce intervine in cazul planseelor de tavan) exercitata pe planseu de catre rocile acoperitoare.

Deci:

Inlocuind rezulta:

in care: B - coeficient care tine seama de forma placii, iar valorile lui sunt prezentate in tabelul 5.6.

Tabel 5.6.Valorile coeficientului (B)

Din relatia anterioara se ajunge la o ecuatie de gradul doi, de forma:

(2.59)

Rezolvarea acestei ecuatii ne conduce la radacinile:

In cazul in care exista incarcare suplimentara:

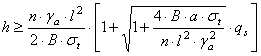, m

In cazul in care nu exista incarcare suplimentara:

, m

Incarcarea suplimentara se calculeaza cu relatia:

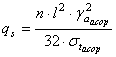
in care:

- greutatea specifica aparenta medie a rocilor acoperitoare, [N/m³];

- rezistenta de rupere la tractiune ca valoare medie a rocilor acoperitoare, [MPa];

n - coeficient de siguranta.

Valorile stabilite prin calcul se compara cu valorile reale din teren, iar functie de coeficientii de siguranta din tabelul 5.7 se determina durata de stabilitate.

Tabel 5.7. Durata de stabilitate a planseelor, functie de coeficientul de siguranta

Un procedeu de calcul mult mai simplu si acoperitor din punct de vedere al rezultatelor, porneste de la ecuatiile lui Bernoulli si Navier pentru grinzile drepte cu sectiune constanta supuse la incovoiere.

Pentru aceste grinzi:

- rezistenta de rupere la incovoiere a rocii sau a substantei minerale utile din grinda;

W - modulul de rezistenta.

Pentru un planseu cu lungimea unitara:

iar

Inlocuind rezulta:

m

L_c - latimea camerei.

Verificarea grosimii planseelor pentru Cocenesti-Valcea

Asa cum am aratat in acest paragraf, vom face distinctie intre planseul de tavan si planseul de etaj.

In cazul planseului de tavan

Incarcarea suplimentara creata de greutatea rocilor acoperitoare - care au grosimea de 50 m, greutatea specifica aparenta N/m³ si o rezistenta la tractiune de 5 daN/cm² - poate fi calculata cu relatia: (pentru n = 4)

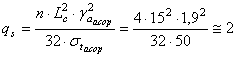tf/m²

Pornind de la premiza placilor incastrate si considerind caracteristicile sarii din tabelul 3.20 pentru a = 1,3; n = 4 si B = 3,22 rezulta:

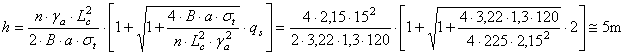
Dupa cum, planseul de tavan are grosimea de aproximativ 50 m, rezulta ca stabilitatea acestuia este asigurata.

In ce priveste planseul de etaj

In cazul planseelor de etaj, incarcarea suplimentara este creata de greutatea sarii care rezulta la o impuscare si care se repartizeaza pe o banda de 4 - 8 m de planseu si pe toata latimea camere, cat si de greutatea utilajelor care se gasesc simultan pe planseu.

Daca: L_c = 15 m, I_c = 8 m; saltul la o puscare este de 1,9 m, iar N/m³, rezulta ca, la o puscare se disloca o cantitate de sare de:

tf

Suprafata pe care se repartizeaza aceasta sare in urma puscarii va fi:

m²

De aici:

tf/m²

Daca in front se vor afla simultan, doua autobasculante de (16 + 10) t fiecare, vom avea:

tf

tf/m²

Incarcarea suplimentara totala va fi:

tf/m²

In acest caz, grosimea de planseu va fi:

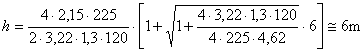
Dupa cum planseul de etaj are grosimea de 8 m, rezulta ca acesta va fi stabil.

Din tabelul 5.7, rezulta ca durata de stabilitate a planseului este mai mare de 70 de ani.

Coeficientul de siguranta corespunzator planseului cu grosimea de 8 m rezulta din:

unde:

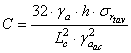si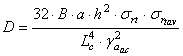

Explicitand rezulta:

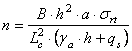
Inlocuind rezulta:

CONCLUZII

Dupa cum rezulta din acest capitol, aplicand metode clasice am realizat un calcul de stabilitate a sistemului camera-pilier-planseu.

In ce priveste camerele de forme dreptunghiulare, calculele ne arata ca stabilitatea acestora este asigurata pentru coeficienti de siguranta n14, atat pentru deschiderea camerelor cat si inaltimea acestora.

In cazul pilierilor, coeficientul de siguranta oscileaza in jurul valorii n8, prezentand o durata de stabilitate mai mare de 20 de ani (in cazul pilierilor fara fisuri) si de n6 (pentru pilierul fisurat). Exceptia de la aceste concluzii este data de procedeul de calcul al lui SEVIAKOV, care a lansat procedeul luand in considerare rezistenta de rupere a sarii obtinuta pe cuburi, iar noi am lucrat cu rezistenta obtinuta pe cilindrii.

Planseele sunt stabile prezentand coeficienti de siguranta mai mari de n ≥ 3, cu durata de stabilitate mai mare de 60 de ani.

Tinand seama de aceste concluzii, si de faptul ca orizontul 260 este trecut in circuitul turistic, este necesar sa se imbunatateasca conditiile de stabilitate ale pilierilor respectiv ale planseelor folosindu-se in procesul de derocare asa numita puscare de netezire - care reduce numarul si profunzimea fisurilor -.