| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
Lesson Title: Fourier Transform
Lesson Number: 26
|
|
![]()
Background:
In Chapter 11 the basic form of the Fourier transform and series was established. The Fourier transform pair was defined as:
![]()
The Fourier transform was said to exist if the signal is absolutely integrable (although this is not a necessary condition). At times, the production of a Fourier transform of series can be a straightforward calculation (e.g., pulse), at other times it requires great finesse. The difficult cases can often be resolved by properly interpreting the inverse transform equation as illustrated below. Fortunately many of the important transforms are summarized in Tables 11.2 with properties given in Table 11.3.
Challenge:
1. What is the inverse Fourier transform of d(w-w0)?
 2. Suppose
x(t)=sgn(t)= (see Figure 1), what is X(jw)?
2. Suppose
x(t)=sgn(t)= (see Figure 1), what is X(jw)?
Figure 1: sgn function.
Response:
1. Inverse Fourier transform if a line spectrum d(w-w0).
![]()
Therefore, fince ![]() ,
, ![]() . Notice computing the Fourier transform of
. Notice computing the Fourier transform of ![]() directly is far more
challenging as suggested below.
directly is far more
challenging as suggested below.
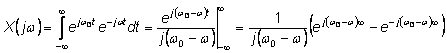
You need to evaluate this integral as w w0 from both sides. Your on your own from this point on.
2. Suppose x(t)=sgn(t).
Notice that x(t) is technically not absolutely integrable. Nevertheless, its Fourier transform exists and can be computed as shown below. Approximate the sgn function using the decaying exponentials shown in Figure 1. That is:
![]()
Then
![]()
which has a magnitude of 2/w, which peaks at w=0, and a phase shift equal to -90 for w³0 and 90 for w<0.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1253
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved