| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
Polarization of light
The existence of polarization phenomena is a direct
consequence of light being a transverse
wave. The electric field vector
of an electromagnetic wave can always be resolved into two components parallel
to the coordinate axes in the plane of its oscillation. Let ![]() label the direction of travel of the light
and
label the direction of travel of the light
and ![]() and
and ![]() be directions in the plane of the electric
field. Then the components of the electric field vector of the light wave will
oscillate as
be directions in the plane of the electric
field. Then the components of the electric field vector of the light wave will
oscillate as
![]() , ( . )
, ( . )
![]() , ( . )
, ( . )
where a difference in phase ![]() between the two disturbances was introduced.
According to the ratio of magnitudes
between the two disturbances was introduced.
According to the ratio of magnitudes ![]() and phase relationship which is determined by
and phase relationship which is determined by ![]() ,
the wave can be linearly, circularly or elliptically polarized.
,
the wave can be linearly, circularly or elliptically polarized.

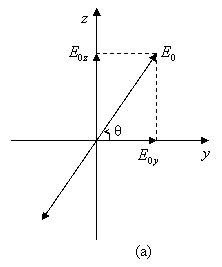
With linear
polarization, the direction of the electric field vector resides in a fixed plane and it
stays constant at any point in space, at any time. Since the plane of
oscillation has a fixed position, this type of polarization is also called plane
polarization. The electric field makes a constant angle ![]() to the
to the ![]() direction, as in the illustration.
direction, as in the illustration.
The electric field vector oscillates in space and in
time at the frequency of the light wave. If the direction of ![]() is constant in space, then the variations
of
is constant in space, then the variations
of ![]() must be in-step along
must be in-step along ![]() and
and ![]() directions. Thus, for
directions. Thus, for
![]() ( . )
( . )
the electric field vector oscillates as
![]() ( . )
( . )
in the direction described by the angle
![]() ( . )
( . )
See the figure (a) above.
The amplitude of the oscillation is given by
![]() . ( . )
. ( . )
Similarly, for
![]() ( . )
( . )
the component disturbances are out of phase and the electric field vector of the linearly polarized wave oscillates as
![]() ( . )
( . )
in a direction which makes an angle
![]() with the Oy
axis. See the figure (b) above.
with the Oy
axis. See the figure (b) above.
Note that an arbitrary linear state of polarization, which is sometimes
designated as a P -state (from
plane state of polarization), can always be expressed in terms of two
orthogonal linearly polarized states, which have a difference in phase ![]() given by (1.3) or (1.7).
given by (1.3) or (1.7).
With circular
polarization, the direction of the electric field vector is no longer fixed. In fact, it
rotates in time, so that the tip of ![]() sweeps out a circular helix whose axis
coincides to the direction of propagation of the wave. The frequency of
rotation is the wave frequency. In circularly polarized light two different
states of polarization are possible: right and left. If an observer looking
toward the source (the wave is approaching him) can detect a clockwise rotation
of
sweeps out a circular helix whose axis
coincides to the direction of propagation of the wave. The frequency of
rotation is the wave frequency. In circularly polarized light two different
states of polarization are possible: right and left. If an observer looking
toward the source (the wave is approaching him) can detect a clockwise rotation
of ![]() ,
the wave is right circularly polarized
R
-state. If the rotation
is counterclockwise, the wave is left circularly polarized L-state
,
the wave is right circularly polarized
R
-state. If the rotation
is counterclockwise, the wave is left circularly polarized L-state
An arbitrary right circular state of
polarization can be expressed in terms of two orthogonal P-states of equal amplitude ![]() ,
whose difference in phase is given by
,
whose difference in phase is given by
![]() . ( . )
. ( . )
Thus the component disturbances are
![]() ( . )
( . )
and
![]() . ( . )
. ( . )
Notice that when ![]() reaches its maximum value,
reaches its maximum value, ![]() is null and vice versa, so that the tip of the
light vector in the R-state of polarization
is null and vice versa, so that the tip of the
light vector in the R-state of polarization
![]() ( . )
( . )
rotates
clockwise on a circle of radius ![]() while traveling in the
while traveling in the ![]() direction as well.
direction as well.
The L-state of polarization is a superposition of two orthogonal P-states of equal amplitudes and a difference in phase
![]() . ( . )
. ( . )
Thus
![]() ( . )
( . )
and
![]() . ( . )
. ( . )
The resultant L-state wave field is a superposition of (1.14) and (1.15)
![]() , ( . )
, ( . )
i.e. a
vector of constant amplitude ![]() which rotates counterclockwise at the wave
frequency
which rotates counterclockwise at the wave
frequency ![]() .
.
It is interesting that by overlying an R-state wave field and an L-state wave field, a P-state wave field of the same frequency is obtained. Indeed we have
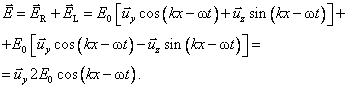 ( . )
( . )
This result can be written as
![]() . ( . )
. ( . )
It states that any P-state wave field can be described as a superposition of an R- and L-state, provided that their amplitudes are equal.
The linear and circular states of polarization are particular cases of the elliptical polarization of light. In a wave which is elliptically polarized the electric field vector rotates at the wave frequency thus changing its direction and amplitude (as opposed to the circular polarization, where the amplitudes remains constant). Its tip sweeps out an elliptical helix. This state is designated as the E-state of polarization and it can be described as a superposition of two P-states of the form (1.1) and (1.2), where the difference in phase does not coincide with the values given by (1.3) (1.7) (1.9) or (1.13)
To prove that the amplitude varies elliptically we eliminate the time variable between the equations describing the component disturbances. We have
![]() ( . )
( . )
and
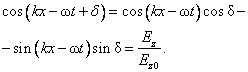 ( . )
( . )
Using the fundamental trigonometric identity and (1.19), we obtain
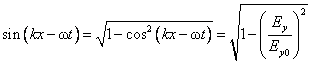 . ( . )
. ( . )
Next we take equations (1.21) and (1.19) into the second equality of equation (1.20). It results:
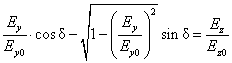 ( . )
( . )
By isolating the square root and consequently squaring the obtained equation, we get
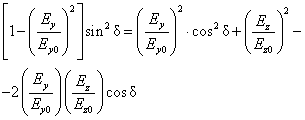 ( . )
( . )
which yields
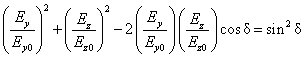 . ( . )
. ( . )
This is the equation of an
ellipse which is tilted with respect to the ![]() axis at an angle
axis at an angle ![]() given by
given by
![]() . ( . )
. ( . )
Recall
that any state of polarization can be described as a superposition of two
linear polarizations in perpendicular directions. When we discussed the reflection
and refraction of light, we considered the directions of propagation without regard
of the amount of incident light which is reflected and transmitted,
respectively. The corresponding fractions depend on the state of polarization
of the incident light. The coefficients of reflection and transmission at the
boundary surface between two different media are computed in Maxwells
classical theory of electromagnetism. They are given by the Fresnel
relations. Two types of coefficients are defined. The amplitude
coefficients of reflection parallel and
perpendicular to the plane of incidence are denoted by ![]() and
and ![]() . They are expressed as
. They are expressed as
![]()
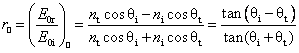 ( )
( )
and
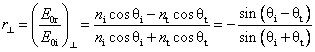 , ( )
, ( )
where ![]() and
and ![]() are the angle of incidence and the angle of
refraction (recall that the angle of reflection is equal to the angle of
incidence according to the law of reflection). In the previous equations
are the angle of incidence and the angle of
refraction (recall that the angle of reflection is equal to the angle of
incidence according to the law of reflection). In the previous equations ![]() and
and ![]() denote
the disturbance amplitudes in the incident wave and in the reflected wave. The
corresponding state of polarization was designated by using the indices
denote
the disturbance amplitudes in the incident wave and in the reflected wave. The
corresponding state of polarization was designated by using the indices ![]() and
and ![]() for the parallel and perpendicular directions
of polarization with respect to the plane of incidence. In the last equality of (26) and (27), respectively
Snells law was used to eliminate the refractive indices.
for the parallel and perpendicular directions
of polarization with respect to the plane of incidence. In the last equality of (26) and (27), respectively
Snells law was used to eliminate the refractive indices.
The intensity coefficients of reflection in the parallel and perpendicular directions are defined as irradiance ratios. They are also named reflectance coefficients or simply reflectance. The corresponding Fresnel equations are
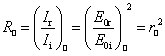 ( )
( )
and
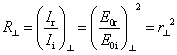 ( )
( )
At
normal incidence ![]() ,
we obtain
,
we obtain
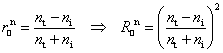
and
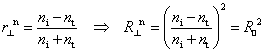 ,
,
which means that the reflectance of light whose
polarization is parallel to the plane of incidence is equal to the reflectance
of light with normal polarization. For air-glass interface ![]() ,
the reflectance coefficients are given by
,
the reflectance coefficients are given by
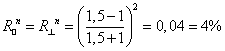 ( )
( )
Only 4% of the incident light is thus reflected and the rest is transmitted.
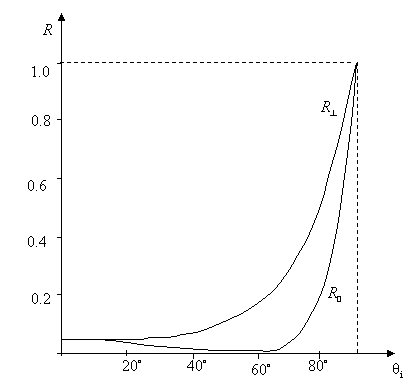
In
the figure above, the dependence of the reflectance on the incidence angle is
presented. The intensity reflectance ![]() of the perpendicular state of polarization increases
monotonously from 4%- the value corresponding to the normal incidence
of the perpendicular state of polarization increases
monotonously from 4%- the value corresponding to the normal incidence ![]() -
to 100% at grazing incidence, that is
-
to 100% at grazing incidence, that is ![]() .
.
![]() has a more complex
behavior: for small angles it decreases from 4% to zero, then increases to 100%
as
has a more complex
behavior: for small angles it decreases from 4% to zero, then increases to 100%
as ![]() does. Equations (26) and (28) yield that the
zero reflectance of the parallel polarization occurs at a particular angle of incidence
does. Equations (26) and (28) yield that the
zero reflectance of the parallel polarization occurs at a particular angle of incidence ![]() ,
where
,
where
![]() ( )
( )
(![]() is called the Brewster angle of incidence after the
name of the scientist who discovered this phenomenon). As a result, light
reflected at this angle will be totally polarized in a direction which is
perpendicular to the plane of incidence since
is called the Brewster angle of incidence after the
name of the scientist who discovered this phenomenon). As a result, light
reflected at this angle will be totally polarized in a direction which is
perpendicular to the plane of incidence since![]() (see the figure above). As far as the transmitted light is concerned, it is
partially polarized, predominantly in the parallel direction, as the figure
below indicates.
(see the figure above). As far as the transmitted light is concerned, it is
partially polarized, predominantly in the parallel direction, as the figure
below indicates.
Let
us calculate the angle ![]() as a function of the refractive indices of the
two media. According to Snells law
as a function of the refractive indices of the
two media. According to Snells law
![]() ,
,
where
equation (31) was used to eliminate the angle of refraction ![]() .
Then
.
Then
![]() ( )
( )

For air-glass interface
![]()
Applications
1. Brestwers angle polarizer is composed of a stack of plates disposed so that the natural light is incident at Brewsters angle. The reflected light will be polarized in a direction perpendicular to the incidence plane (horizontal) and the transmitted light will be polarized in a direction parallel to the incidence plane (vertical).
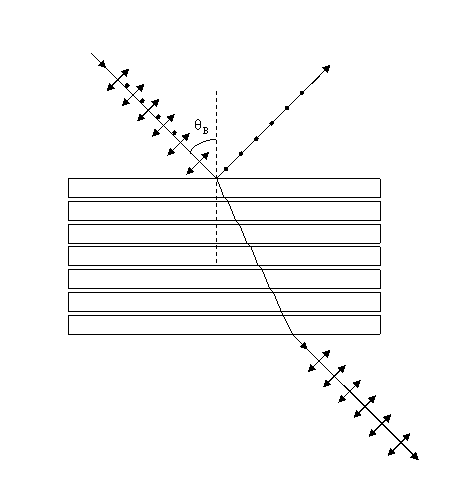

2. Bresters window
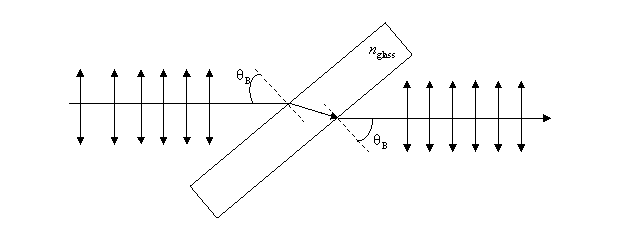 A device which transmits 100%
polarized light, without losses by reflection. It is used in laser systems as
exit window for polarized laser light.
A device which transmits 100%
polarized light, without losses by reflection. It is used in laser systems as
exit window for polarized laser light.
As we could see, the propagation of light in a transparent medium and at interfaces depends on the optical properties of the medium and on the polarization of light. The optical properties are described by the refractive index. If a certain material has a refractive index which is the same in any direction for a monochromatic wave, then the material is said to be optically isotropic. The velocity of the wave is obviously, the same in any direction. Most of the gasses, liquids, unstressed amorphous solids and certain highly symmetrical crystalline substances are optically isotropic. Many crystals are however optically anisotropic. The optical properties of an anisotropic crystal depend on the direction of propagation of electromagnetic waves. In other words, the refractive index and the wave velocity depend on the direction in which light travels through the crystal. An uniaxial anisotropic crystal has a single symmetry axis which is called the optic axis and two principal indices of refraction. The optic axis is actually a direction in the crystal characterized by a single index of refraction.
Calcite(![]() ,
,
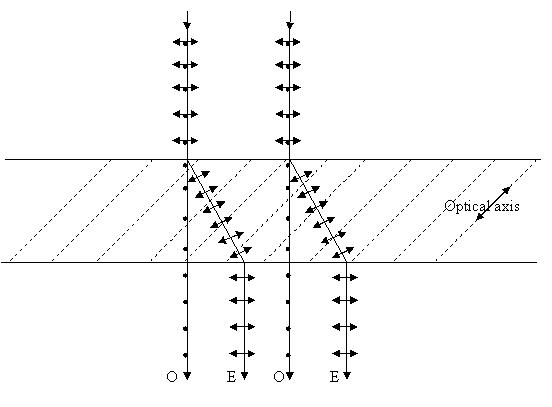
 Each
ray in the incident beam is split into two rays which propagate differently in
the crystal. One ray, named the ordinary ray, obeys Snells law of
refraction while the other, named the extraordinary ray does not. The two
rays propagate in the crystal at different velocities (in the direction of the
optic axis the velocities of the two rays are equal). This property of some crystals
is called birefringence, meaning double refraction. A birefringent
crystal which has only one optic axis is called uniaxial. There also exist
biaxial crystals.
Each
ray in the incident beam is split into two rays which propagate differently in
the crystal. One ray, named the ordinary ray, obeys Snells law of
refraction while the other, named the extraordinary ray does not. The two
rays propagate in the crystal at different velocities (in the direction of the
optic axis the velocities of the two rays are equal). This property of some crystals
is called birefringence, meaning double refraction. A birefringent
crystal which has only one optic axis is called uniaxial. There also exist
biaxial crystals.
As a result of its birefringence, a calcite crystal will produce two different images of an object which is placed under it. One of the images is right above the object and the other is laterally shifted. A polarizer placed on top of the crystal can be oriented so that only one of the images is transmitted through it. If one rotates the crystal one of the images will rotate as well.
Such a peculiar behavior was explained by Huygens, although the polarization phenomenon was not known at that time. Let us consider a point source of monochromatic light imbedded in a uniaxial crystal, as calcite. The source produces two wave fronts: the ordinary wave front is spherical and the extraordinary wave front, which is ellipsoidal.
As we said, it
is customary to describe the optical properties in terms of the refractive
index. The uniaxial birefringent has two indices of refraction: the ordinary
refractive index, denoted by ![]() ,
and the extraordinary refractive index, denoted by
,
and the extraordinary refractive index, denoted by ![]() .
.
![]() has a single value
while
has a single value
while ![]() has values in the range
has values in the range ![]() .
The minimum value of
.
The minimum value of ![]() is given in tables since it is the principal
extraordinary refractive index. For simplicity, we denote the principal value
of the refractive index by
is given in tables since it is the principal
extraordinary refractive index. For simplicity, we denote the principal value
of the refractive index by ![]() instead of
instead of ![]() .
For calcite, we have
.
For calcite, we have
![]() .
.
The difference between the two principal refractive indices is given by
![]()
If ![]() then
then ![]() and the crystal is negative uniaxial. If
and the crystal is negative uniaxial. If ![]() then
then ![]() and
the crystal is positive uniaxial. In
table 1 some uniaxial crystals are presented.
and
the crystal is positive uniaxial. In
table 1 some uniaxial crystals are presented.
|
|
|
|
|
|
Ice |
1,309 |
1,313 |
0,004 |
|
Quartz |
1,544 |
1,553 |
0,009 |
|
Calcite |
1,658 |
1,486 |
-0,172 |
|
Tourmaline |
1,669 |
1,638 |
-0,032 |
|
Sapphire |
1,768 |
1,759 |
-0,008 |
Table 1
As we have already mentioned, in birefringent uniaxial crystals there is a unique direction in which the ordinary wave O and extraordinary wave E propagate at the same velocity and that is called optic axis. Consider a point source which is embedded in a uniaxial crystal. The ordinary wave front is spherical while the extraordinary wave front is ellipsoidal. There are two cases:
1. Negative uniaxial crystals
![]() In
such birefringent media E propagates faster than O. The figure shows the two
corresponding wave fronts. By
In
such birefringent media E propagates faster than O. The figure shows the two
corresponding wave fronts. By ![]() the direction polarization of O is indicated
(it is
the direction polarization of O is indicated
(it is
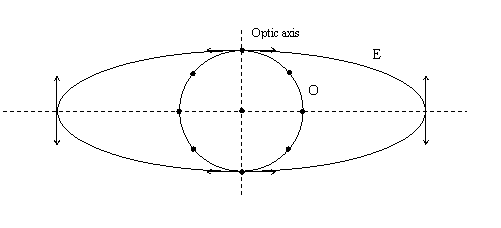
perpendicular to the plane of incidence). By ![]() the direction of polarization of E is
indicated (it is parallel to the plane of incidence).
the direction of polarization of E is
indicated (it is parallel to the plane of incidence).
According to the
figure the velocity of O is the same in any direction. We designate it by ![]() .
The implication is that the refractive index seen by O is also the same in any
direction. We denote it by
.
The implication is that the refractive index seen by O is also the same in any
direction. We denote it by ![]() .
.
The velocity of
E, ![]() (which stands for
(which stands for ![]() )
changes with the direction of propagation. Its maximum value
)
changes with the direction of propagation. Its maximum value ![]() is reached when E propagates normally to the
optic axis. The minimum value
is reached when E propagates normally to the
optic axis. The minimum value ![]() corresponds to the propagation along the optic
axis. Thus
corresponds to the propagation along the optic
axis. Thus ![]() .
.
The refractive
index seen by E ![]() ,
is no longer constant. In fact, it is maximum in the direction where
,
is no longer constant. In fact, it is maximum in the direction where ![]() is minimum, that is along the optic axis,
where the refractive index is
is minimum, that is along the optic axis,
where the refractive index is ![]() .
The minimum refractive index corresponds to the maximum velocity of E, i.e. in
a direction perpendicular to the optic axis. We denote it by
.
The minimum refractive index corresponds to the maximum velocity of E, i.e. in
a direction perpendicular to the optic axis. We denote it by ![]() .
Thus
.
Thus ![]() .
The two limit values of the refractive index seen by E are named principal
refractive indices and they can be found in tables (see table 1).
Examples of negative uniaxial crystals are: calcite, sapphire, tourmaline.
.
The two limit values of the refractive index seen by E are named principal
refractive indices and they can be found in tables (see table 1).
Examples of negative uniaxial crystals are: calcite, sapphire, tourmaline.
2. Positive uniaxial crystals
Positive uniaxial crystals are birefringent media in which the extraordinary wave propagates slower than the ordinary wave (see the figure below).
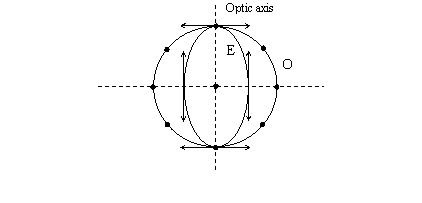
The velocity of the extraordinary wave is thus smaller than that of the
ordinary wave ![]() .
This is due to the fact that the principal extraordinary refractive index is
larger that the ordinary refractive index
.
This is due to the fact that the principal extraordinary refractive index is
larger that the ordinary refractive index ![]() .
Again the ordinary wave sees the same refractive index in any direction. For
positive uniaxial the relation for the refractive index is
.
Again the ordinary wave sees the same refractive index in any direction. For
positive uniaxial the relation for the refractive index is ![]() ,
meaning that the principal value along the optic axis is minimum while the
principal value in the direction perpendicular to the optic axis is maximum, as
opposed to the negative uniaxial crystals. Examples of positive uniaxial
crystals are quartz and ice. As we have already mentioned, biaxial birefringent
crystals also exist: mica, turquoise, topaz a. o. They have two symmetry axes,
but they are beyond the goal of this course.
,
meaning that the principal value along the optic axis is minimum while the
principal value in the direction perpendicular to the optic axis is maximum, as
opposed to the negative uniaxial crystals. Examples of positive uniaxial
crystals are quartz and ice. As we have already mentioned, biaxial birefringent
crystals also exist: mica, turquoise, topaz a. o. They have two symmetry axes,
but they are beyond the goal of this course.
The properties of birefringent uniaxial crystals are used in several optical devices to produce the splitting of the incident beam followed by its polarization (the Wollaston polarizing beam splitter, the Nicol prism) and the rotation of incident linearly polarized light (the half wave plate). They are also used to obtain circularly polarized light (the quarter wave plate) or ellipsoidal polarized light (arbitrary wave plates).
It is obvious that the propagation of light in birefringent crystals depends on the direction of polarization and on the direction of propagation with respect to the optic axis. We shall first consider the not so interesting case where natural light is incident on a plate made of a negative uniaxial crystal in the direction of the optic axis.
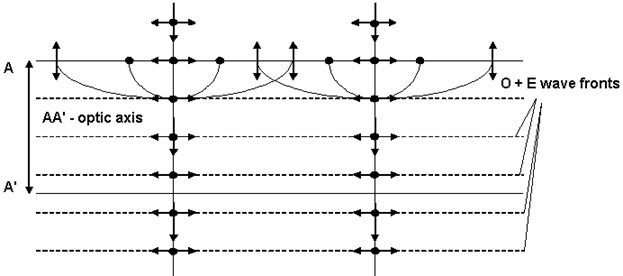
As you can see, the ordinary and the extraordinary wave fronts are traveling together in the plate as a single wave. The separation of the different states of polarization does not occur and the propagation in the direction parallel to the optic axis is similar to the propagation in an isotropic material.
The situation in completely changed if the optic axis is lying in a plane perpendicular to the direction of propagation (see the figure).
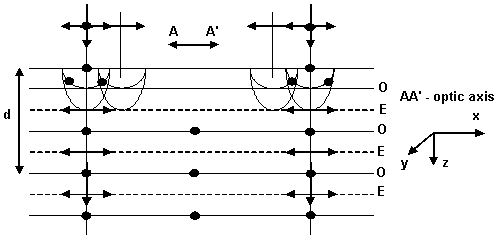
Again the
direction of propagation of O and E are the same. However they propagate at different
velocities ![]() and
and ![]() ,
respectively. As a result, although initially the two are in-phase, O will be
delayed with respect to E (in a negative uniaxial crystal plate, as calcite).
If the crystal is positive uniaxial then E will lag behind O.
,
respectively. As a result, although initially the two are in-phase, O will be
delayed with respect to E (in a negative uniaxial crystal plate, as calcite).
If the crystal is positive uniaxial then E will lag behind O.
Such plates are called retarders. They introduce a difference in-phase between the ordinary and extraordinary waves and thus, a phase shift. After crossing the plate, the superimposed ordinary and extraordinary waves that are shifted in phase will form a single wave whose state of polarization is different from the initial one. In the following we will consider some particular plates made of calcite.
Half wave plates
Consider a reference
system ![]() as in the figure. The direction of the optic
axis is
as in the figure. The direction of the optic
axis is ![]() and the incident linearly polarized light is
propagating in the
and the incident linearly polarized light is
propagating in the ![]() direction. The vibrations of the electric
field vector at z (the incidence plane) are presented in the figure.
direction. The vibrations of the electric
field vector at z (the incidence plane) are presented in the figure.
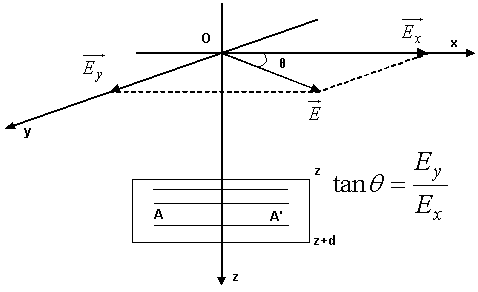
They are given by:
![]() ( )
( )
and
![]() ( )
( )
The electric field vector ![]() makes an angle θ with the optic axis
makes an angle θ with the optic axis
![]() ( )
( )
After traversing the plate of thickness d, at z+d the extraordinary wave will lead in phase the ordinary wave by an angle of π
![]() , ( )
, ( )
where λ0 is the wavelength of the incident monochromatic wave in vacuum. This corresponds to a difference in optical path length of half a wave (λ/2) and this is where the plate gets its name from. As a result:
![]() ( )
( )
and
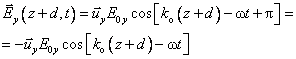 ( )
( )
As you can see in the figure
below, ![]() makes in the end an angle θ with the
optic axis. So, the result of incident light traversing the half wave plate is
a rotation of the direction of polarization by an angle 2θ.
makes in the end an angle θ with the
optic axis. So, the result of incident light traversing the half wave plate is
a rotation of the direction of polarization by an angle 2θ.

Notice that the condition for a half-wave plate to work with some specific monochromatic
incident light involves the wavelength. Indeed we have:
![]() ( )
( )
This means that half-wave plates are designed specifically for particular wavelengths.
Let us find the
minimum thickness d of a half wave plate of calcite which is used with
light at ![]() in air. The number of waves which span d
in the extraordinary wave is
in air. The number of waves which span d
in the extraordinary wave is
![]() ( )
( )
and,
correspondingly, the number ![]() is
is
![]() ( )
( )
(recall that O lags behind E).
The difference
between those numbers should be ![]() for the half wave condition to be met. Thus
for the half wave condition to be met. Thus
![]() ( )
( )
or, equivalently
![]() . ( )
. ( )
It results
![]() , ( )
, ( )
which is too small to
obtain in practice. Fortunately the condition ![]() also works if we add multiples of 2π to
the difference in phase. The next thickness is thus obtained from the condition
also works if we add multiples of 2π to
the difference in phase. The next thickness is thus obtained from the condition
![]() . ( )
. ( )
Then the next possible thickness of the half-wave plate is
![]() , ( )
, ( )
which is still too small (about a tenth of the thickness of human hair), but we can continue the procedure until we find a practicable thickness.
Quarter wave plates
Similarly,
quarter wave plates introduce a difference in phase of ![]() between ordinary and extraordinary waves or,
equivalently, a difference in optical path of
between ordinary and extraordinary waves or,
equivalently, a difference in optical path of ![]() .
Recall that by superimposing linearly polarized waves of the same amplitude
which are out-of-phase by
.
Recall that by superimposing linearly polarized waves of the same amplitude
which are out-of-phase by ![]() ,
circularly polarized light is obtained. So, a quarter wave plate
produces circularly polarized light on two conditions:
,
circularly polarized light is obtained. So, a quarter wave plate
produces circularly polarized light on two conditions:
1) the incident light is linearly polarized;
2) the amplitudes of the oscillations in the extraordinary and
the ordinary wave are equal (this can be done by taking ![]() ).
A device designed to circularly polarize light is composed of a linear
polarizer and a quarter wave plate.
).
A device designed to circularly polarize light is composed of a linear
polarizer and a quarter wave plate.
The birefringence of crystals is used in several devices as the Nicol prism or the Wollaston beam polarizing splitter. In the figure below, a Nicol prism is presented.
O-ray E-ray
![]()
![]()
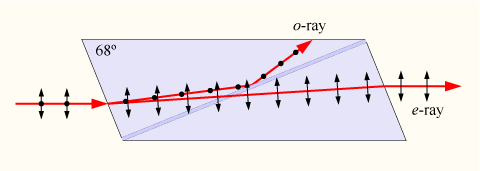
It is made of
calcite and consists of a rhombohedral crystal which is split diagonally. The
parts are consequently joined together using Canada balsam (![]() ).
The ordinary wave is incident at the calciteCanada balsam interface under an
angle higher than the critical angle
).
The ordinary wave is incident at the calciteCanada balsam interface under an
angle higher than the critical angle ![]() for total internal reflection (recall that
for total internal reflection (recall that![]() ).
The O-ray is thus totally internally reflected. Because it sees a refractive index less than 1.53,
(recall that
).
The O-ray is thus totally internally reflected. Because it sees a refractive index less than 1.53,
(recall that ![]() )
the E-ray is transmitted at the calciteCanada balsam interface and leaves the
Nicol prism through the side opposite to the entrance side. It will have a vertical
state of polarization.
)
the E-ray is transmitted at the calciteCanada balsam interface and leaves the
Nicol prism through the side opposite to the entrance side. It will have a vertical
state of polarization.
A Wollaston polarizing beam splitter is made of two quartz prisms connected together with glycerine. The optical axis of the first prism parallel to the entrance interface of the device and the optic axis of the second prism is perpendicular to the plane of incidence.
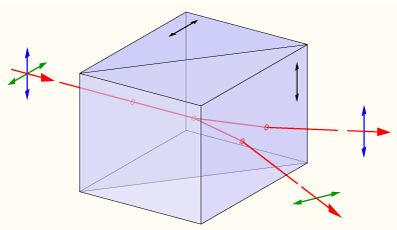
The O and E beams
travel together in the first prism due to the direction of propagation with
respect to the optic axis. On crossing the diagonal interface the E wave, which
is polarized perpendicularly to the optic axis of the second prism, becomes an
O wave. Since for quartz ![]() ,
the O wave in the second prism bends away from the normal.
,
the O wave in the second prism bends away from the normal.
On the other
hand, the O wave in the first prism becomes E wave in second prism and bends
toward the normal. The result is that incident unpolarized light is split into
two polarized beams. The angle of divergence of the emergent rays depends on
the wedge angle of the prisms and for commercial devices the latter varies
between ![]() and
and ![]() .
.
The sunlight is unpolarized. However, when it crosses atmosphere sunlight gets partially or totally polarized. This happens because incident unpolarized light sets the molecules in charges to reradiate light with directions of polarization related to the direction of acceleration of charges.
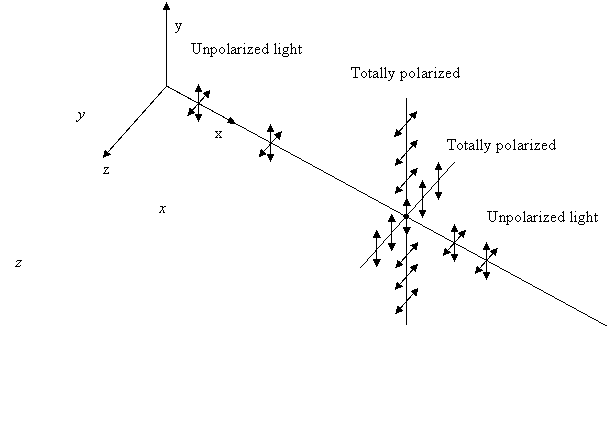
As you can see from figure above, light which is scattered at an angle of /2 is totally polarized. Light
scattered at angles smaller than /2
is partially polarized. Light scattered in the forward direction is
unpolarized.
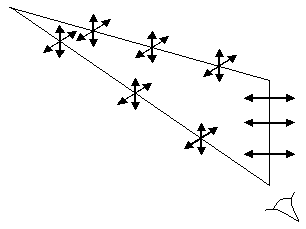
As a consequence, light coming from the sun at dawn or at sunset is unpolarized. Light above the head of the observer at daytime is totally horizontally polarized. Light which comes from the sun is partially polarized. This phenomenon causes the polarized sunglasses to be more effective than ordinary unpolarized glasses. The direction of transmission of polarized sunglasses is always vertical.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2558
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved