| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
Necessity, Worlds, and Chance
The conceptual framework in terms of which we have been operating points to the following definition of natural law: A natural law is a universal proposition, which holds in all histories of a family of possible histories. . . .
Concepts as Involving Laws and Inconceivable without them.
Wilfred Sellars, p. 309.
The accounts of laws of nature to which we shall now turn, I call necessitarian. For in these accounts, unlike in Lewis's, necessity comes before law in the order of definition. They are also less ambitious, for they do not attempt to characterize necessity and laws by means of commonly understood relations between theory and fact. Instead they begin with a substantial assumption of reality: the reality of other possible worlds besides our own. I shall begin with a critical assessment of that assumption; thereafter I will mostly grant it for the sake of argument.
This chapter will focus also on physical probability, which gives a new shape to the idea of law. This will introduce questions which, I maintain, necessitarian accounts cannot answerquestions which we shall confront again later, however, for they arise today for any philosophy of science.
Are There Other Possible Worlds?
Since realism about possible worlds will now play such an important part, I propose a suspension of our disbelief for most of the discussion. But here, and finally again at the end, I shall briefly examine this realism and its support, and outline (even more briefly) the corresponding anti-realist stance.
The recent respect for possible worlds derives from their use in semantics. Let us first see how they are used there, and then consider an argument for their real existence.
Modal terms like necessarily, possibly, actually obey certain logical rules. The venerable modal square of opposition (see Fig. 4.1) summarizes the main ones. The vertical arrows signify implication or valid inference. For example, as the medievals codified it: necessity implies actuality and actuality implies possibility. The diagonal lines marked cont link mutually contradictory propositions: each is exactly the other's denial. Cntry means that the linked statements are contraries (could not both be true), and subcntry that they are subcontraries (could not both be false). To know this diagram is to have a very good initial grasp of the valid inference patterns in modal discourse.
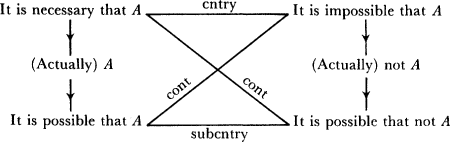
Fig. 4.1. The
This understanding about arguments is thus available before we have asked, what the conditions are under which modal statements are true. A semantic theory will answer that question, at least at some level of generality. The answer it gives must bear out the correctness of the above square of oppositionthat is, a semantic theory must save the phenomena of inference! And a clue to how to do this has also been available for many centuries: it is the similarity of the above diagram to the quantifier square of opposition (see Fig. 4.2). Here an assumption is clearly present: something, correctly designated as This B, exists.
The following theory now suggests itself. There are other ways the world could have beenbriefly, there are possible worlds, the actual one and some others. Actual is like this, necessary like all, and possible like some. To be precise, call a world an A-world exactly if proposition A is true of it. Then Fig. 4.3, which is a specific instance of the quantifier square of opposition, indicates clearly how to translate modal discourse into discourse about possible worlds. This is a graphical summary of the truth-conditions
end p.66
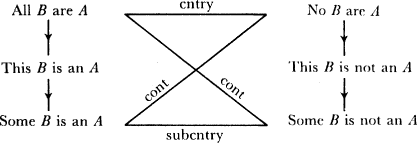
Fig. 4.2
for modal language which the semantic theory presents. Thus It is possible that there are chimaeras is true if and only if there are possible worlds of which There are chimaeras is true, or more perspicuously, There are possible worlds in which there are chimaeras, is true.
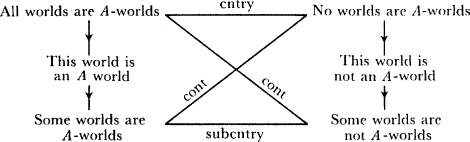
Fig. 4.3
This semantic theorystandard reference, truth, and possible world semanticswas greatly elaborated beyond the initial stage. In the 1960s and early 1970s especially, it went from success to success in philosophical logic, and theoretical linguistics. Consider now the argument:
|
1. |
There is a proposition A such that both It is possible that A and It is possible that not A are true. |
|
2. |
There are at least two possible worlds. |
|
3. |
There is at least one other possible world, besides the actual one. |
The first is a premiss offered for your acceptance. The second follows then by the above semantic theory (given 1, there must be an A-world and also a world which is not an A-world). The
end p.67
conclusion 3, which follows from 2, expresses exactly the view we call realism about possible worlds.
Let's not quarrel with the premiss, but ask instead how we get from 1 to 2. This step is made on the basis of a semantic theory, and that theory, as we said, has been very successful. But what sort of success did it have? Did it lead to predictions, that could be checked by observation? To suggest that the answer is Yes (also for their other theories) adherents began to use predict as a synonym for imply or even for allows for. But the predicted phenomena are, in any case, all about how people speak, and about what they regard as grammatical, correct, tautological, valid, or alternatively, invalid or absurd. The phenomena saved, if any, are the accepted patterns of inference in a certain area of discourse.
Is this sort of success sufficient to force us from an acceptance of 1 to acceptance of 2? I will not argue the point here, but will just say that it does not seem sufficient to me. 1 The alternative point of viewa modal anti-realismis that the success of the semantic theory consists in providing us with a family of models of discourse. Possible-world talk can then be combined with the robust denial that there are other possible worldsfor possible-world talk is then only a picturesque way to describe the models. Realism with respect to possible worlds asserts that these models do more than demarcate valid from invalid inferencethat in addition, each element of the correct model(s) must correspond to an element of reality. To this reification of models I shall return in the last section.
2. Laws Related to Worlds
Law implies necessity: if it is a law that wood burns when heated, then wood must burn when heated. This traditional connection was also elaborated so as to make it stronger: the law is the reason for the necessity, the necessity is there because of the law, and not conversely. The terms reason and because are mysterious, however. It is not clear whether something could be necessary without following from a lawthe directedness of because may or may not be reflected in that of implies.
David Lewis, as we saw, simply equates being (physically) necessary with being (implied by) a law. That equates law with
end p.68
necessity, since on his account whatever is implied by laws is also a law. In this course he was not egregious. Reichenbach defined a fact P to be physically necessary exactly if the sentence describing P is a nomological sentence in the wider sense, the indicated class of statements being intended to consist of laws of logic, laws of nature, and their consequences. A few years later Fitch defined the corresponding modal connective It is naturally necessary that to mean It is (logically) necessary that if L then where L stands for, he says, the conjunction of all laws of nature. Montague's treatment in 1960 presented a corresponding semantic characterization. The form of presentation in all three cases clearly shows that the authors take themselves to be merely making precise a common notion. 2
The important innovation that gave flexibility to possible world semantics was Saul Kripke's insight that the same square of opposition which fit bare necessity:
|
1. |
Necessarily A is true in world x if and only if A is true in all worlds |
would also fit any restricted necessity:
|
2. |
Necessarily A is true in world x if and only if A is true in all those worlds which are possible relative to x. |
Here possible relative to is a relation, of whatever character. We require only that it be reflexiveany world x must be possible relative to itself. For then it will follow that if Necessarily A is true, so is A itself, regardless of which world we focus our attention on.
The relation of relative possibility is also called the access relation, in which case 2 takes the form
|
2′. |
Necessarily A is true in x exactly if A is true in each world to which there is access from x. |
But what is this relation, and what is it like? It is instructive to look at this a little more, from the point of view which defines necessity in terms of law. It appears that we have three candidates for the relation of (physical or nomological) relative possibility. Each will give rise, via equation 2, to a distinct sense of (physical or nomological) necessity:
World y is possible relative to world x exactly if:
|
R 1 : no law of x is violated in y |
end p.69
|
R 2 : every law of x is also a law of y |
|
|
R 3 : y has exactly the same laws as x. |
These three relations have different characteristics. It must follow from what is meant by law that a law of x is not violated in x, so all three relations are reflexive (x bears R i to x). The second and third are also transitive, and finally, the third is in addition symmetric. Among the earliest results of Kripke's pioneering work we find that the logic of Necessarily obeys three distinct, previously studied logical systems in these three cases. The differences between them come out only when we place modal phrases within each other's scope, as in It is necessarily the case that it is not necessary that . . . Philosophers, unlike logicians have largely ignored the complexities of such nesting at least in discussions of physical necessity.
So far I have followed the pattern, also used by Lewis, of characterizing necessity in terms of law. But now we must ask the question: can we invert this order, and define the notion of law in terms of such notions as those just introduced: worlds, and relations among worlds?
It will take the remainder of this chapter to arrive at an answer; but here I shall chart the main alternatives.
In 1948, Wilfrid Sellars introduced the use of Leibniz's metaphysical story of possible worlds into the twentieth-century discussion of laws and necessity. 3 His paper raises the most important issues involved and gives a precise formal treatment foreshadowing the now familiar possible-world semantics. Of course, Sellars was acutely aware of Kant's impact on the metaphysical problmatique, and characterizes what he does as a philosophically useful exploration of nave realism (p. 302). The writers who followed himthough perhaps unaware of his workmostly did not share this attitude.
The simplest sort of analysis of law, of this sort, merely postulates that (a) there are possible worlds, (b) there is a relation of relative possibility between them (the access relation). The definition then follows: it is a law of world x that A if and only if it is true that A in every world which is possible relative to xi.e. exactly if It is necessary that A is true in that world. Special postulates may then be added, to describe the access relation, and say that it is reflexive and so forth. This analysis was proposed by Robert Pargetter. 4
A somewhat more complex sort of analysis would require some special features for any proposition A to be a law, in addition to its necessity. Such a special feature could be universality, explained in one way or another. An alternative sort of sophistication could lie in attempts to relate the access relation to features of the worlds themselves, such as their history. An analysis with both sorts of elaboration has been developed in a number of publications by Storrs McCall. 5
I did not raise the issue in the preceding chapter, but a special effort is needed to accommodate probabilistic laws. This has become crucial, since physics now includes irreducibly statistical theories. The assertion that a radium atom has a 50 per cent probability of decaying within 1600 years, does not have the form that something specific must happen, or even will. Thus at least the simplest type of possible worlds account will not work for them. Peter Vallentyne (and also McCall) draws on theories of objective chancenotably David Lewis'sto generalize the necessitarian notion of law. 6 He does so in the framework of possible-worlds models incorporating time, along McCall's lines.
There are important differences between the accounts of law and necessity given by Pargetter, McCall, Vallentyne, and other authors who have explored this avenue of approach. Some of these differences are of merely technical interest, others are more philosophical. I must emphasize, with apologies, that I shall not try to replicate their individual accounts. I shall only try to explore general alternatives, and to show that there are two problems that beset all of them. Both concern the relation of model to reality. In later chapters I will detail how I recognize a legitimate place for possible-worlds models, and how their use can be meaningfully integrated into the epistemic process. But what I say there will not require that we have a way of referring to real, unactualized possibilities, or to one (purportedly denoted, but undescribed) relation among them, or that every element in the model used have a counterpart in reality. However that may be, the metaphysical accounts of laws of nature, based on realism about possible worlds, have their own peculiar problems, to which we now turn.
end p.71
3. The Identification Problem
Here is the simplest necessitarian account. There really are possible worlds; which is not to say that all logically and consistently describable worlds are among them. Perhaps there are worlds in which pigs fly, or in which Bertrand Russelllike Jourdain's R*ss*llwas torn apart by suffragettes; but perhaps there are not. Secondly, there is a relation of relative possibility between worldsthe access relation. To say that a proposition is a law in a given world is the same as saying that it is necessary in that world. It means that this proposition is true in all worlds which are possible relative to that given world.
As Pargetter, who proposed such an account, explicitly recognized, we are immediately faced with a problem. Which relation among worlds is that relation of relative possibility? Since law is now a derivative notion, it cannot be used to identify the access relation. Calling it the relation of relative possibility also does not help: this is to baptize it in absentia, so to speak.
Certain characteristics of that relationship may be postulated, for example that it is reflexive. If we make the list of postulates long enough, will that single out a unique relation? No, it won't, unless it is one of those trivial relations which either hold between all worlds or between none. Otherwise we can always find a distinct, isomorphic relation, which satisfies the same postulates. (Indeed, metalogical results teach us that if there are infinitely many worlds, there will also be non-isomorphic relations that fit.) We can't single out the relation by description; and obviously we also can't by pointing to it. This is the identification problem.
Suppose that when I say that there is a law of gravity, I mean that something or other is true about the access relation. If I don't know what relation that is, then I don't know what I'm saying.
Pargetter proposes a solution. The solution is again anti-nominalismthe realist position concerning classes to which Lewis also turnedbut with respect to relations among worlds. To the mathematical mind, a relation is simply a class of pairse.g. kinship is the class of pairs x, y such that x is a kin of y. But not all classes correspond to real relations. A natural class of pairs does, and an unnatural class does not. There is, says Pargetter, only one real relation among worlds. So there is no problem about identifying the access relation. It is the only one there is.
end p.72
He need not have been quite so radical. After all he had postulated some characteristics for the access relation. So to solve the identification problem he need only add to his postulates: and there is only one real relation among worlds which has these characteristics. That does not mean that he has given us a complete or even very informative list; the extra postulate would only be that the list contains enough information to identify the access relationas fingerprints might identify a murderer.
Before turning to less simple necessitarian accounts, let us see where we now stand. First consider the person who decides to believe the above account, including some such postulates as Pargetter's. Suppose in addition that he believes that what science says is our best guess at what the laws of nature are. This person has of course no difficulty (in principle) in finding out what the access relation is like. Every bit of science he studies will tell him a little more. There is a problem of under-determination: he will never learn enough to identify the access relation by description. But that's why he has his postulate: if we ask him what relation he is talking about, he can say But there's only one.
For those of us who do not believe this postulateeither because we have some little doubt about the reality of other worlds, or because we believe in worlds, but are not anti-nominalists of the same sortthe situation is a little hopeless. We don't know what he is talking about.
Could we finesse our communication difficulties in some way? Suppose we translate his utterance It is a law that A as There is a relation R among worlds, which has all the properties he has explicitly laid down, and it is the case that A in every world which bears R to ours. Then, if we take all classes of pairs to be real relations, we have trivialized his assertionit has lost all informational value for us. If on the contrary we say that only some classes of pairs are real relations, but we don't know which, we are back in our original quandary. We have to ask him: if there are several such relations, what distinguishes the one you are talking about from the others? And he has no reply except the, to us so unsatisfactory, But there's only one.
So far the simplest necessitarian account. Let us see if more sophisticated variants fare better.
end p.73
4. Time and the Branching Universe
The identification problem would be solved entirely if the access relation could be defined, in terms of characteristics of the worlds themselves. Since the access relation determines all modal facts, the definition would have to be in terms of what actually happens and actually is the case in each worldin other worlds, in terms of their histories.
There are many possible worlds whose history is the same up
until now. They too started with a Big Bang, or were created in 4004 bc (as
This picture of a settled past and open future perennially contends, in our ontology, with the view of history sub specie aeternitatis, from beyond the end of time so to say. In the former, the past has gained its own unalterable necessityWesen ist was gewesen istbut determines the future only within certain limits. Prevision is but guessing; what we see has already turned to stone behind us.
A Klee painting named Angelus Novus shows an angel looking as though he is about to move away from something he is fixedly contemplating. His eyes are staring, his mouth is open, his wings are spread. This is how one pictures the angel of history. His face is turned toward the past. Where we perceive a chain of events, he sees one single catastrophe which keeps piling wreckage upon wreckage and hurls it in front of his feet. 7
Besides this angel there must be another, facing forward, his face shining with hope as he beholds the embarras de richesse of possibilities in our open future. 8 But let us see how this view of time and history could aid the necessitarian programme for explicating law of nature.
The identification problem may be solved if we define relative possibility in terms of shared history. 9 Call two worlds x and y t-equivalent exactly if they have the same history through time t. Thus, at time t, they share their entire past and present. This is a
end p.74
defined relation among worldsthough one that is time-indexedand we can take it to be the access relation. The corresponding sense of necessary is customarily expressed by another word, settled. The worlds which are t-equivalent to world x together form the t-equivalent of x, or as we can also say, the future cone of x at t. We can illustrate this as in Fig. 4.4. The worlds y, x, w belong to the t-cone of x; and all those, plus z and v, belong to the t-cone. The other worlds w′ and v′, which share no history with x, do not belong to either cone.
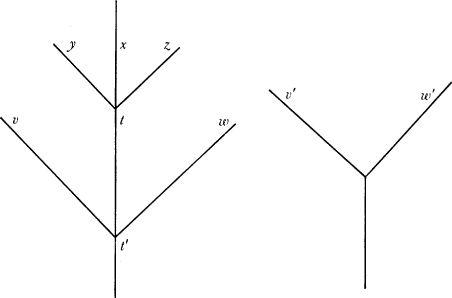
Fig. 4.4 Possible-World Histories
|
Definition. |
Proposition A is settled in x at t if A is the case in every world which is t-equivalent to x (i.e. every world in the t-cone of x). |
This being settled is a kind of necessity, for if it is settled that A, that means that A is true regardless of how our future develops, no matter how history goes from now on.
What we have now introduced is certainly well enough defined, but does it give us the access relation needed for an account of laws? There are two reasons why it cannot. First of all, it is clear that if it is settled that A, it is still not generally true that it is a law that A. Many facts have been settled by what we call the accidents of history. This can be so even though A concerns the futureit may have been settled by 1900 that the twentieth century would see the devastating effects of population explosion, world wars, and social disease. To say that this was settled means that certain alternative possible futures were ruled out, could no longer come into being, after 1900. Even if that was due in part to laws of nature, it was partially due to what had happened already.
To eliminate the element of historical accident, we could require what is a law now to be not only settled now, but to have already been settled at all times in our past. Let us call that fully settled:
|
Definition. |
Proposition A is fully settled in x at t if A is settled in x at every time t′ ≤ t (at which world x already existed). |
(See Proofs and illustrations for a further discussion.)
But what the laws are, cannot be the same as what is fully settled. For that would mean: if two worlds had the same history for their first two minutes, or two seconds, or two nanoseconds, . . . they would have the same laws of nature. But the facts do not, and cannot, determine what the laws arecertainly not to that extent. The intuitive concept of law requires that there are other laws this world could have had, that would allow at least a short epoch of identical initial conditions and development.
This is a very telling problem. We realize now that we can't even say that if something is a law then it is settled that it is a law. For if it is a law, then it won't be contravened in any possible future that is allowed by our laws. It may be violated only in some possible future, belonging to a world that is just like ours till now, if that world is subject to different laws. This realization puts a complete stop to the idea that we could solve the identification problem by defining the correct access relation in terms of shared historical structure.
Indeed we have now ruled out another option along the way. We also cannot hope to characterize the laws as a special class of settled propositions. But as we have seen, something can be a law, and not settled. That is shown by the example of two worlds x and y which have, say, the first two minutes of history in common, but have different laws of nature. For example, in x but not y it is a law that A; no part of x's future violates A but some part of y's
end p.76
future does. Then it is not settled that A in x or y, during those first two minutes.
We have thus seen that the sense of necessity appropriate to laws does not even imply that of being settled (let alone fully settled) and hence also cannot be defined as a special case thereof. I wanted to explore this very fully, so that the hope of seeing nomic necessity explicated in terms of the structure of branching histories would not remain hovering in the background. 10
McCall and Vallentyne both speak of a special nomic necessity and indicate that this does not supervene on the historical structure which they describe; so they cannot be accused of a lack of insight here. But that does mean that they are in no better position with respect to the identification problem. Which necessity is nomic necessity? Each necessity can be defined in terms of an access relation among worldsbut which is the nomic access relation?
Proofs and Illustrations 11
The model of possible worlds developing in time has three
basic ingredients: Timewhich I will here take as represented by the real
number continuum ![]() ; the
set of worlds W; and the set of states that worlds can have at a given
momentI'll call that K. Each world x has a history: a function s
which gives world x an instantaneous state s(x, t) at time
t, during a certain interval T. That state is the location of x
at time t in the state-space K, and s(x, −)
has as graph the trajectory of this world in that space. Fig. 4.4, which
looks like a tree, shows a number of such trajectories, plotted against time;
the limitations of the printed page require K to be represented there by
the straight horizontal line which is not drawn at the bottom.
; the
set of worlds W; and the set of states that worlds can have at a given
momentI'll call that K. Each world x has a history: a function s
which gives world x an instantaneous state s(x, t) at time
t, during a certain interval T. That state is the location of x
at time t in the state-space K, and s(x, −)
has as graph the trajectory of this world in that space. Fig. 4.4, which
looks like a tree, shows a number of such trajectories, plotted against time;
the limitations of the printed page require K to be represented there by
the straight horizontal line which is not drawn at the bottom.
A proposition is identified by the set of worlds in which it is true. We may call a proposition historical if its truth-value is determined by a world's historyi.e. if two worlds have the same history, then such a proposition is either true in both or true in neither. The model allows for non-historical propositions as well, but they can't be represented in such diagrams.
Strictly speaking, a proposition is simply true or false in a world, and it does not make sense to say that something is true at one time and not at another. But the less strict way of speaking is easily explained. It is true of world x that it has state s(x, t) at t. If s(x, t) is inside region K′ inside k, we can similarly say that x is inside K′
end p.77
at t. The proposition which is true in a world y exactly if s(y, t) is inside K′, can be very perspicuously be written K′(t), and the propositional function K′(−) may be called a (temporal) proposition which can be true in world x at one time twhen s(x, t) is in region K′and false at another. And finally, any proposition which is not historical at allfor example, that the world was created or 2 + 2 = 4may be said to be true at all times if it is true at all, and false at all times otherwise.
Suppose now that A is fully settled in x at t. That means that A is settled in x at all t′ ≤ t. Now take an arbitrary time t * at which x exists. If t * ≤ t, then it follows automatically that A is settled in x at t *. If t * ≥ t, could A be not settled at t *? That would require a world y, whose history is the same as x through t *, in which A is not true. But that world y has a history which is a fortiori the same as x's history through t, so that would imply that A was not even settled at t. Therefore we see that if A is fully settled at t, then it is settled at all times. But that entails in turn that it is fully settled at all times. (Henceforth we can just say fully settled, and leave out at time . . . .)
It follows now that if x and y share any initial segment of history, then what is fully settled in the one is so in the other. For let A be fully settled in x, and let y be in x's t-cone, for any time t, even at the very beginning of their history. This means that A is settled in both x and y at all times ≥ t, sincehaving the same history so farthey have the same future cones, at least through time t. But then A is fully settled in y at t, and hence, as we have seen, at all times.
5. Probability: Laws and Objective Chance 12
Radium has a half-life of approximately 1600 years. That means that half of an initial amount of radium decays into radon, within 1600 years. 13 For an individual radium atom, the decay is a matter of probability. It has a 50 per cent probability of remaining stable for 1600 years, 25 per cent for 3200 years, 12.5 per cent for 4800 years, and so on. The general law has the form
|
P(atom stable for an interval of length t) = e − At |
where A is the relevant decay constant. This shows how the
end p.78
progression works: e − A2t is
the square of e − At , so probability ![]() over
1600 years becomes
over
1600 years becomes ![]() over
3200 and so forth.
over
3200 and so forth.
Physics gives us such statistical information, and in contemporary physics the probabilities are essentially irreducible. That is, they cannot be regarded as merely measuring our ignorance of factors which really determine the exact time of decay beforehand. With this probabilistic turn in science, the discussion of laws suited in form to deterministic worlds only, becomes inadequate.
What if, as in the preceding section, we attempt to see this in terms of what our possible futures may bring? Intuitively, the atom decays within 1600 years in half of these possible futures. Hence we can suggest that the real probabilityobjective chance as opposed to our subjective likelihoodis a measure of proportion among the possible worlds which share our history so far. Greater objective chance of happening actually, means really happening in more possible futures.
Unfortunately the identification problem now reappears in an especially striking and difficult form. If our possible futures are only finitely many, perhaps it could be insisted that each is equally likely (though, why?) and that calculation of chances should proceed on that basis. If they are infinitely many, but only countable, they cannot be equally likely. For their probabilities must add up to 1 (i.e. 100 per cent), and any number, greater than zero, becomes greater than 1 if added to itself sufficiently often. And finally, if they are infinitely many and form a continuum (surely the most plausible idea) then it literally makes no sense to say: the objective chance is the measure that treats them all as equally likely.
Let me explain that. I do not mean simply that each individual future, in such a continuum, must receive probability zero. That is so, but that does not rule out a positive probability for, for example, the class of futures in which this atom decays within 1600 years. However, to give each individual point in the continuum the probability zero, treats them equally but leaves open entirely what the probability of such a class shall be. Fig. 4.5 represents various probability distributions over a continuum of possible worlds. We see curves C 1 , C 2 , C 3 and I define probability measures P 1 , P 2 , P 3 to assign a number to any class of worlds represented on the horizontal line, by their means. Measure P i gives to class A j a number proportional to the area above A j but below curve C i . Now each such measure gives zero to every individual point (world), but
end p.79
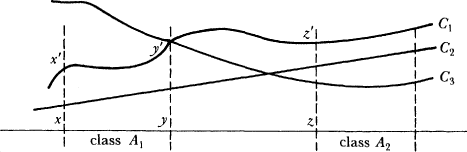
Fig. 4.5
they disagree very much otherwise. According to one, class A 1 of worlds is larger (has greater probability) than class A 2 , and according to another, it is smaller.
In the diagram, classes A 1 and A 2 are represented by equal intervals on the horizontal line that represents the worlds. Should they therefore receive equal probability? But that makes sense only if we have a measure of distance between worlds, which is of course no easier to come by. I could have just as well described the diagram differently, and said that the points on curve C 3 represent the worlds. Why should the distances between x, y, z be a more faithful representation than those between x′, y′, z′ above them?
To have a way of representing chance, as a measure on the possible futures, is nothing. That we can so represent it is a trivial logical fact, and helps not at all to tell us what chance is, or what the real chances are. Which measure is chance?
Two courses seem open here. We can say that it is something quite different, and independent of the world histories. In that case, we must add some move like Pargetter's to close the identification gap. Needed is an anti-nominalism, in the very specific form of a postulate which says: there is only one real measure function on the possible futures, and the remainder are mathematical fictions.
The second course is to look into past history, and identify factors in terms of which chance can be identified. This would be like the attempt to define the relative possibility relation in terms of shared history. We would have at once what I noted as a problem before. If world history is only two minutes old, say, does what has happened already determine uniquely all the objective chances of everything that could happen later? Are there really no two worlds, agreeing on the first two minutestwo seconds, two nanosecondsof history, but disagreeing in objective chances for their future?
We can certainly postulate that chance supervenes on actual historyincluding of course the structure of the substances involved therein. But this supervenience will be an illusory gain if it is via a lawsuch as the law that if an atom has a certain structure then its chances of decay are thus and so. For as we saw before, the identification problem for non-probabilistic laws could only be solvedif solved is apt at all!by sheer postulation. Merely to postulate that chance supervenes on history or structure, without saying how, would of course also be no help at all in identifying chance. Nevertheless, there are two things we cannot forbid. One is to postulate that chance, though not identifiable, is real. The other is to postulate, in anti-nominalist fashion, that only one probability measure on the possible worlds or histories is real, so that identification is easy by fiat. But then we must ask whether this newly introduced notion, about to bear the entire weight of the concept of probabilistic law, can do its job. That will turn out to be surprisingly difficult.
6. The Fundamental Question About Chance
How and why should beliefs about objective chance help to shape our expectations of what will happen?
This is the fundamental question about the concept of chance. 14 I am going to argue that within the metaphysical point of view, the question cannot be answered at all.
Indeed, in this context, that question about chance appears as a generalization of the inference problem: show that on the advocated account of laws, the assertion It is a law that A entails A. That this must be shown follows from the most minimal criterion concerning how law relates to necessity. Neither David Lewis's nor the necessitarian accounts of law have any difficulty with it in this form. (Matters will be otherwise for universals accounts, examined in the next chapter.) However, once we begin to look at probabilistic laws, and necessity is generalized to chance, we must pose the problem in a new and more general form.
The assertion that there is an objective chance of 50 per cent that a radium atom now stable will decay within 1600 years, does
end p.81
not imply that it will actually do so. What information does it give us then about what will happen? Or, if that question cannot be answered without repeating the assertion itself, let me rephrase what we need to know: how and why should beliefs about objective chance help to shape our expectations of what will happen?
Probability has two faces. 15 On its subjective side, probability is the structure of opinion. But when physics today tells us the probability of decay of a radium atomfor exampleit does not in the first instance purport to say something about opinion, or to give advice, but to describe a fact of nature. This fact being a probability, we are looking upon probability's objective sidephysical probability, or objective chance.
There must be a connection between the two. Given that the objective chance is thus and so, my opinion must follow suit, and I must align my expectations accordingly. This summary of the connection between the two is generally called Miller's Principle:
|
(Miller) |
My subjective probability that A is the case, on the supposition that the objective chance of A equals x, equals x. |
|
Symbolically: P(A|ch(A) = x) = x |
This is meant to hold for me, or anyone whose opinion is rational, and who grasps the concept of chance. 16
Principles of rationality can at times be warranted by coherence arguments. Their general form is: if someone does not form his opinion in this way, then he is sabotaging himself, even by his own lights. But how could we have a coherence argument for Miller? The coherence would have to be between opinions about what will happen, and opinions about chancebut then the latter would have to include opinions about the connection between chance and what happens.
It is not easy to see what those opinions could be. If a coin is fair, then the objective chance that it comes up heads if tossed, equals 50 per cent. We should like to infer something about how often it will come up heads if tossed repeatedly. But of course, it may come up tails every time. And if it does come up tails, say ten times, the objective chance of its coming up heads on the eleventh toss is no greaterto think otherwise is the gambler's fallacy.
We appear to have two alternatives here. The first course is to deny my cavalier of course, it [the fair coin] may come up tails
end p.82
every time. That is, we could propose an account of chance that identifies it, or links it very intimately, with actual relative frequency. The second course is to accept the possibility of radical divergency between chance and actual frequency, but show that it is not likely.
The first course I shall not discuss here. 17 It does not fit well with the concept of chance as generalized from that of law. Laws are meant to explain regularities, hence they can't be (mere) regularitieson that the tradition insists. Similarly then, chance is meant to explain frequency (and statistical correlation in general) so it cannot be (mere) actual relative frequency.
The second course faces the immediate question: which face of probability does likely signify here? If it means subjectively likely, we have simply restated Miller's Principle. But if it means objectively likely, how would that get us any farther? There is in fact a beautiful general theorem concerning probability in any of its senses: The Strong Law of Large Numbers. Let me explain its implication for the example of coin tossing, and then see if it helps us.
Suppose a coin is fair, and each toss is independent of all
other tosses. I take fair to mean that the objective chance of heads
in any one toss equals ![]() .
.
Now this entails at once an objective chance for getting two
heads in two tosses, namely ![]() .
In just the same way it entails an objective chance for getting exactly two heads
in three tosses namely
.
In just the same way it entails an objective chance for getting exactly two heads
in three tosses namely ![]() and
for getting no heads at all in ten tosses namely
and
for getting no heads at all in ten tosses namely ![]() .
What is the objective chance, so calculated, of getting tosses half the time,
in the long run, if you keep tossing forever? The answer, according to our
theorem, is 1, that is, 100 per cent; total objective certainty that objective
chance and long run frequency are the same.
.
What is the objective chance, so calculated, of getting tosses half the time,
in the long run, if you keep tossing forever? The answer, according to our
theorem, is 1, that is, 100 per cent; total objective certainty that objective
chance and long run frequency are the same.
Could this result warrant Miller's Principle? Not at all,
unless we assume that our expectations should be based on this 100 per cent
objective chance. But the question at issue was exactly: what makes it
rational to base our subjective expectation on our beliefs about our objective
chance? A theorem, which assumes only that objective chance is a
probability measure (and extends the measure from individual events to
sequences) simply cannot answer such a question. After all there are many
probability functions; suppose that the probability 1 that the coin
comes up heads on any one toss equals ![]() ,
and that the probability 2 of its doing so equals
,
and that the probability 2 of its doing so equals ![]() .
Then the theorem tells us that there is 100 per cent probability 1
that it
.
Then the theorem tells us that there is 100 per cent probability 1
that it
end p.83
will come up heads half the time in the long run, and also 100 per cent probability 2 that it will come up heads one-third the time in the long run. These corollaries to the theorem give no guidance as to whether I should base my expectation on my beliefs about probability 1 or on those about probability 2 .
Returning now to the McCallVallentyne programme for explicating laws of nature, in which objective chance is conceived as a kind of graded necessity, we can pose the inference problem very concretely. Suppose chance is a sort of proportion among our possible futureswhat does it have to do with frequency of occurrence in our actual future? In this form I call it the horizontalvertical problem because of its pictorial illustration (see Fig. 4.6).
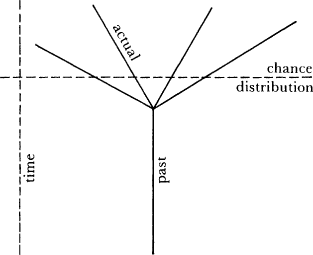
Fig. 4.6. The HorizontalVertical Problem
Relative frequency is measured by counting along the vertical line which represents our actual history. But chance is a distribution over the horizontal dotted line, which represents the spread of possible worlds. So how could one possibly show that the one should help to determine the other?
This sort of problem has two interesting historical aspects in physics. In nineteenth-century statistical mechanics it appears as the ergodic problem, which is to relate the equiprobability metric of MaxwellBoltzmann statistics to the proportion of sojourn times in a system's trajectory. The problem was solved by the development of ergodic theory in the twentieth century. But the solution takes
end p.84
roughly the form: under certain special conditions, which may or may not be realized in nature, the ergodic hypothesis is correct. 18 In addition, those conditions concern the probability measure in question. Hence we would have the same problem as with the Law of Large Numbers if we tried to appeal to the ergodic theorem to establish a relation between the two faces of probability.
The second place we see such a problem is more obviously connected with the present context: it is in the EverettDeWitt many-worlds interpretation of quantum mechanics. Quantum mechanics is an indeterministic theory in some sense: it gives us irreducible probabilities for measurement outcomes. On the many-world interpretation, whenever a measurement occurs, each of the possible (mutually incompatible) outcomes actually occurs, but in a different possible world. The world we are in splits. This is exactly the sort of story we have just been hearing from McCall and Vallentyne. But for Everett and DeWitt this takes a very concrete form, which derives from the Hilbert space models of quantum mechanics. 19
One of the advantages that was claimed for the many-worlds interpretation was that the rule (Born's rule) for calculating probabilities of measurement outcomes would be derivable. The derivation was supposed to show that the numbers assigned by this rule were exactly the relative frequencies to be expected (for the measurements in question) in the actual world. Since it is easy enough to see a probability function for this sort of situation, as it were encapsulated in the quantum mechanical state, we can see what this claim amounts to: it is exactly the claim that the horizontalvertical problem has here a demonstrable conclusion.
In actual fact, however, this topic constitutes one of the failures of the many-worlds interpretation. The purported derivation of Born's rule was from premisses, in addition to the mathematical description of the quantum mechanical state, which smuggled in the conclusion itself. The horizontalvertical problem was solved by assumptive fiat. 20
These sidelights on recent history of physics thus only underline the seriousness of this horizontalvertical problem. It appears that if the metaphysical point of view is maintained, in which the problem arises in this form, then no solution is possible.
I do not want to leave this as an open question. There is no way at all to answer the fundamental question about chance within the present confines. For consider the options. First of all as I noted, no coherent argument could justify the principle, since it would have to rest on premisses about rational opinion of chancebut Miller's Principle is the basic such premiss. Secondly, as David Lewis noted at the end of his Subjectivist Guide, the Principle would be derivable if both rational opinion and chance derived from a single objective probability measure. That measure could only be what Carnap called logical probability, the unique probability that respects all principles of logical symmetry (indifference). But there is no such unique measure (as we shall see in Part IV), therefore logical probability does not exist. Finally Miller's Principle is derivable if both opinion and chance derive from a single subjective probability. 21 But that would make chance itself subjective, which is also not a feasible option. Yet as long as chance is postulated as a feature of the universe, which is not identifiable in terms of what happens, the fundamental question cannot be circumvented, dismissed, or finessed.
We will however return to this question later, with a different approach.
7. Possible Worlds and Explanation
Laws of nature are whataccording to the sympatheticscience aims to discover. If laws are what Pargetter, McCall, or Vallentyne says they are, is that contention plausible? Is the character of relations among possible worlds, or of functions on sets of worlds, what science aims to discover?
The answer, made perhaps most clearly by Pargetter, has two parts. The first part is that science aims to discover what is possible and impossible, probable and improbable. The second part is that what is possible and probable depends entirely on what is the case in this and related other possible worlds. Then it follows indeed that science aims to discover what not only our, but also those other related worlds are like. The plausibility of this two-part answer is certainly improved if we say not possible worlds but possible futures open to us now (or in the past).
Plausibility diminishes, however, when we gather that the possible worlds have no interaction or influence on each other, and that the other possible futures that we might have had will make no
end p.86
difference at all to what will actually happen. If it is true that wood burns in all possible worlds, then it is true that wood burns here, because our actual world is possible. But why is that reflection called explanatory? 22 If I ask why this animal is aggressive, and you tell me because all wolves are, and this is a wolf, I may be satisfied. But my satisfaction surely derives in this case from my background opinion which now adds to this that aggression, if prevalent in wolves, has a common cause, either because it is an inherited trait in mammals or because it tends to be induced by learning in the pack. No such back-up is available in the actual because true in all possible case. What if I had said This animal is aggressive because it is a wolf and all wolves are aggressive, although this is known not to be an inherited trait in mammals, nor ever induced by learning? You would surely complain that I had raised a much greater mystery than you had already?
This objection must seem strong to anyone who takes causal accounts as needed for explanation. I do not have such stringent criteria. 23 But I do think that to be an explanation, the proffered information must provide the missing piece in the puzzle that preoccupies the questioner. This presupposes that he has already pieces in place, which the newly offered piece fits into. By my weaker criteria, the above reflection remains an objection, unless we can construct a question to which It is so in all accessible possible worlds is a relevant and informative answer.
McCall and Vallentyne appear to be sensitive to this issue and their talk of the nomic structure of the world may be an attempt to speak to it. Suppose all wood burns not only now, and always in the past, but also in every possible future. Is that not a good meaning for the assertion that it is causally necessary for wood to burn? Is it not intuitively plausible to think that what happens in all possible futures, reveals causal relations and causal necessity?
Yes, to the extent that these terms are clear, that is indeed plausible. But surely the plausibility derives from the fact that all our possible futures are rooted in our settled past, and the past determines important features of the future to come? In other worlds, It is so in all possible futures points to a causal explanation, which it does not itself provide. McCall and Vallentyne take away this very basis of the plausibility, it seems to me, if they deny that the possible futures common character is there because of what the past is like. And that is what they do, if they explicate the past
end p.87
truth of modal statements, as amounting simply to the common character of the futures.
But perhaps objective chance is something that resides in the past, in addition to what actually happened? And it is due to this past objective chance that the futures are the way they are? Then it is not the way the alternative possible futures are, even considered collectively as a family, which accounts for the regularities in actual world historyit is rather that objective chance from which they too derive their character. In that case we need to be told what this objective chance is, and how it influences the events to come. The answer given, however, is that to say what the chance is, consists in delineating the proportions of possible futures in which various events come about. So we are led full circle, again, with the second part of the answer taking away the plausibility accrued to the first.
8. Relation to Science: Pandora's Box
Whether possible-world models are truly explanatory has now been put in doubt. But suppose we agreed that they are. What riches and resources would this not open up for scientific explanation, in a new and higher key? I recall a news item in the Fortean Times a few years ago, of a physicist, intrigued with the many-worlds interpretation, who speculated that worlds might interact after all. Specifically, he reflected, this could explain why psychics tend to be wrong so often in their predictions (they see into another possible world and their predictions are right about that world). But I think we need not go so far as to postulate interaction. It is a common view that entities and individuals existing in this world also exist in some others (and that we will continue to exist into most of our possible futures). 25 That is enough, I think, to create new and interesting sorts of explanations in physics, if we take it seriously. 26
Imagine a world which is not entirely deterministic.
Specifically, there is a type of crystal, let us call it the Q-crystal,
which begins to glow in vacuo at temperature 100C, with probability ![]() .
There are no conditions besides atmospheric pressure and temperature which have
any effect at all relevant to this phenomenon. Yet some of these crystals
always do so, some never, and some in apparently
.
There are no conditions besides atmospheric pressure and temperature which have
any effect at all relevant to this phenomenon. Yet some of these crystals
always do so, some never, and some in apparently
end p.88
random fashion half the time. Let us add that these three
types of behaviour appear among naturally occurring Q-crystals in
proportions ![]() .
Thus if a randomly selected natural Q-crystal is subjected to the test,
it has a probability
.
Thus if a randomly selected natural Q-crystal is subjected to the test,
it has a probability ![]() of
glowing. It is important that the three types of behaviour form a
classification only applicable in retrospect and not predictable on the basis
of any independent detectable characteristic. 27
of
glowing. It is important that the three types of behaviour form a
classification only applicable in retrospect and not predictable on the basis
of any independent detectable characteristic. 27
The example is meant to be schematic, and is about crystals and glowing only to aid our visual imagination. The important point is that the scientists in the imagined world regard this account as ultimate, with its probabilities irreducible.
In popular science articles, the writers there make such profound observations as that it is as if the crystals remember their past history. If they have glowed every time so far, they are more likely than not to glow again next time. But if they have ever glowed and also sometimes failed to glow under those conditions, they are exactly as if they flip a perfectly fair coin each time to determine their behaviour. All this despite the complete absence, according to the physicists there, of any mechanism or structure that could act like a memory bank. You may now have read some actual popular book or article about elementary particles in quantum mechanics, elaborated with references to telepathy, time-travel, Oriental mysticism, and the likethe imagined world is sure to have its counterpart in its bookstores.
But modal realism now opens the door for a truly explanatory
account, going beyond what the reputable scientists have said so far. You see,
this imagined world is physically possible relative to other worlds. Call our
central imagined world W. It is physically possible relative to the
completely deterministic W+, in which each Q crystal must
glow under those conditions of pressure and temperature. World W is also
physically possible relative to deterministic world W−, where each
Q crystal must fail to glow under those conditions. If now a Q
crystal in our world W exhibits the first (always glowing) behaviour
pattern, that is because it is a crystal which also exists in W+.
And if it never glows, that is because it is also one of the crystals of world W−.
The explanation is powerful, simple, and explains something which has no other sort of explanationand which is just too regular to be plausible as a coincidence. Shall we not recommend
end p.89
this pattern of explanation to science? Indeed, in our very own world, in this century, physicists must deal conceptually with patterns of apparent pre-established harmony in indeterministic phenomena. Should they not be made to realize the extraordinary explanatory power of hypotheses about worlds from which there is access to ours? Is this the great gift analytic philosophy can finally bring to science?
9. The Perils of a Reified Model
There is good to be found in, or behind, the possible-worlds story, and our critique should not end without some attempt to uncover it.
Under what conditions is it true, or false, to say that it is a law of nature that, for example, momentum is conserved in collisions? There are three possibilities. The first is that there is such a law (in our world), the second is that this law is violatedagain, in this worldbecause in some collision the total momentum is not the same before and after. But if that were all, if actual violation was the only way the law claim could be false, then law would be mere regularity. That is not in accordance with the concept of a law of nature, so we must add the third possibility: the law is never violated in actuality, yet it is not a law of our actual world. The very idea that laws are more than mere regularities entails that a law claim could be false, although nature harbours no actual counterexample.
In the extreme, this reflection becomes: this world could proceed, in all its occurrences and throughout its history, in just the way it does although it has no laws at all. Pargetter calls a world without laws a Hume world. In the possible-worlds jargon this is equivalent to: a world relative to which all worlds are physically possible.
Imagine I have a trans-world travel machine, and take you on a tour. I can program it to take us to another world, provided our world bears Pargetter's access relation to it. I can also program it so as to take us to a world which has, or lacks, specific laws which I type into the console. To begin I type: delete all laws. I press the Entry button, and as far as you can see, there is no change in our situation at all. Don't be afraid, I say. We are now in a Hume world, but it is one which has exactly the same world-history, past and future, as ours. We quickly gather some experimental evidence for this claimfor example, I release a pencil and lo! it does fall to the floor. From a Hume world, we can go to any world at all, so I choose one where pigs fly. I press Entry, and we see a pig happily flying by outside. That is the only lawlike fact about this world, I say, but happily it is very much like the Hume world we just came from, and you are not likely to have other surprises. Just then you catch a glimpse of a white rabbit hurrying by with a pocket-watch, but I press Entry again and tell you we are arriving safely back in that Hume world. Now, after all these adventures, don't you wish I'd quickly get us back to our own safe home? I can do it, of course; but tell me, is there any reason for us to return?
That Hume world is just like ours, all the same things happen in it, but it has no laws. My world-travel machine has actually introduced one experimentally verifiable difference: from that Hume world it can take us in one step to where pigs fly, but from our original world it needs two steps. Unfortunately for the story, this machine is a fiction; it not only does not but cannot exist.
So, there is no occurrent difference between the two worlds at all. There is no observational or experimental evidence anyone could gather, that would have any bearing on whether we are in that Hume world, or in our supposed original. Equivalently: no such evidence could bear at all on the question whether we don't really live in a Hume world already.
This makes the possible-world story a fancy tale indeed. Its friends add the coda: but that there are laws which make the actual regularities necessary is the best explanation of why these regularities should be there at all. Hence we should believe that we are not in a Hume world, but in one with laws. No experimentum crucis is possible, that is true; but the conclusion that there are laws is deduced by inference to the best explanation.
We will have another chapter to discuss this point of epistemology. Now I want to present a different view: the idea, that science describes what is possible (and necessary, probable, and improbable), is correct but means something quite different. According to my view, this story of possible worlds reifies a modelthat is, it attributes reality to what is only a means of representation.
In a discussion of science, possibility and necessity enter in two ways. Taking the point of view of an accepted theory, speaking ex cathedra so to say, we declare impossible whatever this theory
end p.91
denies. That is what we do if we say flat out that no perpetual-motion machine can exist, or that no body can be accelerated to the speed of light. Secondly, still in this same way, we may declare something possible if the theory allows it, under certain conditions, and we have no information to the contrary. This is the possibility of ignorance, sub specie the belief involved in theory acceptance. For our assertion signals that the facts in question are accommodated in some model our theory provides, and we have no evidence at odds with that model.
In addition, inside the theory's models, we may find alternative possibilities as well. This can happen only if the theory is not deterministic. For example: in its models, certain events happen with some probability, and other contrary events happen with some positive probability too. In that case, if someone who accepts the theory says that either type of event may happen, he is not merely signalling ignorance. For he admits that with only the belief involved in accepting this theory, plus maximal information about relevant conditions, he would still admit these alternatives as possible.
So far, our ontological baggage includes only persons, theories, models, and actual events. To say that of two events only one can occur actually, but both are possible, does not imply that both are real. The possible worlds accounts we have now inspected add that both are real. For they entail that on the correct understanding of possible this is so.
We can see the main motive for this idea in our brief, intuitive discussion of how possibility talk arises. For the person speaking sub specie acceptance of a theory clearly believes that the way the world is, is correctly represented by some model of the theory. Now what is this correctly represented? If we take it to mean not only that what is real is represented in the model, but also that every element of the model represents some part or aspect of reality, then we are at home with the realists. For then, if the model contains alternative possible courses of events, it follows that mutually incompatible events are all real. The more grandiloquent possible world is not essentially less innocuous than possible event.
This characterization of the relation of a good model to reality reifies the model. It equates model and reality, in effect. And suddenly, the goodness of good models goes way beyond any relation to what we can verify, even in principle, for it must include
end p.92
correctness about what did and also about what does not happen in actuality. No great esteem for the notion of verification is needed to see the problems this raises. Make your requirements of verifiability or testability as weak, as modest as you like, and they will still never allow you to say: we have checked that this model is correct about what did not happen, about the experiment we did not carry out, as well as about what did happen. There is undoubtedly more to be said about the relations of models to phenomena. Especially, the question of how we can become rationally confident that a model does fit the phenomenawhich after all stretch beyond our ken in space and timewill need to be taken up. But with that postponed for now, the reification of alternative possibilities has not proved fruitful for us. It required the introduction of relations and functions defined on possible worlds, which (a) could not be identified, (b) did not appear to warrant prediction or rational expectation, (c) seemed not to explain, (d) gave authority to pseudo-science, and (e)c'est le bouquetbrought us into an excess of metaphysics. However plausibly the story begins, the golden road to philosophy which possible-world ontologies promise, leads nowhere.
end p.93
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1476
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved