| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
UNIVERSITÉ POLYTECHIQUE BUCAREST
FACULTÉ DE GÉNIE EN LANGUES ÉTRENGÈRES
RECHERCHE SCIENTIFIQUE
PREMIER SEMESTRE
UN OUTIL UTILE:
LA PROGRAMMATION LINÉ
UN OUTIL UTILE:
LA PROGRAMMATION LINÉ
1. DÉFINITION GÉNÉRALE
La programmation linéaire est la recherche extremum (maximum ou minimum) d’un fonction linéaire de n variables liées par un systÈme de m relations linéaires (équations ou inéquations) appelées contraintes.
Soit, avec les notatioms généralement usitées:
F=![]() i
= 1 à n
i
= 1 à n
la fonction
et ![]() j
= 1 à m
j
= 1 à m
les contraines.
On peut associer à l’ensemble des variables xi un espace vectoriel à n dimensions qui contient en particulier les vecteurs solutions X.
Un certain nombre de problémes industriels de nature technico-économique relevant de la programmation linéaire.
C’est le cas, en particulier, chaque fois que l’on cherche à optimiser une fonction économique dont la dépendance vis-à-vis des variables inconnues du problÈme est de forme linéaire et que, par ailleurs, les mÊmes variables sont liées par des contraintes linéaires traduisant en general des limites de capacité.
Ainsi, dans une entreprise fabriquant plusieurs produits, la marge brute totale pour une période d’exploitation donnée est, dans certaines limites, une function linéaire des quantités fabriquées et vendues de ces différents produits.
Tandis que ces mÊmes quantités sont liées par des relations linéaires traduisant les limites de capacités de production (ou de ventes) de l’entreprise.
La programmation linéaire se rattache au probléme beaucoup plus général de la recherche d’extrema liés qui avait reçu une solution générale dÈs le XVIIIe siÈcle.
En effet, on sait qu’étant donné une function de n variables
f(x1, x2, ……….., xn) = 0
liées par m relations
f1 (x1……………xn) = 0 fm (x1………..xn) = 0
pour trouver les extrema de f on adjoint aux m relations ci dessus les equations obtenues en égalant à zero les derives partielles de la function f + λ1f1+…..λmfm
Les coefficients λ sont les multiplicateurs de LAGRANGE.
En principe, on disposait donc d’une méthode tout à fait générale et débordant d’ailleurs le cas particulier de la programmation linéaire pour résoudre cette classe de problÈmes. En fait, la méthode des multiplicateurs de LAGRANGE s’est révélée peu practicable. C’est pourquoi des recherches ont été conduites aprÈs la seconde guerre mondiale.
Ces recherche ont abouti au développement d’une méthode entiÈrement originale, proper à donner la solution du problÈme general de la programmation linéaire. Cette méthode est connue sous le nom de MÉTHODE du SIMPLEXE ou de DANTZIG.
D’autres méthodes ont été proposées mais la méthode de Dantzig demeure, de trÈs loin, la plus utilisée du fait, certainement, de son efficacité.
Formulation mathématique standard du problÈme.
Bien que la formulation mathématique donnée ci-dessus soit déjà trÈs simple, une formulation « standard » a été proposée afin d’unifier la méthode et de ramener tous les cas de resolution à un modÈle unique. (Certains auteurs réser vent l’appellation de « canonique » à cette forme, d’autres l’appellent « standard »).
ASXS = d XS ≥ 0
minimiser f= CS XS
Les notations prenant les significations suivantes:
AS il s’agit de la matrice des coefficients des équations ou inéquations de contraintes
XS c’est le vecteur colonne à n composantes
X1.Xn
d vecteur colonne du second membre à m composantes
CS est le vecteur ligne de la fonction àmaximiser
On peut ramener toutes les formulations de problÈmes à cette forme standard dans la mesure oÙ:
Seules les valeurs positives des variables constituent des solutions possibles.
Les inéquations peuvent Être ramenées à des equations par l’introductin de variables supplémentaires, dites variables d’écarts.
Un changement de signe sur la function linéaire à optimizer peut toujours nous ramener au cas de la recherché d’un maximum (ou d’un minimum).
2. L’INTERPRÉTATION GÉOMÉTRIQUE
Le problÈme de la programmation linéaire reçoit une interprétation géométrique simple. En effet, les équations ou inéquations de contraintes linéaires représentent des droites, plans ou des hyperplans dans un espace à n dimensions ( n étant le nombre de variables). L’intersection de ces droites, plans, hyperplans définit un polygone, polyÈdre, hyperpolyÈdre, à l’intérieur duquel le systÈme des contraintes du problÈme se trouve satisfait.
Il s’agit alors de trouver, dans le domaine ainsi délimité, le ou les points qui optimisent la fonction. Cette interprétation est particuliÈrement simple dans le cas de deux variables seulement.
Soit, par exemple, la fonction à maximiser:
f = 3x1 + 4x2
et le systÈme de contraintes:
x1 + 3x2 ![]() 24
24
x1 + 2x2 ![]() 17
17
5x1 + 3x2 ![]() 54
54
x1 + x2 ![]() 0
0
Chacune des contraintes est représentée par une
droite du plan x![]() x
x![]() qui partage le plan en deux régions: une
régions oÙ la contrainte est satisfaite une région oÙ la
contrainte n’est pas satisfaite ( la droite étant elle-mÊme le lieu des
points pour lesqueles les conditions
d’égalité des deux mambres est satisfaite).
qui partage le plan en deux régions: une
régions oÙ la contrainte est satisfaite une région oÙ la
contrainte n’est pas satisfaite ( la droite étant elle-mÊme le lieu des
points pour lesqueles les conditions
d’égalité des deux mambres est satisfaite).
L’ amsemble des droites représentant les contraintes délimite un polygone OABCD qui est le domaine à l’intérieur duquel doivent se trouver les valeurs de x1x2 pour que l’ensemble des contraintes soient satisfaites.
Nous devons chercher le ou les points de ce domaine qui maximise la fonction .
Z = 3x1 + 4x2
Pour cela, nous pouvons nous contenter de
remarquer que la function à optimiser est une fonction linéaire de x![]() x
x![]() ,
donc une droite dont tous les points ont la particularité de correspondre
à une mÊme valeur de Z, et cette valeur sera maxi pour la droite la plus éloignée de l’origine. Soit sur le sommet C du polygone qui représente donc la solution cherchée.
,
donc une droite dont tous les points ont la particularité de correspondre
à une mÊme valeur de Z, et cette valeur sera maxi pour la droite la plus éloignée de l’origine. Soit sur le sommet C du polygone qui représente donc la solution cherchée.
Ainsi, un problÈme de programmation linéaire à 2 variables x1x2 comportant un certain nombre d’inéquations de contraintes donne lieu à l’ interprétation géométrique suivante:
Dans le plan des variables x1x2 le domaine des points qui satisfont au systÈme d’inéquations de contraintes est limité par un polygone à l’intérieur duquel devront se trouver les solutions. La fonction économique est également représentée par une droite comportant un paramÈtre qui est précisément la valeur de la fonction à optimiser.
f = C1x1 + C x2
de telle sorte que les points de la représentent l’ensamble des points du plan d’égale valeur économique (droite isoéconomique).
La droite isoéconomique de valeur nulle passe par l’origine.
Loersque Z prend des valeurs positives, la droite isoéconomique de valeur Z s’éloigne de l’ origine tout en restant parallÈle à la droite isoéconomique de valeur nulle.
La valeur du paramÈtre Z croit précisément comme la distance de la droite à l’origine.
La solution du problÈme se trouvera donc sur la droite parallÈle à la droite isoéconomique de valeur nulle et ayant au moins un points dans le polygone des contraintes.
Cette droite est, en général, une parallÈle à la droite isoéconomique de valeur nulle passant par l’un des somments du polygone.
Autrement dit, la solution se trouve en général Être l’un sommets du poly gone des contraintes.
On peut généraliser au cas de n variables:
- les droites deviennent des plans (n = 3) ou des hyperplans (n > 3)
- les polygones deviennent polyÈdres ou hyperpolyÈdres et la recherche de la solution consiste à chercher sur quel sommet du polyÈdre la fonction économique atteint son extremum.
Naturellement, le cas purra se présenter oÙ la droite isoéconomique sera paralléle à l’un des côtés du polygone des contraintes.
Dans ce cas, malgrétout exceptionnel, on aura, non pas un points comme solution, mais l’ensemble des points correspondants ai côté du polygone.
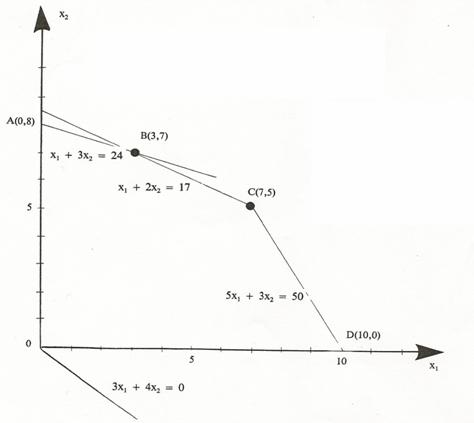
Figure. Résolution graphique d’un problem de programmation linéaire
3. EXEMPLE EN GESTION DE PRODUCTION
Soit une enterprise
fabriquant un certain nombre de prodits P1,P2,P3![]()
![]() ,…….Pn.
,…….Pn.
Pour ces
fabrications l’enteprise utilize un certain nombre de moyens (machines, postes
de travail manuel) M1, M2, M3, ……….., Mm et de telle façon que plusieurs de ces moyens
soient communs à plisieurs des produits![]() .
.
Les moyens M1, M2, ……., Mm ont des capacités limitées ; par exemple, on dispose chaque mois de tant d’heures de M1, de tant d’heures de M2.
Soient C1, C2. .Cm les limites de capacité des moyens.
D’autre part, sont connues les marges dégagées par chacun des produits fabriqués P1, P2, …….
Le problÈme qui se pose à toute entreprise travaillant suivant ce schéma est alors le suivant:
Quel est le programme de production ( quantité produite par mois des différents produits: soit x1 pour P1, x2 pour P2) qui maximise la marge total?
La méthode de programmation linéaire autorise l’introduction d’autres types de contraintes, par exemple commerciales.
Supposons en effet que la capacité d’écoulement soit limitée, par exemple, à Vi pour le produit Pi
Il suffira d’introduire la contrainte supplémentaire
xi (production de
Pi) ![]() Vi
Vi
qui est encore une inéquation linéaire.
Pour traduire les limites de capacité des moyens, il sera nécessaire de connaitre le temps employé sur chacun des produits, autrement dit les « gammes » de fabrication.
Note techique
La méthode du Simplexe ou de Dantzig
ProblÈme de maximisation.
L’interprétation géométrique que nous avons rappelée ci-dessus, au paragraphe 2, va nous aider à comprendre la démarche de l’algorithme de Dantzig ou du Simplexe.
Ainsi que nous l’avons noté, la solution cherchée se trouve Être l’un des sommets de l’hyperpolyÈdre défini par le systÈme des contraintes.
Partant de cette remarque, la méthode va consister, par une série d’itérations successive, à cheminer de sommet en sommet en améliorant à chaque fois la valeur de la fonction économique jusqu’à l’obtention de l’optimum.
Naturellement , pour éviter trop de calculs, nous partirons d’un sommet aussi voisin que possible de la solution. Lorsqu’on ne connait pas un tel sommet, ce qui est souvent le cas, il sera toujours possible de partir de l’origine des coordonnées qui est elle aussi, rappelons-le, l’un des sommets de l’hyperpolyÈdre, le moins intéressant de tous, cependant, puisqu’à l’origine la fonction économique a une valeur nulle.
Tel est le principe de la méthode du Simplexe. Il reste à définir l’algorithme du calcul.
Nous commencerons par ramener le systÈme d’inéquationa linéaire à un systÈme ne comportant que comportant que des équations par l’introduction de variables d’écart.
m étant le nombre de contraintes, nous aurons à introduire au maximum m variables d’écart.
Ainsi, le systÈme pris en exemple au paragraphe 2 va s’écrire:
x1 + 3x2 + x3 = 24
x 1+ 2x2 + x4 = 17
5x1 +3x2 + x5 =50
x3, x4, x5 sont les variables d’écart qui nous ont permis de transformer le systÈme d’inéquations linéaires en un systéme linéaire d’équations.
De façon générale, le systÈme linéaire s’écrira sous forme matricielle:
AX = D
CX = f
X =
D =
C =
On appelle base B un ensemble de vecteurs colonnes aj linéairement indépendants.
Les m variables correspondantes sont les variables de base du systÈme; les (n - m) autres variables sont les variables secondaires ou hors-base.
Si B est une base et que l’on annule les variables hors base du systÈme, on obtient un systÈme de Cramer don’t la solution est connue.
Cette solution est la solution de base associée à B.
Le passage d’un sommet de l’hyperpolyÈdre à un autre sommet voisin dans l’espace à m dimensions se fera en échangeant un vecteur de la base B avec un autre vecteur hors base.
Nous savons faire ce changement de base et nous servirons des formules de transformation bien connues en algebra linéaire pour calculer la nouvelle matrice des coefficients.
La disposition pratique des calcul se fait sous la forme d’un tableau, dit « tableau du Simplexe » , qui reproduit la matrice des coefficients du systÈme linéaire à laquelle on adjoint une ligne et une colonne marginales.
La ligne marginale représente les coefficients de la forme linéaire de la fonction économique, tandis que la colonne indiquera les noms des variables de la base.
Ainsi, pour le systÈme linéaire que nous avons pris en exemple, le tableau de départ du Simplexe se présentera de la façon suivante:
|
X1 |
X2 |
X3 |
X4 |
X5 | ||
|
- f | ||||||
|
X3 | ||||||
|
X4 | ||||||
|
X5 |
Le tableau correspond au systÈme d’équations linéaire suivant:
x1 + 3x2![]() +
x3 = 24
+
x3 = 24
x1 + 2x2![]() + x4 = 17
+ x4 = 17
5x1 + 3x2 + x5 = 50
et à la forme linéaire suivante de la function économique:
f = 3x + 4x
x , x , x sont les variables d’écart.
Nous voyons qu’elles constituent également les variables de la solution de base puisque nous les avons fait figurer dans la colonne de gauche qui indique précisément , suivant nos conventions, les variables de base.
En effet, puisque nous n’avons aucune connaissance a priori des coordonnées des sommets du polygone des contraintes, nous partons de la solution triviale:
x1 x3
x2 x4
x5
qui correspond à l’origine des coordonnées.
La fonction économique correspondant àce point est évidemment nulle, ce que nous indiquons en faisant figurer la valeur 0 dans la case en haut et à droite du tableau.
Pour passer de l’origine à un autre sommet du polygone des contraintes, nous allons faire rentrer dans la base l’une des variables x1 ou x2 et, corrélativement, faire sortir l’une des variables d’écart x3, x4 ou x5, variable dont la contribution à la fonction économique est nulle.
Le choix de la variable d’entrée se fera d’aprÈs la valeur du coefficient des variables dans la fonction économique.
C’est l’objet du premier critÈre du Simplexe:
La variable d’entrédans la base est celle dont le coefficient dans la fonction économique est le plus élevé.
Dans l’exemple traité, ce sera donc la variable x2 qui va rentrer dans la nouvelle base.
Comment sélectionne – t – on la variable sortante?
Avant d’énoncer la rÈgle générale qui constitue le second critÈre du Simplexe, voyons comment se présente le problÈme dans notre exemple:
D’aprÈs ce qui vient d’Être dit, la nouvelle solution de base va comporter la variable x2 et deux des trois variables d’écart x3, x4, x5.
Nous aurons donc à satisfaire au systÈme suivant:
3x2 + x3 = 24
2x2 + x4 = 17
3x2 + x5 = 50
L’une des trois varibles x3, x4, x5 nulle sera variable sortante de la base.
Or, il est facile de voir sur cet exemple simple que la seule solution possible est x3 = 0 x2 = 8
En effet, les deux autres équation donnent pour x2 des valeurs supérieurs
![]() et
et ![]() >
> ![]() = 8
= 8
ce qui conduirait à un x3 < 0.
Cette considération se généralise dans le second critÈre du Simplexe:
La ligne qui va définir la variable sortante est celle pour laquelle le quotient des termes constants (les termes de la colonne de droite du tableau) par les coefficients de la variable entrante est le plus petit positif.
Dans l’exemple, c’est x3.
Ainsi , la nouvelle base est définie par les variables x2, x4, x5.
Nous cheminons donc depuis l’origine vers le sommet du polygone des contraintes situé sur x2.
La nouvelle solution sera définie par le deuxiÈme tableau du Somplexe, qui se déduira par application des formules de transformation de l’algÈbre linéaire, dont l’application particuliÈre à la programmation linéaire donne lieu à la « rÈgle du pivot ».
Revenons à notre premier tableau, nous avons vu ( 1er critÈre du Simplexe) que la variables entrante était x2, et ( 2e critÈre du Simplexe) que la variable sortante est x3.
Le coefficient qui se trouve au croisement de la colonne de la variable entrante x2 et de la ligne de la variable sortante x3 est le « pivot » . Il va servir à calculer tous les autres coefficients du deuxiÈme tableau du Simplexe.
Nous transformons le tableau initial de tell façon que la variable entrante apparaisse dans la premiÈre colonne à la place de la variable sortante. Les variables absentes de la premiÈre colonne ( donc variables hors-base) sont nulles.
Nous substituons donc, dans la premiÈre colonne, x2 à x3.
Les nouvelles valeurs des coefficients tirées des formules de changement de base peuvent se résumer de la façon suivante:
Soit aij le pivot (ligne i, colonne j),
Les nouveaux coefficients de la colonne du pivot ( colonne j) sont tous nuls, sauf le pivot qui est égal à 1.
Les nouveaux coefficients de la ligne du pivot (ligne i) sont égaux aux anciens divisés par la valeur du pivot.
Un autre terme quelconque, soit akl ( ne figurant ni sur la ligne, ni sur la collone du pivot) est égal à son ancienne valeur akl moins le produit des termes rectangles constants akj et ail divisés par le pivot.
Soit , suivant l’expression formelle:
a’kl
= akl - ![]()
si le pivot est aij
le nouveau terme a’kl
l’ancien akl.
Appliquons ces 3 rÈgles à l’exemple, nous abtenons le nouveau tableau suivant du Simplexe, correspondent à la premiÈre itération:
|
X1 |
X2 |
X3 |
X4 |
X5 | ||
|
- f | ||||||
|
X2 | ||||||
|
X4 | ||||||
|
X5 |
Chaque terme de ce second tableau a été calculé en appliquant les trois rÈgles rappelées ci-dessus.
Quelle est l’interprétation de ce second tableau du Simplexe?
Il correspond au passage de la solution de base origine des coordonnées à la solution de base correspondant au sommet du polygone situé sur l’axe x2 pour lequel nous lisons dans le tableau:
x1 = 0 (variable hors-base)
x2 = 8
x4 = 1 (premiÈre variable d’écart)
x5 = 26 (deuxiÈme variable d’écart)
Ce point correspond au sommet A de la solution géométrique.
Le tableau nous donne en outré la nouvelle valeur,changée de signe, de la fonction économique, soit f = 32.
Tout ceci est aisément verifiable.
Nous venons d’effectuer un pas du calcul du Simplexe correspondent à la premiÈre itération. Pour l’itération suivante, on procÈdera de mÊme.
Cette fois-ci, la variable entrante sera la variable x1 (premier critÈre du Simplexe: plus fort coefficient de la fonction économique) et la variable sortante x4 car la division des termes constants (8, 1, 26) respectivement par les coefficients de la colonne x1(1/3, 1/3, 4) donne le coefficient de x4 comme celui de la valeur la plus faible (deuxiÈme critÈre du Simplexe).
Le pivot est donc 1/3 (croisement de la colonne x1 avec la ligne x4).
D’oÙ le nouveau tableau du Simplexe correspondant à la deuxiÈme itération:
|
X1 |
X2 |
X3 |
X4 |
X5 | ||
|
- f | ||||||
|
X2 |
| |||||
|
X1 | ||||||
|
X5 |
Qui correspond à la nouvelle solution de base:
x1 = 3
x2 = 7
x3 = 0 variable hors base
x4 = 0 variable hors base
x5 = 14 variable d’écart
f = 37
Ce point correspond au sommet B de la solution géométrique.
Une nouvelle iteration est possible tant que l’un des coefficients de la function économique a une valeur positive. C’est le cas ici.
Une nouvelle application de l’algorithme conduit au nouveau tableau:
|
X1 |
X2 |
X3 |
X4 |
X5 | ||
|
- f | ||||||
|
X2 | ||||||
|
X1 | ||||||
|
X3 |
qui correspond à la solution de base:
x1 = 7
x2 = 5
x3 = 2 variable d’écart
x4 = 0 variable hors base
x5 = 0 variable hors base
Ce point correspond au point C de la solution géométrique, c’est-à-dire à l’optimum cherché.
Nous constatons qu’aucun coefficient C n’est plus positif, le calcul est donc bien terminé.
La valeur de la function économique est f = 41 correspondant au maximum.
Par exemple, avec trois machines et trois moyens, nous aurons le tableau suivant:
|
M1 M2 M3 |
|
P1 t11 t12 t13 |
|
P2 t21 t22 t23 |
|
P3 t31 t32 t33 |
|
Capacités C1 C2 C3 |
Alors , les limitations de capacités se traduiront par le systÈme d’inéquations:
x1t11 + x2t21 + x3t31 ≤ C1
x1t12 + x2t22 + x3t32 ≤ C2
x1t13 + x2t23 + x3t33 ≤ C3
D’autre part, si la marge degage par P1 este m1, P2m2, P3m3: la marge totale pour le programme x1 x2 x3 est
M = x1 m1 + x2 m2 + x3 m3
que nous devons maximiser.
Il s’agit bien là d’un problÈme de programmation linéaire qui relÈve donc de la Méthode du Simplexe.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 826
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved