| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
UNIVERSITÉ POLYTECHNIQUE BUCAREST
FACULTÉ DE GÉNIE EN LANGUAES ÉTRANGÈRES
RECHERCHE SCIENTIFIQUE
DEUXIÈME SEMESTRE
LA PRÉVISION
ET LA GESTION DES STOCKS
LA PRÉVISION
ET LA GESTION DES STOCKS
1. LA PRÉVISION DES VENTES ET DES CONSOMMATIONS
Ainsi que nous l’avons dit au début de ce chapitre, la gestion rationnelle de la production nécessite l’emploi de méthodes de prevision adaptées à la fois aux types de marché couverts par l’entreprise at aux types de fabrication qu’elle a choisis.
L’existence des moyens informatiques a permis de réaliser des progrÈs importants dans les méthodes de prévision: les simulations ont conduit à mettre au point des modÈles se rapprochant assez exactement de l’évolution réelle des ventes.
Les methods employees sont différents suivant qu’il s’agit de prevision à long terme ou de prevision à court terme.
1.1. PRÉVISION A LONG TERME
Le marché peut Être l’objet de modification profondes, telles que la hausse des matiÈres et produits pétroliers à partir de l’automne 1973. Néanmoins, une analyse poussée des différents facteurs intervenant sur le marché étudié peut permettre d’obtenir des résultats intéressants indispensables à toute enterprise qui realize des investissements productifs importants – à échéance de 2 ou 3 ans. On a pu noter dans l’évolution à long terme des marches l’existence de phénimÈnes de rattrapage tells que, sur plusieurs années, un modÈle bien étudié se rapproche d’assez prÈs de la réalité.
Par exemple, une etude de l’I.N.S.E.E., parue en 1971, sur la prévision des immatriculations de véhicules de tourisme neufs por 1975, donnait le chiffre de 17500000 véhicules; le chiffre réel, en raison de la crise pétriliÈre, n’a été que de 1480000; mais, en 1976, ce chiffre était de 18750000: un événement aussi considerable que la crise de 1973 a donc entrainé une perturbation proviso ire, puis un rattrapage.
De telles etudes sont menées suivant une méthode rigoureuse, integrant un certain nombre de critÈres essentiels, choisis aprÈs analyse.
Pour l’étude en question les critÈres suivants ont fait l’object de choix de modÈles et de simulation:
- Évolution du nombre de ménages, donnée de base la plus sÛre car relevant directement de la démographie.
- Évolution du Produit National Brut et, corrélativement, du Revenu par ménage.
- Évolution du taux de possession en function du revenue, à la fois le premier véhicule et pour le deuxiÈme véhicule.
- Évolution du coÛt des véhicules, qui peut modifier le taux de possession.
Les taux obtenus sont ensuite corrigés pour tenir compte de certains phénomÈnes, tells que la croissance des grandes agglomérations, le vieillissement de l’age moyen des chefs de ménage qui, tous deux, diminuent le taux de possession.
La combinaison de ces différents critÈres donnera finalement la croissance du parc automabile sur les 5 années considérées.
Un deuxiÈme element fundamental concerne le nombre annuel de véhicules neufs remplaçant des véhicules hors d’usage. Ce nombre représente à peu prÈs 60 à 65 % du total des immatriculations. Il dépend de la durée de vie moyenne des véhicules, actuellement de l’ordre de 11 ans.
Mais cette durée peut, suivant l’évolution de la conjoncture économique et de la politique des fournisseurs, soit diminuer, soit rester étale , soit augmenter. Il convient alors de faire différentes hypothÈses qui donneront plusieurs chiffres prévisionnels.
Beaucoup d’études poussées de marché intÈgrent un trÈs grand nombre de facteurs et combinent plusieurs hypotheses. En procédant à une sectorisation rationnelle, on arrive à améliorer la prevision. Les factures qui interviennent sont le plus souvent:
Les factures démographiques: age moyen, nombre d’enfants, tranches d’age,….
Les factures géographiques: zones urbaines, zones rurales, latitude, climat,….
Les facteurs socio – économiques: catégories professionnelles, revenus, tendance politique, religieuse,.
Il est fréquent de voir prendre en compte, pour des simulations, plus de 100 facteurs différents.
1.2. PRÉVISION A COURT TERME
Elle est liée à l’évolution du marché et à la vie du produit. Sa période de validité est donc limitée par la stabilité des facteurs de base pris en compte.
En fait, à court terme, les aléas on tune importance considerable. Des phénomÈnes comme l’inflation, la fiscalité, l’anticipation sur l’augmentation des prix de matiÈre, amÈnent des variations imprévues qui remittent en cause des previsions couvent bien étudiées.
Aussi faut-il combiner le maximum de sources d’information.
Parmi celles – ci on distingue deux catégories principales:
1.2.1. Les sources internes
- Relevés statistiques: commandes, ventes, clients nouveaux, clients perdus.
- Les informations du réseau de distribution.
- Les informations provenant des contacts directs avec les utilisateurs: par le canal des représentants, service aprÈs-vente, technico-commerciaux.
1.2.2. Les sources externes
- Organismes syndicaux professionnels.
- Chambres de commerce.
- Renseignements directs sur la concurrence.
- Statistiques de l’I.N.S.E.E.
- Les ministÈres (Budget).
- Le commissariat au plan.
- Les documents douaniers.
- Les cabinets specializes dans les enquÊtes de marché et panels.
La prévision à court terme doit permettre de déterminer trois éléments principaux:
- La tendance, c’est-à-dire l’évolution prévue des ventes, en général, d’une année sur l’autre: % d’augmentation, de diminution ou stagnation, la tendance peut également Être indiquée en chiffres bruts.
- L’existence de variations saisonniÈres, sensibles dans la majorité des industries.
- L’intervention d’aléas et les limites de leur étendue.
Ces différents éléments peuvent Être calculés à partir des statistiques existantes, c’est-à-dire qu’on procÈde par extrapolation des courbes de ventes dans le temps.
Mais il convient d’employer d’autres méthodes permettant des comparaisons.
Pour le calcul de la tendance, on procÈdera à des analyses de co-variation; c’est-à-dire qu’on examinera les variations semblables de deux produits avec calculs de corrélation: par exemple, emballages pour les produits de grande consommation.
On peut également effectuer des sondages des ventes sur un échantillon de population; on obtiendra les intentions d’achats dans les mois à venir: méthode efficace mais coÛteuse.
Une bonne précision néce ssite l’emploi de plusieurs méthodes et une analyse poussée des résultats obtenus par chacune de ces méthodes.
1.2.3. Utilisation des séries chronologiques
C’est évidemment la méthode la plus rapide et la moins coÛteuse pour peu que les statistiques soient bien tenues.
Le tableau ci-dessous donne, pendant 4 années consécutives, les relevés de ventes par une entreprise fabriquant des raccords hydrauliques.
|
A - 4 |
A - 3 |
A - 2 |
A - 1 |
Total |
Coefficient |
en% |
|
|
Janvier. | |||||||
|
Février. | |||||||
|
Mars.. | |||||||
|
Avril. | |||||||
|
Mai | |||||||
|
Juin | |||||||
|
Juillet | |||||||
|
AoÛt.. | |||||||
|
Septembre.. | |||||||
|
Octobre | |||||||
|
Novembre.. | |||||||
|
Décembre.. | |||||||
|
Total. | |||||||
|
Moyenne m. | |||||||
Un tel historique montre les modifications de la tendance, en accroissement respectivement:
de 16 % entre A – 3 et A – 4
de 18,5 % entre A – 2 et A – 3
de 14,7 % entre A – 1 et A – 2
La prévision de tendance résultant de l’historique serait donc de l’ordre de 16 % si l’analyse de la situation et les autres sources d’information ne conduisaient pas à modifier ce chiffre.
Le montant total prévisionnel des ventes, l’année A, pourrait donc Être de 592 000.
Pour une bonne connaissance de la tendance, il est nécessaire de désaisonnaliser les séries statistiques, comme le font couramment les services publics. A cet effet on calcule les coefficients saisonniers, comme nous l’indiquons en note technique.
1.2.4. Ajustement par lissage exponential
Cette méthode consiste à corriger la prevision des écarts entre le réel et le prévisionnel.
Pm étant la prévision pour le mois m, Vm la vente réelle (ou la consommation) on a:
Pm = Pm-1 + ![]() (Vm-1 – Pm-1)
(Vm-1 – Pm-1)
ou
Pm
= ![]() Vm-1
+ (1-
Vm-1
+ (1-![]() )Pm-1
)Pm-1
Le coefficent ![]() peut varier de 0,1 à 0,5. Il est déterminé par l’expérience.
peut varier de 0,1 à 0,5. Il est déterminé par l’expérience.
Plus ![]() est grand, plus on donne d’importance au
dernier résultat.
est grand, plus on donne d’importance au
dernier résultat.
En effectuant le calcul on a:
Pm = αVm-1 + α(1 - α) Vm-2 + α(1 - α)2Vm-3 + .. + α(1-α)m-2V1 + (1-α)m-1P1
Pour α = 0.25 par exemple:
P13 = 0.25V12 + 0.187V11 + 0.141V10 + 0.105V9 + 0.079V8 + 0.059V7 + 0.044V6 + 0.033V5 + 0.025V4 + 0.018V3 + 0.014V2 + 0.01V1 + 0.031P1.
On aura immédiatement P14 = 0.25V13 + 0.75P13
Des formules plus simples ne prennent en compte que les sept derniers mois.
2. LA GESTION DES STOCKS
2.1. NATURE DES STOCKS – L’EFFORT DE RÉDUCTION
Le caractÈre saisonnier des nombreuses demandes de biens de consummation et celui de beaucoup de sources d’approvisionnement a de tout temps entrainé la nécssité de constituer des réserves. Stock, mot saxon, signifie bÛche ou souche, et rappelle le nécessité de constituer des provisions de bois pour l’hiver. Cette notion de saisonnalité s’est étendue plus généralement au besoin de régulariser la production face à une demande variable et, parallÈlement, de satisfaire une demande réguliÈres en matiÈres et piÈces face à un approvisionnement discontinu et soumis à différents aléas de délais.
On constitue également des stocks pour des raions économiques, telles que: quantités minimas vendues ou lancées, contraintes de magasinage, de transport, de livraison, rabais suivant les quantités, et enfin pour des raisons dues à l’évolution spéculative des prix de la monnaie.
On distingue:
Les stocks de prodits finis, ensembles pour les montages, rechanges, accessoires, ingredients, emballages, livrables à la clientele.
Les stocks nécessaire à la fabrication: matiÈres premiÈres, ébauches, pieces spéciales sous-traitées, pieces normalisées, pieces intermediaries fabriquées dans l’entreprise.
Les pieces de recharge pour le parc machines, les outillages spéciaux, les outillages et matiÈres consommables, les pieces, matériaux, prodit pour l’entretien des batiments et installations de fluids (électricité, air comprimé, vapeur, chauffage).
Les en-cours qui seront traits à part.
Les stocks constituent à la fois une nécessité et une lourde contrainte financiÈre. Il suffit de dire que montant des stocks de matiÈres premiÈres dans les enterprises correspond à 30 % du total de leur capital.
A l’échelon national, le montant total des stocks de toutes natures représente plus de 20 % du P.I.B.
Le coÛt annuel des stocks représente en moyenne 25 % des capitaux immobilisés.
Il faut donc obtenir des stocks minimum permettant d’assurer la sécurité des approvisionnements et la régularité des livraisons à la clientÈle. Les Japonais ont introduit la notion de << stock 0>> reprise par de nombreuses entreprises occidentales. Elle symbolise un effort constant de réduction, possible dans beaucoup de branches industrielles mais qui requiert de tous une attention sans relache pour éviter les ruptures et les arrest de fabrication.
La gestion comprend un certain nombre d’actions quasi automatiques:
le magasinage: entrées, ctockage, sorties des articles;
la tenue du fichier suivant une périodicité à définir;
l’imputation dans la comptabilité des entrées et sorties.
Elle comprend un choix dans la définition d’un certain nombre de critÈres:
le classement du stocks en categories, le plus souvent établi d’aprÈs la méthode ABC.
Ce classement résulte du fait que les articles d’un stocks obéissent à une loi de distribution, appelée Loi de GALTON, c’est-à-dire une distribution gausso-logarithmique.
Il en résulte que, si l’on classe les articles en ordonnée, en prenant par exemple le critÈre: % valeur de consummation annuelle, pris en ordre décroissant, et qu’on place en abscisse le pourcentage des rangs des articles, on obtient une courbe qui conduit en premiÈre analyse à classer les articles en trios categories. En general, dans les industries de construction mécanique:
Catégorie A: 10 % des articles représentent 75 % à 80 % de la valeur du stock.
Catégorie B: 25 % des articles représentent 15 % à 20 % de cette valeur.
Catégorie C: 65 % des articles représentent moins de 5 % de cette valeur.
Une analyse plus poussée montre
qu’il existe entre les articles classés à des rangs situés au plus
prÈs des pourcentages correspondant aux écarts-types de la Loi de GAUSS en cumulé, un rapport constant ![]() ,
variant de 2 ou 3 à 25, caractérisant la technicité de l’entreprise. Plus
la technique est élaborée, plus la valeur des articles est étalée, plus
,
variant de 2 ou 3 à 25, caractérisant la technicité de l’entreprise. Plus
la technique est élaborée, plus la valeur des articles est étalée, plus ![]() est élevé.
est élevé.
Bien entendu, il conviendra de tenir compte de cette caractéristique pour effectuer un classement efficace qui aboutira à une gestion sélective, mais pas forcément uniforme, des articles par catégorie.
La plupart des programmes d’informatique effectuent un classement du type ABC, mais souvent plus complexe.
On introduira souvent deux ou trios catégories supplémentaires, telles que:
- les produits ou articles nouveaux, en approvisionnement et en produits finis, dont la valeur de consommation annuelle ne serait pas significative;
- les produits ou articles pour lesquels aucun mouvement n’a été effectué depuis un an ou plus.
Il faudra également tenir compte qu’un article nomenclaturé, classé catégorie C, peut avoir une importance certaine, mÊme si sa valeur est faible.
En revanche, on aura souvent intérÊt à ne pas gérer, au sens comptable du terme, certains articles qui seront placés en libre service et considérés comme consommés des leur achat – ce qui n’empÊchera pas d’en contrôler les sortiers globales au niveau magasin ou atelier.
2.2. LES COUTS DE STOCKS ET L’OPTIMISATION
La gestion selective doit permettre de définir une politique de gestion adaptée à chaque catégorie d’article.
Politique de gestion veut dire:
- choix d’une méthode de réapprovisionnement:
- détermination du niveau de service adapté à la catégorie de produit, compte tenu de la politique commerciale fixée pour cette catégorie;
- corrélativement, fixation du coÛt de rupture, soit dans les reatrds de livraison (pénalités), soit en cas d’arrÊts d’ateliers difficilement tolérables sur les plans économique et psychologique.
Les différentes méthodes de réapprovisionnement sont, en fait, de plus ou moins prÈs rattachées au principe d’optimisation bien connu: la série économique d’approvisionnement ou de la lancement, étable par WILSON. Cette formule constitue un modÈle mathématique simplificateur, dans lequel on suppose que:
- les coÛts sont proportionnels au nombre de piÈces achetées. Il n’y pas de rabais;
- il n’y a pas pénurie (pas de rupture de stock);
- la demande est constante;
- les coÛts de stockage et de commande ou lancement sont définis et constants.
2.2.1. Calcul du coÛt de stockage Cs
En général, on calcule un taux de possession annuel t% par franc de matériel stocké, bien que certains doivent Être apportés si un stockage entraine des frais fixes anormaux.
Les principaux frais comprennent:
- l’intérÊt du capital immobilisé actuellement supérieur à 12 %;
- le magasinage: loyer et entretien des locaux, assurances, manutention, soit environ 6 %;
- les deteriorations par stockage, trÈs variables, de 0 à 10 %;
- les obsolescences: matériel périmé, vieilli, hors de monde.
Les taux retenus doivent Être fixés par les Services Financiers, en liaison avec les Services Technique. Ils variant actuellement de 20 à 35 % suivant les categories d’articles.
2.2.2. CoÛt d’une commande ou d’un lancement CL
Le coÛt d’une commande à l’extérieur s’établit en calculant le total des frais de fonctionnement du Service Achats et du Service Réception Achats, qu’on divise par le nombre total annuel de lignes de commandes (c’est-à-dire un article unique, une quantité, un prix, un délai).
Ce coÛt de commande est variable suivant la nature des commandes passées et la dimension de l’entreprise ou de l’organisme acheteur. Si les discussions techniques et mises au point doivent aboutir à la definition d’un cahier des charges, comme c;est la plupart du temps le cas pour les Services Publics, le coÛt dépasse 1000 F. Le chiffre de 150 F est courant.
Lorsqu’il s’agit d’un lancemnent interne, il faut calculer de mÊme les frais administratifs, en divisant les frais annuels du service ordonnancement par le nombre de lancements effectués.
A ces frais s’ajoutent les coÛts de réglage des différentes machines qui peuvent Être valorisés de différentes façons, suivant que les réglages s’effectuent pendant les heures de travail des ateliers, ce qui est le cas le plus fréquent, et il convient alors de les comptabiliser au taux de section, ou en dehors et on prendra les heures de régleurs majorées des différentes charges.
Il peut y avoir des cas oÙ le lancement d’une fabrication comporte des frais importants de purge ou de nettoyage (fours, en particulier) ou perte de matiÈre au départ en attendant la stabilisation du processus. Dans chaque cas, une analyse économique s’impose, qui déterminera un ordre de grandeur valuable du coÛt de lancement. Celui-ci pourra dépasser plusieurs milliers de francs.
2.2.3. CoÛt d’approvisionnement
Il convient de trouver l’optimum de ce coÛt d’approvisionnement comportant le stockage et la passation des commandes.
Si N est le
nombre annuel des piÈces consommés (achetées) et n la quantité
approvisionnée ou lancée, constante d’aprÈs les hypotheses
simplificatives, le schema ci-dessous montre que le stock moyen est ![]() .
.
Son coÛt
est donc ![]() CS
ou
CS
ou ![]() at (a étant le prix d’une piÈce).
at (a étant le prix d’une piÈce).
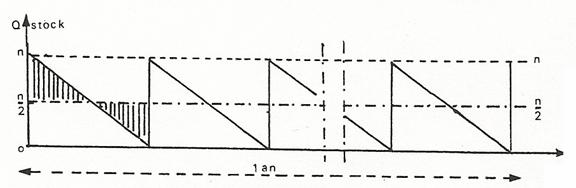
Fig.1. Schéma d’évolution théorique
Le nombre des commandes est ![]() et leur coÛt
et leur coÛt ![]()
Il faut donc trouver n tel que ![]() soit minimum, donc:
soit minimum, donc:
![]() ou -
ou - ![]()
d’oÙ n = 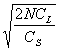 n =
n = ![]()
Cette formule se traduit par un abaque oÙ n apparait en abscisse et N en ordonée. En prenant les logarithmes on a, en effet:
logN = 2Logn +logt – log2![]()
ce qui, en coordonnées
logarithmiques donne un réseau de droites de pente 2 et décalées en fonction
de ![]() .
.
Le coÛt total d’approvisionnement:
C = Na + ![]()
peut s’écrire:
C = Na + ![]()
Au voisinage de l’optimum, le coÛt varie peu. Il n’est donc pas utile de rechercher une valeur exacte de n.
Généralement, suaf
s’il y a des ristournes variables en fonction de la quantité, il vaudra mieux
prendre n de façon à arrondir ![]() à l’entier supérieur.
à l’entier supérieur.
Nous donnons en note technique n0 10 les formules qui peuvent s’appliquer lorsqu’il y a tarif dégressif et lorsqu’on admet une certaine pénurie. Sur un plan pratique on se prémunit du risque de rupture en constituant un stock de sécurité.
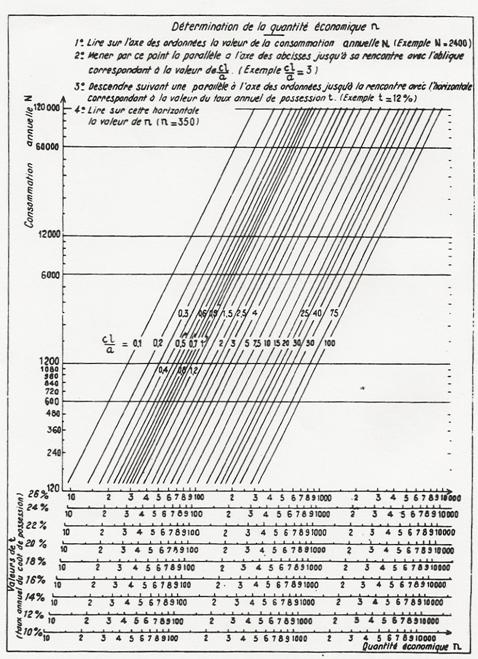
Fig.2. Abaque de série économique
2.3. LE STOCK DE SÉCURITÉ
La demande n’est pas constante mais aléatoire; en dehors mÊme des coefficients saisonniers, elle varie autour d’une moyenne. D’autre part, les délais de livraison sont eux-mÊme variables. Toutefois, les lois de distribution aotour de la moyenne, de la demande et des délais, ne sont pes, en général, de mÊme type. La combinaison de ces deux lois de distribution ne permet donc pas de calculer l’écart type global affectant les deux variables. Dans un premier temps, nous considérerons uniquement les aléas sur la demande.
La valeur moyenne x de la demande est calculée d’aprÈs un historique portant sur un nombre n de périodes dont il faut préciser l’unité: jour, semaine, mois, trimester, etc.
Soit D le délai de livraison en périodes
égales à celles servant de base à l’historique. On peut considérer que la consommation
pendant le délai D est la somme de D variables indépendantes, dont la moyenne
est ![]() et
la variance
et
la variance ![]() .
D’aprÈs les lois statistiques, la demande globale moyenne sera la somme
des moyennes, soit D
.
D’aprÈs les lois statistiques, la demande globale moyenne sera la somme
des moyennes, soit D![]() et la variance sera égale à la
somme des variances.
et la variance sera égale à la
somme des variances.
On aura donc:
![]() et
et ![]()
suivant le risque de rupture admis, le stock de sécurité sera de :
S = t![]()
Si la distribution de la demande est gaussienne et si P le risque de rupture, on aura:
|
P | ||||
|
t |
S’il y a aléas sur le délai, il faut déterminer la loi de
distribution des délais avec une moyenne d et un écart-type ![]() d.
C’est, le plus souvent, une Loi de Poisson.
d.
C’est, le plus souvent, une Loi de Poisson.
Dans certains cas et sous certaines conditions, on peut dire que:
![]()
mais il est preferable, si l’on dispose d’un
ordinateur, de combiner les distributions réelles sur la demande et le délai,
par une simulation suivant la Méthode de
La determination du taux de service doit Être fixée par la Direction.
La notion de « stock 0 » évoquée plus haut concerne évidemment les stocks de security. La poursuite de l’élimination des aléas dus aux transports, aux panes de machines (« 0 pann »), ou aux défauts de fabrication (« 0 défaut ») doit permettre une reduction progressive des stocks de sécurité.
2.4. LES MÉTHODES DE RÉAPPROVISIONNEMENT
Les methods de réapprovisionnement sont indissociables de la gestion des stocks; elles doivent Être adaptées aux différentes categories d’arcticles. D’une façon générale, il faut determiner quelles quantités commander et pour quelle date.
2.4.1. Quantités fixes à dates fixes
C’est, en general, le procédé qu’on peut amployer pour les articles de faible valeur don’t la consummation est réguliÈre. La plupart du temps se seront des articles de la catégorie C; les quantités auront été, à l’origine, estimées par un calcul de série économique. Pour certaines catégories d’articles il peut Être intéressant d’instituer un libre-service – c’est-à-dire que les articles sont supposés consommés lorsqu’ils ont été achetés. Il appartient à chaque responsable de magasin d’en assurer le réapprovisionnement, soit auprÈs d’un magasin central, soit directement auprÈs des fournisseurs.
Certaines entreprises passent, à cet effet, un contrat avec le fournisseur, précisant les caractéristiques techiques et les prix du produit, ainsi qu’une quantité globale annuelle.
Les responsables de magasin eux-mÊme commandent téléphoniquement au fournisseur. Le bordereau de livraison constitue alors la piÈce de base de la facturation; mais le circuit commande administrative est supprimé. La Direction fixe à chaque magasinier un montant mensuel forfaitaire.
2.4.2. Dates fixes et quantités variables. Gestion par calendriers
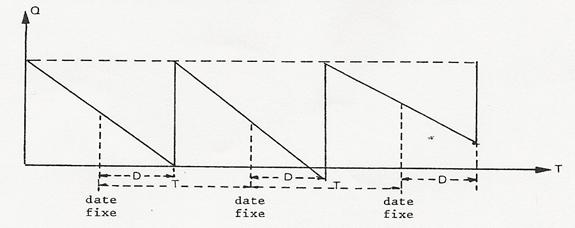
Fig. 3. Approvisionnement sur calendrier
Si T est la période séparant deux commandes, telle qu’elle résulte d’un calcul de série économique, le gestionnaire, fera le point du stock aux dates correspondantes. La réaction à une modification de consommation ne se fera sentir qu’aprÈs le delai de livraison. La période d’incertitude est donc T + d; d’oÙ un stock de sécurité important puisque rapporté à une période souvent longue.
C’est dire que cette méthode s’applique à des produits relativement peu coÛteux, à demande stable.
On répartira les des par catégories: mensuelles, bimestrielles, trimestrielles, semestrielles, etc.
Chaque gestionnaire déterminera, pour chaque jour, les commandes à passer dans chaque catégorie, de façon à répartir son travail ai long de l’année. Il aura donc à dresser un calendrier des commandes, d’oÙ le nom de gestion par calendrier donné à cette méthode.
2.4.3.Quantités fixes et dates variables
Les quantité sont celles résultant du calcul de la série économique. Le gestionnaire suit l’évolution du stock aussi fréquemment que nécessaire.
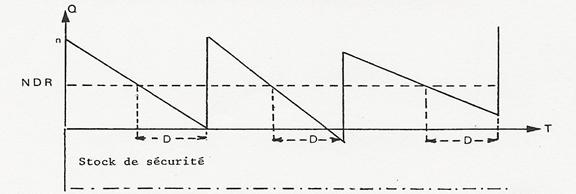
Fig. 4. Approvisionnemnt sur niveau de réapprovisionnement (N.d.R.)
Au délai de livraison correspond une quantité moyenne consommée qui, ajoutée au stock de sécurité, fixe la valeur du « Point de Commande » ou « Niveau de Réapprovisionnement (N.d.R.).
En cas de variations importantes de la consommation, il est nécessaire d’adapter la série économique. Le niveau de réapprovisionnement étant fixé, la quntité Q = Stock de sécurité + N.d.R. peut Être placée dans un magasin, ou tiroirla quantité n – N.d.R. dans un autre. Lorsque ce tiroir est vide, on passe commande, d’oÙ le nom de méthode des deux magasins.
La période d’incertitude est égale au délai de livraison pendant lequel le gestionnaire ne peut intervenir. Le stock de sécurité sera rapporté à ce délai. Il sera plus faible que dans le cas précédent. Par silleurs, le suivi du stock sera continu; sur le plan administratif la méthode sera plus coÛteuse.
La mésera donc, en général, applicable aux articles de la catégorie A.
2.4.4. Quantités variables. Dates variables
Il s’agit de la gestion d’articles coÛteux de la catégorie A dont les prix varient et qui présentent un caractÈre plus ou moins spéculatif: métaux en particulier.
En général, on assurera une gestion graphique en cumuli par période (semaine, quinzaine ou mois) en portent dans chaque période les quantités nécessaire aux différentes commandes (quantités affectées), celles nécessaires aux fabrications pour le stock: on y ajoutera un pourcentage d’aléas. Suivant les conditions du marché on passera les commandes aux prix les plus avantageux.
L’attention demandée par cette méthode ne la rend exploitable que pour un nombre trÈs réduit d’articles: au plus, une dizaine par gestionnaire d’approvisionnement (ou achats).
L’aspect schématique donné aux différentes méthodes ne doit pas dissimuler la souplesse indispensable à l’action, tant du service approvisionnement que du service achats, ainsi que l’importance d’une analyse des coÛts particuliÈre à chaque cas, don’t un exemple est donné ci-dessous.
2.5. NIVEAU ÉCONOMIQUE DU STOCK DE SÉCURITÉ
Nous raisonnerons tout de suite pour fixer les idées sur un exemple précis:
Une usine de fabrication de cable électrique dispose d’un nombre important d’extrudeuses à plastique.
Les vis de ces extrudeuses s’usent assez rapidement et le service entretien en a utilisé, ces dix derniÈres années, une moyenne de 4 par mois.
Si les vis sont commandées 2 mois à l’avance, avec livraison mensuelle, elles coÛtent 8 000 F. Néanmoins, le fournisseur accepte d’en livrer en urgence avec un supplément de 1 000 F. On a relevé l’hirostique suivant des sorties de vos:
|
Quantités mensuelles sorites |
Nombre de mois |
Total sorties |
|
TOTAL.. |
La moyenne mensuelle est de 4.
L’histogramme montre que les sorties suivent approximativement une repartition Poissoienne de moyenne 4.
Le stock normal sera donc de 4. Quel est le stock de sécurité optimum?
Si le taux de possession est de t = 20 %, S le nombre de vis en stock de sécurité et R le nombre de rupture, le coÛt de possession et de rupture sera:
C(S) = S x 8 000 x 0,20 + R x 1 000F
La Table de POISSON, de moyenne 4, donnera la probabilité de ruptures mensuelle, le mois étant la période de base de l’historique. Rapporté à la moyenne 4 et à 11 mois par an, on a le nombre annuel de vis manquantes:
|
Stock de sécurité |
CoÛt du stock |
Probabilités de ruptures |
Nombre annuel de ruptures sur 11 mois |
CoÛt de rupture |
Total C(S) |
|
| |||||
Voir tables des probabilités cumulées. On voit que c’est un stock de sécurité de 3 qui optimise le coÛt du stock de sécurité.
Note technique n0 1
Prévision et coefficients saisonniers
Existence de coefficient saisonnier
Avant de calculer les coefficients saisonnier ou mensuels, il faut verifier leur existence, autrement dit s’assurer, soit par comparaison graphique, soit mieux par un test statistique, qu’il y a correlation entre les ventes et le mois ou la période choisi pour base. On peut employer, par exemple, le test de la correlation linéaire entre les valeurs des ventes du meme mois de deux années différents. On se rapportera au calcul de la droite des moindres carrés exposé dans le chapitre statistique.
Plus rapidement, on peut employer le test de SPEARMANN, décrit en statistique, appliqué au rang des ventes mensuelles pour les deux années considérées.
Le tableau ci-dessous montre que ![]() d2
= 26 (avec d = rang A-4 – rang A-3).
d2
= 26 (avec d = rang A-4 – rang A-3).
Test de Rang de SPEARMANN
|
Ventes A- 4 |
Ventes A- 3 |
Différences des rangs |
||||
|
Quantité |
Rang |
Quantité |
Rang |
d |
d2 |
|
|
Janvier…….. |
24 500 |
2 |
29 500 |
3 |
1 |
1 |
|
Février…….. |
26 000 |
5 |
32 000 |
6 |
1 |
1 |
|
Mars………. |
36 000 |
12 |
36 500 |
10 |
2 |
4 |
|
Avril………. |
27 000 |
7 |
32 500 |
7 |
0 |
0 |
|
Mai……… |
27 500 |
8 |
33 500 |
8 |
0 |
0 |
|
Juin……….. |
29 000 |
10 |
38 000 |
11 |
1 |
1 |
|
Juillet…… |
35 000 |
11 |
35 500 |
9 |
2 |
4 |
|
AoÛt……… |
9 500 |
1 |
6 000 |
1 |
0 |
0 |
|
Septembre… |
25 500 |
4 |
30 500 |
5 |
1 |
1 |
|
Octobre…… |
28 500 |
9 |
39 000 |
12 |
3 |
9 |
|
Novembre… |
26 500 |
6 |
30 000 |
4 |
2 |
4 |
|
Décembre…. |
25 000 |
3 |
28 500 |
2 |
1 |
1 |
Σd2 = 26
Si l’on se réfÈre aux tables ![]() d2
établies pour 12 couples de valeur, on
voit que si:
d2
établies pour 12 couples de valeur, on
voit que si:
![]() d2
d2 ![]() 82,4
82,4
il y a 99 % de chances pour que les ventes soient saisonniÈres.
On porrait, par précaution, établir le mÊme test sur deux autres années de l’historique.
Une fois établie l’existence de la saisonnalité, on procÈde au calcul des coefficients saisonniers.
Dans le tableau figurant au Chap. 4 on prendra respectivement les nombres figurant pour chaque mois dans la colonne Total. On divisera chacun par le Total general des ventes des 4 années. On obtiendra ainsi les coefficients mensuels figurant dans le colonne Coefficients. En multipliant par 100 on obtient les coefficients en % des ventes par mois.
Cette méthode est dite méthode de calcul au Total.
Elle a l’inconvénient, si la tendance est croissante, de minimiser les coefficients de début d’années et de majorer ceux de fin a’année. Aussi préfÈre-t-on souvent la méthode des moyennes mobiles.
2. Méthode de la moyenne mobile
Considérons le mois de Juillet de A-4.
La moyenne mobile pour ce mois sera rapportée à 13 mois.
MjulA-4 = ![]() = 26
875
= 26
875
Par raison de symétrie, les deux mois extrÊmes comptent pour la moitié de leur valeur.
Le coefficient du maois de juillet sera alors:
CA-4jul = ![]() = 1,3
= 1,3
La somme des coefficients ainsi calculés sera de 12.
Un procédé pratique pour calculer les coefficients sera, pour chaque mois, de faire la suite des sommes des 12 mois encadrant ce mois:
S jul = J+F+M+A+M+J+J+A+S+O+N+D
S+1 = F+M+A+M+J+J+A+S+O+N+D+JA-3
On passe rapidement de S à S +1 en supprimant le 1er mois de S et en ajoutant le dernier mois de S +1.
On a alors:
MjulA-4 = ![]()
En effet: ![]()
= ![]()
= ![]()
Ce procédé de la moyenne mobile a l’inconvénient de ne pas permettre le calcul des coefficients des 6 premiers et des 6 derniers mois de la série. Il suppose donc une bonne stabilité de ces coefficients.
S’il y a saisonnalité, on ne peut calculer la tendance qu’aprÈs avoir désiasonnalisé les données, soit par les moyenne sur l’année, soit par les moyennes mobiles.
La modification de tendance sera, par exemple, pour juilletA-1:
Modification M de tendance = Moyenne mobile juA-1
- Moyenne mobile juA-2
ou, en %:
![]()
Un procédé de prévision de la tendance par le calcul consistera à déterminer la droite des moindres carrés entre les moyenne mobiles mensuelles successives, sous réserve que croissance reste linéaire, c’est-à-dire qu’il n;y ait pas de variations brusques de la conjoncture.
Soit Pn la prévision de vente pour un mois n, le mois O étant celui de la 1re moyenne calculée;
Soit a, la coefficient angulaire de la droite des moindres carrés établie à partir de moyennes mobiles de la série;
Soit b l’ordonnée d’origine de cette droite;
Cm le coefficient saisonnier du mois considéré.
On aura:
Pn = (an + b)Cm
Il faudra toujours avoir à l’esprit le fait qu’il s’agit d’un calcul prévisionnel qui devra Être module par les informations reçues directement des différents canaux.
Note techique n0 2
Cas particuliers d’emploi de la sérié économique
Si le fournisser consent des rabais par tranches applicables à la totalité de la commande le schéma devient le suivant.
Si q est la quantité commandée, on aura successivement les rabais suivants:
![]() prix
a rabais r = 0
prix
a rabais r = 0
Q1![]() rabais
r1
rabais
r1
Q2![]() rabais2
rabais2
La courbe du coÛt total d’approvisionnement est formée de plusieurs branches correspondent chacune à la zone de validité du rabais. Il s’agit de trouver le point minimum de cet ensemble de portions de courbes.
De 0 àQ1 C0
= Na + ![]()
De Q1 à Q2 C1 = Na(1-r1)+![]()
De Q2 à Q3 C2 = Na(1-r2)+![]()
De Q3 à Q4 C3 = Na(1-r3)+![]()
En général, les quantités correspondant à la série économique sont trÈs voisines et un seul point de quantité économique se trouvera dans la zone de validité des rabais. Les comparaisons sont donc à faire avec des points qui ne sont pas des valeurs de série économique.
Prenons pour exemple un atelier fabriquant des bagues en acier, cédées à un autre établissement au prix a = 20 F.
N = 20 000 CL = 360 F t = 20 %
Pour 0![]() a = 20 F r = 0
a = 20 F r = 0
1
000![]() r
= 2 %
r
= 2 %
3000![]() r
= 3 % rabais consentis
r
= 3 % rabais consentis
6000![]() r
= 4 %
r
= 4 %
On a n = ![]() = 1 890
= 1 890
avec r = 0
avec r1 = 2 % n1 = 1915
avec r2 = 3 % n2 = 1925
avec r3 = 4 % n3 = 1935
Seule la quantité économique n1 se trouve dans la zone de validité du rabais qui lui est applicable.
On peut tracer le tableau des différents des différents coÛt totaux d’approvisionnement en fonction des quantités commandées. On constate que le minimum est obtenu pour des commandes de 3 000.
Toutefois, si on passe dans l’année un nombre entier de commandes, par exemple 7, alors que le calcul a été fait sur 6,66 commandes, on obtient un chiffre un peu supérieur.
|
Rabais |
Quantité Commandé q |
N X A |
|
|
Total |
Points |
|
Courbe C |
A |
|||||
|
B |
||||||
|
r = 0 |
C |
|||||
|
D |
||||||
|
E |
||||||
|
Courbe C1 |
A1 |
|||||
|
B1 |
||||||
|
rl = 2 % |
C1 |
|||||
|
D1 |
||||||
|
E1 |
||||||
|
Courbe C2 |
A2 |
|||||
|
B2 |
||||||
|
r2 = 3 % |
C2 |
|||||
|
D2 |
||||||
|
E2 |
||||||
|
Courbe C2 |
A3 |
|||||
|
B3 |
||||||
|
r3 = 4 % |
C3 |
|||||
|
D3 |
||||||
|
E3 |
On voit que le point minimum valide est D2 = 396 200
Les différents points sont reportés sur la figure 5.
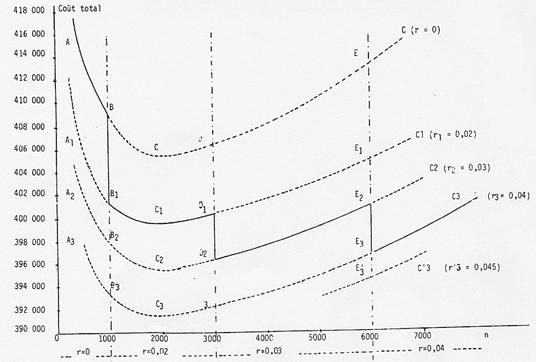
Fig. 5. Courbe des coÛts d’approvisionnement (Tarif dégressif)
Il n’existe pas de définition de coÛt de pénurie. La formulation de ce cas est donc trÈs souvent confuse. On peut dire que le coÛt de pénurie représente l’ ensemble des frais résultant pour l’entreprise du manque en stock d’un article donné pendant une période determine. La pénurie a donc, suivant la nature de l’article, des conséquences plus ou moins graves.
Pénalités pour les livraisons simplement différées.
Perte de clientele pour des ventes manquées.
ArrÊt de machines pour des piÈces d’entretien.
ArrÊt de fabrication pour les matiÈres et piÈces approvisionnées.
Certains frais sont calculables, d’autres ne peuvent Être qu’estimés mais peuvent Être trÈs lourds.
Les coÛt peuvent également Être, soit proportionnels au nombre d’objets et au temps (cas de pénalités), soit liés à chaque rupture (arrÊts d’ateliers). Nous examinerons uniquement le premier cas, le second étant à éviter.
CoÛt de pénurie lié au temps at au nombre d’articles.
Ce coÛt, désigné par Cp est proportionnel au temps et effecté à chaque article manquant.
Soit t1 la durée pendant laquelle le stock est positif et t la période entre deux approvisionnements.
![]() représente le taux de service
représente le taux de service
Pendant t – t1 = t2 il y a rupture de stock
On a le schema suivant (fig. 6)
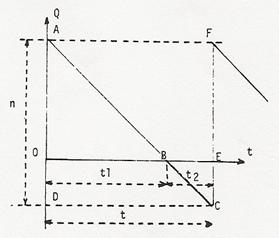
Fig.6. Approvisionnement avec pénurie
![]()
Donc AO = ![]() n
n
Comme t1 = ![]() t
t
Le coÛt du stock reel pendant
un an est: ![]()
On a de meme
EC = AD –AO = n - ![]()
La quantité moyenne en retard de livraison
est donc: ![]()
Le retard étant
de t2 = ![]()
La pénalité de retard sera donc pour l’année de:
(1 - λ)2 ![]()
Le coÛt total d’approvisionnement, fonction de n et de λ, sera donc:
C(n, λ) = Na + ![]() CL
+[λ2CS + (1 - λ)2CP]
CL
+[λ2CS + (1 - λ)2CP]![]()
Le trinôme entre crochets peut s’écrire:
f( ) = λ2(CS + Cp) - 2λCp + Cp avec λ<1
Il
est minimum pour λ =
![]()
La coÛt total minimisé par rapport à sera donc:
C(n, ) = Na + ![]()
![]()
C(n, λ) = Na + ![]()
On a, au facteur λ prÈs, la mÊme expression que pour la série économique simplifiée qui deviendra:
n = 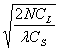
Cette formule a un intérÊt plus théorique que pratique; il est préférable de traiter cette question sous son aspect probabiliste, c’est-à-dire par le stock de sécurité.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2587
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved