| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
Fonctions Logiques - Combinatoire
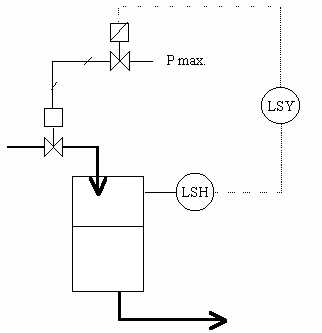
Le capteur LSH est un détecteur de seuil pouvant délivrer un contact ouvert au repos (normalement ouvert) ou un contact fermé au repos (normalement fermé). L'organe de correction est une vanne pneumatique fonctionnant sur du 0 de pression (pression atmosphérique) ou une pression maximale en général comprise entre 4 et 10 bar relatifs. La commande pneumatique est admise dans le servomoteur de la vanne procédé au moyen d'une électrovanne sur le circuit pression appareil. Cette électrovanne de commande fonctionne en général en 24 V continu.
LSY est un automate programmable ou simplement un pilote électronique, son rôle est d'assurer la loi de commande.
Cablages :
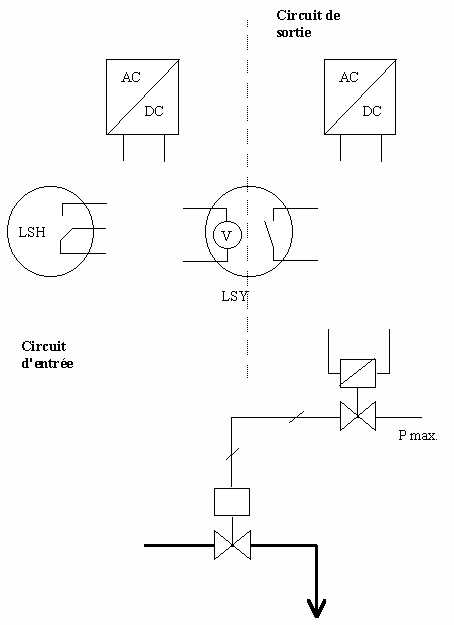
Le transformateur redresseur n'est présent que lorsque l'automate LSY présente des contacts secs en entrée et en sortie. L'automate peut lui-même alimenter le circuit d'entrée et le circuit de sortie. L'entrée du LSY fonctionne comme un voltmètre, en fait le LSY détecte la continuité électrique dans le circuit d'entrée et assure ou non (contact) la continuité électrique dans le circuit de sortie.
On constate qu'un premier choix doit être fait : sur le détecteur, il faut choisir un contact NO ou NF, sur l'électrovanne de commande, il faut choisir une électrovanne NO ou NF et sur la vanne de commande procédé, il faut choisir une vanne NO ou NF.
La sécurité du procédé est assurée par la vanne pneumatique, dans notre cas, la sécurité du procédé impose une vanne NF (éviter le débordement du réservoir en cas de problème) ; cette position correspond à un défaut de pression dans le servomoteur de la vanne pneumatique. La position de repos de la vanne pneumatique doit correspondre à la position de repos de l'électrovanne, ainsi, en cas de coupure du circuit de commande de l'électrovanne, celle-ci prend sa position de repos, coupant la pression dans le servomoteur de la vanne pneumatique pour que celle-ci rejoigne sa position de repos et donc sa position de sécurité. La pression d'air devant être toujours coupée, il conviendra de choisir toujours une électrovanne NF.
Enfin, le choix au niveau du détecteur doit faire correspondre une rupture du circuit d'entrée (discontinuité électrique) à la position de repos de la vanne procédé : vanne procédé au repos (fermée) quand le niveau haut est atteint (capteur actif). Donc, lorsque le capteur est actif, le contact est ouvert pour assurer la discontinuité électrique ; au repos, le capteur doit être fermé. Il convient donc de choisir un capteur NF.
Cablage :
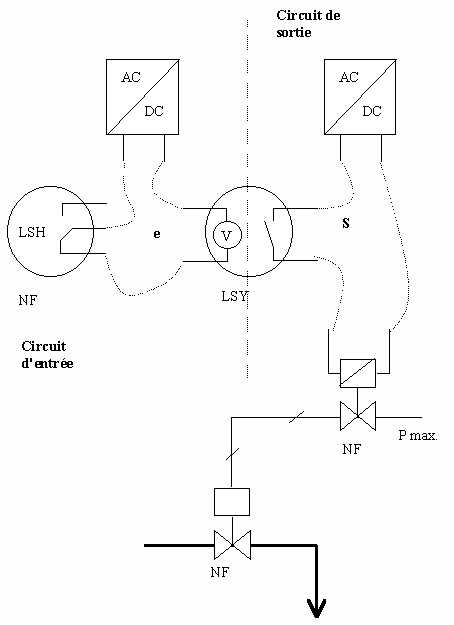
Loi de commande :
Elle résulte de la proposition logique suivante : 'Si le niveau haut est atteint alors fermer la vanne.'. Cette proposition doit être traduite en terme de continuité électrique des circuits d'entrée et de sortie puisque l'automate détecte la continuité électrique du circuit d'entrée et assure celle du circuit de sortie.
Cette proposition est modifiée de la façon suivante :
Niveau haut atteint Capteur actif Contact ouvert (NF) Discontinuité électrique du circuit d'entrée.
Vanne procédé fermée Pression du servomoteur nulle (NF) Electrovanne fermée Servomoteur hors tension (NF) Discontinuité électrique du circuit de sortie.
Nous avons alors : 'Si Discontinuité électrique du circuit d'entrée alors Discontinuité électrique du circuit de sortie.'
Le capteur est cablé sur l'entrée e du LSY et la vanne est cablée sur la sortie s du LSY.
Conventions :
Lorsque une entrée ou une sortie digitale (2 positions) est en état de continuité électrique, elle est prise à 1, lorsqu'elle est en état de discontinuité électrique, elle est prise à 0.
La loi de commande s'écrit alors : 'Si e=0 alors S=0' ou encore plus simplement :
S = e
Il s'agit de la fonction logique Identité.
Remarque : on peut vérifier que cette fonction logique assure le complémentaire de la proposition donnée au départ : 'Si le niveau haut n'est pas atteint alors ouvrir la vanne.'.
II. Variables Booléennes et Fonctions Logiques :
Une variable booléenne est une variable qui ne peut prendre que deux valeurs discrètes que l'on nomme 0 ou 1.
Une fonction logique est une combinaison donnée des variables d'entrées.
Lorsque l'on réalise une combinaison de n variables d'entrées, on peut obtenir 2n combinaisons différentes.
Nous avons déjà vu la fonction identité, la fonction complément défini le contraire de l'identité. Il existe 2 autres fonctions logiques de base, le ET et le OU, puis 4 fonctions particulières méritant d'être citées.
II.1. Fonction Identité :
L est une sortie, a et b des entrées.
Proposition logique : 'L est à 1 quand a=1'
Table de Vérité :
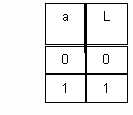
Forme algébrique : L=a
Forme schématique :
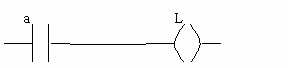
Cette notation vient de la technologie cablée, elle est appelée 'ladder' ou 'langage à contact'. L'équation combinatoire précédante peut être lue de la façon suivante : 'Tant que l'entrée a est à 1, la sortie L est maintenue à 1.' Et aussi : 'Dès que l'entrée a retourne à 0, la sortie L est repositionnée à 0.' La bobine L est excitée tant que le contact est maintenu à 1.
Noter la différence avec la proposition suivante : 'Dès que l'entrée a passe à 1, la sortie L est positionnée à 1.' Et y demeure même si a retourne à 0. Ceci correspond à un 'set' :
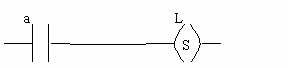
Seul un 'reset' peut ramener à 0 une sortie positionnée à 1 par un 'set'. Par exemple, retour à zéro de L sur passage à 1 du contact b :
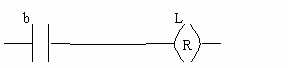
II.2. Fonction Complément :
Proposition logique : 'L est à 1 quand a=0'
Table de Vérité :
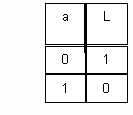
Forme algébrique :
![]()
Forme schématique :
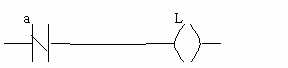
II.3. Fonction ET :
Proposition logique : 'L est à 1 quand a=1 et b=1'
Table de Karnaugh :
la présentation en table de vérité est toujours valable mais jusqu'à 4 variables d'entrées, la table de Karnaugh permet la simplification rapide des fonctions logiques ; cette présentation sera donc préférée à la table de vérité.
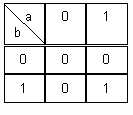
Forme algébrique : L=a.b
Forme schématique :
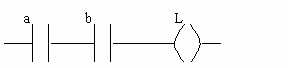
II.4. Fonction OU :
Proposition logique : 'L est à 1 quand a=1 ou b=1'
Table de Karnaugh :
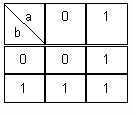
Forme algébrique : L=a+b
Forme schématique :
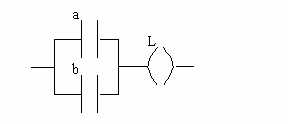
II.5. Fonction NON ET (Nand) :
Proposition logique : Proposition complémentaire de ET
Table de Karnaugh : Complémentaire.
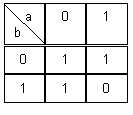
Forme algébrique :
![]()
(Théorème de Morgan : § III.1)
Forme schématique :
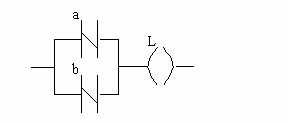
II.6. Fonction NON OU (Nor) :
Proposition logique : Proposition complémentaire du OU
Table de Karnaugh : Complément

Forme algébrique :
![]()
(Théorème de Morgan : § III.1)
Forme schématique :
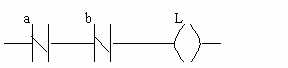
II.7. Fonction OU EXCLUSIF :
Table de Karnaugh :
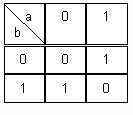
Forme algébrique :
![]()
Cette forme algébrique s'appelle la première forme canonique. Elle s'obtient en exprimant toutes les combinaisons rendant vraie la fonction décrite dans la table.
Dans notre cas : 'L=1 si a=0 et b=1 ou si a=1 et b=0'
Forme schématique :
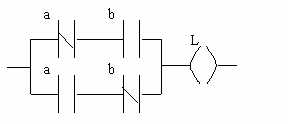
II.8. Fonction COINCIDENCE :
Table de Karnaugh :
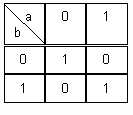
Forme algébrique :
![]()
Forme schématique :
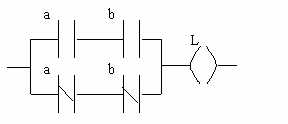
III. Simplification des fonctions logiques :
On obtient la première forme canonique d'une fonction logique à partir de l'expression de toutes les combinaisons des entrées qui rendent vraies la fonction. Cette forme est toujours la plus coûteuse. Le coût évalue le nombre de fonctions ET et OU intervenant dans l'expression.
Par exemple : pour la fonction coïncidence ci-dessus, le coût est de 3.
Pour réduire ce coût, on va procéder à une simplification de la fonction, lorsque celle-ci est possible.
Cette simplification peut se faire par une méthode algébrique prenant en compte les postulats et théorèmes de l'algèbre de Boole ou par une méthode graphique appelée Méthode de Karnaugh.
III.1. Postulats et théorèmes de l'algèbre de Boole :
|
Opérations sur la même variable : |
|
|
Commutativité : |
|
|
Associativité : |
|
|
Distributivité : |
|
|
Eléments neutres : |
|
|
Eléments absorbants : |
|
|
Complémentarité : |
|
|
| |
|
Loi d'involution : |
|
|
Théorème de Morgan : |
|
|
Absorption du multiple : |
|
|
Absorption du complément : |
|
III.2. Méthode de Karnaugh :
Cette méthode utilise la table de Karnaugh. Attention dans la table de Karnaugh lorsque l'on passe d'une case à une case voisine, il ne doit y avoir qu'un seul bit qui change : on appelle cette propriété la propriété d'adjacence.
La méthode de Karnaugh consiste à effectuer des regroupement de cases à 1 par puissance de 2 les plus grandes possibles.
Exemple : soit une fonction à 3 entrées a, b et c. La table comporte 8 cases soit 2 à la puissance 3.
On peut faire un paquet de 8 :
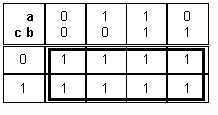
L=1
On peut faire un paquet de 4 :
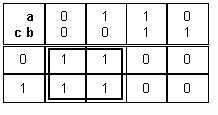
|
On voit que L est à 1 quelque soit la valeur de a et de c pour b=0, donc |
|
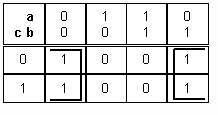
|
On voit que L est à 1 quelque soit la valeur de b et de c pour a=0, donc |
|
On peut faire un paquet de 2 :
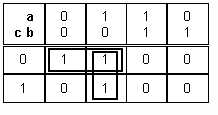
|
On a |
|
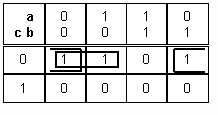
|
On a |
|
On ne peut faire qu'un paquet de 1 ( 2 à la puissance 0) :
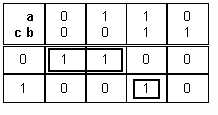
|
On a |
|
Généralisation : Soit une fonction à n entrées, :
Les paquets de 2n
donnent une réduction à L=1
Les paquets de 2n-1 donnent une expression en fonction d'une seule
entrée
Les paquets de 2n-2 donnent une expression en fonction de deux
entrées
…
Les paquets de 21 donnent une expression en fonction de n-1 entrées
Les paquets de 20 donnent une expression en fonction des n entrées
(Première forme canonique).
III.3. Utilisation des combinaisons physiquement impossibles :
Il arrive que certaines combinaisons des entrées soient physiquement impossibles, par exemple sur un réservoir, on positionne un détecteur de niveau haut LSH et un détecteur de niveau bas LSL, on suppose que le capteur est au repos quand le seuil n'est pas atteint.
La combinaison LSL =1 et LSH=1 est physiquement impossible !
Puisque ces combinaisons d'entrées ne se produiront jamais, on peut leur affecter la valeur 1 si cela nous permet de réduire le coût de la fonction.
Exemple :
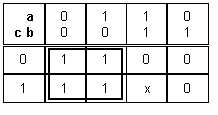
La combinaison a.b.c est impossible mais ne nous permet pas de simplifier davantage la fonction, on l'affecte donc à 0.
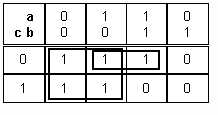
|
Cette fonction se simplifie |
|
|
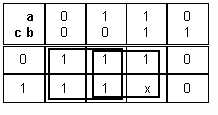
Si maintenant a.b.c est une combinaison impossible alors au lieu d'un paquet de 2, on peut faire un paquet de 4 et la fonction se simplifie davantage : |
|
L'utilisation de combinaisons impossibles dans une méthode de simplification algébrique n'est pas aussi simple que dans la méthode de karnaugh.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1025
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved