| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
|
|
Le dioptre sphérique est la surface sphérique de séparation entre deux milieux optiques.
Soit un point lumineux A placé devant un dioptre sphérique, sur l'axe de symétrie.
On considére un systÈme d'axes de coordonnées xOy ainsi que:
Þ l'axe Ox a la direction qui unit le point A avec le centre du dioptre
Þ l'origine du systÈme d'axes est située dans le sommet du dioptre
Soit un rayon lumineux issu du point A, qui passe par le point I et entrecroise de nouveau l'axe Ox dans le point B. On va déterminer la position du B ainsi que, conformément au principe de Fermat, la durée de propagation est minimum. Pour le rayon qui passe par I la durée de propagation est
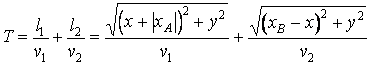
Il y a aussi une relation qui montre que le point I est situé sur un cercle (la section du dioptre) centré en C, de rayon R
![]()
Soit un autre point I' placé sur le dioptre, à petite distance du point I. Si le rayon lumineux parcourait la route AI'B on pourrait écrire
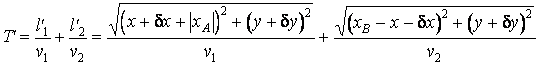
![]()
En considérant dx dy << xA , xB, y, on peut faire les approximations suivantes



Utilisant le principe de Fermat, on obtient
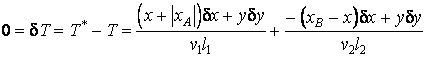
ou

Le rapport dx dy est arbitraire, ce qui implique

ou
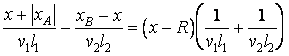
Quand on satisfait à l'approximation
![]()
nommée approximation des rayons paraaxiales ou approximation gaussienne, il résulte
![]()
Dans ce cas, on obtient
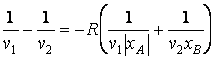
|
|
ou
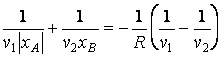
En tenant compte que½xA½= -xA, v1 = c/n1 et v2 = c/n2, il résulte
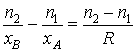
Cette relation est nommée l'équation des points conjugués du dioptre sphérique ou l'équation fondamentale du dioptre sphérique. Elle montre qu'il n'y a pas d'importance quelle direction prendra le rayon issu du point A, car, aprÈs le passage à travers le dioptre, il passera par le point B. Autrement dit, on peut affirmer que tous rayons partis du point A, et qui traversent le dioptre, se rejoindront dans le point B (naturellement, si l'approximation gaussienne est vérifiée), ce qui signifie que B est l'image du A à travers le dioptre.
Quand le point lumineux A occupe une certaine position Fo, de coordonnée
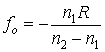
il résulte 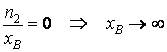 ,
c'est-à-dire les rayons émergents sont parallÈles entre eux (ils
se rencontrent à l'infini). Le point placé dans cette position s'appelle
foyer objet, et sa coordonnée fo s'appelle distance focale objet.
,
c'est-à-dire les rayons émergents sont parallÈles entre eux (ils
se rencontrent à l'infini). Le point placé dans cette position s'appelle
foyer objet, et sa coordonnée fo s'appelle distance focale objet.
D'autre part, un faisceau des rayons de lumiÈre parallÈles (xA ¥) sera concentré dans un point de coordonnée fi
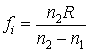
Ce point s'appelle foyer image, et sa coordonnée s'appelle distance focale image.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 684
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved